【实战】葡萄酒质量数据分析

出自《Python数据分析基础》第7章 描述性统计与建模
使用统计图和摘要统计量对数据集进行探索和摘要分析，以及如何使用多元线性回归和逻辑斯蒂回归进行回归和分类分析。

一、环境

完成这种类型的任务使用Jupyter比较方便。

1. 安装Jupyter

需要有Python环境。
在CMD中：

pip install notebook

2. 运行

在CMD中：

jupyter notebook

会自动打开浏览器的jupyter页面。
新建 winequality.ipynb，作为本次分析的报告。

3. 库

这里需要用到如下几个库。
numpy
pandas
seaborn
matplotlib
statsmodels

没有的库需要自己pip安装。这里演示安装statsmodels库。

二、数据集

红葡萄酒：https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv
白葡萄酒：https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv

将数据保存为CSV后缀文件，直接使用excel打开，可能不能正确显示（如下图所示）。
原因是该 CSV 文件使用 分号（;）作为列分隔符，但 Excel 默认使用 逗号（,）或 制表符（Tab）作为分隔符。因此，Excel 会将整行数据视为一个单元格，导致格式错乱。

可以使用excel的导入功能。

将原数据保存为txt，导入。

自己手动加了一列type，标识酒的类型。

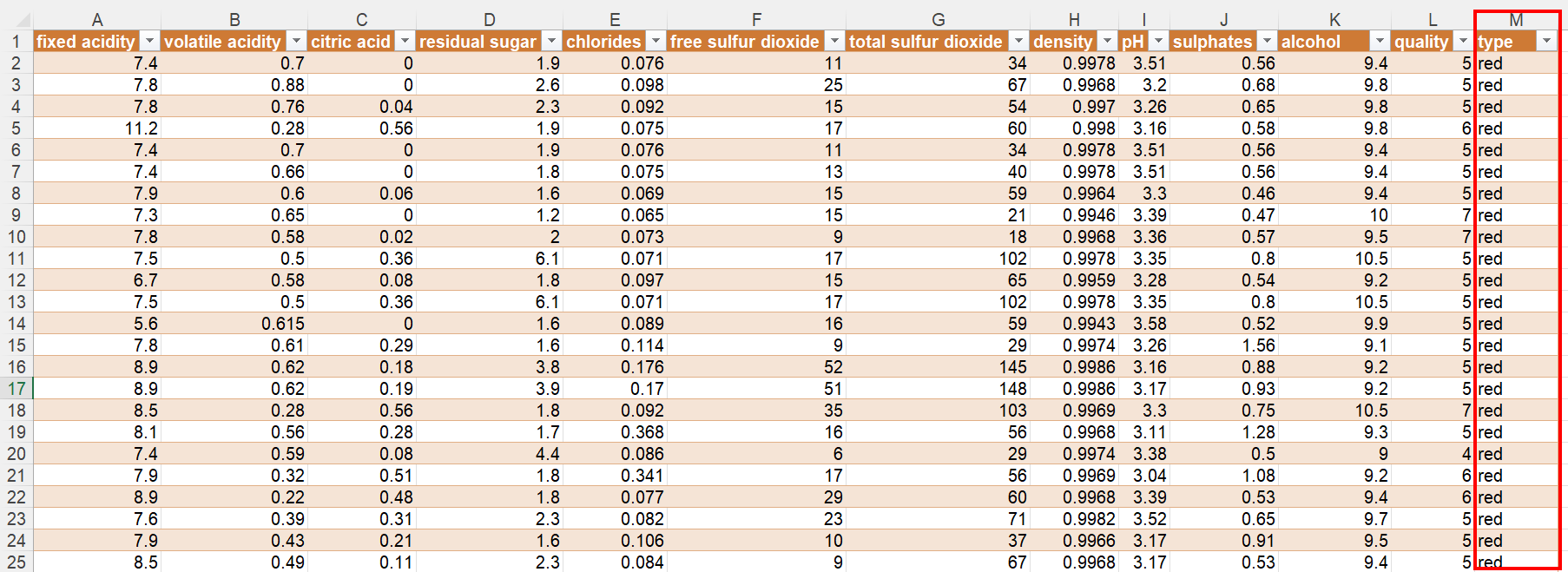
同样的方法导入另一种酒的数据，将数据复制到一起。

把csv文件上传到工程目录下。

三、葡萄酒质量

1. 描述性统计

导入库

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.formula.api import ols, glm

将数据集读入到pandas数据框中

有些列标题中包含空格（例如：fixed acidity），要使用下划线替换空格。这一步操作是为了让列名更 “友好”，避免后续写代码时频繁处理特殊字符带来的麻烦，属于数据分析中的常规预处理习惯
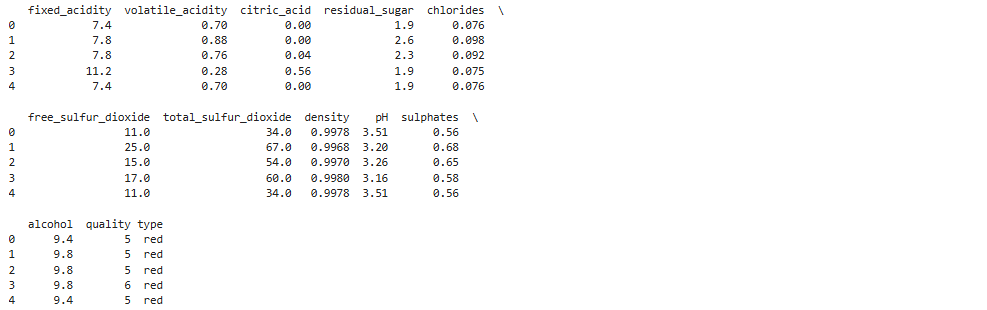
使用head函数检查一下标题行和前5行数据，确保数据被正确加载。

wine = pd.read_csv('winequality-both.csv', sep=',', header=0)
wine.columns = wine.columns.str.replace(' ', '_')
print(wine.head())

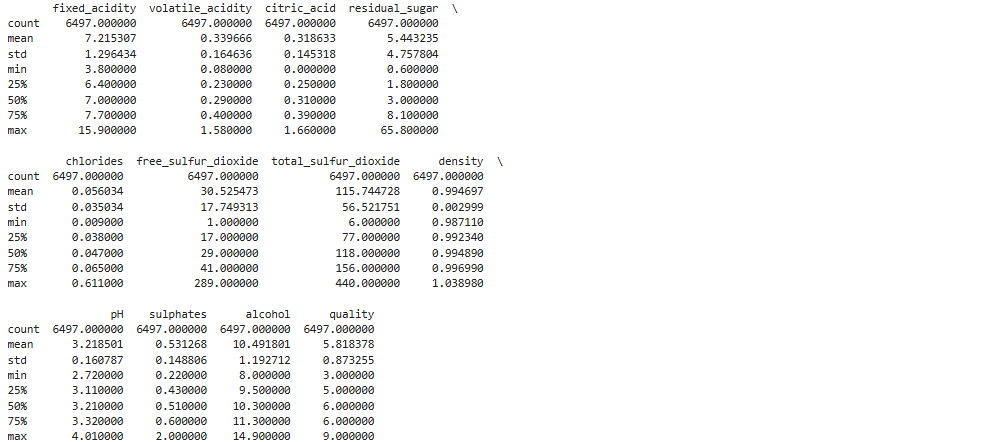
显示所有变量的描述性统计量

包括总数、均值、标准差、最小值、第25个百分位数、中位数、第75个百分位数和最大值。

print(wine.describe())

找出质量列中的唯一值，并以升序打印在屏幕上

print(sorted(wine.quality.unique()))

计算值的频率

print(wine.quality.value_counts())

2. 分组、直方图与t检验

分别分析红葡萄酒和白葡萄酒

# 数据筛选 ===================================
# 按照葡萄酒类型查看质量分布======================
red_wine = wine.loc[wine['type']=='red', 'quality']
white_wine = wine.loc[wine['type']=='white', 'quality']

# 可视化设置与绘图 直方图：展示数据的分布情况=======
sns.set_style("dark")
sns.histplot(red_wine, stat="density", kde=False, color="red", label="Red wine", bins=[2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5])
sns.histplot(white_wine, stat="density", kde=False, color="lightblue", label="White wine", bins=[2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5])

# 图表美化与展示 ================================
plt.xlabel("Quality Score")
plt.ylabel("Density")
plt.title("Distribution of Quality by Wine Type")
plt.legend()
plt.show()

sns.histplot()：seaborn 的直方图函数，用于展示数据的分布情况。

• stat="density"：纵轴表示 “密度”（即频率 / 组距，使直方图总面积为 1，便于不同样本量的分布对比）。
• kde=False：不显示核密度曲线（仅保留直方图）。
• color：指定直方图颜色（红葡萄酒用红色，白葡萄酒用浅蓝色，符合直观认知）。
• label：为图例设置标签，用于区分两种葡萄酒。

手动定义分箱边界
bins = [2.5, 3.5, 4.5, ..., 9.5] 确保每个区间（如[3.5,4.5)）的中心正好是整数（如 4），柱子会对齐到中心位置。

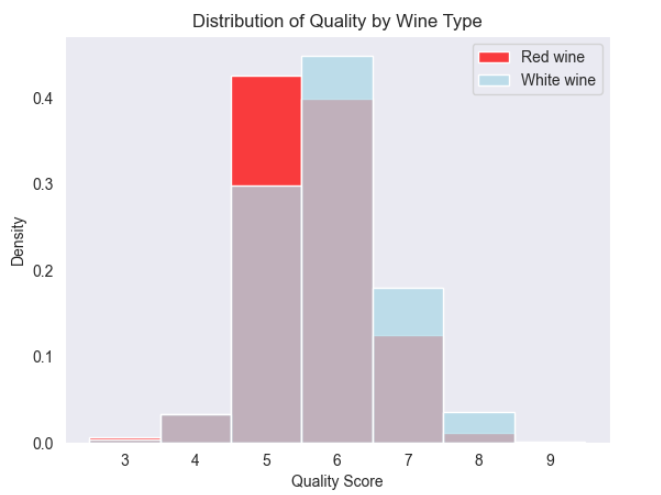
因为白葡萄酒数据比红葡萄酒多得多，所以图中显示密度分布，不显示频率分布。
从图可以看出，两种葡萄酒的评分都近似正态分布。
与原始数据的摘要统计量相比，直方图更容易看出两种葡萄酒的质量评分的分布。

t检验

判断红葡萄酒和白葡萄酒的平均评分是否有区别

print(wine.groupby(['type'])[['quality']].agg(['std']))
tstat, pvalue, df = sm.stats.ttest_ind(red_wine, white_wine)
print('tstat: %.3f pvalue: %.4f' % (tstat, pvalue))

在本例中，我们想知道红葡萄酒和白葡萄酒评分的标准差是否相同，所以在t检验中可以使用合并方差。
t检验统计量为-9.69，p值为0.00，这说明白葡萄酒的平均质量评分在统计意义上大于红葡萄酒的平均质量评分。

3. 成对变量之间的关系和相关性

计算所有数值型变量的相关矩阵

numeric_wine = wine.select_dtypes(include=['number'])
print("数值型变量的相关矩阵：")
print(numeric_wine.corr())

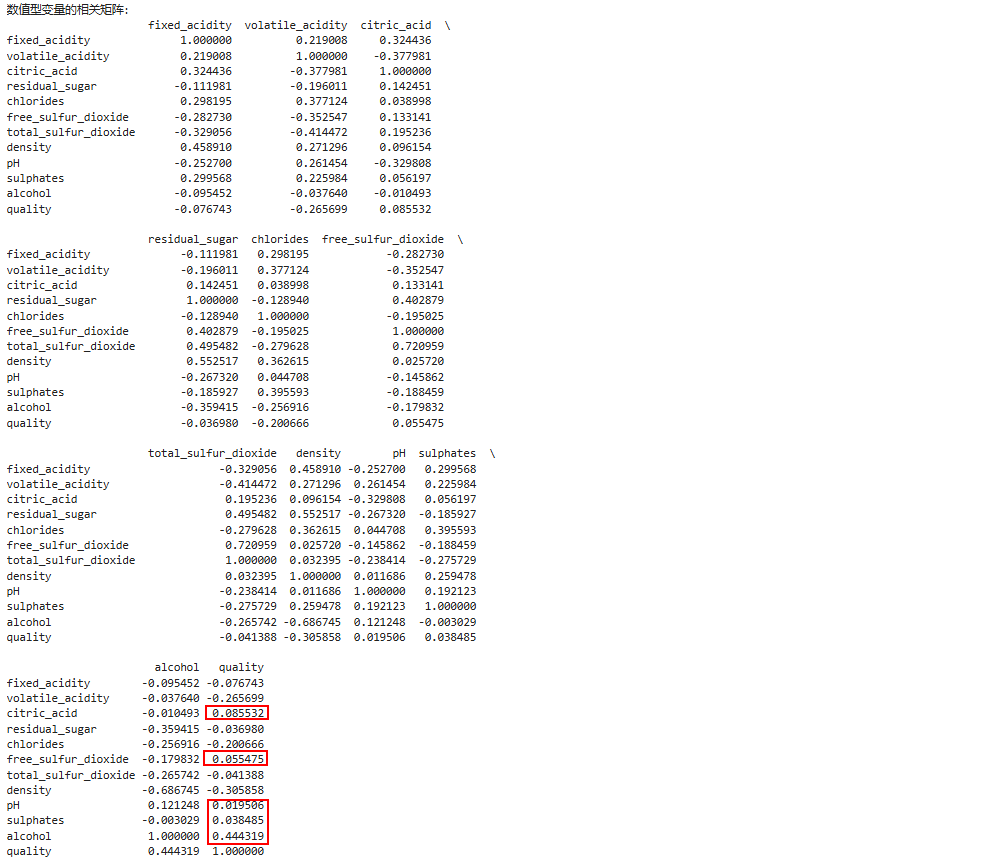
从输出中可以知道酒精含量、硫酸盐、pH 值、游离二氧化硫和柠檬酸这些指标与质量是正相关的，
非挥发性酸、挥发性酸、残余糖分、氯化物、总二氧化硫和密度这些指标与质量是负相关的。

从红葡萄酒和白葡萄酒的数据中取出一个“小”样本（用于绘图）

数据集中有6000 多个点，所以如果将它们都画在统计图中，就很难分辨出清楚的点。
为解决这个问题，定义了一个函数take_sample，用来抽取在统计图中使用的样本点。

def take_sample(data_frame, replace=False, n=200):
    return data_frame.loc[np.random.choice(data_frame.index, replace=replace, size=n)]
reds_sample = take_sample(wine.loc[wine['type']=='red', :])
whites_sample = take_sample(wine.loc[wine['type']=='white', :])
wine_sample = pd.concat([reds_sample, whites_sample])
wine['in_sample'] = np.where(wine.index.isin(wine_sample.index), 1.,0.)
print(pd.crosstab(wine.in_sample, wine.type, margins=True))

查看成对变量之间的关系

创建一个统计图矩阵。
主对角线上的图以直方图或密度图的形式显示了每个变量的单变量分布，
对角线之外的图以散点图的形式显示了每两个变量之间的双变量分布，
散点图中可以有回归直线，也可以没有。

# 查看成对变量之间的关系
sns.set_style("dark")
g = sns.pairplot(
    wine_sample, 
    kind='reg', 
    plot_kws={"ci": False, "x_jitter": 0.25, "y_jitter": 0.25}, 
    hue='type', 
    diag_kind='hist',
    diag_kws={"bins": 10, "alpha": 0.3}, 
    palette=dict(red="red", white="green"),
    markers=["o", "x"], 
    vars=['quality', 'alcohol', 'residual_sugar']
)
print(g)
plt.suptitle(
    'Histograms and Scatter Plots of Quality, Alcohol, and Residual Sugar', 
    fontsize=14, 
    horizontalalignment='center', 
    verticalalignment='top',
    x=0.5, 
    y=1
)
plt.show()

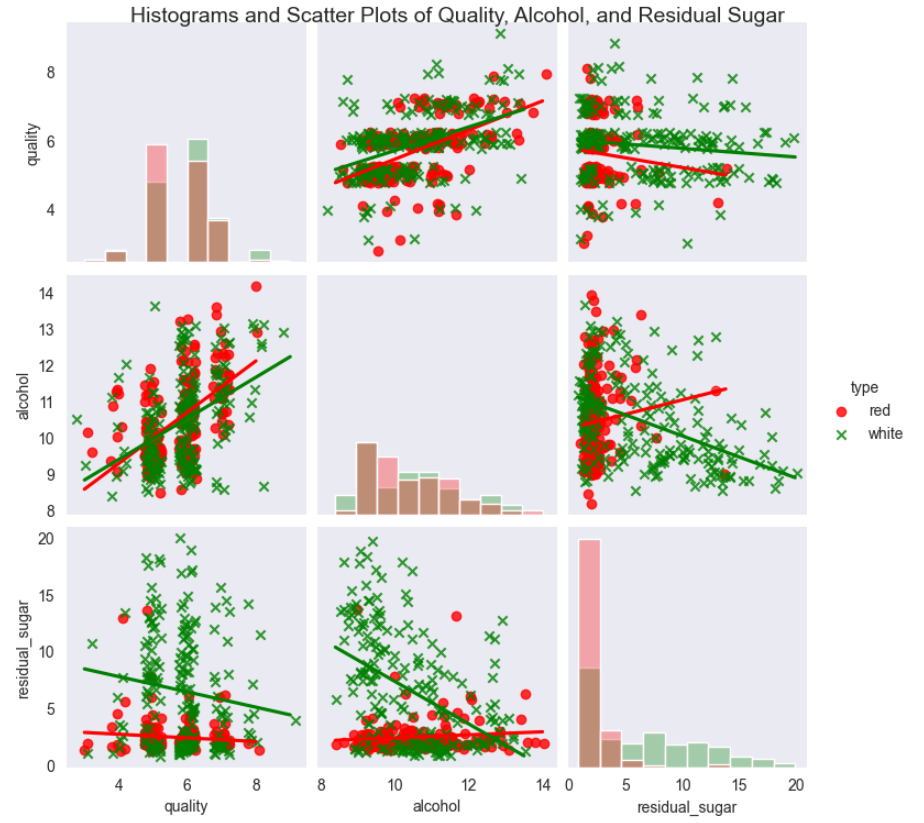
上图显示了葡萄酒质量、酒精含量和残余糖分之间的关系。
红条和红点表示红葡萄酒，白条和白点表示白葡萄酒。
因为质量评分都是整数，所以加上了一点振动，这样更容易看出数据在何处集中。
从这些统计图可以看出，对于红葡萄酒和白葡萄酒来说，酒精含量的均值和标准差是大致相同的，
但是，白葡萄酒残余糖分的均值和标准差却大于红葡萄酒残余糖分的均值和标准差。
从回归直线可以看出，对于两种类型的葡萄酒，酒精含量增加时，质量评分也随之提高，
相反，残余糖分增加时，质量评分则随之降低。

4. 使用最小二乘估计进行线性回归

相关系数和两两变量之间的统计图有助于对两个变量之间的关系进行量化和可视化，
但是它们不能测量出每个自变量在其他自变量不变时与因变量之间的关系。
线性回归可以解决这个问题。

my_formula = 'quality ~ alcohol + chlorides + citric_acid + density\
+ fixed_acidity + free_sulfur_dioxide + pH + residual_sugar + sulphates\
+ total_sulfur_dioxide + volatile_acidity'
lm = ols(my_formula, data=wine).fit()
## 或者，也可以使用广义线性模型（glm）语法进行线性回归
## lm = glm(my_formula, data=wine, family=sm.families.Gaussian()).fit()
print(lm.summary())
print("\nQuantities you can extract from the result:\n%s" % dir(lm))
print("\nCoefficients:\n%s" % lm.params)
print("\nCoefficient Std Errors:\n%s" % lm.bse)
print("\nAdj. R-squared:\n%.2f" % lm.rsquared_adj)
print("\nF-statistic: %.1f P-value: %.2f" % (lm.fvalue, lm.f_pvalue))
print("\nNumber of obs: %d Number of fitted values: %d" % (lm.nobs,\
len(lm.fittedvalues)))

5. 系数解释

如果你想使用这个模型弄清楚因变量（葡萄酒质量）和自变量（11 个葡萄酒特性）之间的关系，就应该解释一下模型系数的意义。
在这个模型中，某个自变量系数的意义是，在其他自变量保持不变的情况下，这个自变量发生1个单位的变化时，导致葡萄酒质量评分发生的平均变化。
例如，酒精含量系数的含义就是，从平均意义上来说，如果两种葡萄酒其他自变量的值都相同，那么酒精含量高1个单位的葡萄酒的质量评分就要比另一种葡萄酒的质量评分高出0.27分。
并不是所有的系数都需要解释。
例如，截距系数的意义是当所有自变量的值都为 0 时的期望评分。因为没有任何一种葡萄酒的各种成分都为0，所以截距系数没有具体意义。

6. 自变量标准化

关于这个模型，还需要注意的一点是，普通最小二乘回归是通过使残差平方和最小化来估计未知的 β 参数值的，这里的残差是指自变量观测值与拟合值之间的差别。
因为残差大小是依赖于自变量的测量单位的，所以如果自变量的测量单位相差很大的话，那么将自变量标准化后，就可以更容易对模型进行解释了。
对自变量进行标准化的方法: 先从自变量的每个观测值中减去均值，然后再除以这个自变量的标准差。自变量标准化完成以后，它的均值为0，标准差为1.
可以对一个观测写一个变换公式，pandas可以把这个公式扩展到行与列中，来标准化所有变量。

# 创建一个名为dependent_variable的序列来保存质量数据
dependent_variable = wine['quality']
# 创建一个名为independent variables的数据框
# 来保存初始的葡萄酒数据集中除quality、type和in_sample之外的所有变量
independent_variables = wine[wine.columns.difference(['quality', 'type', 'in_sample'])]
# 对自变量进行标准化
# 对每个变量，在每个观测中减去变量的均值
# 并且使用结果除以变量的标准差
independent_variables_standardized = (independent_variables - independent_variables.mean()) / independent_variables.std()
# 将因变量quality作为一列添加到自变量数据框中
# 创建一个带有标准化自变量的
# 新数据集
wine_standardized = pd.concat([dependent_variable, independent_variables_standardized], axis=1)
# 重新进行线性回归，并查看一下摘要统计
lm_standardized = ols(my_formula, data=wine_standardized).fit()
print(lm_standardized.summary())

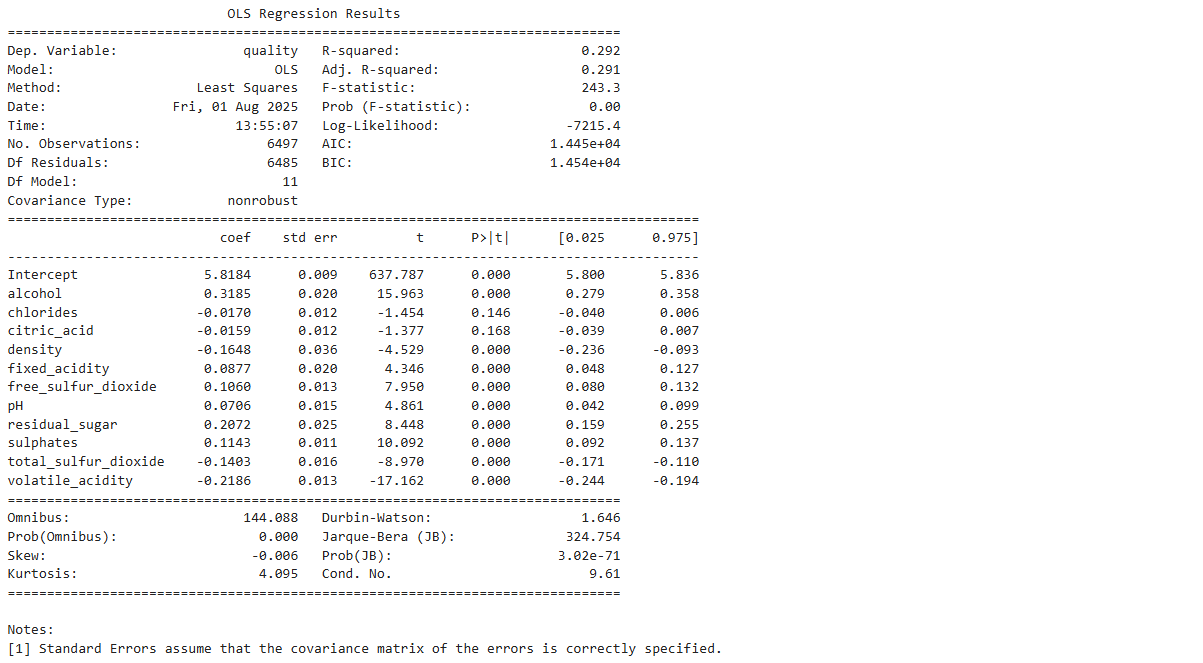
自变量标准化会改变我们对模型系数的解释。
现在每个自变量系数的含义是，不同的葡萄酒在其他自变量均相同的情况下，某个自变量相差1个标准差，会使葡萄酒的质量评分平均相差多少个标准差。
举个例子，酒精含量系数的意义是，从平均意义上说，如果两种葡萄酒其他自变量的值都相同，那么酒精含量高1 个标准差的葡萄酒的质量评分就要比另一种葡萄酒的质量评分高出0.32个标准差。
自变量标准化同样会改变我们对截距的解释。
当解释变量被标准化后，截距表示的就是当所有自变量取值为均值时因变量的均值。
在我们的模型摘要中，截距系数的意义就是当一种葡萄酒所有的成分都取均值的时候，它的质量评分均值应该是5.8，标准差为0.009。

7. 预测

仅出于方便和演示的目的，才使用这些已经用于拟合模型的数据。
除了这个示例之外，你应该使用未用于拟合模型的数据来评价模型，并用新的观测数据进行预测。

# 使用葡萄酒数据集中的前10个观测创建10个“新”观测
# 新观测中只包含模型中使用的自变量
new_observations = wine.loc[wine.index.isin(range(10)), independent_variables.columns]

# 基于新观测中的葡萄酒特性预测质量评分
y_predicted = lm.predict(new_observations)

# 将预测值保留两位小数并打印到屏幕上
y_predicted_rounded = [round(score, 2) for score in y_predicted]
print(y_predicted_rounded)

技巧总结

1. 密度分布与频率分布

	频率分布（Frequency Distribution）	密度分布（Density Distribution）
计算方式	直接统计每个区间内的数据数量（或占比）	对频率分布进行归一化处理，使分布的总面积（积分）为 1
数值含义	纵轴表示：计数（count）：区间内的样本数量；频率（proportion）：区间内样本占总样本的比例	纵轴表示：单位区间内的概率密度（概率 / 区间宽度），本身不直接等于概率
总面积 / 总和	计数总和 = 总样本量；频率总和 = 1	曲线下总面积 = 1（满足概率密度的性质）

频率分布：

• 适合直观展示 “每个区间有多少数据”，便于比较不同组的样本数量差异。
• 例如：比较两个班级在各分数段的人数多少。

密度分布：

• 适合比较不同数据范围或不同样本量的分布形状（不受区间宽度和样本量影响）。
• 例如：比较满分 100 分的考试和满分 150 分的考试的分数分布形状，或样本量差异极大的两组数据的分布差异。
• 是核密度曲线（KDE）的基础，常用于概率统计分析（如正态分布、t 分布等）。

2. 散点图添加抖动

散点图给 x 、y 轴数据添加轻微随机抖动，防止数据点完全重叠（比如多个样本在同一坐标时，抖动后能看清数量）

参考资料

[1] [美]克林顿 W. 布朗利 (Clinton W. Brownley). Python数据分析基础[M]. 陈光欣，译. 北京：人民邮电出版社，2017:192-208.