基础字符串总结
讨厌字符串...
关于字符串的一些定义:
- \(|s|\) 表示字符串 \(s\) 的长度。
- \(s_{l,r}\) 表示字符串 \(s\) 位置 \(l \sim r\) 上的字符所连接成的子串。
- \(\mathrm{lcp(s,t)}\) 表示字符串 \(s\) 与 \(t\) 的最长公共前缀,\(\mathrm{lcs(s,t)}\) 则表示为最长公共后缀。
1. 哈希(Hash)
没什么可说的,将字符串表示为 \(p\) 进制数,模数为 ^#%@&$。
可能有哈希冲突,通常可用双哈希(不过我懒)。
一些题也可以用哈希冲过去,是一个不错的工具。
2. kmp算法
3. 后缀数组(SA)
一个稍难但极好用的算法。
3.1 定义
- 设 \(su_i\) 表示字符串 \(s\) 中以 \(s_i\) 开头的后缀。
- \(rk_i\) 表示 \(su_i\) 在所有后缀中的字典序排名。
- \(sa_i\) 表示 \(s\) 所有后缀中排名为 \(i\) 的后缀的开始位置,其与 \(rk\) 互逆,即 \(sa_{rk_i} = rk_{sa_i} = i\)。
- \(ht_i\) 表示 \(su_{sa_{i-1}}\) 与 \(su_{sa_i}\) 的最长公共前缀,即 \(|lcp(su_{sa{i-1}},su_{sa_i})|\),且 \(ht_1 = 0\)。
3.2 后缀排序
后缀排序算法可以求出后缀数组,用的是倍增法。
假设我们已经求出来所有 \(2^w\) 级的子串,即所有 \(s_{i,i+2^w-1}\) 的排名 \(rk_i\),则我们可以通过拼接 \(rk_i\) 与 \(rk_{i+2^w}\) 来求出 \(2 ^{w+1}\) 级的子串,所以我们可以通过构造 \((rk_i,rk_{i+2^w})\) 的二元组,经过排序得到所有 \(2^{w+1}\) 级子串的排名,直接快排是 \(O(n\log^2{n})\) 的,观察到排名的值域非常小,可以通过基数排序来优化到 \(O(n\log{n})\),不过这样常数还是极大。
考虑一种优化,我们发现对于二元组的第二维,如果 \(i + 2^w > n\) 则我们可以直接排到最前面,然后我们把剩下的按照 \(sa_i\) 的顺序依次填入 \(sa_i - 2^w\) 即可,这样我们就可以用桶排序直接排第一维,常数较小。
(还有 DC3 \(O(n)\) 算法,不过不想学 : ( )
int n,m,p;
char c[N];
int sa[N],rk[N],ork[N<<1],id[N],cnt[N];
bool cmp(int a,int b,int w){return ork[a] == ork[b] && ork[a + w] == ork[b + w];}
//若与相等的不加,否则加
int main(){
scanf("%s",c+1);
n = strlen(c+1),m = 128;
for(int i = 1;i <= n;i++)cnt[rk[i] = c[i]]++;
for(int i = 1;i <= m;i++)cnt[i] += cnt[i-1];
for(int i = n;i >= 1;i--)sa[cnt[rk[i]]--] = i;
for(int w = 1;;w <<= 1,m = p,p = 0){
for(int i = n - w + 1;i <= n;i++)id[++p] = i;
for(int i = 1;i <= n;i++)
if(sa[i] > w)id[++p] = sa[i] - w;
memset(cnt,0,sizeof cnt);
for(int i = 1;i <= n;i++)cnt[rk[i]]++;
for(int i = 1;i <= m;i++)cnt[i] += cnt[i-1];
for(int i = n;i >= 1;i--)sa[cnt[rk[id[i]]]--] = id[i];
p = 0;
memcpy(ork,rk,sizeof rk);
for(int i = 1;i <= n;i++)rk[sa[i]] = cmp(sa[i-1],sa[i],w) ? p : ++p;
if(p == n)break;
}
for(int i = 1;i <= n;i++)printf("%d ",sa[i]);
printf("\n");
return 0;
}
3.3 height 数组
求 \(ht\) 主要依据的是一个性质:\(ht_{rk_i} \geq ht_{ri_{i-1}} - 1\)。
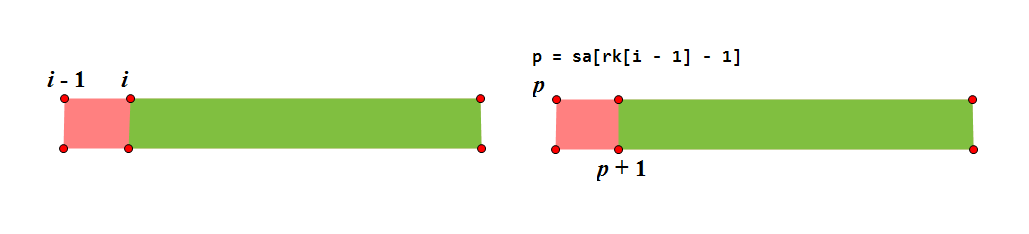
(图源为 Alex_wei)
- 证明,首先我们设 \(p\) 为 \(sa_{rk_{i-1} - 1}\),即 \(i-1\) 后缀的前一名,则若 \(ht_{rk_{i-1}} > 1\),则必然有 \(s_{i} = s_{p+1}\),又因为 \(p\) 的排名小于 \(i-1\),则 \(p+1\) 的排名一定小于 \(i\),而排名在 \(p+1\) 与 \(i\) 之间的 LCP 长度一定不小于 \(ht_{rk_{i-1}} - 1\) (因为字典序是递增的),即得 \(ht_{rk_{i}} \geq ht_{rk{i-1}} - 1\),得证。
所以我们可以 \(O(n)\) 求出 \(ht\) 数组。
for(int i = 1;i <= n;i++){
if(p)p--;
while(c[i + p] == c[sa[rk[i] - 1] + p])p++;
ht[rk[i]] = p;
}
3.4 应用
3.4.1 求两个后缀的 LCP
设 \(\mathrm{lcp(i,j)} = \mathrm{lcp(su_i,su_j)}\),若 \(i \not = j\) 则有:
即 \(i\) 与 \(j\) 的后缀最大公共前缀是在两排名之间 \(ht\) 数组最小值,可以 ST 表维护。
3.4.2 本质不同子串个数
首先总数有 \(\dbinom {n+1} 2\)。
我们考虑重复子串,对于从 \(i\) 开始的子串,重复的子串个数即最长公共前缀长度,即 \(ht_{rk_i}\)。
得到本质不同子串个数为:\(\dbinom {n+1} 2 - \sum\limits_{i = 2}^n ht_i\)。
3.4.3 结合单调栈
我们观察 \(ht\) 数组,可以把其看作 \(n\) 个矩形的并,而知周所众单调栈可以解决类似问题,如我们要求 \(\sum\limits_{1\leq i < j \leq n} \mathrm{lcp(su_i,su_j)}\),我们考虑依据排名依次加入,则可以看作加入一个宽为 \(1\) 高为 \(ht_i\) 的矩形,而我们求得答案即矩形面积和,即可单调栈维护,复杂度 \(O(n)\)。
3.5 例题
复制一遍拼下,然后就是板子。
首先我们把 \(S_0\) 串与 \(S\) 拼接起来(常用技巧),中间补个分割符 #,跑个后缀数组。
然后我们考虑每个 \(i\) 与 \(S\) 匹配,我们假设当前已经匹配长度为 \(p-1\) 的串了,则我们可以找出 \(|lcp(i+p-1,|S_0|+p+1)|\),ST 表维护即可,我们循环三次,若匹配长度超过 \(|S|\) 则答案加 \(1\)。
复杂度 \(O(n\log{n})\)。
III P3181 [HAOI2016] 找相同字符
答案就是一些 \(\mathrm{lcp(i,j)}\) 的和。
我们首先拼接一下,然后我们考虑后缀的贡献,只需要跑三遍 SA + 单调栈 即可(即 总的贡献 - 两字符串自己对自己的贡献)。
首先可以想到本质不同子串,但本题会加字符,如果我们加在字符串尾部的话,整个字符串的后缀都会改变,这是不好的,所以我们考虑反转倒序加入,这样字符串仅仅只是多了一个后缀,其他后缀都不变,考虑如何求不同子串,即求,当前后缀与所有后缀的最长前缀,我们只需维护一个 \(set\),考虑当前排名前后的 \(\mathrm{lcp}\) 即可。
复杂度 \(O(n\log{n})\)。
V P5341 [TJOI2019] 甲苯先生和大中锋的字符串
题目即求字符串中出现次数 恰好 为 \(k\) 的子串中,长度出现次数最多的长度是多少。
我们考虑如何找恰好出现 \(k\) 次的子串,在每个后缀字符串中,我们发现出现 \(k\) 次,即在 \(ht\) 数组里有长度为 \(k\) 的连续排列(因为排序后相同的前缀一定在一个连续的区间),则可以枚举排名,假设当前为 \(i\),则我们只需要找到 \(i \sim i+k-1\) 的最长前缀即可,ST 表即可,而又因为恰好,这说明不能有长度小于等于 \(\mathrm{lcp(i-1,i)}\) 与 \(\mathrm{lcp(i+k-1,i+k)}\) 的子串(因为超过 \(k\) 次了),这样我们差分一下,找个最大值即可。
复杂度 \(O(n\log{n})\),注意多组数据,\(i+k\) 可能会越位,注意清空。
首先有差分,然后转化为求 \(n\) 个串的最长公共子串。
然后拼接到一起,考虑在 \(n\) 个串中选出 \(n\) 个起点,则答案即为 \(n\) 个起点最小与最大 \(rk\) 之间 \(ht\) 最小值,即 \(\max\limits_{1\leq l < r\leq n}\min\limits_{k=l+1}^{r}ht_k\),条件就是 \([l,r]\) 的排名区间内必须包含 \(n\) 个子串的至少一个点,可以用桶简单处理,外层可以双指针处理,内层可以 ST 表 也可以 单调队列。
复杂度 \(O(n\log{n})\),若 DC3 + 单调队列 则为 \(O(n)\)。
VII P4094 [HEOI2016/TJOI2016] 字符串
首先我们知道,一个后缀 \(i\) 与一些后缀的 \(\mathrm{lcp}\) 是与 \(rk_i\) 最近的后缀的 \(rk\) 值的 \(\mathrm{lcp}\),根据 应用I 易证,所以我们只需要找到区间 \(a \sim b\) 中 \(rk_c\) 的 前后继,可用 可持久化线段树 解决,当然也可以用可持久化平衡树。
但是这是错的,原因是因为有右界,导致我们需要对每个答案取 \(min\),导致 \(rk_c\) 的 前后继 不一定最大(可能被取 \(min\) 了),我们需要二分 \(mid\),单调性是显然的,则我们只需要找区间 \([a,b-mid+1]\) 中的结果即可,码量稍大(约 4K)。
: )
最后别忘记与 \(d-c+1\) 取 \(min\),复杂度 \(O(n\log^2{n})\)。
为啥暴力 SA 跑的比正解快 几十倍?
VIII P2178 [NOI2015] 品酒大会
好题,首先我们考虑 r 相似 的性质,可以发现 r 相似,即在 \(ht\) 数组中一段连续区间 \([l,r]\) 使得任意 \(i \in [l,r]\) 都有 \(ht_i \geq k\),则该排名区间任意两个后缀都有 r 相似,这样的操作可以用并查集维护 \(ht\) 数组中大于等于 \(k\) 的区间,我们只需要从大到小枚举 \(k\),合并即可。
然后考虑算答案,第一问是好求的,在并查集合并时加上 \(size_x \times size_y\) 即可,第二问有乘积,负负得正,我们需要维护并查集内 最大值,次大值,最小值,次小值,则答案即为 \(max(mx1 \times mx2,mi1\times mi2)\)。
复杂度 \(\mathcal{O}(n\log{n})\),若 SA 用 DC3 则复杂度为 \(\mathcal{O}(n\alpha(n))\)。
这个 \(\mathcal{O}\) 好好看 : )
IX CF822E Liar
好题,先拼接,题目中有一句话是 "按照原顺序合并",这启发我们可以枚举每个 \(i\),贪心找 \(\mathrm{lcp}\),复杂度是 \(\mathcal{O}(n^2)\) 的。
观察数据范围看到 \(x\) 较小,可以考虑 DP,设 \(f_{i,j}\) 表示在前 \(i-1\) 个字符组成的字符串中,选最多 \(j\) 个不相交的子串所构成字符串与 \(T\) 串前缀的最长匹配长度。
对于每一个 \(f_{i,j}\),令 \(k = \mathrm{lcp(i,l1 + 2 + f_{i,j})}\),则若不匹配 \(i\),则 \(f_{i+1,j}\gets\max(f_{i+1,j},f_{i,j})\);若匹配 \(i\),则 \(f_{i+k,j+1}\gets\max(f_{i+k,j+1},f_{i,j} + k)\)。
复杂度 \(\mathcal{O}(n\log{n} + nx)\)。
神仙题,不过 \(\mathcal{O}(n^2)\) 95pts 谁写正解啊!,首先 \(AABB\) 可拆分,设 \(f_i/g_i\) 表示以 \(i\) 结尾/开头的 \(AA\) 造型方案数,则答案即为 \(\sum\limits_{i=1}^{n-1}f_i \times g_{i+1}\)。
然后就牛了,我们钦定一个 \(len\),我们每隔 \(len\) 标记一个点,则 \(AA\) 需要恰好经过两个点,我们假设 \(i,j \ (i + len = j)\),我们令 \(l = \mathrm{lcs(i,j)}\),\(r = \mathrm{lcp(i+1,j+1)}\),则若 \(l + r \geq len\),则该区间存在 \(AA\),考虑 \(f\),可知结尾点可以是 \([j+max(0,len-l),j+min(len-1,r)]\) 区间内的点,差分即可,\(g\) 同理。
不懂的可以画图,下图绿色部分即可用起点区间,棕色部分即可以结尾区间。
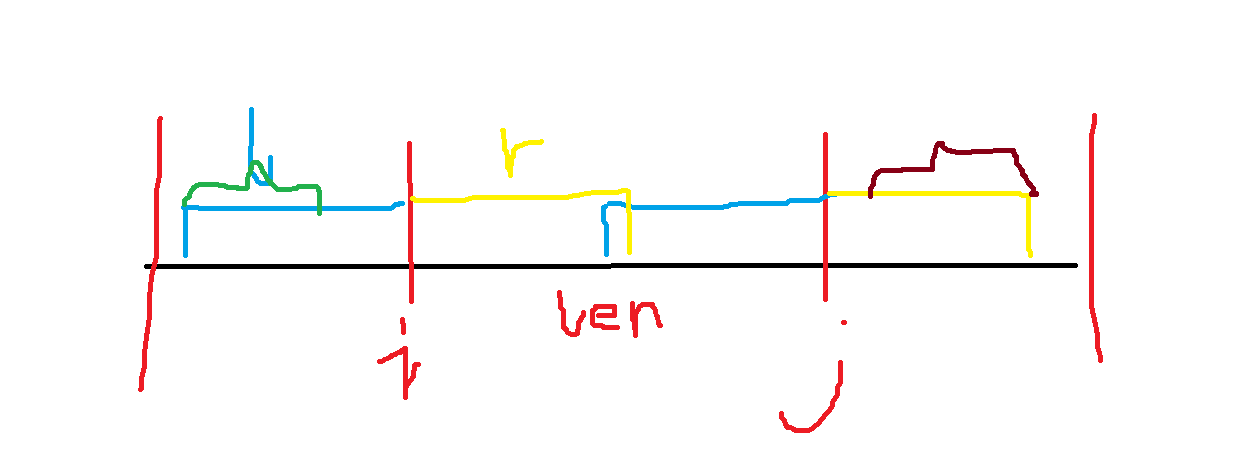
枚举 \(len\) 的复杂度是调和级数的,总复杂度 \(\mathcal{O}(Tn(\log{n} + \ln{n}))\)。
XI P4081 [USACO17DEC] Standing Out from the Herd P
神秘题。
首先拼接,注意这样多个串拼接要用 不同拼接符号,所有字串总答案即 \(\dbinom {n+1} 2\)。
然后我们按排名枚举,对于每个 \(i\),我们需要知道前面所有后缀的 \(\mathrm{lcp}\),即 \(ht_i\),而且要知道后面 不是当前字符串 的 \(\mathrm{lcp}\),所以我们可以找到每一段 在同一字符串 中的区间 \([l,r]\),倒序依次减去 \(\max(ht_i,\min\limits_{k=i+1}^{r+1}ht_k)\) 的贡献,复杂度是 \(\mathcal{O}(n)\) 的。
复杂度 \(\mathcal{O}(n\log{n})\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号