前 k 小问题期末考

这里的前 \(k\) 小是指 \(k\le 2\times 10^5\) 的问题，并且要完全求出第 \(1\sim k\) 小的值。并且大概率不具有可二分性。

入门篇

P2048 超级钢琴，P5283 异或粽子，CF280D

这个三个题说明了：这类题目可以用堆维护当前状态集合 \(S\)，初始 \(S\) 加入第一小状态。

每次取出 \(S\) 中最小的状态，并且把 \(S\) 的若干后继状态加入堆。

• 后继状态可以理解为在 \(S\) 中扩展一步得到的状态，此时需要保证加入完前 \(k\) 小的后继状态时，第 \(k+1\) 小一定在堆中。

此时维护得好大概率可以做到 \(\mathcal{O}((n+k)\log n)\)。

拓展篇

树

给定一棵 \(n\) 个点的树，每个点有一个点权 \(a_i\)。求其点权和第 \(k\) 小的连通块的点权和。

\(1\le n,k\le 2\times 10^5,1\le a_i\le 10^9\)

推荐题解

P6646

有 \(N\) 个商品，每个商品有个种类 \(a_i\)，有个价格 \(c_i\)。

对于第 \(j\) 个种类，必须购买个数位于 \([x_j,y_j]\) 的商品，即最少购买 \(x_j\) 个，最多购买 \(y_j\) 个该种类的商品。

您需要求出前 \(K\) 种便宜的方案所需的价钱，如果没有这样的方案，请输出 \(-1\)。

• 特别的，如果有相同钱数，但是具体方案不相同的，算作两种方案。

\(1\le N,M,K\le 2\times 10^5,1\le a_i\le M,1\le c_i\le 10^9,0\le x_j\le y_j\le N\)

推荐题解

---

在认真 阅读/编写 这两题题解后，容易总结出共性：

有可能 \(S\) 的后继状态很多，每次直接暴力拓展可能会退化到 \(\mathcal{O}(nk\log n)\)。就坠机了。

我们考虑如下转化，\(A,B,C,D\) 是 \(S\) 的后继状态，\(a,b,c,d\) 是增加的代价：

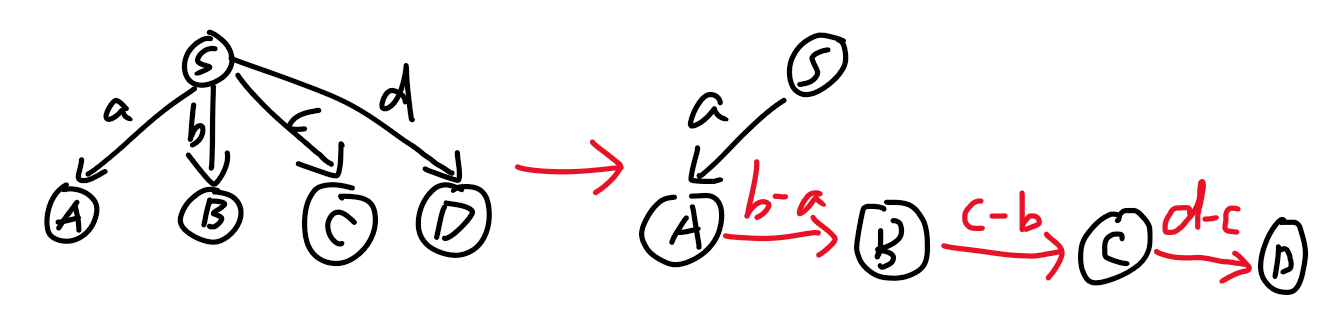
我们做个类似差分的东西，就能使得每个状态的后继状态唯一！注意这里必须限制 \(a\le b\le c\le d\)。

实际过程大概形如：\(S\to S+\{x\},S\to S-\{y\}+\{z\},\cdots\)。

• \(x\) 是 \(S\) 可扩展的最小状态

• \(y\) 是 \(S\) 最后被加入的位置，\(z\) 大概是 \(y\) 的后继

大部分这类题都可以通过这样把后继状态变成 \(\mathcal{O}(1)\) 个，可能需要多维护几个量就是了。