蓝桥三十一天刷题（python组）||灵能传输蓝桥oj196

题目描述

求解

求解本题有两个关键。

第一个是，从题给

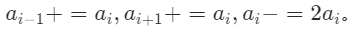
中，要联想到前缀和的变化：

s'i-1=si，s'i=si-1，s'i+1=s+1

其中s'是变化后的前缀和，s是原数组a的前缀和。

可以发现，对于s'中，没有出现新的值。所以问题转化为对s'排序，并找到最小的两元素之差（的绝对值，下省略）。

第二个是，

在前缀和中，sn和s0的位置不能发生变化，只能一个在最后面，一个在最前面。s0不变因为a1的计算依赖于它；sn不变是因为an的计算依赖于它。所以我们对s排序完之后，要建立一个新数组存尽量满足两项之差最小的前缀和。

下图来自：

灵能传输(前缀和 + 贪心)_Panse·的博客-CSDN博客

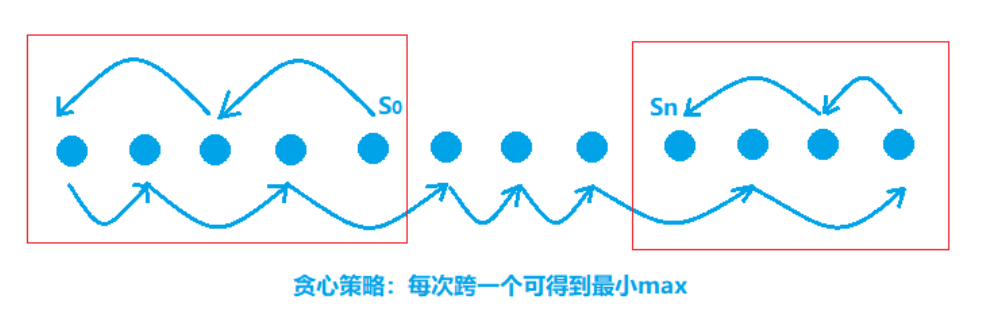
为什么需要隔一个元素取呢？可以用反证法想，如果不隔元素，最左边的元素到下一个元素值的差就很大了；如果隔两个元素或者更多，差也是比隔一个元素要大。所以使用隔一个元素的策略最优。

python代码如下：

T=int(input())
for _ in range(T):
    n=int(input())
    a=list(map(int,input().split()))
    s=[0]+a
    for i in range(1,n+1):
        s[i]+=s[i-1]
        
    s0,sn=0,s[n]
    if s0>sn:
        s0,sn=sn,s0

    s.sort()
    for i in range(n+1):
        if s[i]==s0:
            ind_s0=i
            break
    for i in range(n,-1,-1):
        if s[i]==sn:
            ind_sn=i
            break

    maxa=0
    L,R=0,n
    vis=[False]*(n+1)
    new_s=[0]*(n+1)
    
    for i in range(ind_s0,-1,-2):
        vis[i]=True
        new_s[L]=s[i]
        L+=1
    for i in range(ind_sn,n+1,2):
        vis[i]=True
        new_s[R]=s[i]
        R-=1
    for i in range(n+1):
        if vis[i]==False:
            new_s[L]=s[i]
            L+=1
    

    for i in range(1,n+1):
        maxa=max(abs(new_s[i]-new_s[i-1]),maxa)

    print(maxa)