蓝桥三十一天刷题（python组）||二分法总结

从区间值的类型来分，二分法可分为整数二分和实数二分。顾名思义，整数二分的区间值都是整型类型，实数二分的区间值是浮点型。本文先进行整数二分模板的讲解，而后解析两道相关例题；然后展示实数二分模板，并通过一道例题明确其用法。

整数二分

模板公式

def check():
    #具体的check函数
    pass

def bin_search(a,n,x):
    l,r=-1,n+1
    while l+1!=r:
        mid=(l+r)//2
        if check():
            l=mid
        else:
            r=mid
        return (l or r) #选取需要的部分进行返回

本模板的初始l、r值取数组边界外的值，规定当l+1==r时跳出循环。可以看出，在二分结束时，满足check（）的条件的都是l左边的值，不满足的都是右边的值。下图给出当数组有3个元素的示意图。

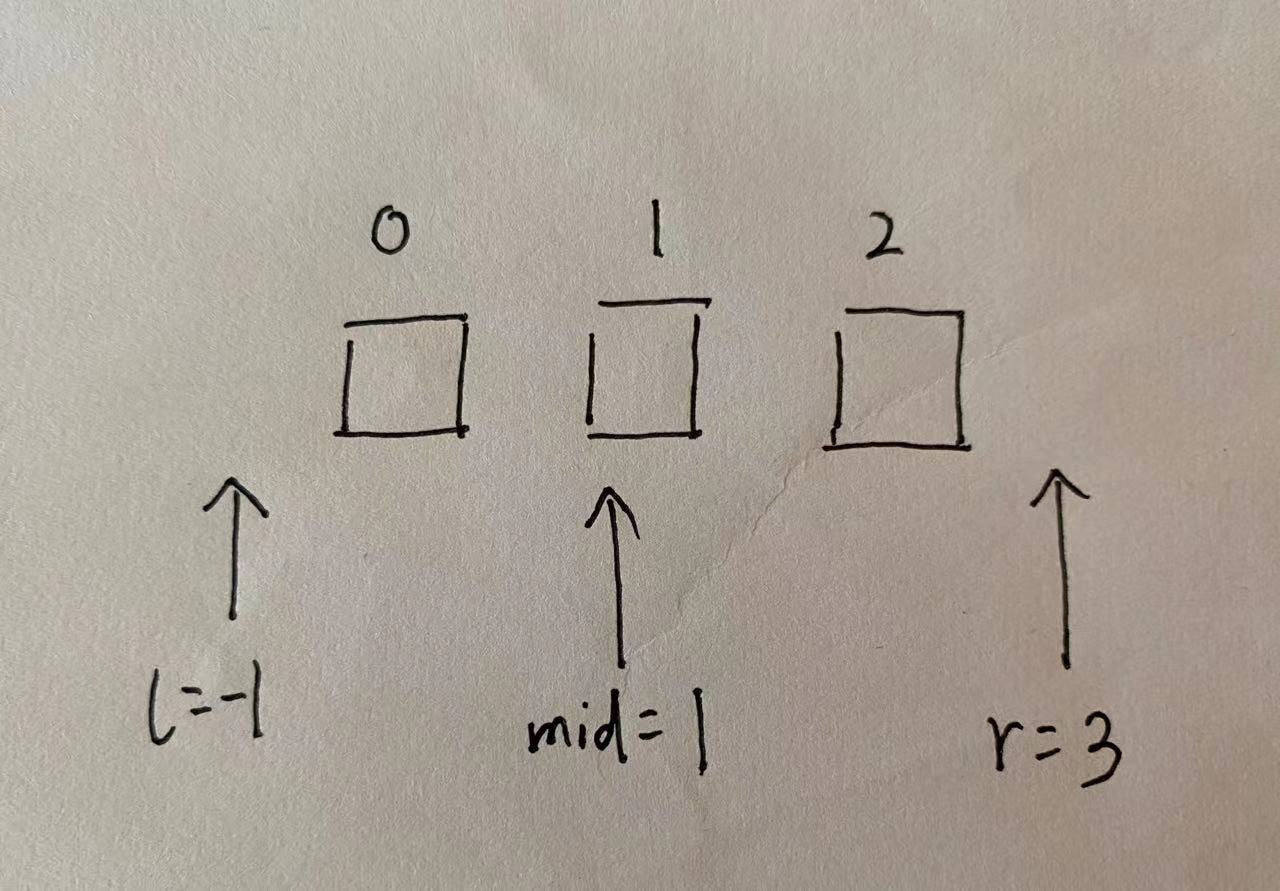
我们可通过修改l和r来满足题目条件。

比如给定一个数组x=[1,2,3,3,4,5,5,6]：

情况一：找比5小的最小数。

check函数可写成：

def check(mid):
    if mid<5:
        return True
    return False

主函数 return l。

情况二：找等于5的最小数。

check函数和情况一一样，主函数return r。

情况三：找等于5的最大数。

check函数可写成：

def check(mid):
    if mid<=5:
        return True
    return False

主函数return l。

情况四：找大于5的最小数。

check函数和情况三一样，主函数return r。

题解

蓝桥oj2145 求阶乘

求解

k=int(input())

def cal_zero(N):
    cnt=0
    while N!=0:
        N=N//5
        cnt+=N
    return cnt

l,r=-1,int(1e19)
while l+1!=r:
    mid=(l+r)//2
    if cal_zero(mid)<k:
        l=mid
    else:
        r=mid

if(cal_zero(r)==k):
    print(r)
else:
    print(-1)
    

可以发现，随着k的增大，N的阶乘也是单调不减的，因此可以用二分法。

用二分法需要一个判断条件。如果想要数字末尾有0，那它一定有因子2和5。对于阶乘而言，因子2的个数比因子5要多得多，可直接考虑因子5的个数。可通过循环累除后求和的方式得到因子5的个数。

蓝桥oj2143 最少刷题数

求解

（1）模拟法（通过率40%）

见下文。

蓝桥三十一天刷题（python组）||第四天_树欲静而风不止慢一点吧的博客-CSDN博客

（2）n次二分法（通过率70%）

这篇文章解释了bisect库中bisect_left()和bisect_right()的用法。

Python3二分查找库函数bisect(), bisect_left()和bisect_right()介绍_YMWM_的博客-CSDN博客

题目可以转化为，求一个数在有序数列中的映射，以求比它小的和大的分别有多少个数。建立sa作有序数组，通过二分确定映射位置。

from bisect import *
n=int(input())
a=list(map(int,input().split()))
sa=sorted(a)
max_a=sa[-1]
res=[0]*(n)

def check(cur,old):
    fewer=bisect_left(sa,cur)
    if cur!=old:fewer-=1
    more=n-bisect_right(sa,cur)
    if more>fewer: return True
    return False
    
for i in range(n):
    l,r=a[i]-1,max_a
    while l+1!=r:
        mid=(l+r)//2
        if check(mid,a[i]):
            l=mid
        else:
            r=mid
    res[i]=r-a[i]

print(*res)

（3）一次二分法（通过率100%）

我们发现需要多刷题的人，最后刷到的题数都是一样的。因此我们只需要找到最少刷题数，用一次二分找最后需要刷到的题数，再对所有人的刷题数进行check()就好了。

from bisect import *
n=int(input())
a=list(map(int,input().split()))
sa=sorted(a)
max_a=sa[-1]
min_a=sa[0]
min_i=a.index(min_a)
res=[0]*(n)

def check(cur,old):
    fewer=bisect_left(sa,cur)
    if cur!=old:fewer-=1
    more=n-bisect_right(sa,cur)
    if more>fewer: return True
    return False


l,r=a[min_i]-1,max_a
while l+1!=r:
    mid=(l+r)//2
    if check(mid,a[min_i]):
        l=mid
    else:
        r=mid

goal=r

for i in range(n):
    if check(a[i],a[i]):
        res[i]=goal-a[i]
    else:
        res[i]=0

print(*res)

实数二分

模板公式

while写法

eps=1e-6 #精度
while r-l>eps:
    mid=l+r>>1
    if check(mid):    r=mid
    else:        l=mid

for写法

for i in range(100):
    mid=(l+r)/2
    if check(mid):    r=mid
    else:    l=mid

推荐用while写法，题目一般会给精度要求，循环次数也没for多。

题解

蓝桥oj764 一元三次方程求解

求解

n=input().split()
a,b,c,d=eval(n[0]),eval(n[1]),eval(n[2]),eval(n[3])

def y(x):
    return a*x**3+b*x**2+c*x+d

esp=0.001
for i in range(-100,100):
    L,R=i,i+1
    y1,y2=y(L),y(R)
    if y1==0:
        print("{:.2f}".format(L),end=" ")
    if y1*y2<0:
        while(R-L)>=0.001:
            mid=(L+R)/2
            if y(mid)*y(R)<=0: L=mid
            else: R=mid
        print("{:.2f}".format(L),end=" ")

根据题给条件“根与根之差的绝对值 ≥1”，可知在(-100,100)内任意长度为1的区间内，只存在小于等于1个的根。因此，可把(-100,100)200等分，对每一小区间采用二分法，判断条件为mid和R的函数值是否异号或有一个为0。