第十四届蓝桥杯三月真题刷题训练——第 27 天 （牛客网）

储物点的距离

求解

前缀和处理ai（通过率30%）

n,m=map(int,input().split())
a=[0]+list(map(int,input().split()))
sa=[0]*(n)
for i in range(1,n):
    sa[i]=sa[i-1]+a[i]
b=[0]+list(map(int,input().split()))
for i in range(m):
    x,l,r=map(int,input().split())
    cost=0
    for j in range(l,r+1):
        cost+=b[j]*abs(sa[j-1]-sa[x-1])
    print(cost%1000000007)

优化1

把绝对值拆开分类讨论，只需维护两个前缀和数组，可以把每次查询的时间复杂度降为O（1）。具体实现如下：

让sa下标从i=2开始，表示第i-1到第i个储物点的距离，i=2时就是第1个储物点到第2个储物点的距离。那么对于[L,R]区间内的每个j，有cost=b[j]*abs(sa[j]-sa[x])。

可发现当j>=x时，cost=b[j]*(sa[j]-sa[x])

当j<x时，cost=b[j]*（-(sa[j]-sa[x])

那么当所有的j都>=x，即r<=x时，

记c=a.*b，sc为c的前缀和。记sb为b的前缀和，则有

cost=sc[r]-s[l-1]-sa[x]*(sb[r]-sb[l-1])

当x<=l时，则有

cost=-（sc[r]-s[l-1]-sa[x]*(sb[r]-sb[l-1]))，即是x>=r的表达式取相反数

当x在l和r之间时，

对于[l,x-1]和[x,r]有

cost1=sc[x-1]-s[l-1]-sa[x]*(sb[x-1]-sb[l-1])

cost2=-（sc[r]-s[x-1]-sa[x]*(sb[r]-sb[x-1]))

cost=cost1+cost2

n,m=map(int,input().split())
a=[0,0]+list(map(int,input().split()))
sa=[0]*(n+1)
for i in range(2,n+1):
    sa[i]=sa[i-1]+a[i]

b=[0]+list(map(int,input().split()))
sb=[0]*(n+1)
for i in range(1,n+1):
    sb[i]=sb[i-1]+b[i]

c=[0]+[sa[i]*b[i] for i in range(1,n+1)]
sc=[0]*(n+1)
for i in range(1,n+1):
    sc[i]=c[i]+sc[i-1]

for i in range(m):
    x,l,r=map(int,input().split())
    cost=0
    if x>=r:
        cost=sa[x]*(sb[r]-sb[l-1])-(sc[r]-sc[l-1])
    elif x<=l:
        cost=-sa[x]*(sb[r]-sb[l-1])+(sc[r]-sc[l-1])
    else:
        cost=-sa[x]*(sb[r]-sb[x-1])+(sc[r]-sc[x-1])
        cost+=sa[x]*(sb[x-1]-sb[l-1])-(sc[x-1]-sc[l-1])
    print(cost%1000000007)

卡在了十连重测。。

优化2

在计算时对取余操作进行优化，规则见文章：

取余运算规则_取余运算规律_zhenggy_的博客-CSDN博客

本题我们要算(a*b+c)%mod，可使用(a+b)%mod和(a*b)%mod的规则倒推回去。

于是(a*b+c)%mod=((a%mod*b%mod)%mod+c%mod)%mod。

不过还有个问题，可能有种情况是，原先a*b-c大于0，而(a%mod*b%mod）-(c%mod)小于0，这怎么办？

先不要管python怎么负数取余，先想想怎么让(a%mod*b%mod）-(c%mod)变成正数并%mod出现正确的结果。只需加上mod就可以了。可以这么理解：把(a%mod*b%mod）相当于d%mod，d向前减去n个mod，(c%mod)则相当于c向前减去m个mod，这两个结果数值上都没有mod大。只要加一个mod给d，那么新的d减去c必然为正数。

而python的负数取余，就可以帮你免去这一步+mod，非常方便。

然而，通过率还是30%。。。要不就是30%，要不就是十连重测。。。

mod=1000000007

n,m=map(int,input().split())
a=[0,0]+list(map(int,input().split()))
sa=[0]*(n+1)
for i in range(2,n+1):
    sa[i]=sa[i-1]+a[i]
 
b=[0]+list(map(int,input().split()))
sb=[0]*(n+1)
for i in range(1,n+1):
    sb[i]=sb[i-1]+b[i]
 
c=[0]+[sa[i]*b[i] for i in range(1,n+1)]
sc=[0]*(n+1)
for i in range(1,n+1):
    sc[i]=c[i]+sc[i-1]
 
for i in range(m):
    x,l,r=map(int,input().split())
    cost=0
    if x>=r:
        cost=(sa[x]*(sb[r]-sb[l-1])%mod-(sc[r]-sc[l-1])%mod)%mod
    elif x<=l:
        cost=(-sa[x]*(sb[r]-sb[l-1])%mod+(sc[r]-sc[l-1])%mod)%mod
    else:
        cost=(-sa[x]*(sb[r]-sb[x-1])%mod+(sc[r]-sc[x-1])%mod)%mod
        cost+=(sa[x]*(sb[x-1]-sb[l-1])%mod-(sc[x-1]-sc[l-1])%mod)%mod
        cost+=mod
    print(cost%mod)

如果把+mod都写了，就会稳定出现通过率30%，不会出现十连重测。。。代码如下

优化3

mod=1000000007

n,m=map(int,input().split())
a=[0,0]+list(map(int,input().split()))
sa=[0]*(n+1)
for i in range(2,n+1):
    sa[i]=sa[i-1]+a[i]
 
b=[0]+list(map(int,input().split()))
sb=[0]*(n+1)
for i in range(1,n+1):
    sb[i]=sb[i-1]+b[i]
 
c=[0]+[sa[i]*b[i] for i in range(1,n+1)]
sc=[0]*(n+1)
for i in range(1,n+1):
    sc[i]=c[i]+sc[i-1]
 
for i in range(m):
    x,l,r=map(int,input().split())
    cost=0
    if x>=r:
        cost=(sa[x]*(sb[r]-sb[l-1]+mod)%mod-(sc[r]-sc[l-1]+mod)%mod+mod)%mod+mod
    elif x<=l:
        cost=(-sa[x]*(sb[r]-sb[l-1]+mod)%mod+(sc[r]-sc[l-1]+mod)%mod+mod)%mod+mod
    else:
        cost=((-sa[x]*(sb[r]-sb[x-1]+mod)%mod+(sc[r]-sc[x-1]+mod)%mod+mod)%mod+mod)%mod
        cost+=((sa[x]*(sb[x-1]-sb[l-1]+mod)%mod-(sc[x-1]-sc[l-1]+mod)%mod+mod)%mod+mod)%mod
        cost=(cost+mod)
    print(cost%mod)

数学考试

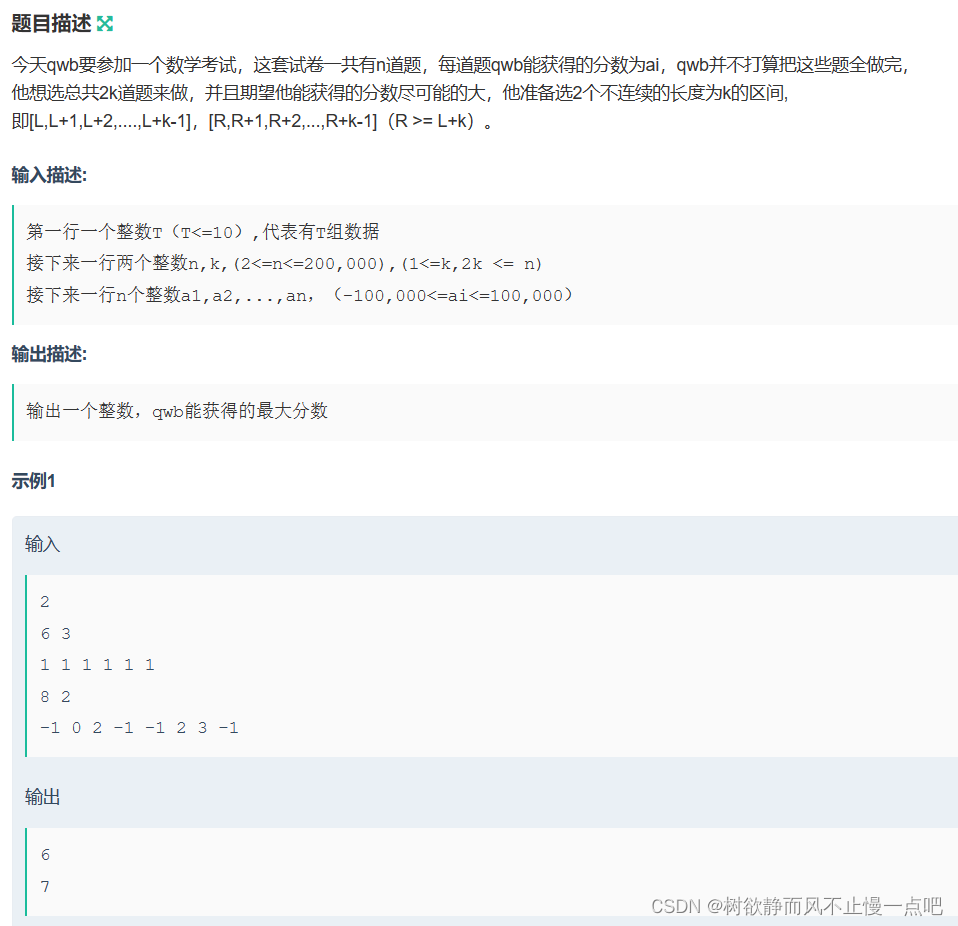
求解

通过率50%。使用s存取分数前缀和，搞两个指针分别对应两个区间头，遍历第一个指针的同时让第二个指针运动。

T=int(input())
for _ in range(T):
    n,k=map(int,input().split())
    a=[0]+list(map(int,input().split()))
    s=[0]*(n+1)
    for i in range(1,n+1):
        s[i]=a[i]+s[i-1]
    
    p1=1
    p2=k+1
    s1=s[k]-s[0]
    s2=s[2*k]-s[k]
    ms=s1+s2
    while p1+2*k-1<=n:
        s1=s[p1+k-1]-s[p1-1]
        p1+=1
        p2=p1+k
        while p2+k-1<=n:
            s2=s[p2+k-1]-s[p2-1]
            p2+=1
            s12=s1+s2
            if s12>ms:
                ms=s12
    print(ms)

优化

其实有O（n）的解法，毕竟有了前缀和，求区间和时间复杂度都是O（1），那直接开一个循环，找最大值和它后面的极大值，且它们两个没有重叠部分就好了。然而通过率33.3%。。。其他超时。max函数很慢吗？还是1e5太大？

T=int(input())
for _ in range(T):
    n,k=map(int,input().split())
    a=[0]+list(map(int,input().split()))
    s=[0]*(n+1)
    for i in range(1,n+1):
        s[i]=a[i]+s[i-1]
    
    p=k
    max1=-1e5
    max2=-1e5
    while p+k<=n:
        max1=max(max1,s[p]-s[p-k])
        max2=max(max2,max1+s[p+k]-s[p])
        p+=1
    print(max2)

优化2

不用max，用if。通过率依旧是33.3%。用time模块测输入样例，发现运行时间差不多。费解。

T=int(input())
for _ in range(T):
    n,k=map(int,input().split())
    a=[0]+list(map(int,input().split()))
    s=[0]*(n+1)
    for i in range(1,n+1):
        s[i]=a[i]+s[i-1]
    
    p=k
    max1=-1e5
    max2=-1e5
    while p+k<=n:
        if max1<(s[p]-s[p-k]):
            max1=(s[p]-s[p-k])
        if max2<max1+s[p+k]-s[p]:
            max2=max1+s[p+k]-s[p]
        p+=1
    print(max2)