基础操作

张量 tensor

• 创建行向量： x = torch.arange(12)

• 改变张量形状： x.reshape(3, 4)

  • 如果知晓目标维长度，剩余维长度可用-1代替，而不必手动计算，如 x.reshape(-1, 4) 或 x.reshape(3, -1)

• 访问张量各轴长度： x.shape

• 访问张量元素总数： x.numel()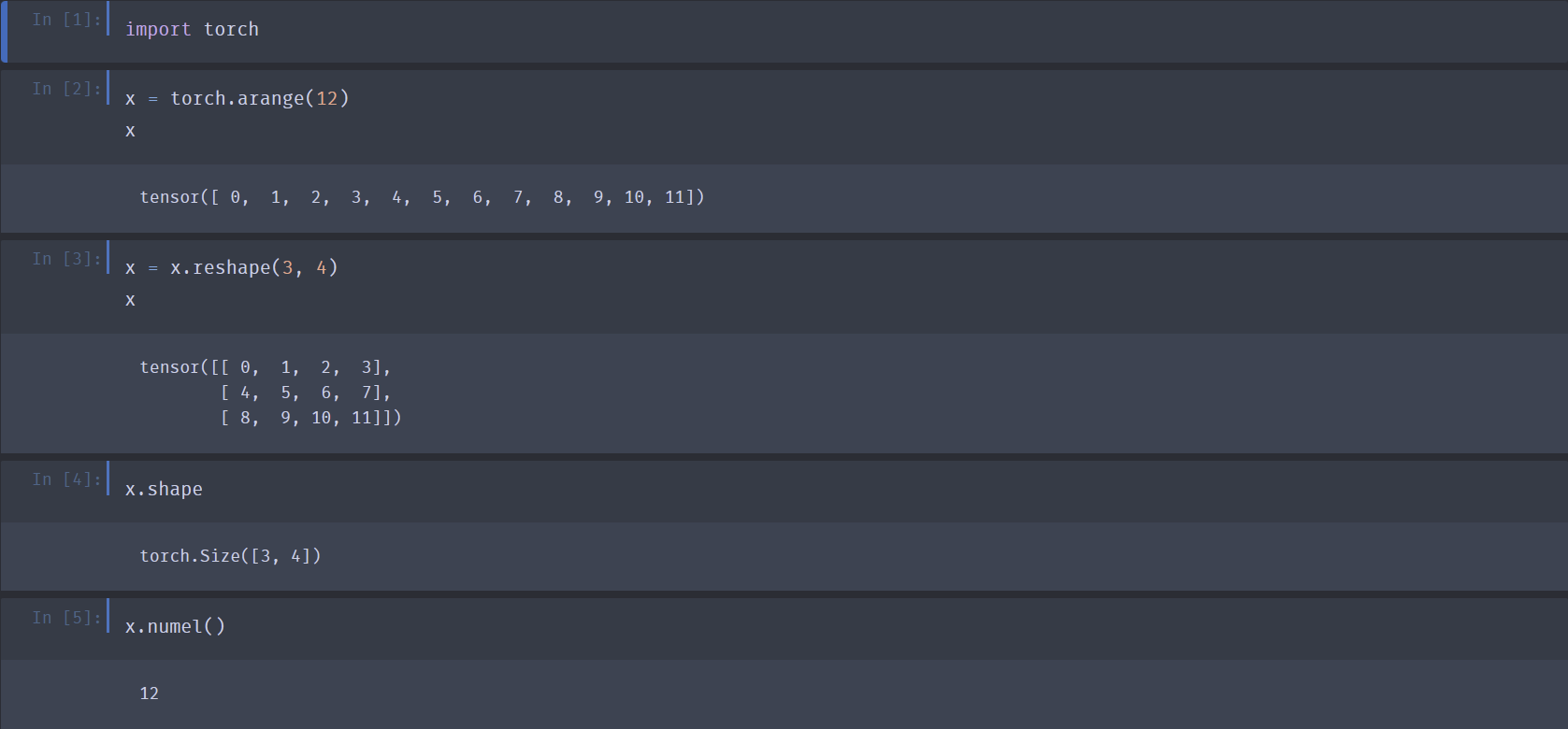

  

• 生成元素均为 0 的张量： x = torch.zeros(3, 4). 注：python默认用浮点型（float32），如果想要指定形式可以利用dtype： x = torch.zeros(3, 4, dtype=torch.int32)

• 生成元素均为 1 的张量： x = torch.ones(3, 4). 注：python默认用浮点型（float32），如果想要指定形式可以利用dtype： x = torch.ones(3, 4, dtype=torch.int32)

• 生成元素从 \(\mu = 0, \delta = 1\) 正态分布随机采样的张量： x = torch.randn(3, 4)

• 张量赋值： x = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

• 改变张量中某一个元素的值： x[0, 1] = 1 。 注意：直接 x[0, 1] 的返回结果是一个二维各轴长均为1的张量，提取元素时应带上 .item() ！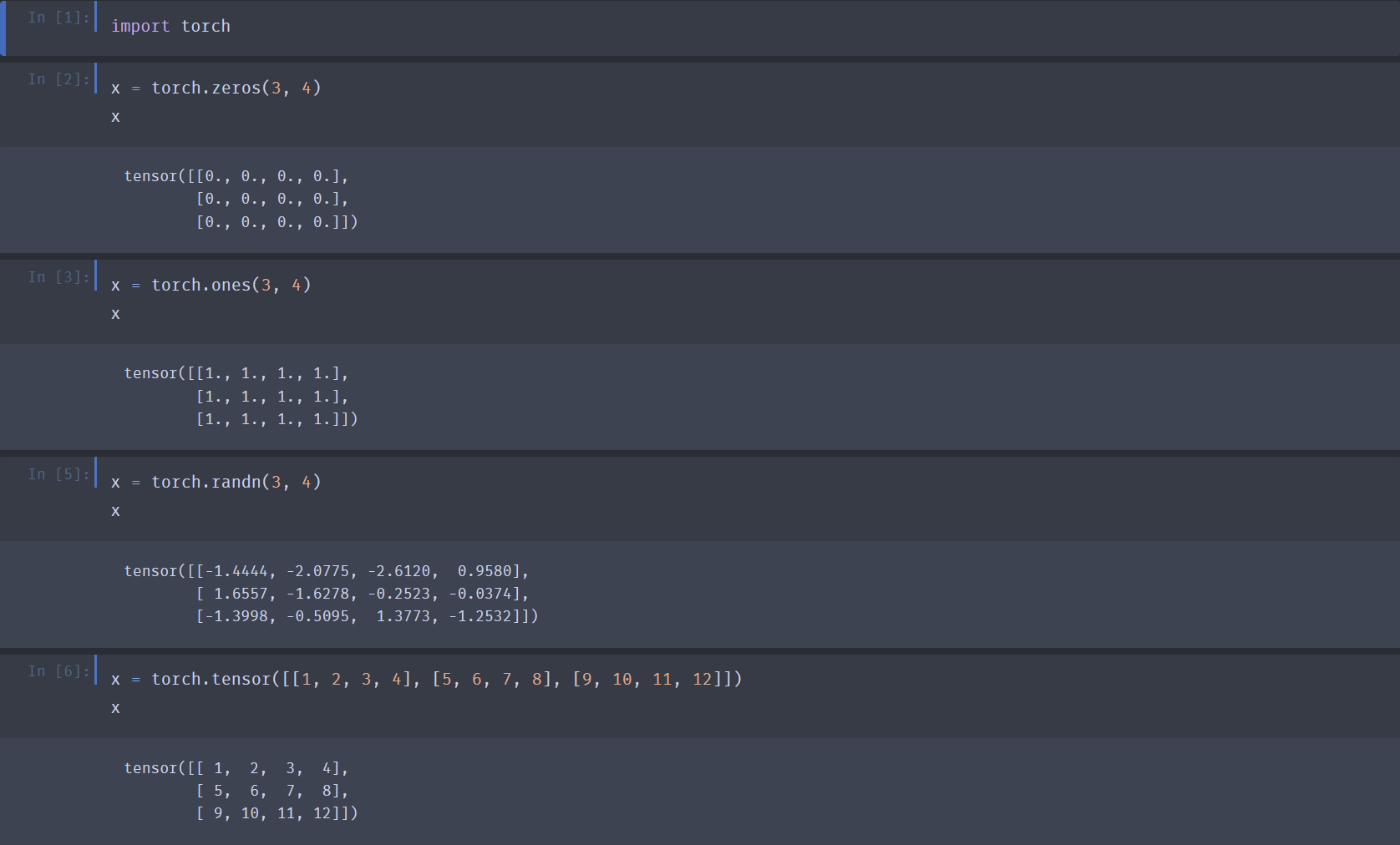

  

• 相同形状张量按元素加、减、乘、除、乘方：x + y, x - y, x * y, x / y, x ** y

  

• 判断两个相同形状张量每个位置上对应元素相同、不同： x == y, x != y

  • 注意返回值是一个True/False张量。

  

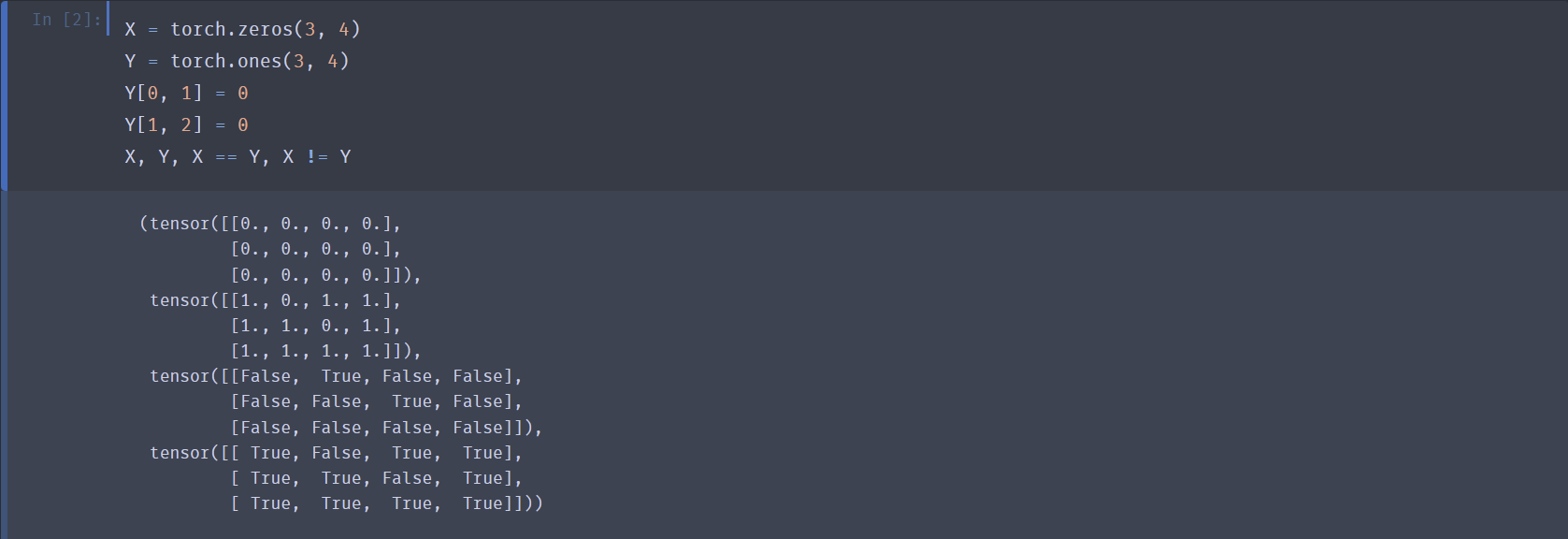
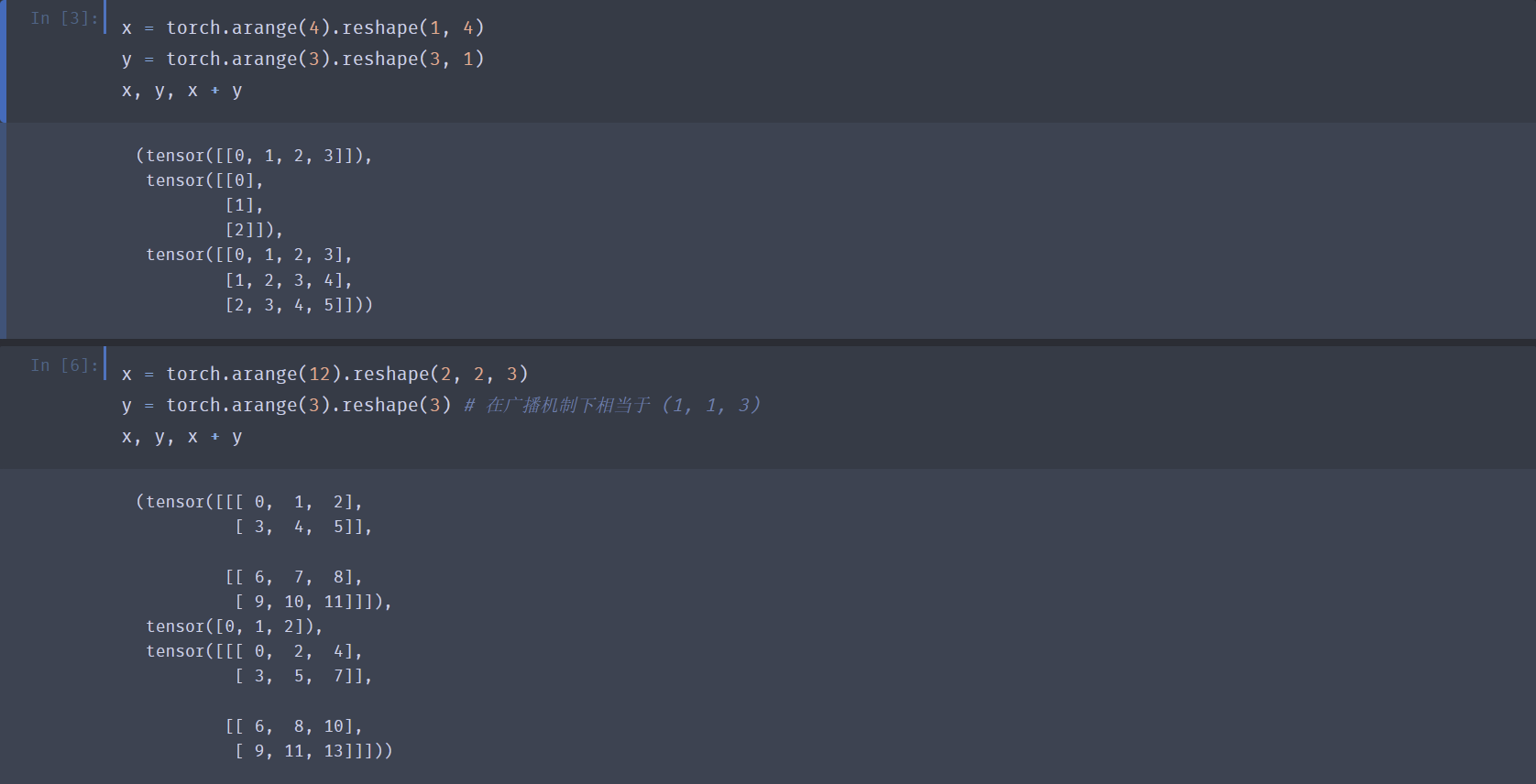
• 广播机制：不同形状张量进行逐元素运算（+, -, *, /, **, ==, != etc.）时，会执行广播机制，通过沿长度为 \(1\) 的轴复制元素，使两个张量形状变得相同，再执行一般的逐元素运算。具体的：

  1. 若两张量维数不同，则会在维数更小的张量左侧补“1”.
  2. 之后逐维比较：
     1. 若该维两张量长度相同 => 无需广播
     2. 若某一张量该维长度为 \(1\) => 将该张量沿此轴广播
     3. 否则，两张量无法进行逐元素运算，报错
  3. 广播后的两张量形状一致，按一般的逐元素运算法则进行计算。

  

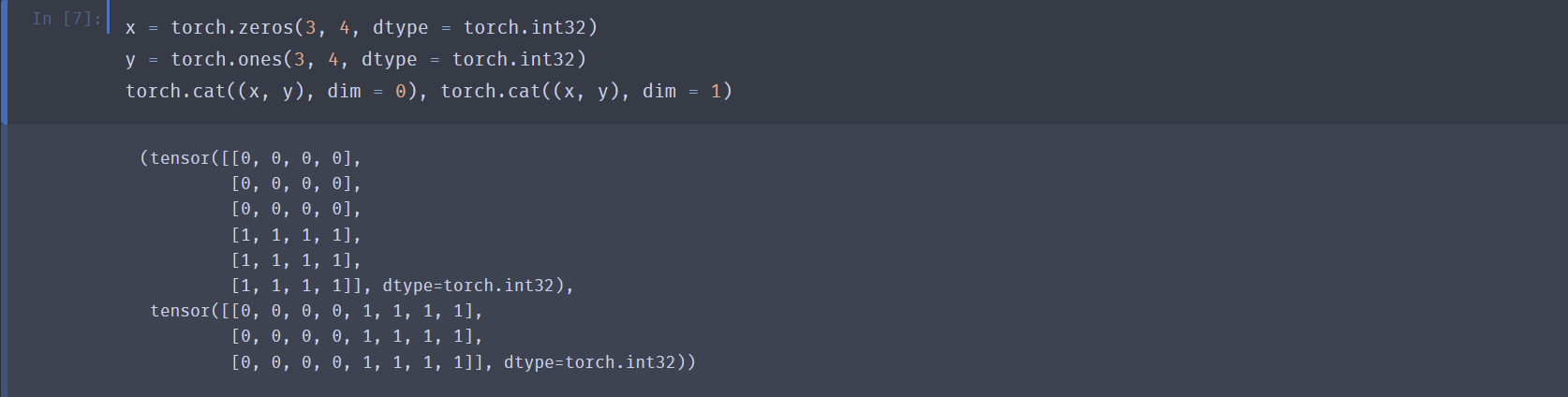
• 张量连接： torch.cat((x, y), dim = 0)

  • 维数（dim）从 0 计起，和 reshape 的顺序是相同的。从中括号嵌套的角度讲，最外层中括号是第 \(0\) 维，向内一层是第 \(1\) 维，以此类推，而包裹用逗号分隔的连续数字的那一维就是第 \(n-1\) 维。
  • 按某一维连接时，该维大小可以不同，但剩余维的大小必须相同。
  • 连接不改变张量的维数。

  

• 标量、向量、矩阵分别可以用0维、1维、2维张量表示。

  • 在 Pytorch 中，向量并没有“列”与“行”的概念。
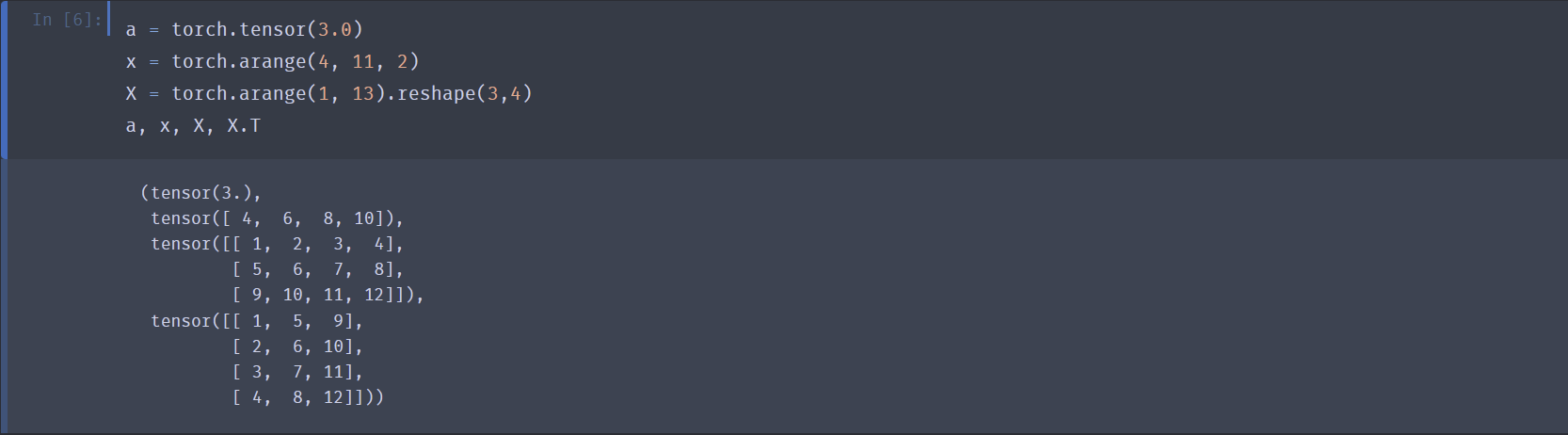
  • 矩阵的转置： X.T （注意：仅可对二维张量使用该操作，对于其它维张量使用该操作是非法的，但是仅有Warning而没有Error）.

  

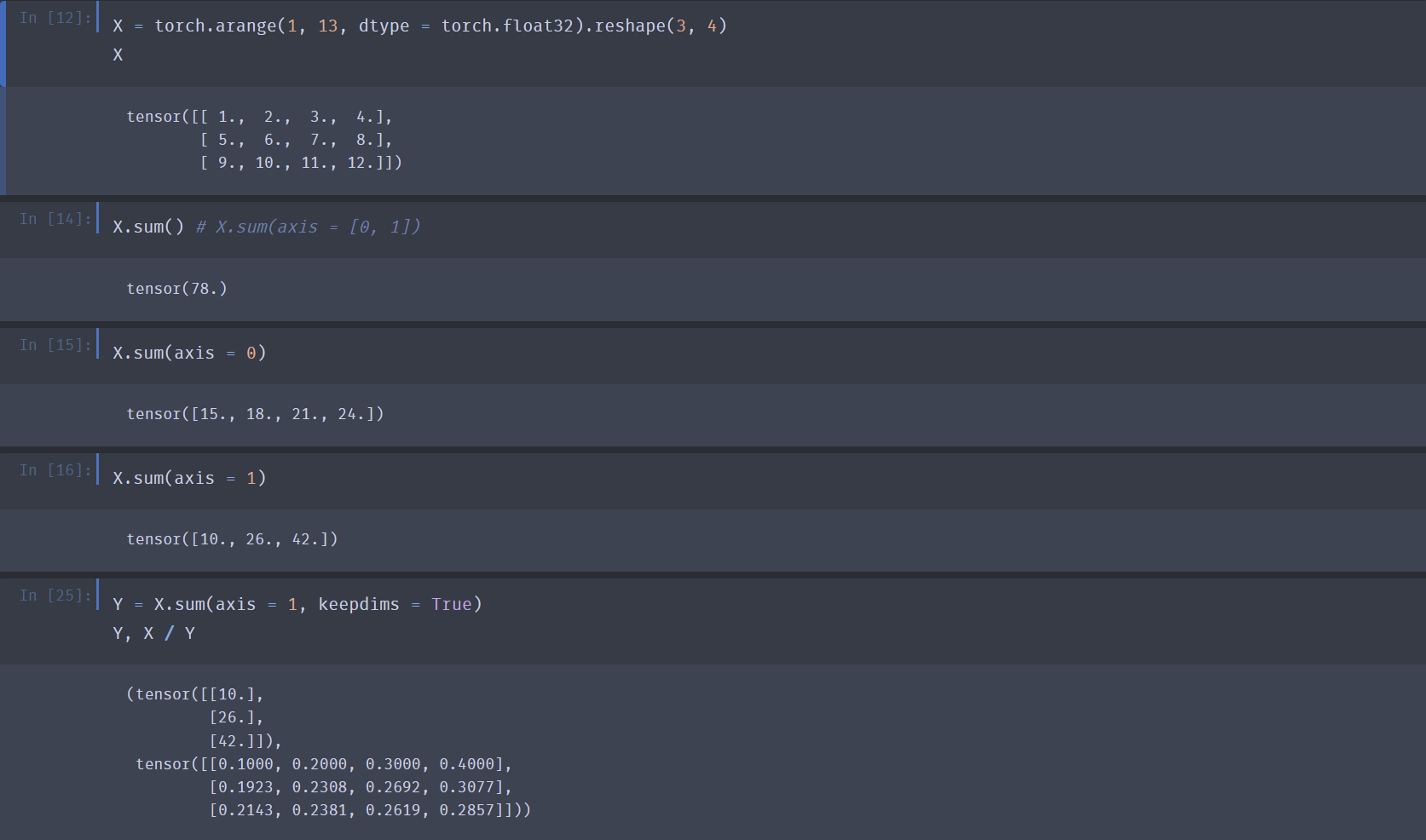
• 求和： X.sum()

  • 求和是一种常见的降维操作。
  • 默认情况下，求和会沿所有轴降维，即计算张量所有元素的和，使其变为一个标量。
  • 可以通过 axis 指定沿哪个/些轴降维求和。
  • 可以通过设置 keepdims 的值实现非降维求和，之后可以利用广播机制得到与原张量相同形状的张量。

• 求平均值： X.mean()

  • 求平均值是一种常见的降维操作。
  • 默认情况下，求平均值会沿所有轴降维。
  • 可以通过 axis 指定沿哪个/些轴降维求平均值。
  • 求均值操作只可以作用于浮点型或复数型的数据，整型不可以。

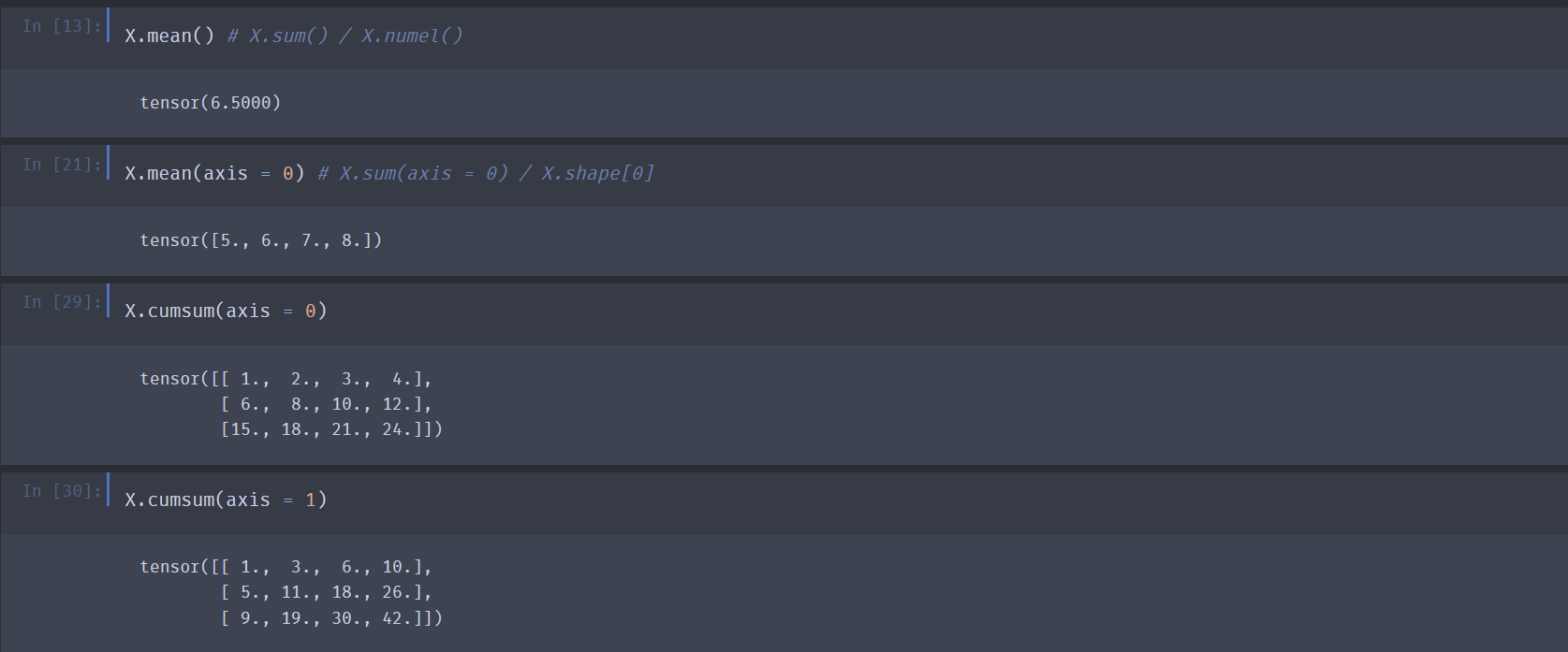
• 求沿某一方向前缀累加和： X.cumsum(axis = 0)

  • cumsum 是一种不降维操作。

  
  

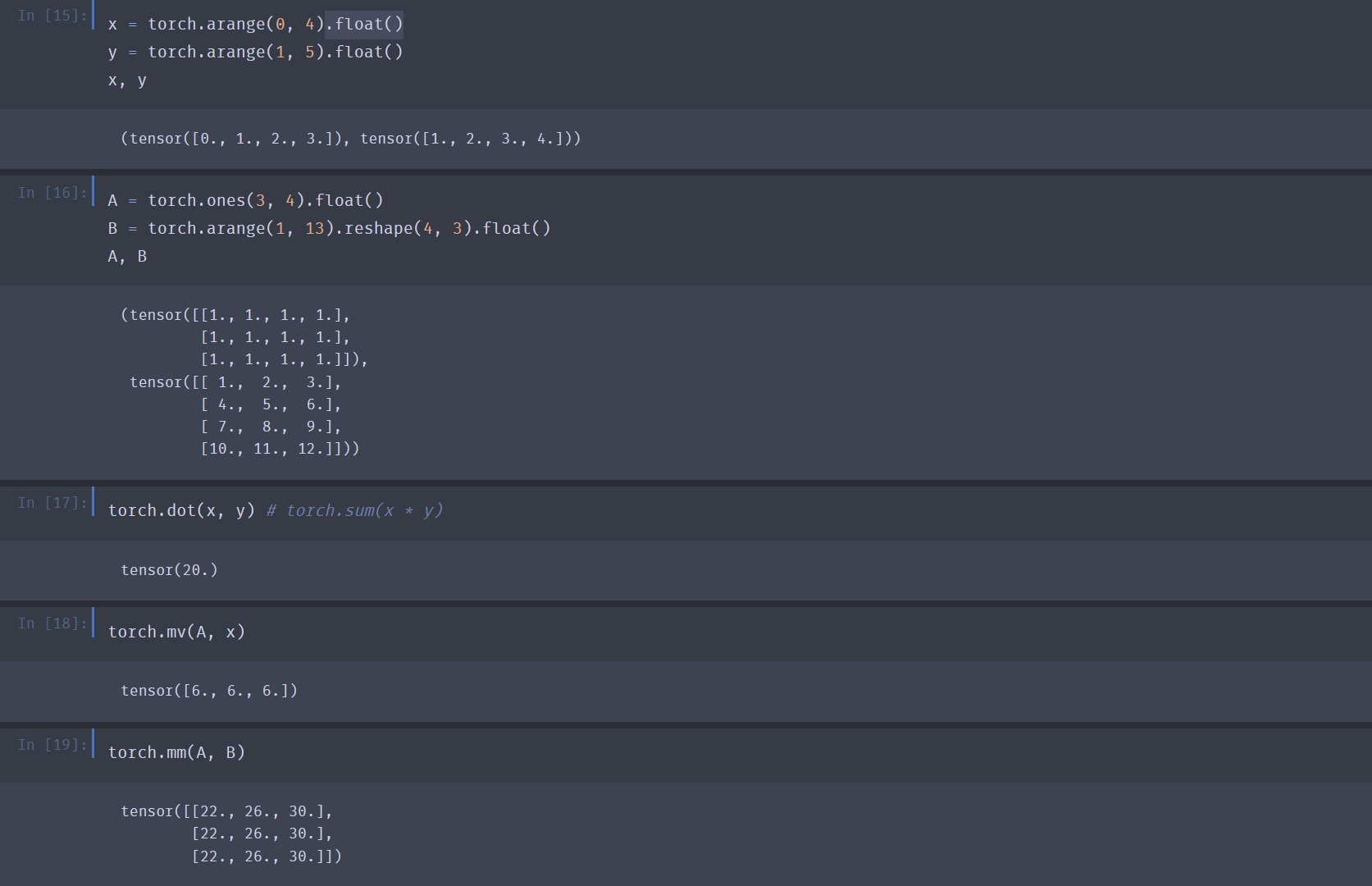
• 向量点乘： torch.dot(x, y)

• 矩阵向量乘： torch.mv(A, x)

• 矩阵矩阵乘： torch.mm(A, B)

  • mv()和mm()均要求参与运算的张量的元素类型为浮点型，整型不可以。

  

• 范数

  \(L_p\) 范数的定义为: \(\lVert x \rVert_{p} = (\sum\limits_{i=1}^{n} |x_i|^p )^{\frac{1}{p}}\).

  常用范数分别是 \(L_1\)范数 \(\lVert x \rVert_{1} = \sum\limits_{i=1}^{n} |x_i|\) ，和 \(L_2\)范数 \(\lVert x \rVert_{2} = \sqrt{\sum\limits_{i=1}^{n} {x_i}^2 }\) ：

  • \(L_1\) 范数： torch.abs(x).sum()
  • \(L_2\) 范数： torch.norm(x)

  

绘图 matplotlib

例：绘制函数在某一点处切线 d2l ver, simp ver

%matplotlib inline    # 让 matplotlib 绘出的图直接嵌在 jpt notebook 的输出单元格中，而非独立窗口。
from matplotlib_inline import backend_inline  # backend_inline 模块提供对当前所用绘图后端（这里是与 Jupyter 集成的 inline 后端）的细粒度控制。
from mxnet import np, npx  # 从 MXNet 深度学习框架里导入 np：MXNet 的 NumPy 兼容张量接口；npx：MXNet 的扩展算子接口。
from d2l import mxnet as d2l  # 导入《动手学深度学习》提供的 MXNet 版工具包 d2l。

npx.set_np()  # 激活 MXNet 的 NumPy 兼容模式。只有调用这句后，mxnet.numpy 中的算子才能像原生 NumPy 那样自动执行延迟计算与自动微分。

def f(x):
    return 3 * x ** 2 - 4 * x 

def numerical_lim(f, x, h):  # 传入函数 f、点 x、步长 h，返回该点的近似导数值。
    return (f(x + h) - f(x)) / h

def use_svg_display():  #@save
    backend_inline.set_matplotlib_formats('svg')  # 强制 inline 后端以 SVG 矢量格式 输出图形。矢量图在放大时不会失真，适合教材 / 论文场景。

def set_figsize(figsize=(3.5, 2.5)):  #@save
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize  # 设置默认画布尺寸（宽 3.5 英寸、高 2.5 英寸），并且先调用 use_svg_display 保证 SVG 输出。

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    # 对给定 Axes 对象一次性完成坐标轴常用设置：
    axes.set_xlabel(xlabel)  # xlabel / ylabel：坐标轴标题
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)  # xscale / yscale：坐标刻度类型（线性/对数）
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)  # xlim / ylim：坐标范围
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)  # legend：图例
    axes.grid()  # grid：打开网格线
    
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    # plot 是封装的绘制函数
    # 若只给 X（或 Y 是一维），自动把它当成 Y，内部补空 X。
	# 支持多条曲线（X、Y 为列表），每条曲线自动循环使用 fmts 中的格式字符串。
	# 自动调用前面定义的 set_figsize、set_axes，简化调用者代码。
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
    
x = np.arange(0, 3, 0.1)  # 在 [0,3) 区间以 0.1 为步长生成一维张量，供给后续作图和计算。
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])  #  调用上面封装的 plot 函数：
# x 作为横坐标；两条纵坐标曲线：f(x) = 3x²−4x 本身 和 直线 2x−3（切线)；x 轴标签 'x'，y 轴标签 'f(x)'，图例区分两条线；添加图例：两条曲线分别对应的文字。

自动微分 automatic differentiation

数学定义：(以下 \(\mathbf{x}\) 和 \(\mathbf{y}\) 均为列向量)

• 标量对标量的微分：\(\dfrac{\partial y}{\partial x}\)
• 标量对向量的微分：\(\dfrac{\partial y}{\partial \mathbf{x}} = \begin{bmatrix} \dfrac{\partial y}{\partial x_1}, \dfrac{\partial y}{\partial x_2}, \cdots , \dfrac{\partial y}{\partial x_n} \end{bmatrix}\)
• 向量对标量的微分：\(\dfrac{\partial \mathbf{y}}{\partial x} = \begin{bmatrix} \dfrac{\partial y_1}{\partial x} \\\ \dfrac{\partial y_2}{\partial x} \\\ \cdots \\\ \dfrac{\partial y_m}{\partial x} \end{bmatrix}\)
• 向量对向量的微分：\(\dfrac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix} \dfrac{\partial y_1}{\partial \mathbf{x}} \\\ \dfrac{\partial y_2}{\partial \mathbf{x}} \\\ \cdots \\\ \dfrac{\partial y_m}{\partial \mathbf{x}} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial y_1}{\partial x_1}, \dfrac{\partial y_1}{\partial x_2}, \cdots , \dfrac{\partial y_1}{\partial x_n} \\\ \dfrac{\partial y_2}{\partial x_1}, \dfrac{\partial y_2}{\partial x_2}, \cdots , \dfrac{\partial y_2}{\partial x_n} \\\ \vdots \\\ \dfrac{\partial y_m}{\partial x_1}, \dfrac{\partial y_m}{\partial x_2}, \cdots , \dfrac{\partial y_m}{\partial x_n} \end{bmatrix}\)

链式法则： \(\dfrac{\partial y}{\partial x} = \dfrac{\partial y}{\partial u_n} \dfrac{\partial u_n}{\partial u_{n-1}} \cdots \dfrac{\partial u_2}{\partial u_1} \dfrac{\partial u_1}{\partial x}\)

• 正向累积： \(\dfrac{\partial y}{\partial x} = \dfrac{\partial y}{\partial u_n} ( \dfrac{\partial u_n}{\partial u_{n-1}} ( \cdots (\dfrac{\partial u_2}{\partial u_1} \dfrac{\partial u_1}{\partial x}) ) )\)
• 反向传播 (backpropagation)： \(\dfrac{\partial y}{\partial x} = ( ( ( \dfrac{\partial y}{\partial u_n} \dfrac{\partial u_n}{\partial u_{n-1}} ) \cdots ) \dfrac{\partial u_2}{\partial u_1} )\dfrac{\partial u_1}{\partial x}\)

操作：

• 设定张量记录计算图开关： x.requires_grad_(True)

  • Pytorch 会对 requires_grad == True 的张量自动隐式构建计算图。每执行一步张量操作，立即把对应节点插进计算图。给中间结果挂上 grad_fn=<...>，记下反向传播时要用到的“倒带函数”。当最后调用反向传播函数时，再沿着这张隐式建好的图反向走一遍，算出所有叶子张量的梯度。

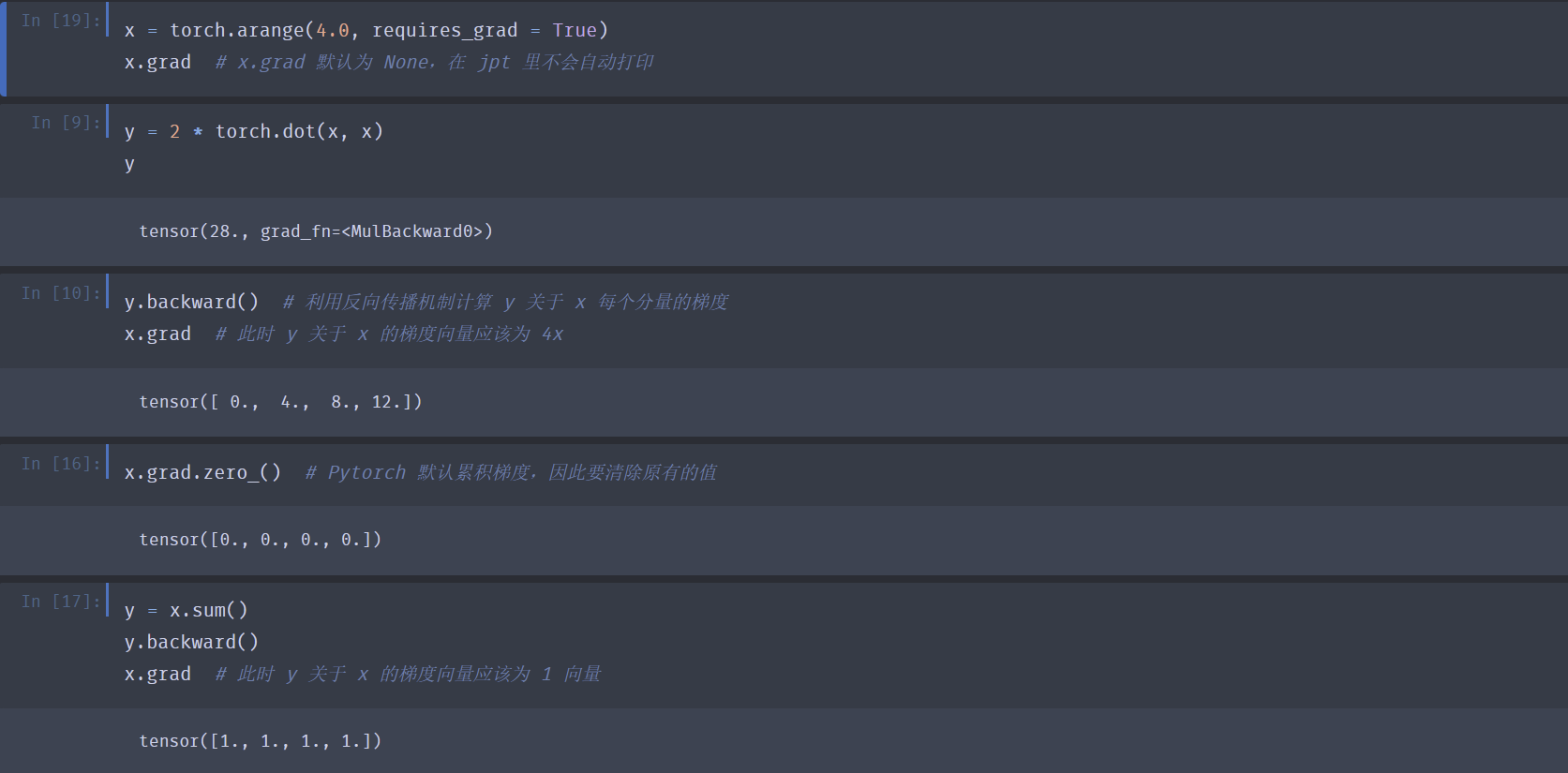
• 张量的梯度： x.grad

  • 默认是 None.
  • 叶子节点的梯度默认会累积，因此如果计算不同函数对同一向量的梯度的时候要记得清零。
  • 中间节点默认不会存梯度，调用中间节点的 grad 的结果一般是 None。如果想要保留可以调用 u.retain_grad() .

• 将张量的梯度清零： x.grad.zero_()

  • 清零操作不可对 None 执行。

  

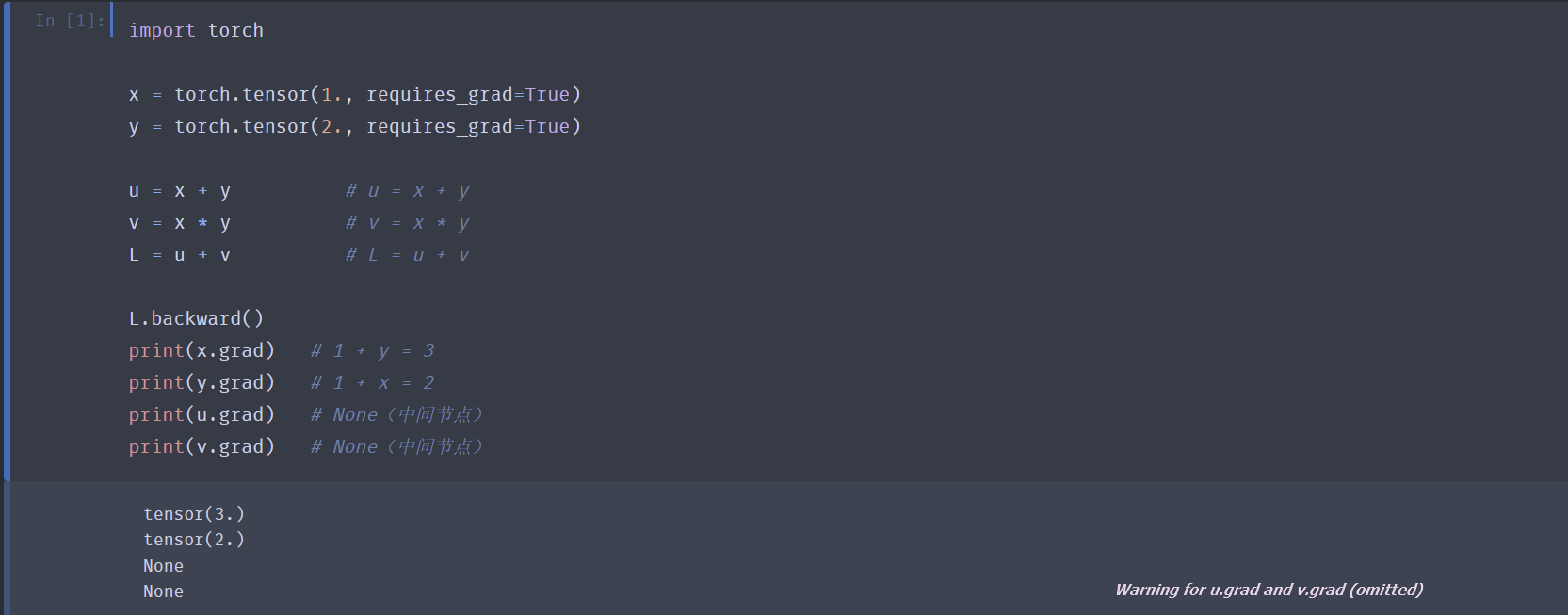
• 反向传播计算梯度： L.backward()

  • PyTorch 在调用 L.backward() 时，会沿着所有从 L 能够逆向到达、且 requires_grad=True 的叶子张量的路径同时传播梯度；每一条可行路径都会根据链式法则把局部梯度乘进去，最后在叶子节点处把来自不同路径的贡献求和。
  • 例如对于计算图 ：

    x ---> u --> L
      \ /     /
      / \    /
    y ---> v 
    

    1. 计算图中的节点情况
       叶子：x、y（用户显式创建，is_leaf=True）
       中间：u、v（由运算产生，is_leaf=False）
       输出：L（标量）
    2. 前向时 PyTorch 做了什么
       每做一次运算就生成一个 grad_fn=<OpBackward> 对象，并把它挂到结果上；
       这些 grad_fn 组成了一个有向无环图（DAG）。
       因此 L 的 grad_fn 指向 u 和 v，u、v 的 grad_fn 又指向 x 和 y。形成如下结构：

       L.grad_fn
        ├── u.grad_fn  ──► x.grad_fn 
        │                └─ y.grad_fn 
        └── v.grad_fn  ──► x.grad_fn 
                          └─ y.grad_fn 
       

    3. 反向传播的历程
       步骤 1：把 L 的梯度初始化为 1（因为是标量）。
       步骤 2：从 L 开始反向拓扑遍历整张图：
       先走到 u 和 v，分别用 MulBackward0、AddBackward0 之类的函数算出 ∂L/∂u、∂L/∂v
       再沿着 u、v 各自的父边继续走到 x、y：
       对 x：存在两条路径
       L→u→x 贡献 (∂L/∂u)(∂u/∂x)
       L→v→x 贡献 (∂L/∂v)(∂v/∂x)
       PyTorch 把它们相加后写进 x.grad
       对 y：同理，把 L→u→y 与 L→v→y 两条路径的和写进 y.grad
    4. 谁最终有 .grad？
       叶子节点 + requires_grad=True：x、y 会收到梯度
       中间节点：u、v 的 grad_fn 只是用来计算局部梯度，本身不会保留 .grad

  

分离计算：希望某些计算移动到计算图之外（在计算梯度的时候视作常数），可以调用拆卸函数来获得副本 tem = y.detach()

• 注意区分几种常见的赋值操作：

线性神经网络

线性回归 linear regression

线性模型

对于一个样本，线性模型的表示式为

其中 \(\hat{y}\) 为预测结果（\({y}\) 为真实结果），\(w_i\) 为权重，\(x_i\) 为输入，\(b\) 为偏移量。

对于特征集合，可以将模型表示为：

损失函数

常见的损失函数是平方误差 \(l^{(i)}(\mathbf{w}, b) = \dfrac{1}{2}(\hat{y}^{(i)} - y^{(i)})^2\). 常数 \(\frac{1}{2}\) 存在的意义是为了对损失函数求导后系数为 \(1\) .

反映到线性模型中，其在整个数据集上的损失均值为：

解析解

将 \(b\) 并入 \(\mathbf{w}\) 中，求解最小化 \(||\mathbf{y} - \mathbf{Xw}||^2\) 时参数的值，可以得到线性回归的解析解 \(\mathbf{w}^{\star} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}\).

一般只有简单问题的解析解才好求，因此解析解无法广泛地应用于深度学习之中。

随机梯度下降 SGD

直接求解析解往往效率低下，因此我们常训练模型以高效地求出近似解。

随机梯度下降法的思路是：

1. 初始化模型参数的值，比如随机初始化；

2. 每一步，沿当前点对应平均损失函数 \(L\) 的梯度方向，走给定步长长度。重复迭代多次。

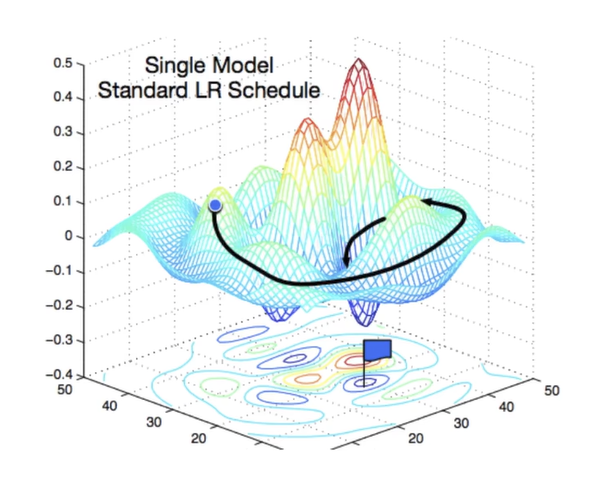
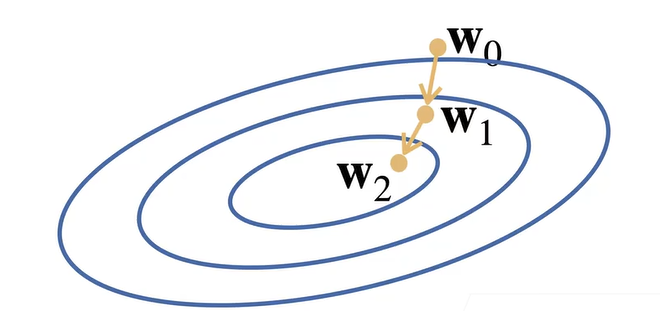
但裸梯度下降法每次求梯度的时候都需要遍历整个数据集，在数据集较大的情况下效率低下。因此有一个简单的优化是小批量随机梯度下降法：在选取损失函数时并不选择数据集所有样本的平均损失函数，而是从整个数据集中随机抽取小批量样本更新参数。

实现

例：从零开始实现线性回归 simp ver

%matplotlib inline
import random
from mxnet import autograd, np, npx  # autograd：MXNet 的自动求导引擎。
from d2l import mxnet as d2l

npx.set_np()

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = np.random.normal(0, 1, (num_examples, len(w)))  # 形状 (num_examples, len(w)) 的二维数组，元素服从标准正态分布。
    y = np.dot(X, w) + b  # 计算「无噪声」标签：y = X·w + b
    y += np.random.normal(0, 0.01, y.shape)  # 给标签加上一点均值为 0、标准差 0.01 的高斯噪声，使数据更真实。
    return X, y.reshape((-1, 1))  # 把 y reshape 成列向量 (num_examples, 1)，并返回 (X, y)。

true_w = np.array([2, -3.4])  # 定义「真实」权重和偏置，后面用来衡量模型学得好不好。
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)  # 调用上面函数，生成 1000 条样本；features 是 X，labels 是 y。

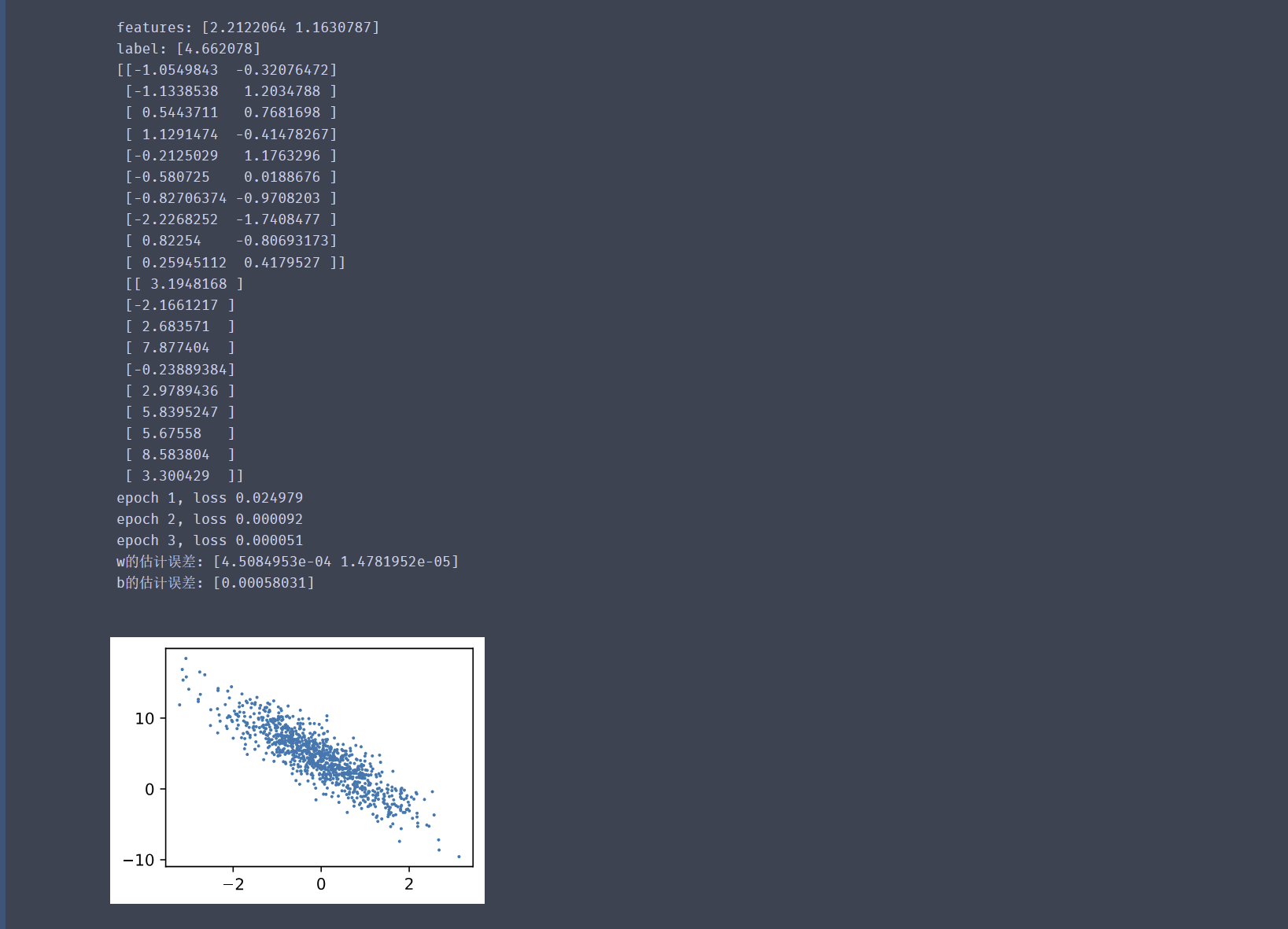
print('features:', features[0],'\nlabel:', labels[0])  # 看一下第一条数据长什么样，快速检查数据维度及数值范围。

d2l.set_figsize()  # d2l 包绘图相关设置
d2l.plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1);

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)  # 先把样本索引 [0, 1, 2, …, 999] 随机打乱，保证每个 epoch 顺序不同。
    for i in range(0, num_examples, batch_size):
        batch_indices = np.array(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]  # 每次循环返回一个小批量的 (X, y)，用 yield 做成生成器，节省内存。
        
batch_size = 10  # 设置批量大小。

for X, y in data_iter(batch_size, features, labels):  # 只迭代一次，打印第一个 batch 的 X 和 y，确认数据迭代器工作正常。
    print(X, '\n', y)
    break

w = np.random.normal(0, 0.01, (2, 1))  # 权重 w 初始化为形状 (2, 1) 的列向量，元素服从 N(0, 0.01²)。
b = np.zeros(1)  # 偏置初始化为 0。
w.attach_grad()  # 同 w.requires_grad_(True)
b.attach_grad()

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return np.dot(X, w) + b  # 这里 b 使用了广播机制

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    for param in params:
        param[:] = param - lr * param.grad / batch_size  # 手动实现 SGD：用当前梯度更新参数。param[:] 是原地赋值，防止创建新内存。
        
lr = 0.03  # 设置学习率、训练轮数，并把函数指针存到变量中，方便后面统一调用
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():  # 计算当前 batch 的预测值和损失。
            l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 计算l关于[w,b]的梯度
        l.backward()  # 反向传播，把损失对 w、b 的梯度写到 w.grad、b.grad。（在sgd函数内是 params.grad）
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    train_l = loss(net(features, w, b), labels)
    print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')  # 每轮结束后在整个训练集上计算一次平均损失，打印出来看是否下降。
    
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

例：使用 Gluon 实现线性回归 simp ver

from mxnet import autograd, gluon, np, npx  # gluon：高层神经网络 API
from d2l import mxnet as d2l

npx.set_np()

true_w = np.array([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)  # 按线性关系 y = X w + b + ε 随机生成 1000 条样本（同上）

def load_array(data_arrays, batch_size, is_train=True):  #@save
    # 把 NumPy/MXNet 数组封装成 Gluon 的数据迭代器
    dataset = gluon.data.ArrayDataset(*data_arrays)  # 把传进来的若干数组（这里是 features 和 labels）打包成一个 ArrayDataset 对象，方便后续按索引取用。
    return gluon.data.DataLoader(dataset, batch_size, shuffle=is_train)  # 再包一层 DataLoader，实现按批 (batch) 读取、打乱 (shuffle) 训练数据等功能，返回的 data_iter 可以 for X, y in data_iter 这样迭代。

batch_size = 10
data_iter = load_array((features, labels), batch_size)  # 用刚写的 load_array 把 features 和 labels 封装成迭代器

print(next(iter(data_iter)))  # 手动取一个批次的数据出来看看，验证封装是否正确。

# nn是神经网络的缩写
from mxnet.gluon import nn  # 从 mxnet.gluon 再导入子模块 nn，里面封装了层（Layer）和常用网络结构。

net = nn.Sequential()  # 实例化一个“顺序容器”网络；以后按添加顺序逐层前向传播。
net.add(nn.Dense(1))  # 向顺序容器里添加一个全连接层 Dense(1)

from mxnet import init  # 导入初始化器模块，用来给网络参数赋初值。

net.initialize(init.Normal(sigma=0.01))  # 把网络里的所有待训练参数按 均值为 0、标准差 0.01 的正态分布随机初始化。

loss = gluon.loss.L2Loss()  # 定义损失函数为 平方误差损失（L2Loss)

trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})
# 创建训练器：net.collect_params() 把网络中所有可训练参数收集起来；优化算法选用 'sgd'（随机梯度下降）；优化器超参仅设 learning_rate=0.03

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        with autograd.record():
            l = loss(net(X), y)
        l.backward()
        trainer.step(batch_size)  # 调用优化器，根据刚才算出的梯度更新一次参数。batch_size 用于把梯度除以批大小，实现平均。
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l.mean().asnumpy():f}')  # 打印当前 epoch 的编号以及平均损失值。.asnumpy() 把 MXNet NDArray 转成 NumPy 标量，方便 Python 格式化输出。
    
w = net[0].weight.data()  # 取出网络第 0 层（即我们添加的 Dense(1)）的权重参数。
print(f'w的估计误差： {true_w - w.reshape(true_w.shape)}')
b = net[0].bias.data()  # 取出网络第 0 层（即我们添加的 Dense(1)）的偏置参数
print(f'b的估计误差： {true_b - b}')

归一化指数函数回归 softmax regression

归一化指数函数

softmax 回归解决的是分类问题。具体的，对于 \(n\) 个特征输入及其对应权重，通过线性组合得到 \(m\) 个类别的权值：

得到的权值向量 \(\mathbf{o}\) 中的每个值代表样本是对应类别的可能值，其值越大样本是对应类别的可能性越大。

但是“可能值”并不易于量化，如果能转化成概率会更好比较。因此使用 softmax 函数：\(\mathbf{\hat{y}} = \operatorname{softmax}(\mathbf{o})\)，其中

这样得到的预测向量 \(\mathbf{\hat{y}}\) 中的每个值就代表样本是对应类别的概率（\(\hat{y_i} \in (0, 1)\) 且 \(\small\sum\limits_k y_k = 1\)），同时没有改变原有值的大小关系。

交叉熵损失

对于标签向量 \(\mathbf{y}\)（描述样本属于哪个/些类别，是1否0）和预测向量 \(\mathbf{\hat{y}}\)，其交叉熵损失函数定义为：

如果样本只属于至多一种类别（比如下例中的Fashion-MNIST数据集），则 \(\mathbf{y}\) 是独热的（只有一位是 \(1\)，剩余位全是 \(0\)），此时交叉熵损失可以简化为 \(L = - \log \hat{y_j}\) .

交叉熵损失常用于衡量两个概率之间的差异。原因之一是交叉熵损失的梯度为 \(\partial_{o_j} L(\mathbf{y}, \mathbf{\hat{y}}) = \hat{y_j} - y_j\)，这一值在概率较小的情况下较大，从而保证模型在训练后期仍然能保持足够的效率。

例： 从零开始实现softmax回归 simp ver

import torch
from IPython import display  # 用于在 Notebook 中动态刷新图表
from d2l import torch as d2l

batch_size = 256  # 每次送入网络的样本张数

import os, pathlib, torchvision
from torchvision import transforms
from torch.utils.data import DataLoader

data_dir = pathlib.Path.home() / 'Datasets' / 'FashionMNIST'  # 数据集保存路径
trans = transforms.ToTensor()

mnist_train = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=True,  transform=trans, download=True)  # 训练集：root 指定目录，train=True 表示训练集，download=True 会自动下载
mnist_test  = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=False, transform=trans, download=True)  # 测试集：train=False

train_iter = DataLoader(mnist_train, batch_size=256, shuffle=True)
test_iter  = DataLoader(mnist_test,  batch_size=256, shuffle=False)

num_inputs = 784  # 每张图片 28×28=784 个像素作为输入特征 (n=784)
num_outputs = 10  # Fashion-MNIST 共 10 类 (m=10)

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)  # 权重矩阵：784×10，正态初始化 N(0,0.01)，自动求导
b = torch.zeros(num_outputs, requires_grad=True)  # 偏置向量：长度为 10，初始化为 0

def softmax(X):
    X_exp = torch.exp(X)  # 对每个元素做 e^x
    partition = X_exp.sum(1, keepdim=True)  # 每行求和，得到归一化因子
    return X_exp / partition  # 这里应用了广播机制：每行除以该行总和

def net(X):
	# X 原始形状 (batch,1,28,28)，先 reshape 成 (batch,784)，再与 W 做矩阵乘法，加偏置 b，最后过 softmax
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])    # 交叉熵损失

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y  # 布尔张量：True 表示预测正确
    return float(cmp.type(y.dtype).sum())  # 把 True 转 1 后求和

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():  # 不计算梯度，减少内存/加速
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())  # 累加
    return metric[0] / metric[1]  # 返回准确率

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]
    
evaluate_accuracy(net, test_iter)

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    metric = Accumulator(3)   # 分别累加「损失和」「正确数」「样本数」
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)  # y_hat[i, k] 代表第 i 张图片被模型判定为类别 k 的概率。
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()  # 对平均损失求梯度
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()  # 使用 d2l.sgd 自定义批量梯度下降
            updater(X.shape[0])  # 传入批量大小，更新 W,b
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]  # 返回平均损失、平均准确率

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):  # 初始化坐标轴、线型、图例等
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):  # 每调用一次把新点画到图上
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)  # 在 Notebook 中实时刷新
        display.clear_output(wait=True)

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])  # 创建画布
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)  # 训练一个 epoch
        test_acc = evaluate_accuracy(net, test_iter)  # 评估测试集
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
	# 训练完做断言，确保指标合理
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

lr = 0.05  # 学习率

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)  # 使用 d2l 封装的随机梯度下降，对 [W,b] 做更新

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)  # 数字 -> 文本标签
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)  # 显示 6 张图及真实/预测标签

例：softmax 回归的简洁实现 simp ver

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256

import os, pathlib, torchvision
from torchvision import transforms
from torch.utils.data import DataLoader

data_dir = pathlib.Path.home() / 'Datasets' / 'FashionMNIST'
trans = transforms.ToTensor()

mnist_train = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=True,  transform=trans, download=True)
mnist_test  = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=False, transform=trans, download=True)

train_iter = DataLoader(mnist_train, batch_size=256, shuffle=True)
test_iter  = DataLoader(mnist_test,  batch_size=256, shuffle=False)

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))  # 定义网络
# nn.Flatten()：把张量中除第 0 维（batch 维）以外的所有维拉成一条长向量。在 softmax 回归里，它把 (B, 1, 28, 28) 变成 (B, 784)，方便后面全连接层接收。
# nn.Linear(in_features, out_features)：全连接（仿射变换）。y = xWᵀ + b其中 x 是 (batch, in_features)，W 是 (out_features, in_features)，b 是 (out_features,)，输出 y 为 (batch, out_features)。

def init_weights(m): # 定义一个回调函数，当遍历到某层 m 是 nn.Linear 时，把 m.weight 用 均值为 0、标准差 0.01 的正态分布重新初始化；偏置 bias 默认初始化为 0。
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);  # 递归地对 net 内部所有子模块调用 init_weights，实现权重初始化。

loss = nn.CrossEntropyLoss(reduction='none')
# nn.CrossEntropyLoss 内部先对网络输出做 softmax，再计算负对数似然。
# reduction='none' 表示 不 做平均/求和，返回每个样本的 loss（shape (batch_size,)），方便后续手动调权。

trainer = torch.optim.SGD(net.parameters(), lr=0.1)  # 定义优化器：使用 随机梯度下降 (SGD)，学习率 0.1。
# net.parameters() 返回所有待训练张量（权重、偏置）。

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

常见评价模型训练好坏的参数：

精确率 precision：\(\text{pre} = \dfrac{\text{TP}}{\text{TP} + \text{FP}}\)

召回率 recall：\(\text{rec} = \dfrac{\text{TP}}{\text{TP} + \text{FN}}\)

F1值：\(\text{F1} = \dfrac{2 \times \text{pre} \times \text{rec}}{\text{pre} + \text{rec}}\)

深度神经网络

多层感知机 Multilayer Perceptron

感知机

感知机用于解决二分类问题：对于空间中的若干两种颜色的点，需要找到一组 \(\mathbf{w}, b\)，构成超平面 \(\mathbf{w x} + b = 0\) 将两种颜色的点恰分隔在平面两侧。（假设总存在至少一个超平面可以满足要求）

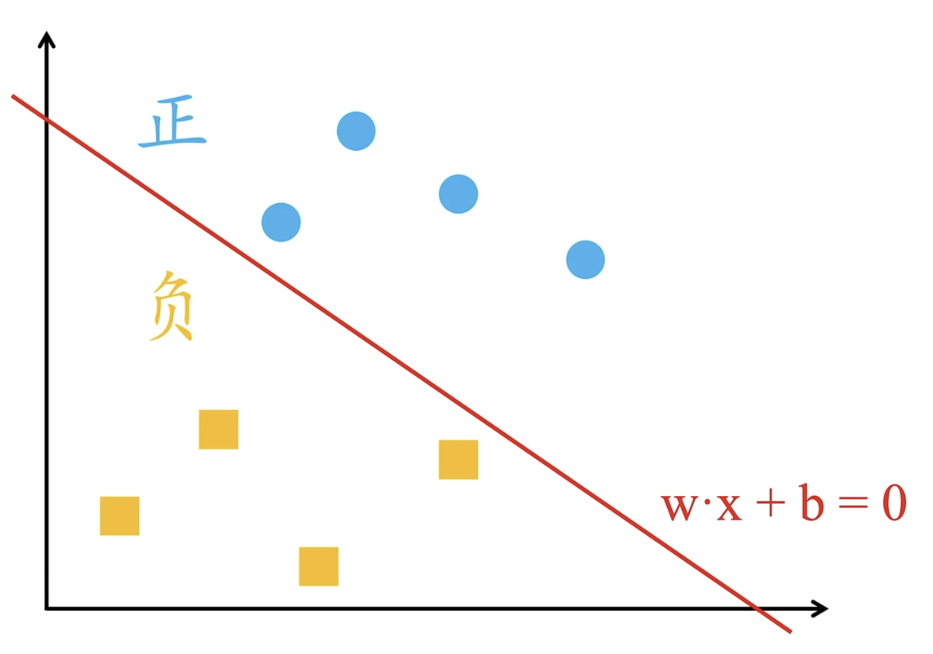
感知机的激活函数选择为取符号函数 \(\operatorname{sgn}(x) = \dfrac{x}{|x|}\)。具体地，感知机的方程为 \(y = \begin{cases} 1 &, \mathbf{wx} + b > 0 \\ -1 &, \mathbf{wx} + b \le 0 \end{cases}\) （等号可任意归类。当然，这是细枝末节）。而损失函数则由分类错误的点到分割面的距离之和决定，即 \(d = \dfrac{1}{\| \mathbf{w} \|}|\mathbf{w} \cdot \mathbf{x_0} + b|\) 。进一步考虑拆掉绝对值，发现 \(d = \dfrac{1}{\| \mathbf{w} \|}( -y_0 (\mathbf{w} \cdot \mathbf{x_0} + b))\) 。而实际上感知机只需要完成分类任务，不关注分割面是否“比较居中”地分离了二者，因此每个点到分割面的距离大小并不是感知机关注的重点，故删去距离公式中的范数因子，最终得到的损失函数为 \(l = - \sum\limits_{x_i \in M_e} y_i (\mathbf{w} \cdot \mathbf{x_i} + b)\)，其中 \(M_e\) 表示分类错误的点的集合。

实际上，在感知机被发明的那个年代，训练模型的手段还比较落后。当时选择的手段是一个一个点迭代（当时的人们还没有意识到梯度下降法），思路如下：

从现在的角度看，感知机的训练手段其实就是使用批量大小为 1 的梯度下降法，而损失函数则为 \(L(y, \mathbf{x}, \mathbf{w}) = \operatorname{ReLU}(-y \langle \mathbf{w}, \mathbf{x} \rangle)\) 。

多层感知机

感知机只能解决二分类问题，但现实中大部分分类问题不只两层（比如异或，这是一个二元输入一元输出四分类问题）。因此使用多层感知机来实现更复杂的分类问题。

相比线性神经网络，多层感知机在输入层和输出层之间添加了若干隐藏层，实现从线性问题到非线性问题。简单起见，我们先考虑只有一层隐藏层的多层感知机。

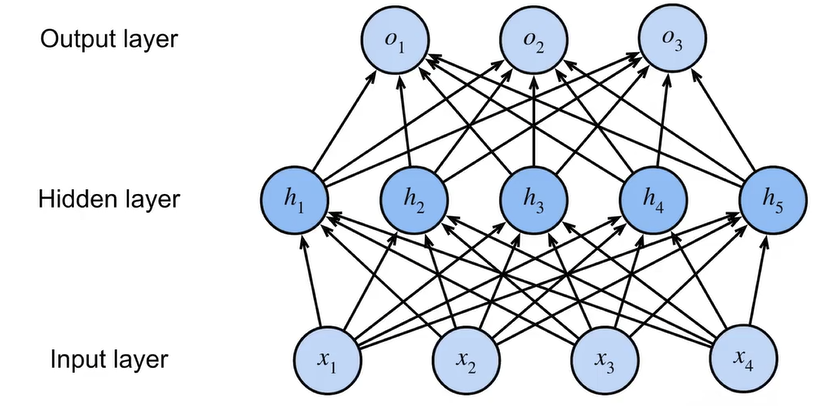
该多层感知机的变换公式如下：

其中 \(\sigma(\mathbf{X})\) 被称为激活函数，用于压缩输出，以拟合复杂的函数（如果不加激活函数，多层感知机将退化为线性模型）。激活函数往往是非线性的逐元素函数。以下给出若干常见的激活函数：

• ReLU 函数

  \[\operatorname{ReLU}(x) = \max(x, 0) \]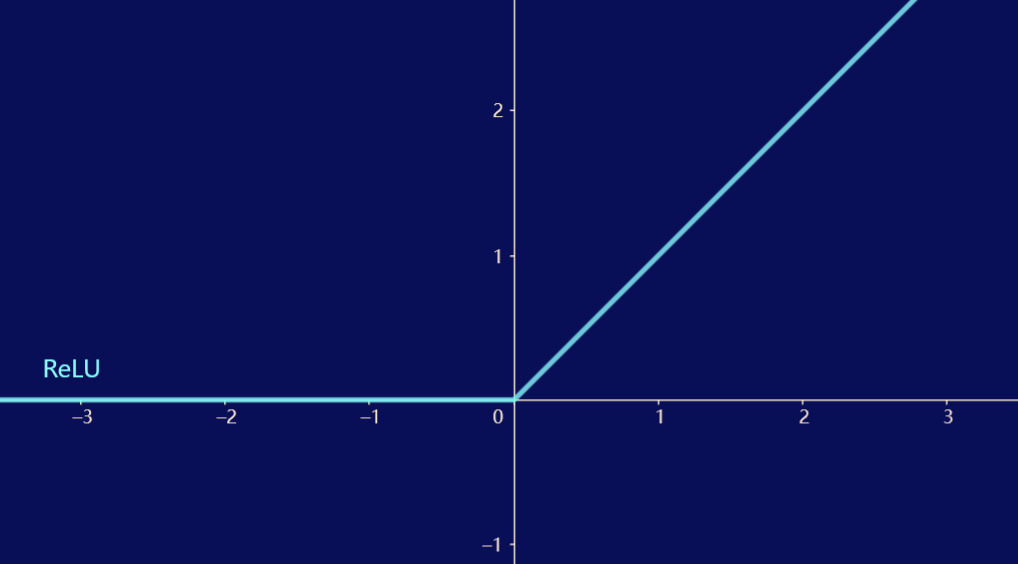

  
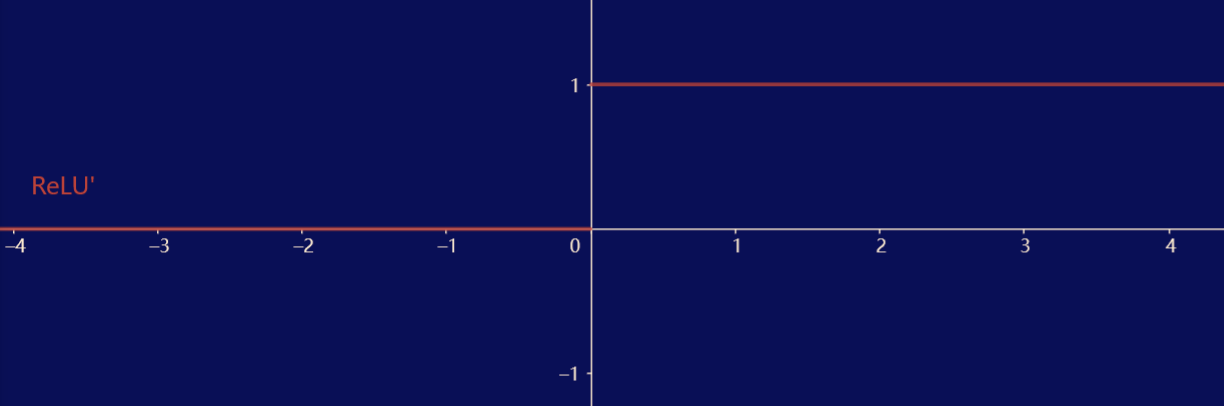
  ReLU 函数仅保留正元素而丢弃所有负元素，呈分段线性状态。ReLU 函数的导数在负输入时为 \(0\)，而在正输入时为 \(1\)，并规定输入为 0 时 ReLU 函数的导数取 \(0\)，从而实现较好的求导表现。

• sigmoid 函数

  \[\operatorname{sigmoid}(x) = \dfrac{1}{1 + e^{-x}} \]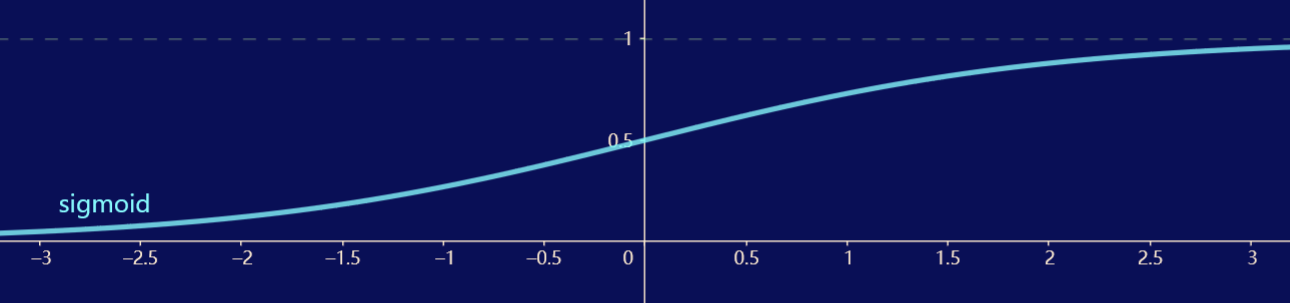

  
  sigmoid 函数是一个平滑可微的值域为 \((0, 1)\) 的激活函数，常用于在输出是分类问题的概率时作为输出单元上的激活函数。sigmoid 函数的导数是单峰函数，在 0 处取得最大值 \(0.25\)，离 0 越远取值越接近 \(0\)。

• tanh 函数

  \[\operatorname{tanh}(x) = \dfrac{1 - e^{-2x}}{1 + e^{-2x}} \]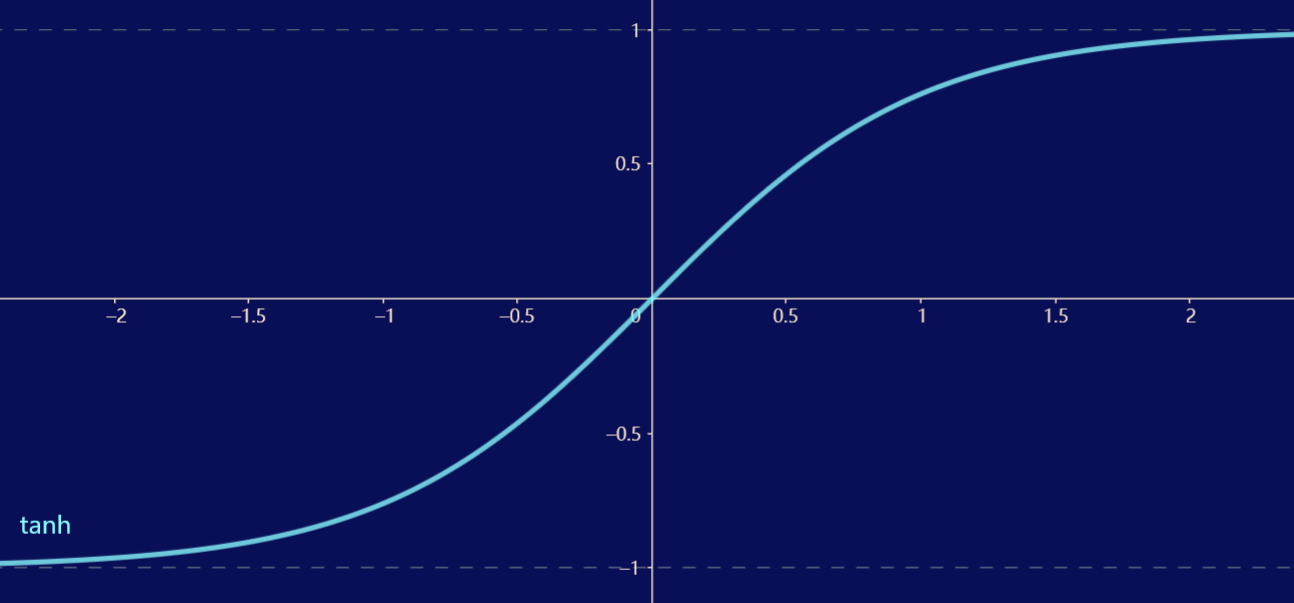

  
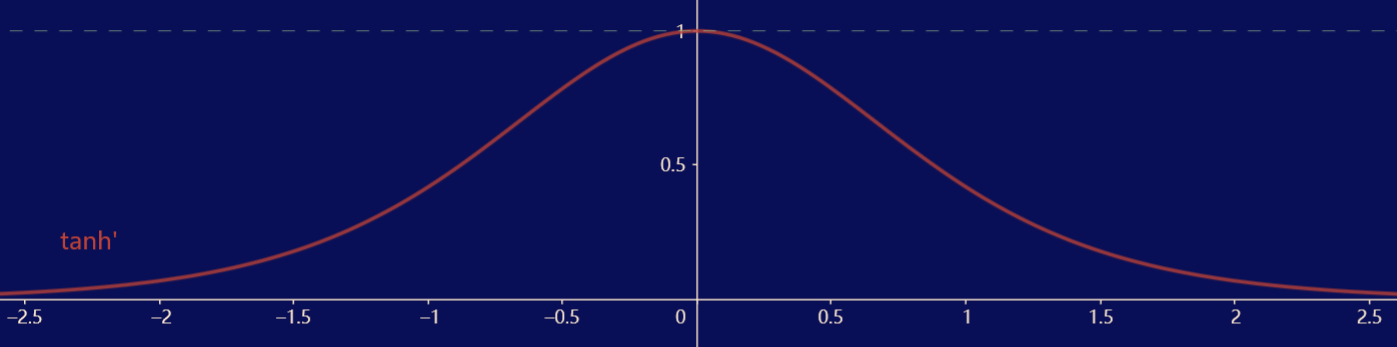
  tanh 函数是一个平滑可微的值域为 \((-1, 1)\) 的激活函数，不同于 sigmoid 函数，tanh 函数关于原点对称。tanh 函数的导数是单峰函数，在 0 处取得最大值 \(1\)，离 0 越远取值越接近 \(0\)。

例：从零开始实现多层感知机 simp ver

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256

import os, pathlib, torchvision
from torchvision import transforms
from torch.utils.data import DataLoader

data_dir = pathlib.Path.home() / 'Datasets' / 'FashionMNIST'
trans = transforms.ToTensor()

mnist_train = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=True,  transform=trans, download=True)
mnist_test  = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=False, transform=trans, download=True)

train_iter = DataLoader(mnist_train, batch_size=256, shuffle=True)
test_iter  = DataLoader(mnist_test,  batch_size=256, shuffle=False)

num_inputs, num_outputs, num_hiddens = 784, 10, 256  # 输入层、输出层、隐藏层节点个数

# 初始化参数
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))  

params = [W1, b1, W2, b2]  # 收集所有待优化参数，后面传给 torch.optim.SGD

def relu(X):
    a = torch.zeros_like(X)  # zeros_like 生成和 X 形状相同的全 0 张量，避免显式写形状。
    return torch.max(X, a)

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # @ 是 Python 3.5+ 的矩阵乘运算符
    return (H@W2 + b2)  # 广播机制会把 (256,) 的 b1 自动扩展到 (batch,256)；

loss = nn.CrossEntropyLoss(reduction='none')  # 多类别交叉熵，接收 logits 和类别索引.reduction='none' 返回每个样本的 loss，便于后续自定义求平均或加权

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)  # updater 是一个 SGD 优化器，后续 updater.step() 做参数更新。
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)  # 封装好的训练循环：

d2l.predict_ch3(net, test_iter)  # d2l.predict_ch3(net, test_iter)

例：多层感知机的简洁实现 simp ver

import torch
from torch import nn
from d2l import torch as d2l

import os, pathlib, torchvision
from torchvision import transforms
from torch.utils.data import DataLoader

data_dir = pathlib.Path.home() / 'Datasets' / 'FashionMNIST'
trans = transforms.ToTensor()

mnist_train = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=True,  transform=trans, download=True)
mnist_test  = torchvision.datasets.FashionMNIST(
    root=str(data_dir), train=False, transform=trans, download=True)

train_iter = DataLoader(mnist_train, batch_size=256, shuffle=True)
test_iter  = DataLoader(mnist_test,  batch_size=256, shuffle=False)

batch_size, lr, num_epochs = 256, 0.1, 10

net = nn.Sequential(nn.Flatten(),  # 输入层，展平用
                    nn.Linear(784, 256),  # 隐藏层
                    nn.ReLU(),  # 隐藏层的激活函数
                    nn.Linear(256, 10))  # 输出层

def init_weights(m):
    if type(m) == nn.Linear:  # 如果是 Linear 层，就用正态分布初始化权重，标准差 0.01
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

模型拟合 model fitting

误差

• 训练误差：模型在训练集上的误差。

• 泛化误差：模型在从原始样本的分布中抽取无限多数据样本时的误差。

• 验证误差：模型在验证集上的误差。

原则上，在确定所有超参数之前，模型不应接触测试集。因此需要用验证集来判断模型的拟合程度，即用验证误差去估计泛化误差。当训练数据稀缺时，常用 K折交叉验证 来处理这一问题：将原始训练数据随机均分为 \(K\) 份，每次实验在 \(K - 1\) 个子集上进行训练，并在剩余的 \(1\) 个子集上进行验证。最后将 \(K\) 次实验的结果取平均来估计误差。

拟合

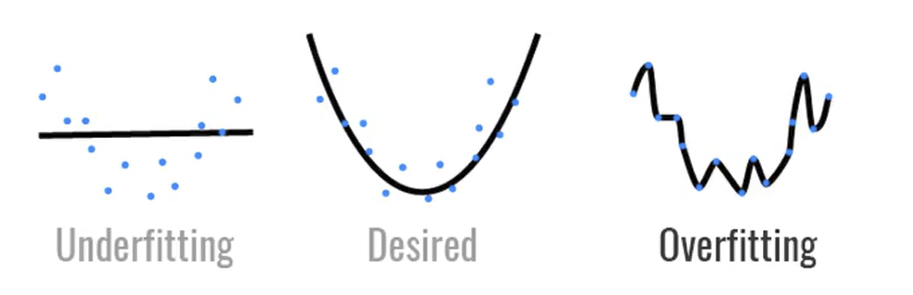
• 欠拟合：训练误差和验证误差都很大，模型容量小于数据复杂度。
  对于欠拟合，模型无法减小训练误差（表达力不足），我们有理由相信可以用一个更复杂的模型减小训练误差。

• 过拟合：训练误差远小于验证误差，模型容量大于数据复杂度。
  对于过拟合，模型往往只“记住”训练集的数据，而没有“理解”其背后的规律。高容量的模型由于其自身的灵活性，容易产生过拟合现象。但验证误差和训练误差之间的差距较大并不总是一件坏事，在深度学习领域，即使是最好的预测模型在训练集上的表现往往比在验证集上好，因此我们通常关心训练误差，而非二者间的差距。
  解决过拟合的技术被称为正则化。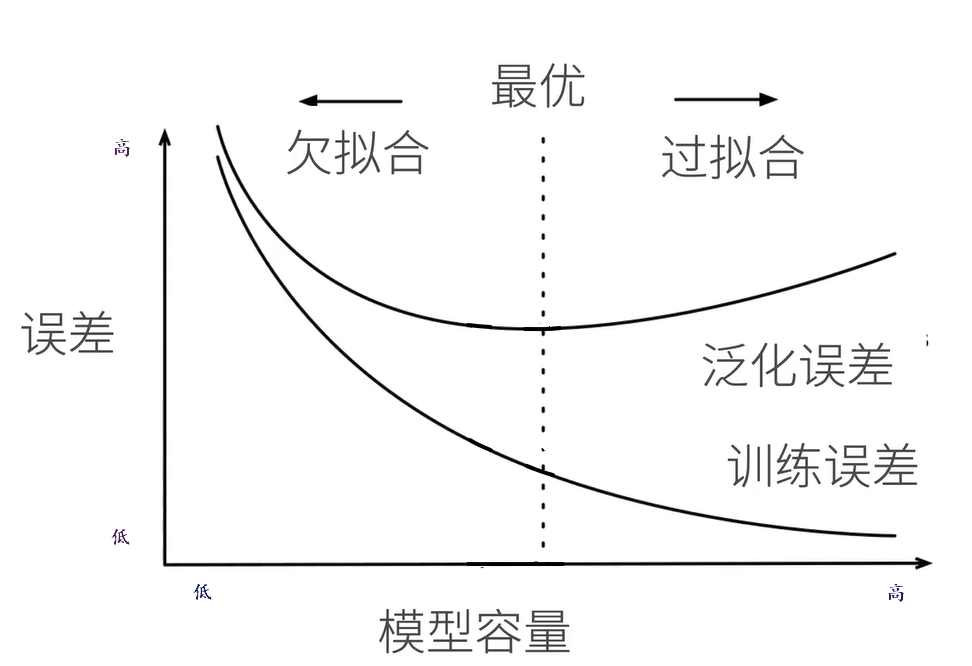

  

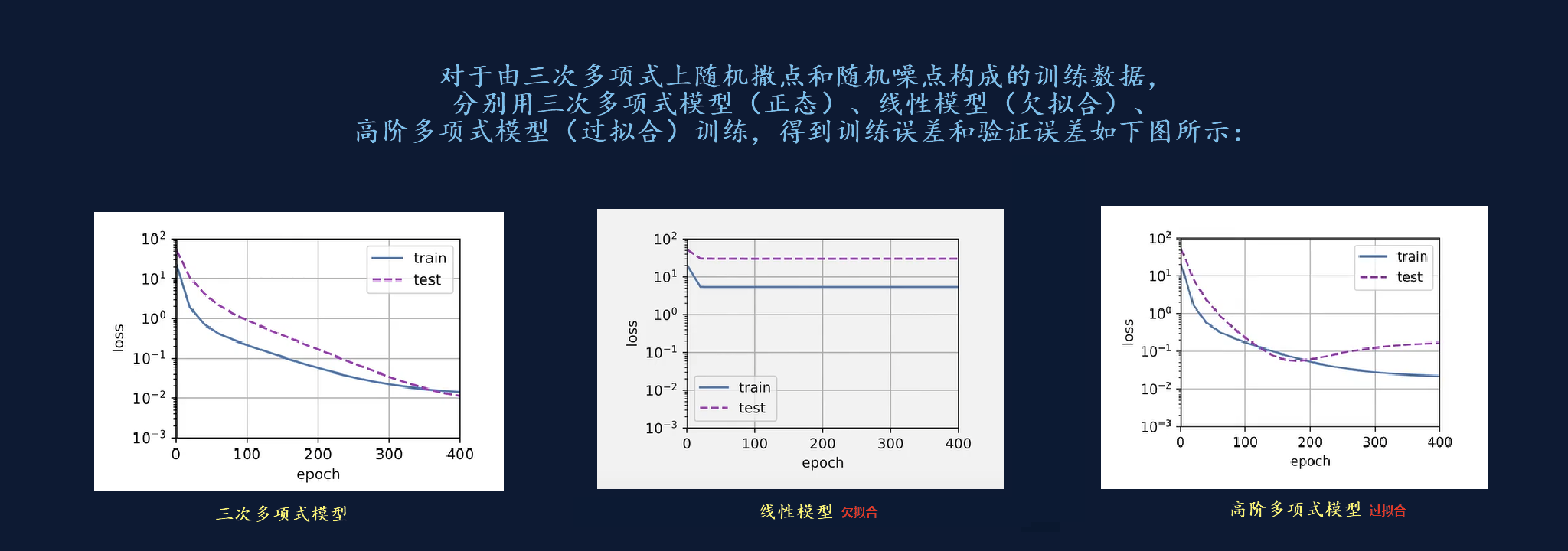
权重衰退法 weight decay

以线性模型 \(\mathbf{\hat{y}} = \mathbf{Xw} + \mathbf{b}\) 为例。权重衰退法解决过拟合的思路是避免产生过大的 \(w\)，具体地，模型在限制损失函数 \(l(\mathbf{w}, b) = \dfrac{1}{n} l^{(i)}(\mathbf{w}, b) = \dfrac{1}{n} \sum\limits_{i=1}^{n}\dfrac{1}{2}(\mathbf{w}^T\mathbf{x}^{(i)}+b-y^{(i)})^2\) 最小时也需要保证 \(|| w || ^2 \le \theta\).

可以证明，对于每个 \(\theta\)，都可以找到一个 \(\lambda\) 使得之前的两条限制等价于令下面的总损失函数最小：

原本的 \(w\) 的迭代方程为 \(w_{t+1} = w_{t} - \eta \dfrac{\partial l(w_t, b_t)}{\partial w_t}\)，而权重衰退法的迭代方程为 \(w_{t+1} = (1 - \eta \lambda)w_{t} - \eta \dfrac{\partial l(w_t, b_t)}{\partial w_t}\). 通常情况下 \(0 < \eta \lambda < 1\)，从而使 \(w_{t}\) 这一项在迭代时产生的作用变小，实现约束 \(w\) 大小的目的。

暂退法 dropout

暂退法通过在前向传播时随机删除部分节点实现正则化。暂退法的中心思想是给每一层注入无偏差（期望不变）的噪声，具体地，dropout 函数会使中间激活值进行以下操作：

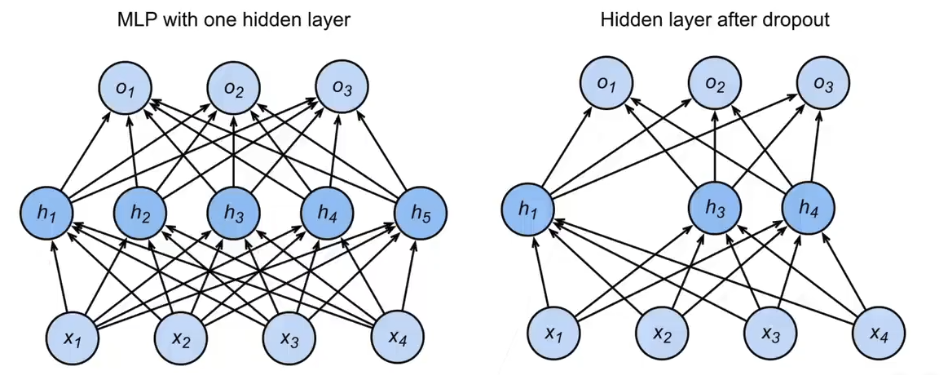
例如，对于单隐藏层的网络：

使用暂退法后变为：

对于这个隐藏层，部分节点被随机删除，而整个层元素的期望值不变。一种理解方式是，暂退法相当于同时训练了 \(2^m\) 个“子网络”（\(m\) 是进行暂退法的层的元素个数之和），最后做模型平均，减小泛化误差。

卷积神经网络 Convolutional Neural Network

卷积层

考虑现在需要在一张彩色二维图像上识别目标，使用多层感知机的思路会列出如下公式：

但是多层感知机使用全连接层，对于图片这种数据量较大的输入会产生极多的参数，模型无法承受，因此需要优化上述公式。

平移不变性

平移不变性的原理是：输出不应因为检测目标出现在输入图像的位置变化而不同。换言之，\(U\) 和 \(V\) 与 \(i,j\) 无关，因此公式可以简化为：

局部性

局部性的原理是：检测目标应当集中于输入图像的一部分。换言之，计算 \(H_{i,j}\) 时不应考虑距离 \((i,j)\) 很远的地方，因此公式可以化简为：

化简到这一步参数较全连接层已经极大简化。我们称这样的层为卷积层，称 \(V\) 为卷积核。与全连接层对比，\(V\) 就是卷积层的参数。

手动设置卷积核

卷积核虽然小，但能做的事情很多。以图像边缘检测为例:

假设有如下黑白图像，中间是黑色（0），两侧是白色（1），共两条纵向边缘。

tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])

利用 \(1 \times 2\) 卷积核 tensor([[1.0, -1.0]]) （实操卷积核应该是正方形，此处仅作演示）与该图像做卷积，得到如下结果：

tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

可以看到检测到两条纵向边界，其中 1 代表从白色到黑色的边缘，-1 代表从黑色到白色的边缘。

学习卷积核

对于更复杂的情况，我们需要学习卷积核。这一操作与全连接层的模型学习是类似的。

例：简单卷积核的学习 simp ver

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

X = torch.ones((6, 8))
X[:, 2:6] = 0  # X 是6行8列的黑白图像，其中最左两列和最右两列是1（白），中间四列是0（黑）

K = torch.tensor([[1.0, -1.0]])  # K 是上例中的竖直边缘检测核，K不会直接参与训练，我们的目标是让卷积核的学习结果与其相近

Y = corr2d(X, K)  # Y 是 X 和 K 的卷积结果，用于训练

conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)  # 输入通道、输出通道、核大小、忽略偏置

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):  # 训练10轮
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

conv2d.weight.data.reshape((1, 2))  # 输出结果。实测为 tensor([[ 0.9508, -1.0260]])，与原本的 K 相近

多通道

实际上图片并非二维的，还会有第三通道表示RGB等（多输入通道），以及我们有时需要对同一输入产生多种不同的输出（多输出通道），因此我们需要将公式修改为：

具体处理时，卷积层对每个通道设置对应卷积核进行卷积操作，最后将这 \(c\) 个卷积后的结果加起来进行汇总。对于多输出通道，每个通道均执行一次上述操作，注意同一输入通道的卷积核对于不同的输出通道是不同的，最后得到 \(d\) 个结果，将其叠放（stack）得到一个三维张量结果。

池化层

池化的思想是将原输入的局部合并成一个点。常用的池化方法有两种，一种是最大池化，一种是平均池化。具体操作的时候设置一个 \(p \times q\) 的窗口遍历每一个位置，得到最后的输出。

\(p\) 和 \(q\) 一般不会很大，步长设置与窗口长宽相同。

池化删去了输入中的很多点（比如设置 \(2 \times 2\) 的窗口输出就只有原图的\(\frac{1}{4}\)），但其信息丢失并不多。在过去池化往往被用于内存减负，现在结合上卷积层，池化操作可以明显扩大感受野，等价于用更大核却不增加参数，是非常优雅的操作。

残差连接

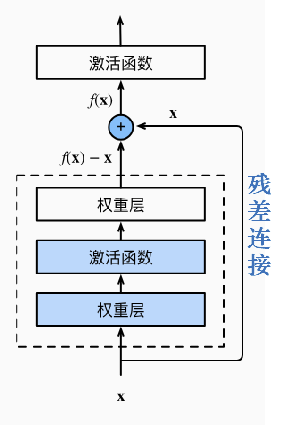
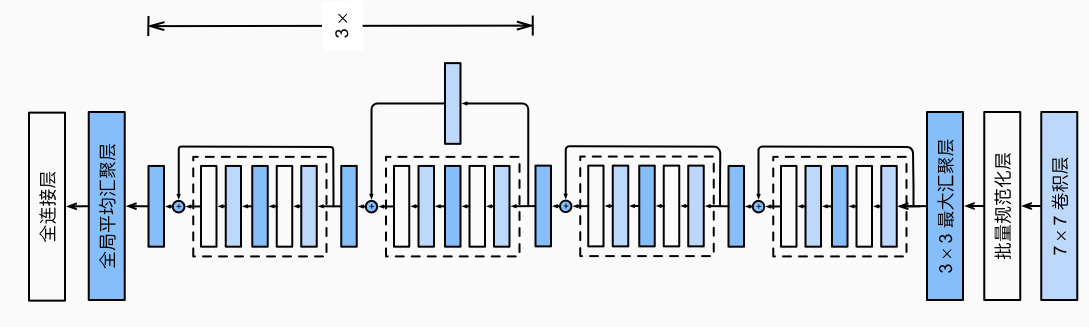
残差连接是ResNet的独特操作。在神经网络层数很深时，参数可能难以学习（网络退化），残差连接通过将之前浅层训练的结果跳跃地传入深层，并将训练函数减去连接的值。这样在最坏的情况下，如果被越过的部分已经难以学习，那么无非就是这一部分没有贡献，而连接的值继续前向传播，不会影响后面的运算。这样，神经网络可以做得很深而无需担心训练困难的问题。

注意力机制 Attention Mechanism

query, key, value

在生物学中有两种注意力机制，一种是由于环境中某物体具有特殊性质，我们非自主地注意到它；另一种是由于想找到具有某些特点的物体，我们自主地注意到它。

视觉变换器 Vision Transformer (ViT)

图神经网络 Graph Neural Network

GNN 一开始被用于解决图上的深度学习问题（比如社交网络，节点是用户，边表示用户间的关联性）。在计算机视觉对GNN的应用中，我们将每个像素点（或每个像素块patch）视作一个节点，连边则由节点之间的相似度（距离）决定，比如对于两个节点各自的特征向量，计算其余弦相似度决定边的连接（有无、方向、权值等）。每次更新的时候更新节点的权值，由其原有权值和邻居决定。

变换器 Transformer

变换器一开始被应用于语言模型上。