Brooks 定理

对于简单连通图 G，若 G 既不是完全图，也不是奇回路，则 \(\chi(G) \le \delta(G)\)；否则有 \(\chi(G) = \delta(G) + 1\) 。其中 \(\chi(G)\) 是 G 的最小点正常着色数，\(\delta(G)\) 是 G 的最大点度数。

证明

记 \(k = \delta(G)\) 。易知 \(k = 1\) 和 \(k = 2\) 的时候命题成立，以下讨论针对 \(k \ge 3\) 的情况。

Lemma1：若按一种顺序标记图 G 中的所有节点 \(v_1, v_2, \dots, v_n\)，满足 \(\forall i \le n\)，在 \(v_1, v_2, \dots, v_{i-1}\) 至多有 \(k-1\) 个点与 \(v_i\) 相邻，则 \(\chi(G) \le \delta(G)\) 。

正确性是显然的。

• Case 1：若 G 不是 k-正则图。
  则必然存在一个节点的度数小于 \(k\)，钦定它为 \(v_n\) 。从 \(v_n\) 开始bfs遍历整张图，按照遍历顺序倒序标号 \(v_{n-1}, v_{n-2}, \dots, v_1\)。
  由于 \(\forall i, d(i) \le k\)，且除了 \(v_n\) 之外所有的节点总有至少一个编号更高的节点在该节点到 \(v_n\) 的路径上。故 \(\forall i \le n-1\)，在 \(v_1, v_2, \dots, v_{i-1}\) 至多有 \(k-1\) 个点与 \(v_i\) 相邻，而 \(d(v_n)\) 本来就小于 \(k\)，自然更满足上述条件，故由引理1可知 \(\chi(G) \le \delta(G)\)。

• Case 2：若 G 是 k-正则图。
  即 \(d(v_1) = d(v_2) = \dots = d(v_n) = k\) 。

  • Case 2-1：若 G 中有割点。
    挑出其中一个割点 \(x\) 。割去 \(x\) 后得到若干连通块 \(C_1, C_2, \dots C_m\)，其中 \(m \ge 2\) 。
    注意到 \(\forall j, C_j \or x\) 的点导出子图不是 k-正则图（在各导出子图中 \(d(x)\) 必然小于 \(k\)），故 \(C_j \or x\) 的点导出子图 是可 \(k\) 点正常着色的。而每个 \(C_j \or x\) 的点导出子图 染色独立，总可以将 \(x\) 的染色相同。故所有的点导出子图之并（图G）也是可 \(k\) 点正常着色的。

  • Case 2-2：若 G 中没有割点。
    考虑若存在这样一个点 \(v_n\)，其有两个不相邻的邻点 \(v_1, v_2\)，且 \(G - \{ v_1, v_2 \}\) 连通。那么在 \(G - \{ v_1, v_2 \}\) 上从 \(v_n\) 开始bfs遍历，按照遍历顺序倒序标号 \(v_{n-1}, v_{n-2}, \dots, v_4, v_3\) 。由于 \(v_1, v_2\) 不相邻，所以可以钦定 \(v_1, v_2\) 染同一种颜色。\(v_3\) 至 \(v_{n-1}\) 节点满足引理1。而 \(v_n\) 虽然有 \(k\) 个邻点，但其中两个邻点 \(v_1, v_2\) 是同色的，故 \(v_n\) 的邻点可以用至多 \(k-1\) 种颜色染色。于是所有的点满足引理1的条件，整张图 G 是可 \(k\) 点正常着色的。
    所以问题变成找到这样一组 \(\{ v_n, v_1, v_2 \}\) 点对。

    在图 G 中任取一点 \(x\)，考虑图 \(G - \{ x \}\)：

    • Case 2-2-1：若 \(G - \{ x \}\) 中没有割点。
      则必然存在一个节点 \(y\) 满足 \(\operatorname{dis}(x, y) = 2\) （不可能所有点到 \(x\) 的距离都是 \(1\)，那就是完全图了。如果能找到一个距离大于 \(2\) 的点那么一定在路径上存在有一个距离等于 \(2\) 的点）。令 \(v_1 = x, v_2 = y\)，\(v_n\) 取 \(x\) 和 \(y\) 最短路径上经过的那个点。
      显然 \(v_n\) 与 \(v_1, v_2\) 相邻，\(v_1\) 和 \(v_2\) 不相邻。由于 \(G - \{ x \}\) 中没有割点，故 \(G - {x, y}\) 依然连通。由此得知 G 可 \(k\) 点正常着色。
    • Case 2-2-2：若 \(G - \{ x \}\) 中有割点。
      考察 \(G - \{ x \}\)（这是一个连通图）的简单圆方树：方点至少有 \(2\) 个。因为如果只有一个那么 \(G - \{ x \}\) 中没有割点。
      故至少有 \(2\) 个叶子方点，且 \(x\) 与这两个方点表示的点双中的非割点的点相连。否则这个方点在 \(G - {x}\) 中的割点也会成为 \(G\) 的割点。
      令 \(v_n = x\)，\(v_1, v_2\) 分别是两个叶子方点表示的点双中与 \(x\) 相连的非割点的点。
      显然 \(v_n\) 与 \(v_1, v_2\) 相邻。若 \(v_1\) 与 \(v_2\) 相邻，那么由于 \(v_1\) 和 \(v_2\) 所在的点双在经过 \(G - \{ x \}\) 中的割点还有一条路径，那么说明 \(v_1\) 与 \(v_2\) 属于同一个点双，与假设不符，即 \(v_1\) 与 \(v_2\) 不相邻。
      在 \(G - \{ x \}\) 中，由于 \(v_1, v_2\) 是分属不同点双的非割点，因此删去二点不影响连通性，即 \(G - \{ x, v_1, v_2 \}\) 是连通图。而 \(d(x)=k, k \ge 3\)，故 \(x\) 除了 \(v_1, v_2\) 还有别的相邻的点，故 \(G - \{ v_1, v_2 \}\) 是连通图。
      综上 G 是可 \(k\) 点正常着色的。

圆方树

以下讨论针对 \(n \ge 2\) 的简单连通图。

点双连通图：图中任意两不同点之间都有至少两条点不重复的路径。（注：对于 \(n \ge 3\) 的情况，该定义等价于没有割点的图。特别的，对于 \(n = 2\) 的简单连通图，其是一个点双连通图）

点双连通分量：图的极大点双连通子图。

圆方树：原图中的每个点对应树中的圆点，原图中每个点双对应树中的方点。方点与圆点之间有边当且仅当原图中圆点对应的点属于方点对应的点双。

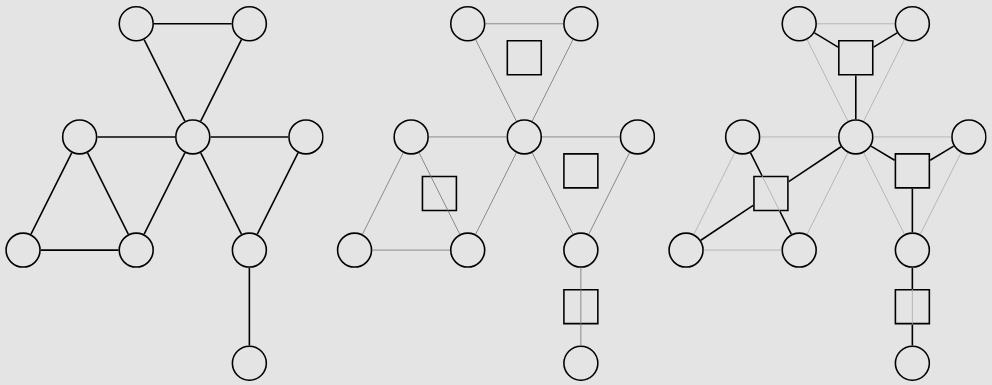
简单圆方树：圆方树删去叶子圆节点的子树。

圆方树的性质

1. 仅存在方点和圆点之间的边，不存在同种点之间的边。换言之，圆方树是一个二分图。

2. 一个点在原图中是割点当且仅当其在圆方树中是非叶圆节点。（注：圆方树视作无根树，也就是说这里的叶子指的是度数为 \(1\) 的节点）

3. 简单圆方树中方点的度数代表其对应点双在原图中包含多少个割点。