吴恩达深度学习课程五：自然语言处理 第三周：序列模型与注意力机制（二）束搜索

此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第五课第三周的内容，3.2到3.5的内容。

---

本周为第五课的第三周内容，与 CV 相对应的，这一课所有内容的中心只有一个：自然语言处理（Natural Language Processing，NLP）。
应用在深度学习里，它是专门用来进行文本与序列信息建模的模型和技术，本质上是在全连接网络与统计语言模型基础上的一次“结构化特化”，也是人工智能中最贴近人类思维表达方式的重要研究方向之一。
这一整节课同样涉及大量需要反复消化的内容，横跨机器学习、概率统计、线性代数以及语言学直觉。
语言不像图像那样“直观可见”，更多是抽象符号与上下文关系的组合，因此理解门槛反而更高。
因此，我同样会尽量补足必要的背景知识，尽可能用比喻和实例降低理解难度。
本周的内容关于序列模型和注意力机制，这里的序列模型其实是指多对多非等长模型，这类模型往往更加复杂，其应用领域也更加贴近工业和实际，自然也会衍生相关的模型和技术。而注意力机制则让模型在长序列中学会主动分配信息权重，而不是被动地一路传递。二者结合，为 Transformer 等现代架构奠定了基础。

本篇的内容关于束搜索，是在 seq2seq 模型中用于推理阶段的解码策略。

1. 序列生成的实质：条件概率

在开始束搜索之前，一个关键问题是： seq2seq 模型在“生成序列”时，本质上到底在做什么？
答案是：序列生成，本质上是在建模并求解一个条件概率最大化问题。
这是整个模型逻辑的核心，我们来具体展开：

1.1 模型输出：条件概率最大的序列

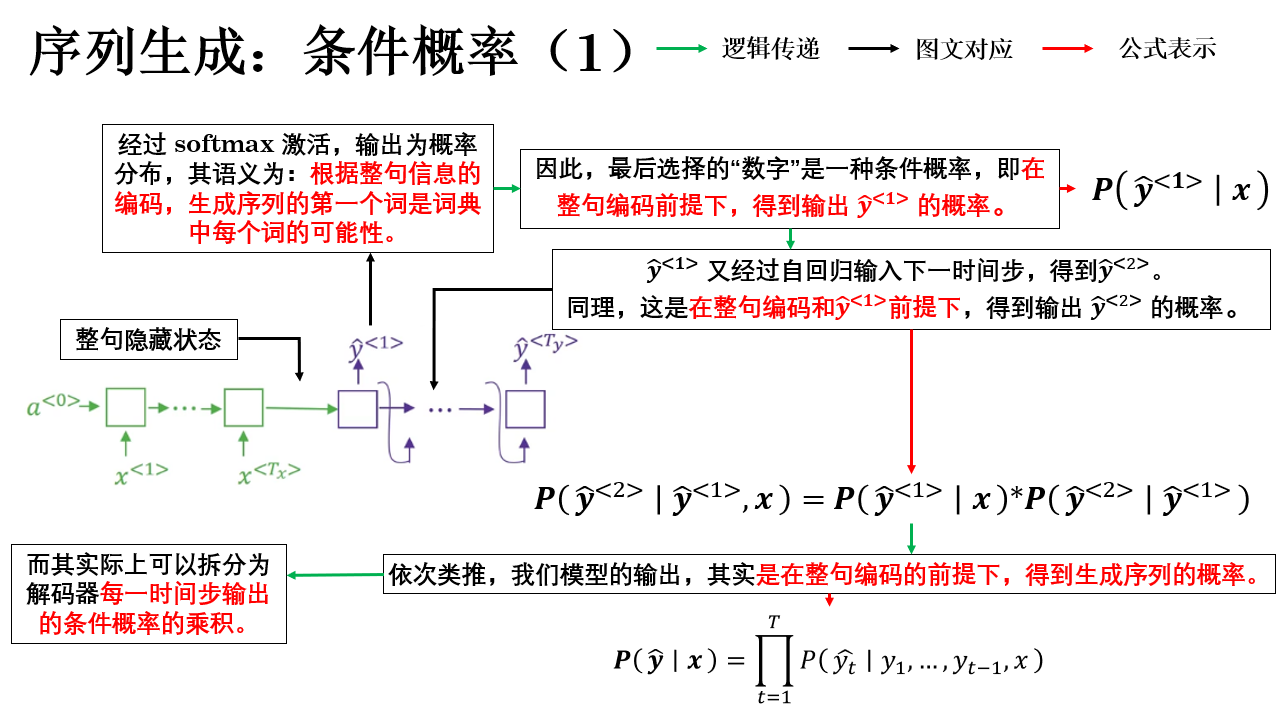
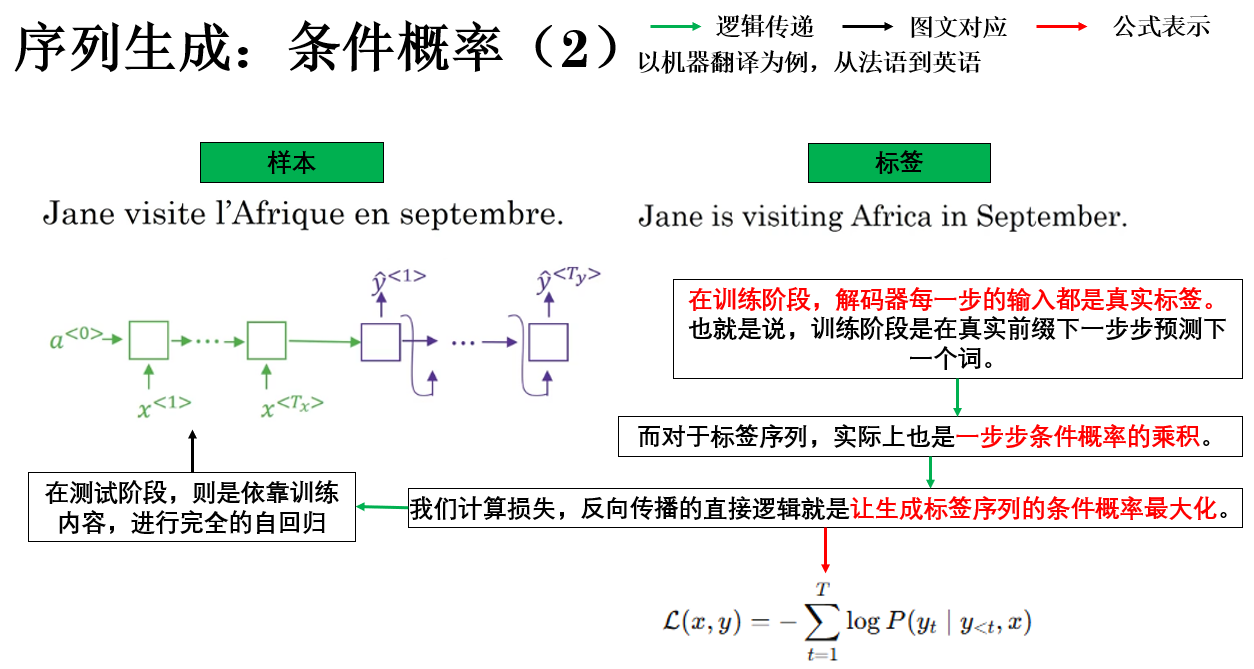
总结来说，seq2seq 模型真正面对的问题，是在所有可能的输出序列中，找到一个条件概率最大的序列。
通过概率链式法则，整句的条件概率可以被分解为若干个逐时间步的条件概率的乘积。
因此，我们在训练阶段学习得到更真实的概率分布，而在推理阶段，输出问题被转化为一个搜索问题：需要在由词表构成的序列空间中，寻找条件概率最大的那条生成路径。
就像这样：

但是，一个很明显的问题出现了，如果把所有可能的生成路径画成一棵树：深度为序列长度 \(T\)、每一层的分支数约为 \(|V|\)，那么完整搜索空间的规模大致为：\(|V|^T\)。
这是一个指数级增长的空间，显然不可能被穷举。

因此，你会发现，到这里，问题居然回归到了搜索算法中。

1.2 最直接的搜索策略：贪心算法

我们知道，既然每一步都会生成对应的概率分布，那么一个最直接的策略就是：在每一个时间步都选择条件概率最大的词作为当前输出，只保留这一条唯一的生成路径。
这种做法通常被称为贪心解码（Greedy Decoding）。

从形式上看，贪心算法在第 \(t\) 步执行的是：

\[\hat y_t = \arg\max_{w \in V} P(w \mid \hat y_{<t}, x) \]

并将该结果立即作为下一步的输入，直到生成终止符 EOS 或达到最大长度。

显然，贪心算法最大的优势在于极低的计算成本，它每一步只保留一个候选，不需要维护多条路径。因此解码速度快、内存占用小，对同一输入始终生成唯一输出，结果稳定。

但是，贪心算法的缺陷也是老生常谈了：局部最优不等于全局最优。
继续用刚刚的例子：

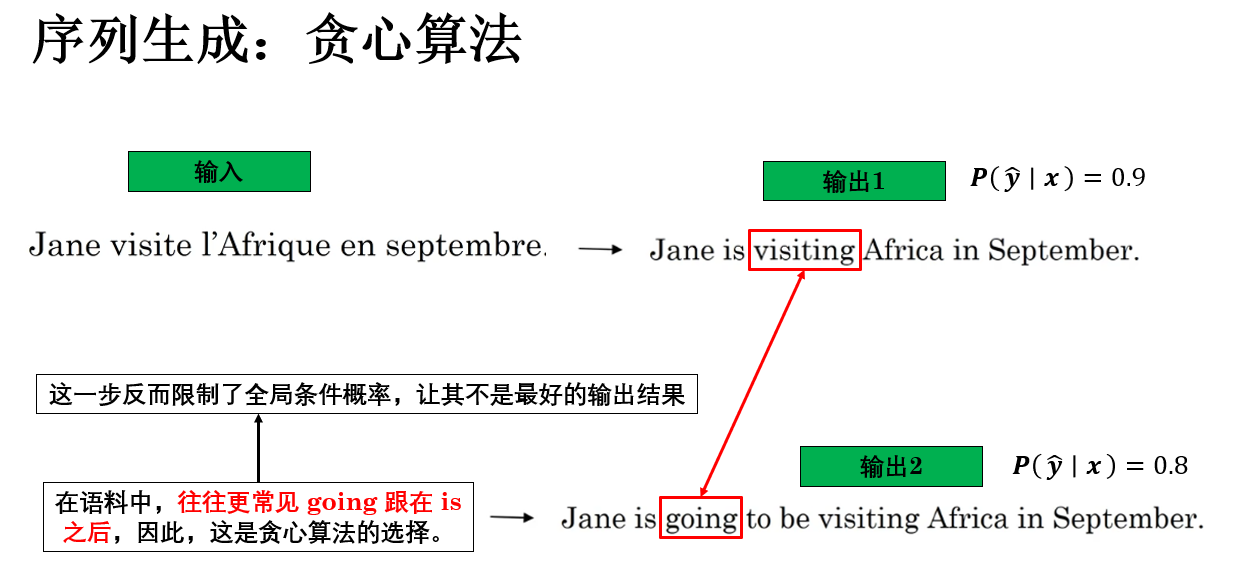
因此，由于贪心算法在每一步只关注当前条件下概率最大的词，而完全不考虑未来的影响，很容易出现某一步看起来是“最合理”的选择，但实际却会在后续步骤中限制模型的表达空间，最终导致整条序列的联合概率反而更低的情况。

总结来说，在对实时性要求较高、或对生成质量要求不高的场景中，贪心算法往往是一个工程上可接受的基线方案。但显然，它并不是一个很好的选择。

也正因为如此，我们才需要一种在计算代价可控的前提下，同时保留多条高概率候选路径的搜索策略—— 这正是束搜索（Beam Search）要解决的问题。

2. 束搜索（Beam Search）

在理解了序列生成和贪心解码后，束搜索的理解反而可以说是水到渠成，用一句话来概括束搜索：没有那么贪心的贪心算法。
贪心算法的问题在于，它只保留一条路径，导致容易错过整体概率更高的序列。
而束搜索的核心思想很简单：

在每一步生成时，不只保留一个最优词，而是保留前 \(k\) 条最有希望的候选序列，逐步扩展，最后从这些候选中选择联合概率最大的序列。

这里的 \(k\) 就是我们称为 束宽（beam width），它控制搜索的“宽度”：

• \(k=1\) 时，束搜索退化为贪心算法。
• \(k\) 越大，搜索空间越广，生成结果越接近全局最优。
• \(k\) 太大，又会带来计算开销增加。

不难理解，下面具体展开一下：

2.1 束搜索的步骤

假设词表大小为 \(|V|\)，beam width 为 \(k\)，束搜索的详细步骤如下：

1. 初始：从起始符 <BOS> 开始，生成第一步所有词的概率分布，选取前 \(k\) 个概率最高的词，组成初始候选序列。
2. 扩展：对每条候选序列，生成下一步的所有词的概率，计算每条扩展后序列的联合概率。
3. 保留：从 \(k \times |V|\) 条扩展序列中，选取联合概率前 \(k\) 的序列作为下一步候选。
4. 循环：重复步骤 2-3，直到每条候选序列生成 EOS 或达到最大长度。
5. 输出：从最终候选序列中选择联合概率最大的作为最终生成结果。

假设词表 \(V = {A, B, C}\)、目标序列最大长度 \(T = 3\)、束宽 \(k = 2\),我们举例来演示一下：

步骤 1：初始化

• 从起始符 <BOS> 出发，生成第一步所有词概率：$A=0.5, B=0.3, C=0.2
• 选前 \(k=2\) 个词：A (0.5) 和 B (0.3)

此时的候选序列池：\([A], [B]\)

步骤 2：扩展第一步候选

假定下一步生成概率分布如下：

候选序列	A	B	C
<BOS>+A	0.1	0.6	0.3
<BOS>+B	0.4	0.4	0.2

扩展过程为：

前一步序列	扩展词	新序列	计算过程	联合概率
[A]	A	[A,A]	0.5 × 0.1	0.05
[A]	B	[A,B]	0.5 × 0.6	0.30
[A]	C	[A,C]	0.5 × 0.3	0.15
[B]	A	[B,A]	0.3 × 0.4	0.12
[B]	B	[B,B]	0.3 × 0.4	0.12
[B]	C	[B,C]	0.3 × 0.2	0.06

此时的候选序列池：[A,B], [A,C]

步骤 3：扩展第二步候选

继续，假设模型在第 3 步生成概率如下：

序列	A	B	C
[A,B]	0.2	0.5	0.3
[A,C]	0.6	0.1	0.3

同理：

前一步序列	扩展词	新序列	计算过程	联合概率
[A,B]	A	[A,B,A]	0.3 × 0.2	0.06
[A,B]	B	[A,B,B]	0.3 × 0.5	0.15
[A,B]	C	[A,B,C]	0.3 × 0.3	0.09
[A,C]	A	[A,C,A]	0.15 × 0.6	0.09
[A,C]	B	[A,C,B]	0.15 × 0.1	0.015
[A,C]	C	[A,C,C]	0.15 × 0.3	0.045

需要强调的是：遇到相同概率的序列，本质上束搜索并没有硬性规定选哪条，可以根据场景选择：先到先得、随机或增加规则来提升多样性。
最终，我们完成扩展如下：

排名	序列	联合概率
1	[A,B,B]	0.15
2	[A,B,C]	0.09

因此最终输出序列为：[A,B,B]

这就是束搜索的直观机制：在可控开销下，同时考虑多条路径，提高生成序列的整体概率。

2.2 长度归一化（Length Normalization）

在上面的例子中，我们看到束搜索通过联合概率选择了 [A,B,B] 作为最终输出。
但是，在实际应用中，有一个容易被忽视的问题：联合概率是每一步条件概率的乘积，序列越长，乘积值往往越小。
也就是说，如果我们直接用联合概率来比较不同长度的序列，束搜索可能偏向生成短序列，因为它们乘起来的概率更大，而不是因为内容更合理。
因此，我们引入长度归一化，它和 BELU 里的长度惩罚有相同的出发点，但长度归一化是在“生成阶段做内部优化”，BLEU 长度惩罚是在“评价阶段修正指标”，两者原理类似，但作用环节不同。

具体来说，假设有两条候选序列：

序列	联合概率
[A,B,B]	0.15
[A,B,B,C]	0.14

其中，[A,B,B,C] 实际上可能更合理、语义更完整，但是因为联合概率 0.14 < 0.15，直接比较会被 [A,B,B] 优先选中，这就是“短序列偏好”问题。

而长度归一化的思路很简单：

用联合概率开根号或除以长度的函数，平衡序列长度的影响，使得长序列不会因为乘积小而被不公平地排除。

常见做法的就是加权归一化，对于长度 \(T\) :

\[\text{score}(\mathbf{y}) = \frac{1}{T^\alpha} \sum_{t=1}^{T} \log P(y_t \mid y_{<t}, x) \]

其中，\(\alpha \in [0,1]\) 是超参数，用来控制长度惩罚强度，而使用 log 用来防止下溢。

还是用刚刚的例子：

序列	联合概率	log 联合概率
[A,B,B]	0.15	\(\log 0.15 \approx -1.897\)
[A,B,B,C]	0.14	\(\log 0.14 \approx -1.966\)

假设 \(\alpha = 0.7\)，计算两条序列的归一化得分：

1. [A,B,B]，长度 \(T=3\)：

\[ \text{score}([A,B,B]) = \frac{-1.897}{3^{0.7}} \approx \frac{-1.897}{1.933} \approx -0.981 \]

2. [A,B,B,C]，长度 \(T=4\)：

\[ \text{score}([A,B,B,C]) = \frac{-1.966}{4^{0.7}} \approx \frac{-1.966}{2.639} \approx -0.745 \]

归一化后：

序列	原联合概率	归一化得分
[A,B,B]	0.15	-0.981
[A,B,B,C]	0.14	-0.745

现在，[A,B,B,C] 得分更高，此时束搜索就会选择更合理、更完整的长序列。
这样就解决了短序列偏好问题，同时保留概率信息。

2.3 束搜索的误差分析

到此为止，你会发现序列生成任务的性能被分成了两部分：模型对概率分布的拟合能力和搜索算法的搜索能力。
因此，在调试时的一个关键点就在于正确分析误差是来自模型还是搜索算法。
我们有这样一个方法来确认这一点：

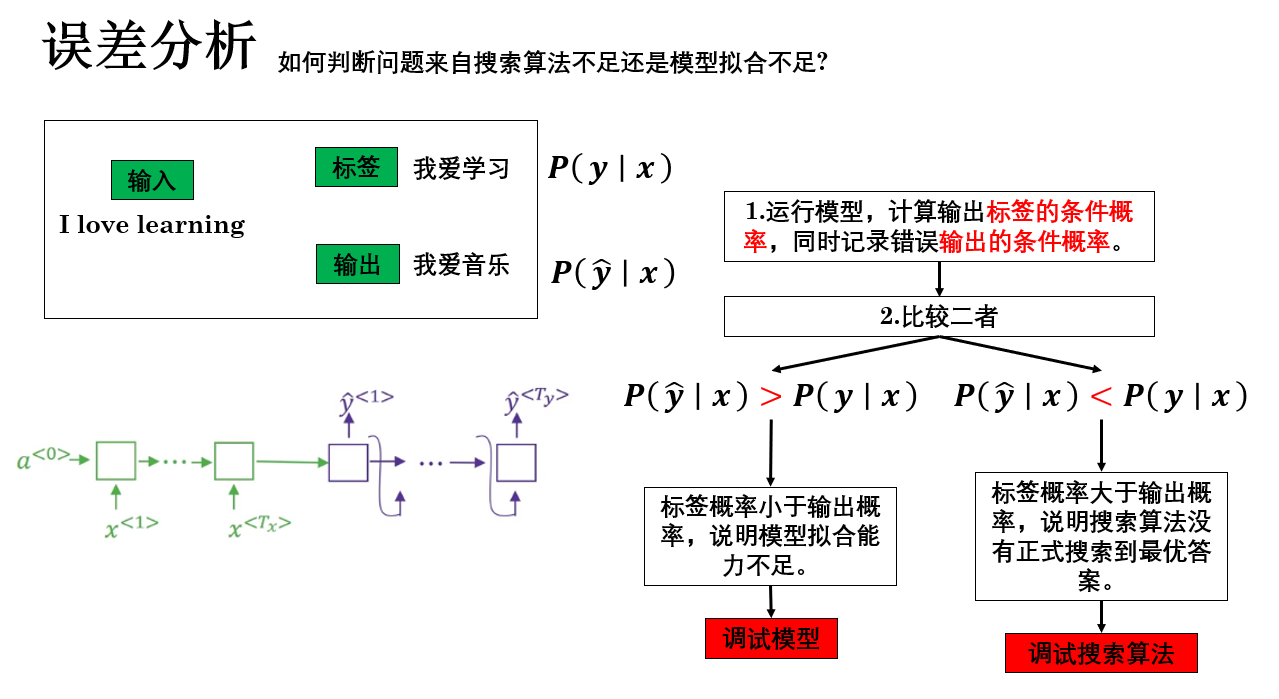
这样，通过标签序列的条件概率和输出序列的条件概率的大小关系，我们就可以确认误差来自模型还是搜索算法：

• 如果 \(P(\hat y|x) < P(y|x)\) → 搜索算法没找到最优序列 → 调试搜索算法。
• 如果 \(P(\hat y|x) > P(y|x)\) → 模型预测概率不准 → 调试模型。

3. 总结

概念	原理	比喻
序列生成的本质	seq2seq 模型在生成序列时，本质是求解条件概率最大的输出序列，即 \(\mathbf{y}^* = \arg\max_\mathbf{y} P(\mathbf{y} \mid x)\)，通过链式法则分解为逐步条件概率乘积。	找到所有可能路径中“最顺滑的一条”，像走迷宫选概率最高的路线。
贪心解码 (Greedy Decoding)	每一步选择条件概率最大的词作为输出，只保留一条生成路径，直到 EOS 或达到最大长度。	每次路口都选最宽的路，不管后面是不是死胡同。
束搜索 (Beam Search)	每一步保留前 \(k\) 条联合概率最高的候选序列，逐步扩展，最后从候选中选联合概率最大的序列。束宽 \(k\) 控制搜索空间大小。	没那么贪心的贪心算法，同时关注几条有潜力的路线。
短序列偏好问题	联合概率是条件概率乘积，序列越长乘积越小，束搜索可能偏向生成短序列。	短路优先：短的路线容易被选中，即便长的路线更合理。
长度归一化 (Length Normalization)	对联合概率取 log 后除以序列长度的函数或加权幂，平衡长度影响，使长序列不会被排除。公式：\(\text{score}(\mathbf{y}) = \frac{1}{T^\alpha} \sum_{t=1}^{T} \log P(y_t \mid y_{<t}, x)\)	给长路线加上“护栏”，让它有机会被选中。
束搜索误差分析	若 \(P(\hat y|x) < P(y|x)\) → 搜索没找到最优序列，问题在搜索算法。 若 \(P(\hat y|x) > P(y|x)\) → 模型给了高概率错误序列，问题在模型预测。	最好的水果就在货架上，但没找到 → 找东西的方法有问题 拿到的水果比最好的水果看起来更好，但实际上不好吃 → 判断水果质量的眼光不准