吴恩达深度学习课程五：自然语言处理 第二周：词嵌入（四）分层 softmax 和负采样

此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第五课的第二周内容，2.7的内容以及一些相关知识的补充。

---

本周为第五课的第二周内容，与 CV 相对应的，这一课所有内容的中心只有一个：自然语言处理（Natural Language Processing，NLP）。
应用在深度学习里，它是专门用来进行文本与序列信息建模的模型和技术，本质上是在全连接网络与统计语言模型基础上的一次“结构化特化”，也是人工智能中最贴近人类思维表达方式的重要研究方向之一。
这一整节课同样涉及大量需要反复消化的内容，横跨机器学习、概率统计、线性代数以及语言学直觉。
语言不像图像那样“直观可见”，更多是抽象符号与上下文关系的组合，因此理解门槛反而更高。
因此，我同样会尽量补足必要的背景知识，尽可能用比喻和实例降低理解难度。
本周的内容关于词嵌入，是一种相对于独热编码，更能保留语义信息的文本编码方式。通过词嵌入，模型不再只是“记住”词本身，而是能够基于语义关系进行泛化，在一定程度上实现类似“举一反三”的效果。词嵌入是 NLP 领域中最重要的基础技术之一。

本篇的内容关于分层 softmax 和负采样，是用来提升词嵌入模型训练效率，节省计算开销的技术。

1. 分层 softmax

在上一篇介绍 Word2Vec 的时候，我们默认使用的是标准 softmax 来计算输出层的概率分布。但如果稍微停下来仔细想一想，就会立刻意识到一个问题：在大词表场景下，标准 softmax 几乎是不可用的。

下面我们分点来展开标准 softmax 在词嵌入中的局限和分层 softmax 的思想：

1.1 标准 softmax 的计算开销

在之前的示例中，我们反复强调过一点：输出层的神经元个数与词典大小完全一致。
这是因为，在 Word2Vec 的建模视角下，预测过程本质上可以被看作一个单标签分类问题：

• 目标词对应“正确类别”
• 词表中其余所有词都对应“错误类别”

因此，我们需要通过 softmax 将模型输出映射为一个对整个词表的概率分布，并在反向传播阶段不断强化正确预测、抑制错误预测。

从建模逻辑上看，这一过程是完全合理的，但真正的问题，并不出在“对不对”，而是“能不能实现”。

我们知道，在 NLP 任务中，如果希望模型具备更强的泛化能力，第一步往往就是扩大语料规模，进而构建更大的词典。
而当我们希望模型在现实场景中“真正好用”时，其性能指标往往需要不断逼近，甚至尝试超越我们之前介绍过的贝叶斯最优错误率。
在这个意义上，词典规模并不是一个可有可无的工程参数，而是模型能力的硬上限。

一个直观的类比就是：人类的大脑究竟“记住”了多少词？ 显然，这绝不是一个可以用“几千”或“几万”来描述的数量级。

问题也正是在这里开始显现的：对于一次标准 softmax 计算而言，如果词表大小为 \(|V|\)，那么模型在输出层需要完成的操作包括：

1. 对 \(|V|\) 个词向量 分别计算内积。
2. 对 \(|V|\) 个得分 进行指数运算。
3. 对所有结果求和并完成归一化。

其计算形式可以写成：

\[P(w_o \mid w_c)= \frac{\exp(\mathbf{u}_{w_o}^\top \mathbf{v}_{w_c})} {\sum_{w \in V} \exp(\mathbf{u}_w^\top \mathbf{v}_{w_c})} \]

注意，这里省略了 softmax 输出层的偏置项，在 Word2Vec 的实际建模与实现中，该偏置对词向量语义结构的影响通常可以忽略，这是很简单的道理：我们需要刻画向量间的距离关系，而偏置带来的整体平移显然是没有意义的。

回到正题，也就是说，哪怕我们只关心一个目标词的概率， 模型仍然必须对整个词表中的所有词各计算一遍打分。

因此，每一个训练样本在输出层的计算复杂度都是：\(O(|V|)\)。
当 \(|V|\) 只有几千时，这个代价尚可接受，但一旦词典规模达到几十万、甚至上百万级别，这一步计算就会迅速成为训练过程中的主要瓶颈。
换句话说，标准 softmax 的计算成本与词表规模线性相关，这一性质在大词表场景下是无法回避的。
用我们之前的内容来类比一下：你见过几百万类别的分类模型吗？
也正是在这样的背景下，我们不得不思考新的问题： 可不可以在不显式遍历整个词表的前提下，完成对目标词的有效建模？

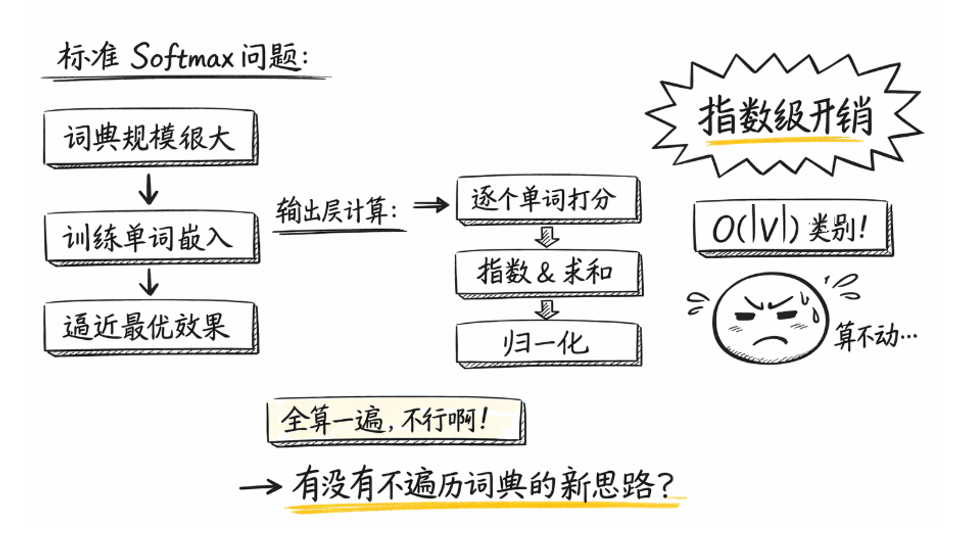
于是，Word2Vec 提出了第一种加速策略：分层 softmax。

1.2 哈夫曼树

哈夫曼是其实是数据结构里的内容，我们看看它在分层softmax中实现的效果。

哈夫曼树最早被用于无损数据压缩，其核心思想可以概括为一句话：出现频率越高的符号，编码越短；出现频率越低的符号，编码越长。 通过这种方式，高频符号拥有更短的路径长度，从而在整体意义下最小化编码的期望长度。

在 分层softmax 中，并没有使用其压缩编码的逻辑，而是重点利用哈夫曼树中高频符号拥有更短的路径长度的特点来组织词表并优化传播逻辑，它的过程如下：

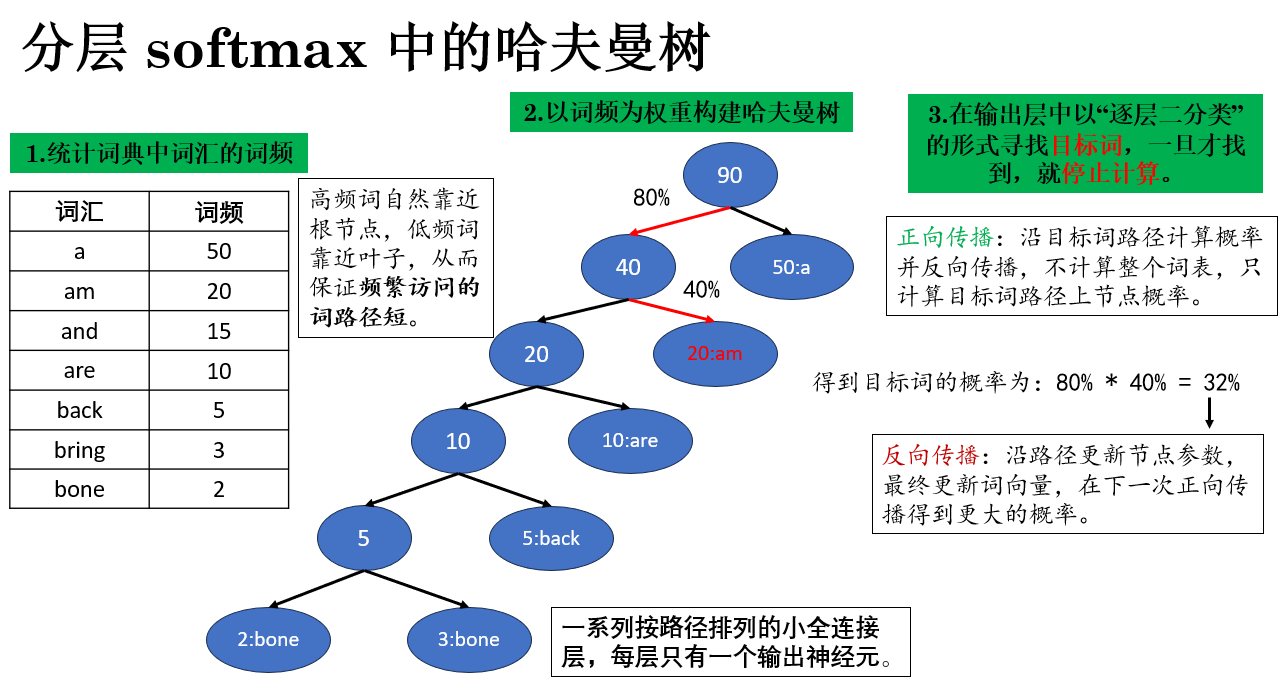
再具体来说，Word2Vec 的分层 softmax 将词表组织成哈夫曼树的步骤如下：

1. 统计词频：首先对语料库中的每个词计算出现频率，频率越高的词表示越常见，也就越可能在训练中被访问多次。
2. 构建哈夫曼树：
   • 将每个词作为叶子节点，节点权重 = 词频；
   • 从最小权重的两个节点开始合并，生成新的父节点，权重为子节点权重之和；
   • 重复此过程，直到只剩下根节点。
     通过这种方式，高频词自然靠近根节点，低频词靠近叶子，从而保证频繁访问的词路径短。
3. 路径作为概率计算序列：
   • 每条从根到叶子的路径对应一次概率计算的序列：每个节点上的选择可以看作一次二分类（是否沿左/右分支走）。
   • 目标词的概率 = 路径上所有二分类概率的乘积。
4. 降低训练开销：
   • 高频词路径短 → 更新梯度的节点少 → 每次训练样本计算量小。
   • 低频词路径长 → 虽然节点多，但训练中出现频率低，对整体训练开销影响小。
   • 整体而言，平均计算复杂度从 \(O(|V|)\) 降到 \(O(\log |V|)\)，极大提升了大词表场景下的训练效率。

只看到这里，可能还是有些模糊，我们以 CBOW 为例，来看看使用分层 softmax 的整体网络结构和传播过程。

1.3 CBOW 中的分层 softmax

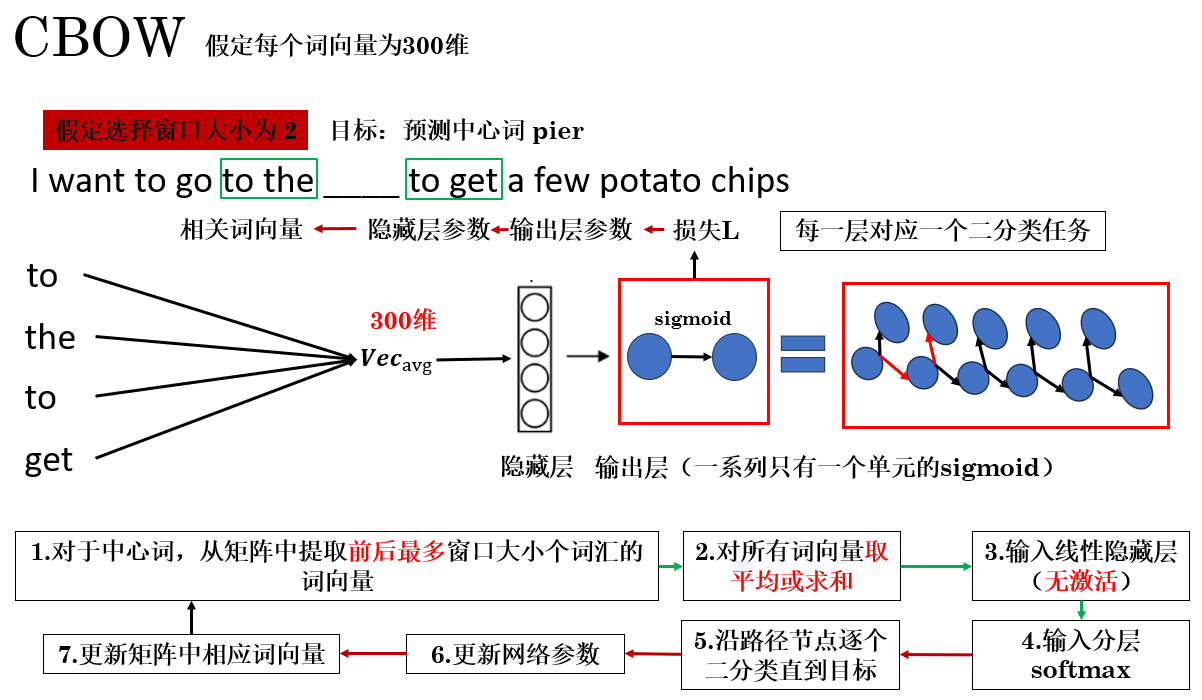
这样，最终效果是：一个原本包含几百万类别的输出问题，被分解成了一系列二分类问题。
在每次训练时，网络只需更新目标词路径上的相关节点参数，而不必触及整个输出层，从而大幅节省计算开销。
同时，由于哈夫曼树天然按照词频组织，高频词位于靠近根节点的路径上，使得这些词的更新路径更短、访问更快。这不仅加速了高频词的学习，也让整体训练过程更加高效。

这便是分层 softmax 的原理，如果从实际应用上来说，你也可以叫它”堆叠 sigmoid“，而 CBOW 便常常和分层 softmax 搭配使用。

下面我们便来看看另一种加速策略：负采样。

2. 负采样（Negative Sampling）

如果说分层 softmax 是一种结构层面的加速，那么负采样更像是一种从目标函数层面“改问题”的方法。
它的出发点非常直接：我们真的有必要在训练时区分“目标词”和“所有非目标词”吗？
答案是：不需要。
相较于分层 softmax，负采样的思想更加朴素、实现也更加简单。在实际工程中，它几乎可以看作是 Skip-gram 的默认搭档，也是 Word2Vec 最常被使用的训练方式之一。

负采样的核心思想可以概括为一句话：只挑选少量负样本进行训练，而非遍历整个词表。换句话说，我们只关心“正确词 + 一些随机挑选的错误词”，其他的全体词不参与计算。
这样，计算量从 \(O(|V|)\) 直接降到了 \(O(k)\)，其中 \(k\) 是负样本的数量（通常 \(5 \sim 20\)）。

我们以 Skip-gram 为例来演示负采样的原理：

2.1 确定正负样本

使用负采样的第一步是确定正负样本，这一过程同样容易理解，来看看：

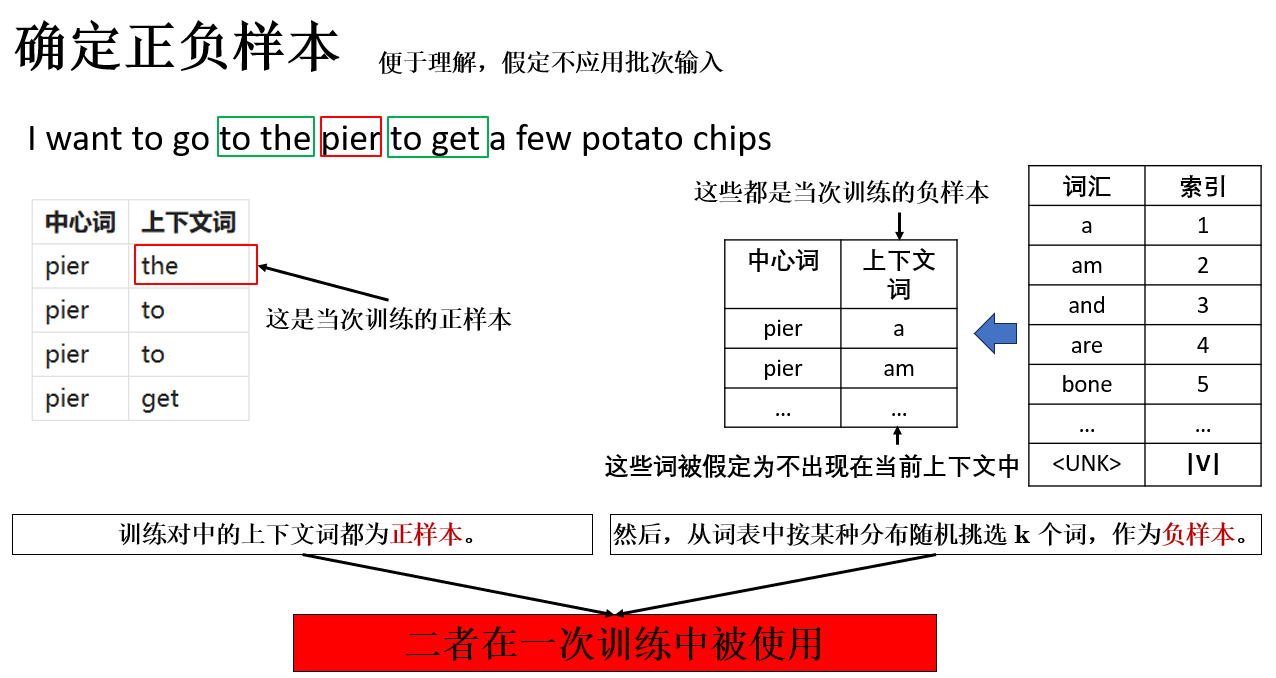
其中：

• 正样本：由真实语料中出现的上下文词构成；
• 负样本：从词表中随机抽取，但并不出现在当前上下文中的词。

这里展开一点，对于负样本的采样，我们常常使用下面这个公式：

\[P(w) \propto U(w)^{3/4} \]

• \(P(w)\)：表示在负采样中抽到词 \(w\) 的概率。
• \(U(w)\)：表示词 \(w\) 在整个语料库中的出现频率。
• \(\propto\)：表示“与……成正比”，意思是我们先按这个规则给每个词一个权重，再归一化成概率。

语言描述就是：先算每个词的词频的四分之三次方，然后把它们除以所有词的词频的四分之三次方 之和，就得到最终抽样概率 \(P(w)\)：

\[P(w) = \frac{U(w)^{3/4}}{\sum_{w' \in V} U(w')^{3/4}} \]

这个公式实际上做的是这样的工作：

1. 对高频词做了降权（比原始词频低一些），减少它们在负样本中出现的概率。
2. 对低频词做了相对提升（比直接按词频高一些），让它们有机会被采样到。

这种采样策略在实践中被证明可以提高词向量训练的稳定性和语义表达能力。
完成了数据准备后，现在，就来看看 Skip-gram 中的负采样。

2.2 Skip-gram 中的负采样

在 Skip-gram + 负采样 框架下，一次训练的传播过程可以概括为下图所示：

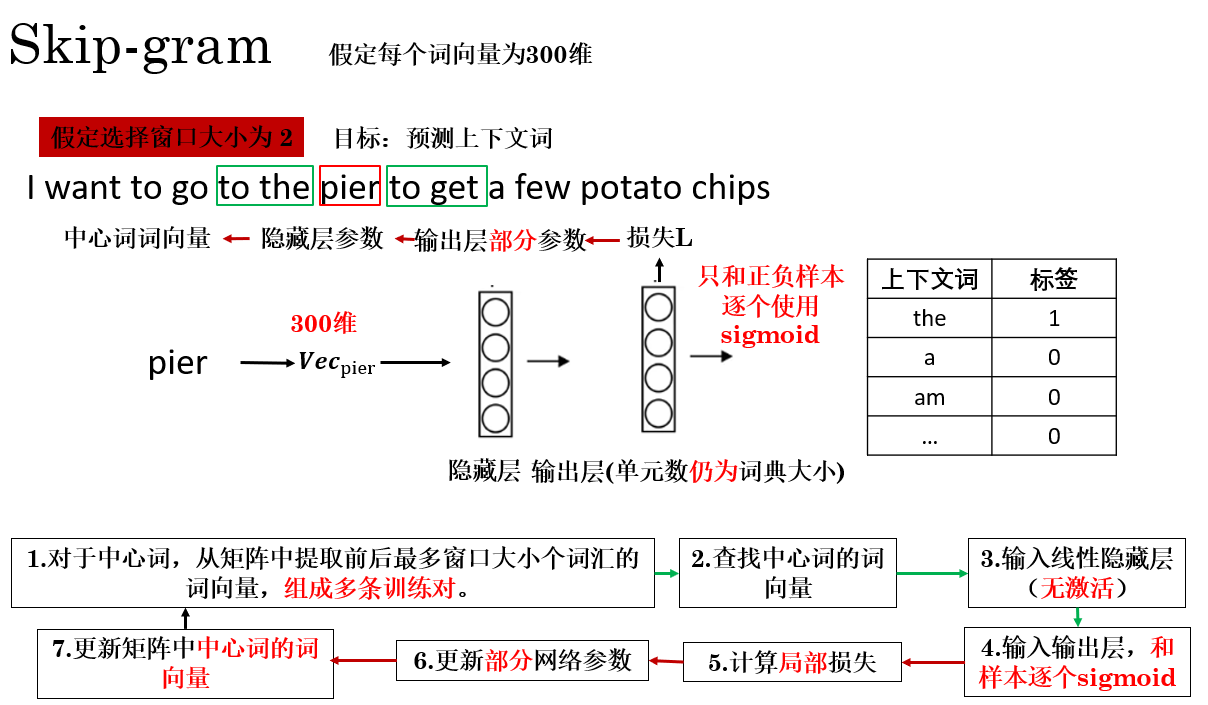
这种思路其实很容易理解：在一次传播中，我不再一次更新输出层的所有参数，而是只计算我提前挑选好的一些样本，只更新它们相关的参数，来节省计算开销，剩下的等下次选中再更新。

最终，模型仅更新正样本和 \(k\) 个负样本对应的输出层参数以及输入词向量，其余词的向量完全不参与更新，从而节省了大量计算，实现 \(O(k)\) 的复杂度，远小于 \(O(|V|)\)。
这种“只更新被选中参数”的训练方式，使得负采样在大规模语料与超大词表场景下，具备极高的计算效率。

你会发现，负采样和分层 softmax 的一点共同逻辑就是把一次多分类拆成了多次二分类，这同样是我们可以学习的优化思路。

3.总结

概念	原理	比喻
softmax大词表瓶颈	softmax 的计算与反向传播都必须遍历整个词表，词表越大，训练越慢，成为主要性能瓶颈	在问路时，必须问完全国所有居民
分层 softmax	用哈夫曼树将多分类问题拆成一条从根到叶的二分类决策路径，目标词概率等于路径上各二分类概率的乘积	在每个路口选择方向，而不是一次问遍所有人。
分层 softmax +CBOW	每次训练只更新目标词路径上的节点参数，其余词完全不参与计算	只维修你真正经过的路口，而不是重修整座城市。
负采样（Negative Sampling）	不再逼模型区分“目标词 vs 全词表”，而是区分“目标词 vs 少量噪声词”，复杂度为 \(O(k)\)	不用认清所有陌生人，只要确认朋友和几名路人
正负样本构造	正样本来自真实上下文；负样本从词表随机抽取但不在上下文中	真朋友 vs 随机拉来的假熟人
\(U(w)^{3/4}\) 采样分布	对高频词降权、对低频词相对提升，使负样本更有信息量	热门明星少出现点，路人多给点镜头
Skip-gram + 负采样	每次仅更新中心词、正样本词和 \(k\) 个负样本的向量，其余参数不动	只训练被点名的几个人，其他人下次再说