吴恩达深度学习课程五：自然语言处理 第一周：循环神经网络 （二）循环神经网络

此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第五课的第一周内容，1.2到1.4的内容。

---

本周为第五课的第一周内容，与 CV 相对应的，这一课所有内容的中心只有一个：自然语言处理（Natural Language Processing，NLP）。
应用在深度学习里，它是专门用来进行文本与序列信息建模的模型和技术，本质上是在全连接网络与统计语言模型基础上的一次“结构化特化”，也是人工智能中最贴近人类思维表达方式的重要研究方向之一。
这一整节课同样涉及大量需要反复消化的内容，横跨机器学习、概率统计、线性代数以及语言学直觉。
语言不像图像那样“直观可见”，更多是抽象符号与上下文关系的组合，因此理解门槛反而更高。
因此，我同样会尽量补足必要的背景知识，尽可能用比喻和实例降低理解难度。
本篇的内容关于循环神经网络，在 NLP 中，循环神经网络就像卷积网络在 CV 中一样，是处理序列数据的核心特化模型，专门用于捕捉上下文依赖。

1. NLP 中的符号规范

在正式开始引入循环神经网络前，我们同样需要先了解一些相关的符号规范，主要是在数据的表示方面。

1.1 模型的输入与输出

再复述一下：

1. \(x^{<t>}\) ：输入序列在第 \(t\) 个时间步的输入。
2. \(y^{<t>}\) ：输出序列在第 \(t\) 个时间步的输出。
3. \(T_x\)：输入序列的长度。
4. \(T_y\)：输出序列的长度。

现在，结合我们之前的符号规范，就可以知道：
\(X^{(n)<t>}\) 代表一批次输入中第 \(n\) 个样本的第 \(t\) 个元素。

1.2 词典（Vocabulary）

经过上一部分，我们知道，\(x^{<t>}\) 代表了一个序列中的某一个元素。
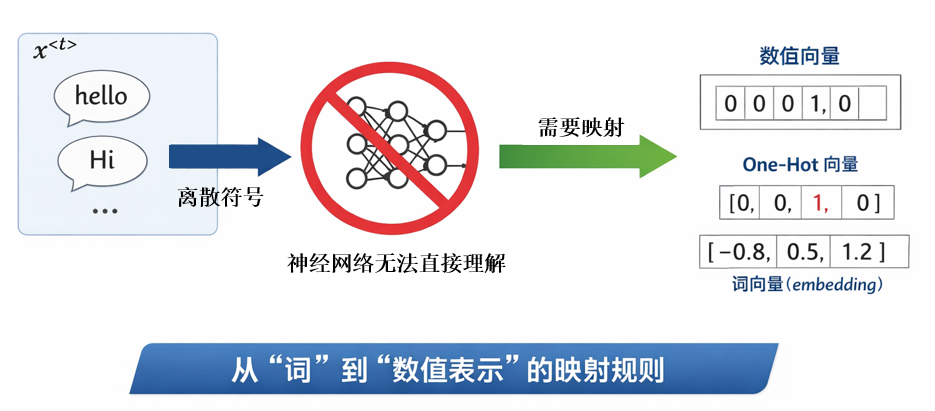
但是又有一个新的问题：在 NLP 任务中，\(x^{<t>}\) 往往是一个离散的符号，例如某个具体的词（如 hello、Hi），而神经网络本质上只能处理数值向量，并不能直接理解“词”这一抽象概念。

因此，在将文本序列送入模型之前，我们必须先完成一件事情：给“词”一个能输入网络的表示方法，即建立一种从“词”到“数值表示”的映射规则。
显然，这种映射关系必须是确定且唯一的，即每一个词都对应一个唯一的数值表示。
而其中一种表示方法，就是我们在多分类标签表示中使用的独热编码。
我们看一个简单的示例：
假设我们当前的词典只包含 4 个词：

\[{\text{hello},\ \text{Hi},\ \text{thanks},\ \text{bye}} \]

我们可以为词典中的每一个词分配一个唯一的索引：

\[\text{hello}\rightarrow 1,\quad \text{Hi}\rightarrow 2,\quad \text{thanks}\rightarrow 3,\quad \text{bye}\rightarrow 4 \]

在这种设定下，每一个词都可以用一个长度为 4 的独热向量来表示。
例如：

• \(\text{hello}\) 对应的表示为：\(x = [1,0,0,0]\)
• \(\text{Hi}\) 对应的表示为：\(x = [0,1,0,0]\)
  词典中的每个词都有且仅有一个位置为 1，其余位置全部为 0。
  从模型的角度来看，这样的表示方式意味着：模型在任意时刻接收到的输入，本质上是一个高维稀疏向量，这正好满足“词 → 数值向量”的一对一映射要求，因此能够直接作为神经网络的输入。

然而，在真实的 NLP 任务中，一个不可忽视的现实问题是：词典的规模通常非常巨大。
在常见的语言建模或翻译任务中，词典大小往往达到数万甚至百万级别。
这意味着：

• 独热向量的维度极高
• 向量极度稀疏
• 计算和存储成本都非常不经济

因此，在实际模型中，我们往往会采用一种更紧凑、也更具语义表达能力的词表示方法，叫做词向量（Embedding） ，我们会在之后的内容详细展开它。

此外，还会出现另一个问题： 测试或实际使用时，可能会遇到词典中从未出现过的词。
对于这种不在词典中的词（Out-Of-Vocabulary，OOV），常见的一种处理方式是在词典中额外引入一个特殊标记<UNK>，用于统一表示所有未知词，这种方式虽然简单，但也会丢失不同未知词之间的差异性，这也是后续子词建模方法要解决的问题之一。

这些我们都会在之后的实际演示中详细展开，现在，先了解简单的符号规范后，我们正式开始引入循环神经网络。

2. 循环神经网络（Recurrent Neural Network，RNN）

在上一篇对序列模型的介绍中，我们已经知道：全连接网络和卷积网络并不适合用来处理序列数据。
我们需要一种模型，在处理当前输入的同时，能够保留并更新对“过去信息”的表示，让模型在理解当前内容时，不是孤立地“看这一刻”，而是基于整个上下文来判断。
而这，就是 RNN 的基本思想。
RNN最早可追溯到 Jordan（1986）对序列连接主义模型的研究，而现代深度学习中常用的 RNN 基本形式，则来源于 Elman 在1990年发表的一篇论文： Finding Structure in Time中提出的递归状态网络结构。
可以看到，尽管论文距今已有几十年，但像最初的 CNN 一样，RNN 的思想并没有被时间淹没，而是不断被推广和创新，最终成为现代 NLP 中不可或缺的基础模型。

现在，我们用一个最简单的单层循环神经网络来介绍 RNN 的传播过程及其特点。

2.1 单层循环神经网络的结构

来看课程里这样一个循环网络的传播示意图：

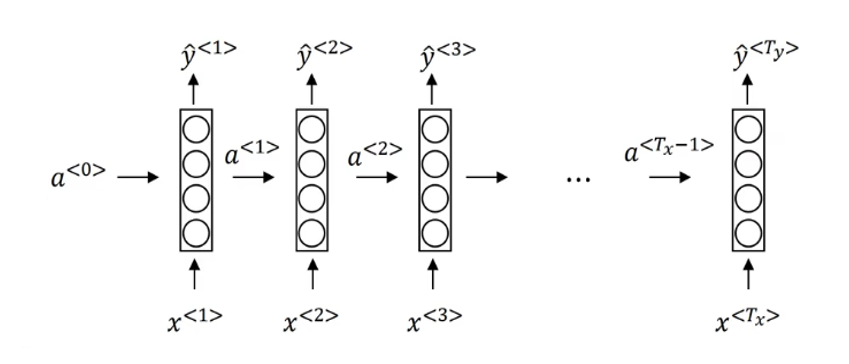
你可能会觉得，这个结构看起来好像不像传统意义上的“单层网络”，反而更像每一层都直接接收原始输入的全连接网络。
其实这正体现了 RNN 与 FN 或 CNN 的本质区别：在 RNN 中，每个时间步的隐藏状态不会直接传给下一层，而是传递给下一个时间步的自身。
也就是说，这个网络的实际结构是这样的：

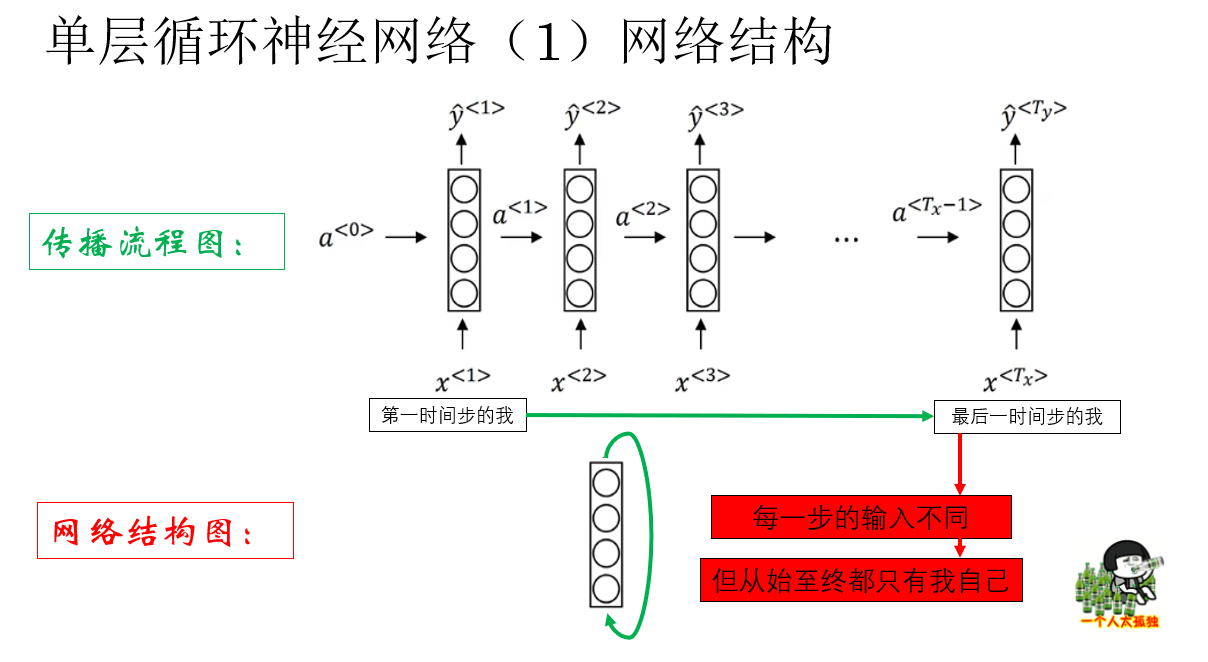
也就是说，RNN 本质上就是在全连接层基础上加了时间维度的循环连接。
你会发现，如果抛开传播逻辑不看，单层循环网络实际上就是一层全连接层。
但这也恰恰说明了它的传播逻辑的重要性，到底是怎么样的设计能让单层的全连接层一跃而成为 NLP 的基石？
我们继续。

2.2 单层循环神经网络的正向传播

了解了 RNN 的基本逻辑后， 现在，我们就来演示一下单层 RNN 的具体传播过程中的一些细节：

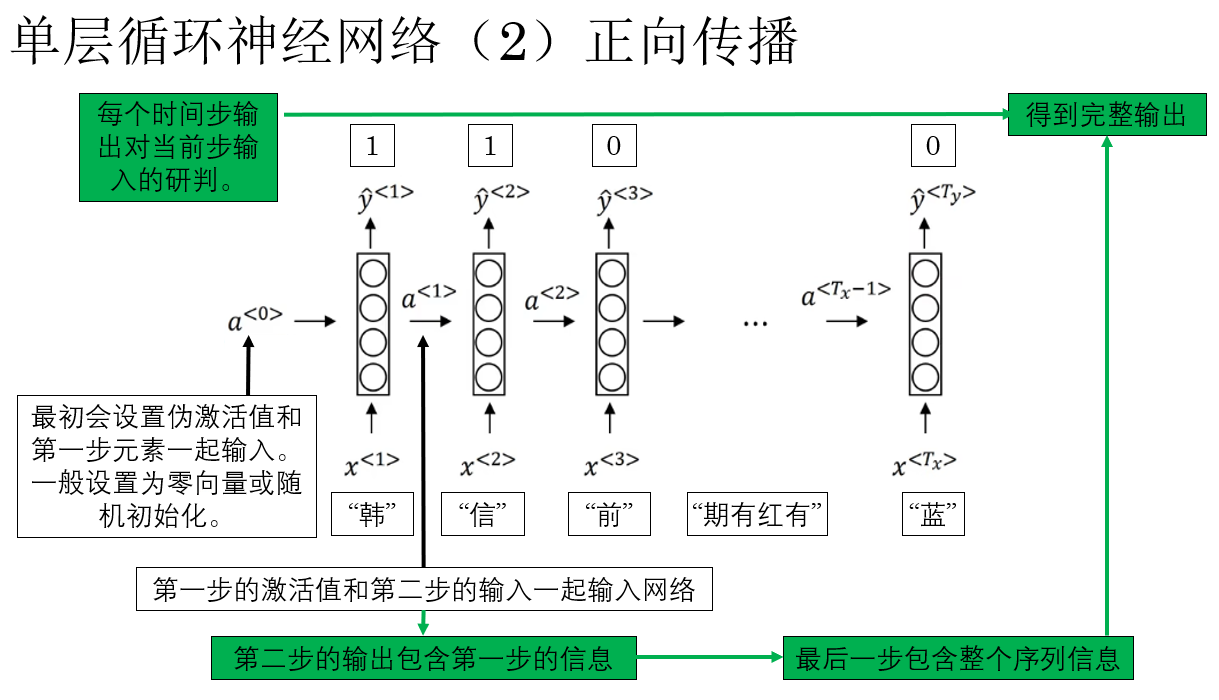
了解了这些后，我们规范一下单层 RNN 的正向传播过程：

1. 初始状态
   RNN 在第一个时间步输入第一个元素 \(x^{<1>}\)（例如“韩”）时，同时会引入初始的伪激活值 (\(a^{<0>}\)) 作为网络的初始状态，\(a^{<0>}\) 通常设为零向量或随机初始化。
2. 逐步处理序列
   每个时间步，RNN 会将当前输入 \(x^{<t>}\) 与上一时间步的隐藏状态 \(a^{<t-1>}\) 一起输入网络，计算当前的隐藏状态 \(a^{<t>}\),例如在第二步，输入为 \(x^{<2>}\)（“信”）和 \(a^{<1>}\)，得到 \(a^{<2>}\)。
3. 输出生成
   每一步的隐藏状态 \(a^{<t>}\) 都会产生一个预测输出 \(\hat{y}^{<t>}\)。输出不仅依赖当前输入，也包含了前面时间步的历史信息，这就是 RNN 能够“记忆”序列上下文的原因。
4. 信息传递
   隐藏状态会沿时间步向后传递，使后续时间步的输出能够利用之前所有的序列信息，最终一步输出 \(\hat{y}^{<T_x>}\) 包含整个序列的信息，可用于完整序列的预测或判断。

明白了传播逻辑后，我们便可以更好地理解 RNN 正向传播的公式表达，我们先说明一下网络中的参数表示：

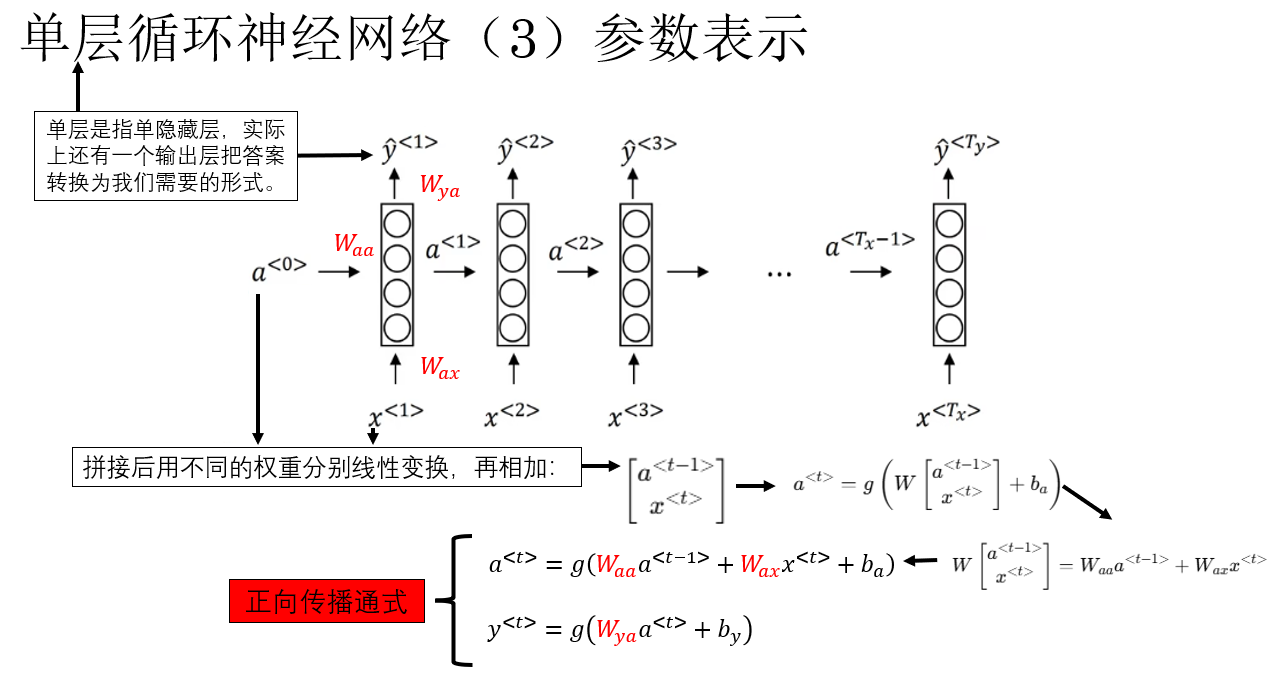
现在便摆出正向传播的通式如下：

\[a^{<t>} = g(W_{aa} a^{<t-1>} + W_{ax} x^{<t>} + b_a) \]

\[y^{<t>} = g(W_{ya} a^{<t>} + b_y) \]

总结一下：RNN 的正向传播就是每个时间步将当前输入和上一隐藏状态结合，更新当前隐藏状态并生成输出，隐藏状态沿时间步传递，从而使网络能够逐步累积和利用序列历史信息。

了解了正向传播的大致流程后，我们再看看 RNN 的反向传播是如何进行的。

2.3 单层循环神经网络的反向传播

经过上一部分，我们已经知道：RNN 的正向传播，本质上是在时间维度上反复使用同一组参数，并通过隐藏状态把历史信息向后传递。

那么问题自然就来了： 这些跨时间步传递的信息，反向传播时该怎么“算梯度”？

答案是： 怎么过去就怎么回来——RNN 的反向传播，并不是在“层”之间传播，而是在时间维度上反向传播，这种传播被称为 BPTT（Backpropagation Through Time） 。
我们来简要演示一下这个过程：

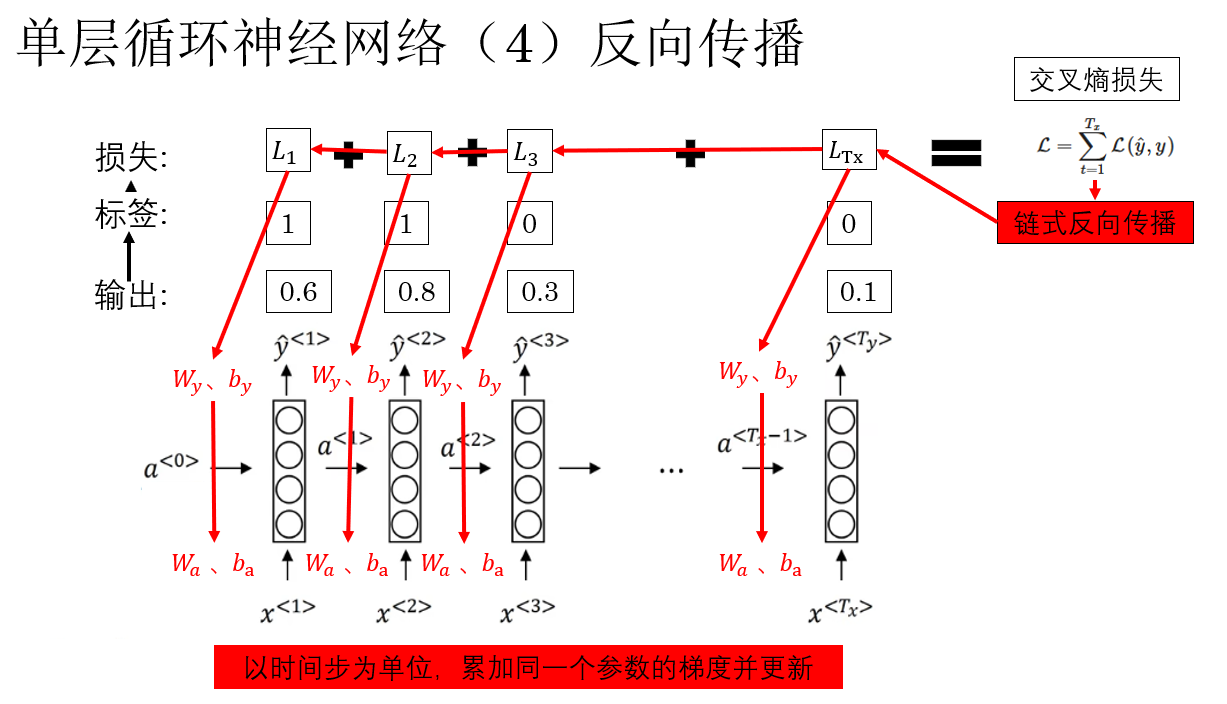
在监督学习中，反向传播的起点永远是损失函数，对于 RNN 来说，损失通常是所有时间步损失的累加（默认 \(T_x = T_y\)）：

\[\mathcal{L} = \sum_{t=1}^{T_x} \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>}) \]

也就是说，每一个时间步的输出都会对总损失产生贡献。
而对于单步的损失，最常用的仍然是我们比较熟悉的交叉熵损失,你可以通过链接查看我们之前的介绍，应用在 RNN 中，它的公式是这样的：

\[\mathcal{L} = \sum_{t=1}^{T_x} \left( - \sum_{k=1}^{C} y_k^{<t>} \log \hat{y}_k^{<t>} \right) \]

因此，反向传播时，我们会从最后一个时间步开始，逐步向前，把每个时间步的误差信号往回传， 由于参数在所有时间步共享，每个时间步的损失都会通过时间链路对这些参数产生梯度贡献，最终用于更新的梯度，是沿时间维度反向传播后，各时间步贡献的综合结果。

这就是单层循环神经网络的反向传播，这样我们就对 RNN 的基本运行逻辑有了大体的了解。

3.总结

概念	原理	比喻
序列数据	数据元素具有明确顺序，当前理解依赖历史上下文	一句话的意思要从前往后读，不能只看中间一个词。
时间步 \(t\)	序列中第 \(t\) 个位置，用于展开时间维度	时间轴上的第 \(t\) 帧画面。
输入 \(x^{}\)	第 \(t\) 个时间步送入模型的输入向量	当前这一秒你听到的一个词。
预测输出 \(\hat{y}^{}\)	模型在第 \(t\) 个时间步给出的预测结果	听到一句话后，此刻你做出的判断。
序列长度 \(T_x, T_y\)	输入序列与输出序列的长度（可相同或不同）	一段话的字数 vs 你回答时说了几句话。
词典（Vocabulary）	从词到索引的一一映射表	电话簿：名字 ↔ 电话号码
RNN 核心思想	当前状态由当前输入 + 过去状态共同决定	你理解一句话时，会不断修正之前的理解。
BPTT	梯度沿时间维度反向传播	从句尾倒回去反思：是哪一步理解错了。
梯度累积	参数梯度来自所有时间步的综合贡献	每一句话的错误都会影响你下次的理解方式。

。