吴恩达深度学习课程二: 改善深层神经网络 第二周:优化算法(六)课后习题和代码实践
此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第二课第二周的课程习题和代码实践部分笔记。
1.理论习题
【中英】【吴恩达课后测验】Course 2 - 改善深层神经网络 - 第二周测验
还是先上这位博主链接,然后这里我们挑出几道来展开一下。
1.1 符号规范
来看这道题:
当输入从第八个mini-batch的第七个的例子的时候,你会用哪种符号表示第三层的激活?
答案:\(a^{[3]\{8\}(7)}\)
随着几周的不断学习,也出现了越来越多的符号,我们在这里梳理一下:
| 符号 | 名称 | 含义 / 表示对象 | 备注说明 |
|---|---|---|---|
| \(x^{(i)}\) | 第 \(i\) 个样本输入 | 单个样本的输入特征列向量 | \(n_x\):输入层神经元个数 |
| \(y^{(i)}\) | 第 \(i\) 个样本标签 | 单个样本的输出(标量或向量) | 监督学习中的真实值 |
| \(X\) | 所有样本输入矩阵 | 把所有 \(x^{(i)}\) 横向拼接 | \(m\):样本总数 |
| \(Y\) | 所有样本标签矩阵 | 把所有 \(y^{(i)}\) 横向拼接 | 通常 \(n_y=1\) |
| \(X^{\{t\}}\) | 第 t 个 mini-batch 的输入矩阵 | 把该批次内的 \(x^{(i)}\) 横向拼接 | - |
| \(W^{[l]}\) | 第 \(l\) 层的权重矩阵 | 当前层与上一层之间的连接权重 | 由网络结构决定 |
| \(b^{[l]}\) | 第 \(l\) 层的偏置向量 | 当前层的偏置项 | 广播到所有样本 |
| \(z^{[l]}\) | 第 \(l\) 层的线性部分 | \(z^{[l]} = W^{[l]} a^{[l-1]} + b^{[l]}\) | 激活函数的输入 |
| \(a^{[l]}\) | 第 \(l\) 层的激活值 | \(a^{[l]} = g^{[l]}(z^{[l]})\) | 上层的输入 |
| \(g^{[l]}\) | 第 \(l\) 层激活函数 | 如 ReLU、Sigmoid、Tanh 等 | 与任务有关 |
| \(\hat{y}^{(i)}\) | 第 \(i\) 个样本的预测 | 模型的输出结果 | 预测值 |
| \(\hat{Y}\) | 所有样本的预测矩阵 | 所有 \(\hat{y}^{(i)}\) 拼接 | - |
| \(J\) | 成本函数 | 衡量预测与真实标签的差距 | 通常为交叉熵或均方误差 |
| \(\alpha\) | 学习率 | 控制参数更新步长 | 越大越快但不稳定 |
| \(v^{[l]}\) | 动量项 | EMA 平滑后的梯度方向 | Momentum / Adam 使用 |
| \(s^{[l]}\) 或 \(S^{[l]}\) | 平方梯度累积项 | EMA 平滑后的梯度平方 | RMSprop / Adam 使用 |
| \(t\) | 当前迭代次数(步数) | 优化算法中的时间步 | Adam 等算法中使用 |
| \(m\) | 样本总数 | - | 整个训练集大小 |
| \(m_{mini}\) | mini-batch 样本数 | - | 小批量训练用 |
| \(a^{[l]\{t\}(i)}\) | 特定样本与批次的激活 | 第 \(t\) 个 mini-batch,第 \(i\) 个样本,第 \(l\) 层激活 | 完整标记形式,精确到样本与批次 |
看起来有些繁杂,但实际上在这么长时间的使用里,我们已经记忆了大部分了。看一遍下来查漏补缺就好了。
唯一要强调的一个是\(X^{\{t\}}\) 中 \(\{t\}\) 代表的是Mini-batch 梯度下降中的第 \(t\) 个批次,\(X^{\{t\}}\) 是第 \(t\) 个批次的输入。
这是本周里随着Mini-batch 梯度下降出现而引入的新规范,但是在理论部分并没有实际用到,就放在了这里。
1.2 EMA 平滑系数辨析
看看题面:
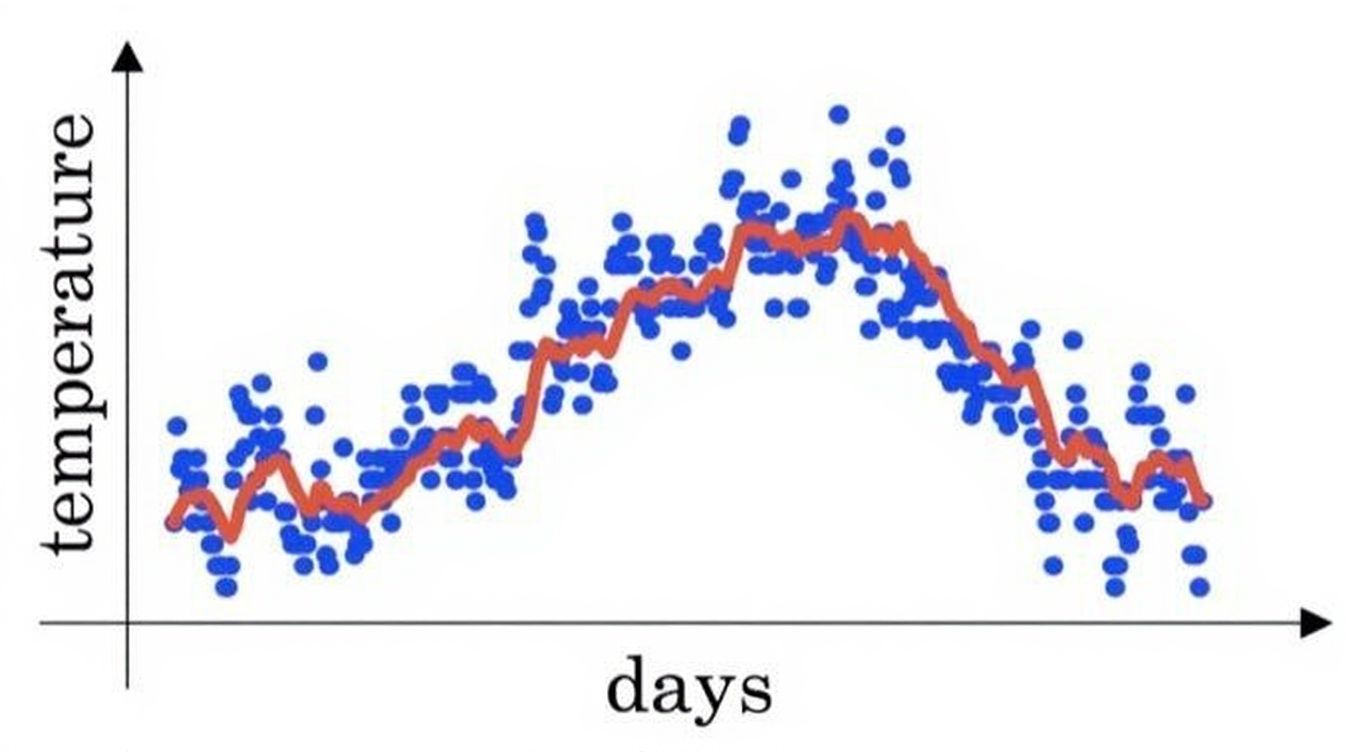
您在伦敦温度数据集上使用指数加权平均值, 您可以使用以下公式来追踪温度:\(v_t = βv_{t-1} +(1 - β)θ_t\) 下面的红线使用的是 \(β= 0.9\) 来计算的。 当你改变 \(β\) 时,你的红色曲线会怎样变化?
答案: 增加 \(β\) 会使红线稍微向右移动;减少 \(β\) 会在红线内产生更多的振荡。
回忆一下我们在指数加权平均部分对平滑系数的概念:它代表我们对“历史印象”的依赖程度。
- 平滑系数越大,平均值越注重“以前”的数据。
- 平滑系数越小,平均值越看重“今天”的数据。
实际上,EMA不同于简单平均的点就在于它能抹平短期波动的同时反应长期变化的方向。它反应的更像是一种“一段时间里的趋势”。
现在再来分析一下两个正确答案:
- 增加 \(β\) 会使红线稍微向右移动: 我们分析一下“右移”是什么意思,是不是当红线右移时,每一个点都会右移?也就是:今天的均值变成了明天的均值(时间滞后,并非真的平移)。
换句话说: 平滑后的曲线(红线)对真实数据(蓝线)的反应变得更滞后了。
再展开点:当 \(\beta\) 变大时,我们更依赖过去的历史值,那是不是对“今天”变化的敏感度就会降低?因此,红线的趋势变化更平缓,更“跟不上”蓝线(当天),看起来就像整体向右延迟了一点。 - 减少 \(β\) 会在红线内产生更多的振荡:其实是一个道理,我们再换一种说法来理解。
我们之前提到等效天数的概念,减少 \(β\) 会减少等效天数,相当于用更短的窗口捕捉趋势。那对“今天”变化的敏感度是不是就会增加?自然会更加“震荡”,因为反应的“趋势”更短期了,自然会趋势里的每一天更敏感。
如果还不太明白,我们再来看一道同类型的题:
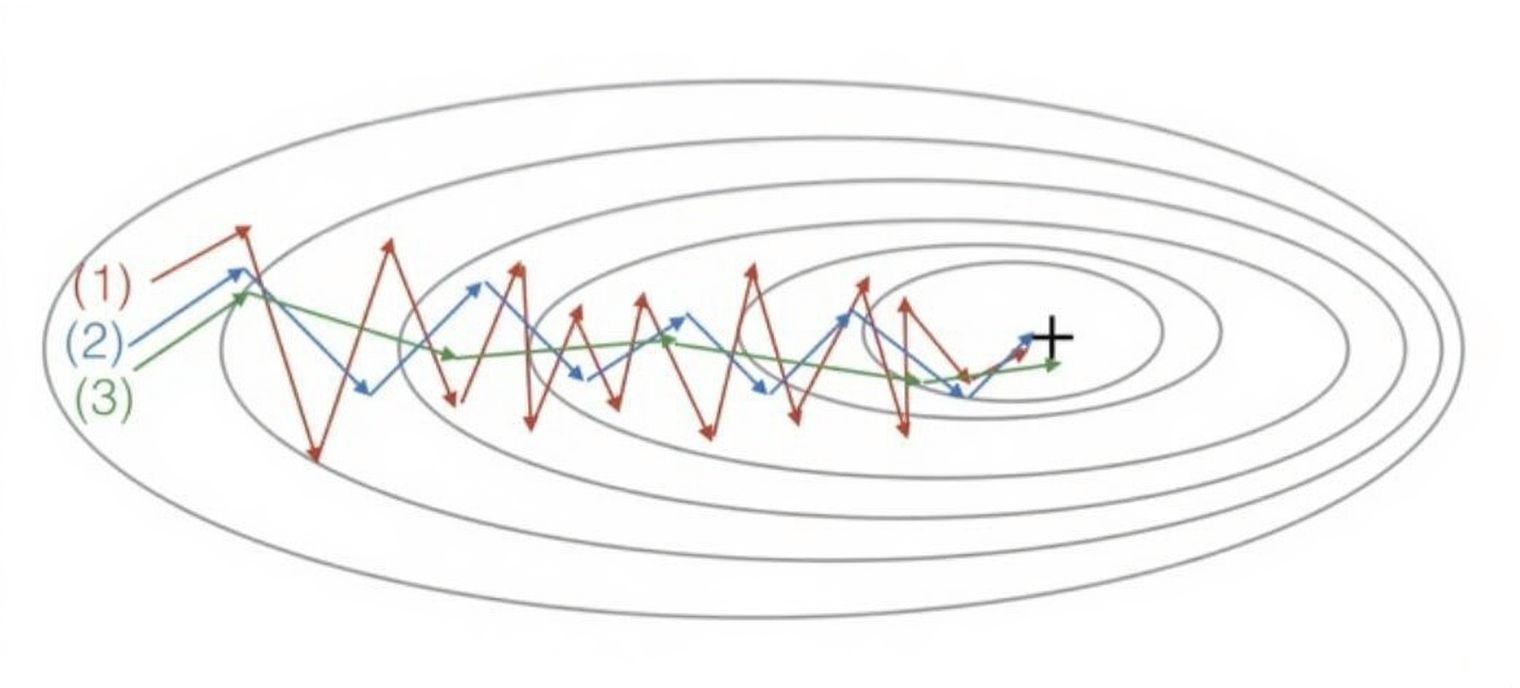
已知图像是由梯度下降产生的。那哪条曲线对应哪种下面算法?
A.普通的下降 B.具有动量梯度下降(β= 0.5) C.动量梯度下降(β= 0.9)
答案:(1)是梯度下降。 (2)是动量梯度下降(β值比较小)。 (3)是动量梯度下降(β比较大)
结合上面那到实际题,我们再来看看这到理论的题。
我们已知,Momntum 通过对梯度应用EMA来缓解振荡现象。
说简单点:就是对梯度取加权平均值应用更新,不过度依赖本次传播的计算的梯度。
这里的 ”当次传播“”是不是就相当于“当天气温”?
而 \(β\) 增加就相当于对以前越看重,那是不是反应的“趋势”就越长期?自然,多次上下抵消后纵向的波动就更小?
答案很容易就可以得到,重点是理解EMA的作用原理。
2.代码实践
【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络
还是先摆链接,对于本周的内容,这位博主依然只使用numpy库来手动构建各种优化算法。
我们也还是用我们的Pytorch框架把新的优化应用在猫狗二分类数据集来看看这几种优化算法的实际效果。
2.1 小批次,批量和随机梯度下降法
还是先回忆一下我们之前更新完的模型:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
# 输出层
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
# Xavier初始化输出层
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.relu(self.hidden3(x))
x = self.relu(self.hidden4(x))
x = self.relu(self.hidden5(x))
x = self.relu(self.hidden6(x))
x = self.sigmoid(self.output(x))
return x
optimizer = optim.SGD(model.parameters(), lr=0.01,weight_decay=0.01)
上次实践中,我们已经实现了权重初始化和正则化。
本身实践中,我们并不会再改动模型结构,而更侧重在同一结构下使用各种优化的效果。
首先,先回忆一下小批次,批量和随机梯度下降法的概念,它们的不同只针对批次大小。
- 随机梯度下降法SGD:每次迭代只使用一个样本,一个epoch中,有几个样本,就进行几次传播。
- 批量梯度下降法GD:每次迭代使用全部训练样本,一个epoch中,只进行一次传播。
- 小批次梯度下降法 Mini-GD:人为规定批次大小,一个epoch中,几个批次可以覆盖全部训练样本,就进行几次传播。
现在来展开几个小问题:
(1)PyTorch 封装三种梯度下降法的逻辑
首先,你可能发现了这样一个问题,我们之前不是一直使用的小批次下降法吗?
为什么代码里是 SGD?
optimizer = optim.SGD(model.parameters(), lr=0.01,weight_decay=0.01)
关于这个问题,实际上,PyTorch是用SGD整个代指了三种梯度下降法。
因为它们的不同只针对批次大小,更新参数的逻辑是不变的。
因此,这里的SGD实际上指的参数更新方式。
再想想,我们想应用这三种里的不同方式,是不是完全不必要封装三种方法?
因为它们的不同只有一个:批次大小。
所以,PyTorch 把划分不同批次大小封装在了数据集划分模块。
这部分内容在我们第一次用PyTorch设置整体框架这里:神经网络基础 课后习题和代码实践
直接挑出来,就是这里:
# 1.加载数据集
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
# 2.划分数据集大小
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
# 3.最后按大小设置数据迭代器
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
这是我们对整个数据集的设置,而哪一部分和我们的三种梯度下降法相关?
就是这句:
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
这里就是我们的训练集加载器。
再核心一点,哪个参数和我们的三种梯度下降法相关?
就是这个:
batch_size = 32
不难看出这个参数的意思就是批次大小,现在我们就是在以每批次使用32个样本进行训练和传播。
同理,我们想用SGD,那就是:
batch_size = 1
想用GD,那就是:
batch_size = train_size
知道了如何在PyTorch中使用不同批次大小梯度下降后,我们就来看看效果。
(2)三种梯度下降法的实际效果
还是把完整代码放在最后,我们来看看实际运行的效果。
要提前说明的是,因为硬件原因和让对比图更直观,我只把大批次设置为了256,大家理解原理就好,有兴趣可以自行尝试更大的批次效果。
我们来看看结果:
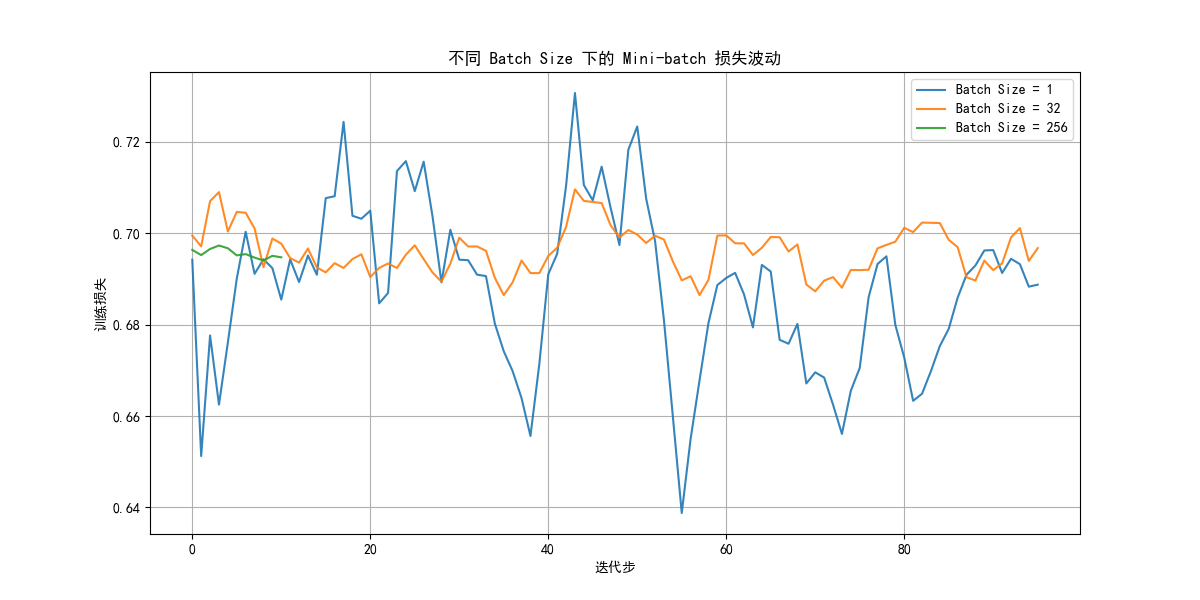
注意,这里的横轴单位是一个batch的迭代,不是一个epoch,这样我们才能看到批次大小的直接影响。
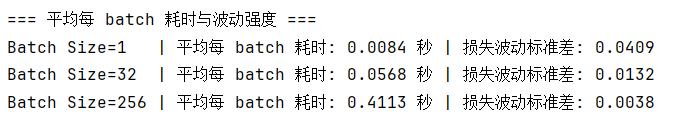
就像我们理论里说的一样:批次越小,波动性越大,反过来也是一样的。
这是因为一次迭代的参数更新只依赖该次梯度大小,而批次样本越少,批次间的差别就可能更大。
同时,批次越小,一批次训练的耗时就越少,这很直观,更少的数据量自然带来更快的计算。
再完善一点,你会发现大批次的曲线很短,这是因为它几次迭代就完成了所有样本的训练,还是我们在理论里提到的:批次越大,一个epoch中的迭代次数就越少。
这就是批次大小带来的影响。
批次越大,损失下降就更平稳。
但就像我最开始说的,当批次大小过大时,硬件就可能支持不了计算量。如何在成本能支持的批次量下实现更好的效果,就是我们后面了解的几种优化算法。
2.2 Momentum,RMSprop和Adam
不同于上面的只改变批次大小,这几种算法更改了参数更新的逻辑。因此也有不同的方法。
而这些不同的优化算法都被封装在优化器模块里。
现在我们固定批次大小为16,让波动大一些,来更好的看看优化效果。
来看看这几种算法的应用和对比。
(1)Pytorch中几种优化算法的应用
- 首先,这是原本的普通梯度下降法:
optimizer = optim.SGD(model.parameters(), lr=lr,weight_decay=0.01)
- 而这就是动量梯度下降法:
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=0.01)
你会发现它只是在SGD里增加了一个参数momentum=0.9,这叫动量项,0.9也就是平滑系数。
想一想,如果不使用这个参数,那在普通的SGD里,这个参数的默认值是不是就是0,代表只依赖当次梯度。
3. 再看看RMSprop:
optimizer = optim.RMSprop(model.parameters(), lr=lr, alpha=0.99, weight_decay=0.01)
首先它更改了方法名,而参数里的alpha=0.99,就代表梯度平方EMA的平滑系数,它的默认值就是0.99,可以省略。
4. 最后就是Adam:
optimizer = optim.Adam(model.parameters(),lr=lr,betas=(0.9,0.999),weight_decay=0.01)
betas就是设置一二阶矩平滑系数的参数,这里就是默认值,可以省略。
(2)应用结果对比
进行多次实验,来看一下其中一次的结果:
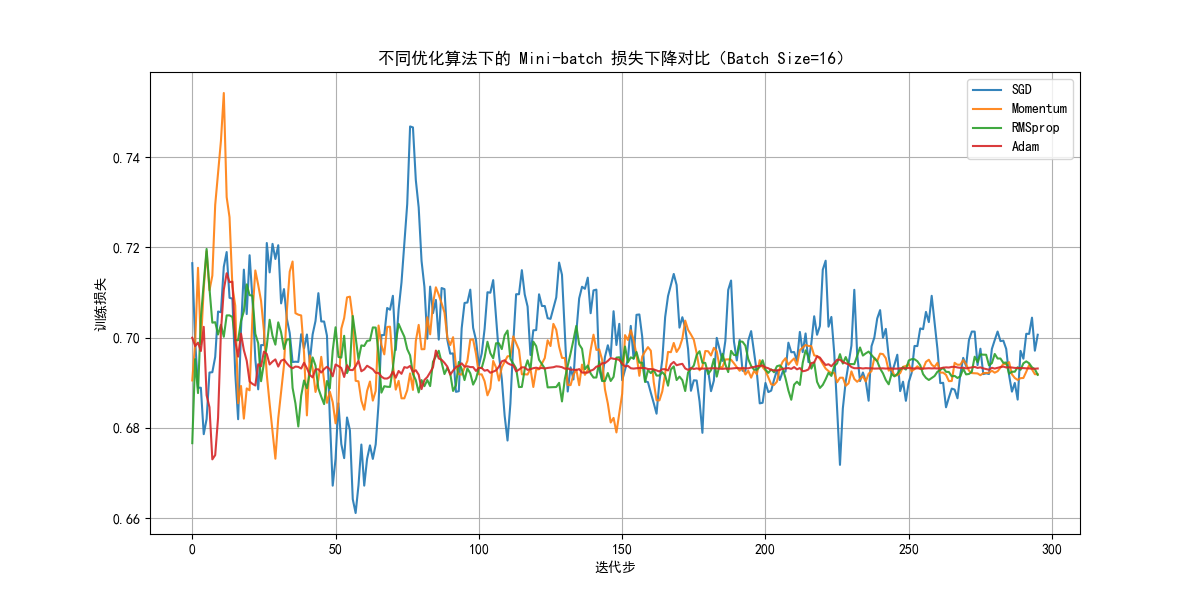
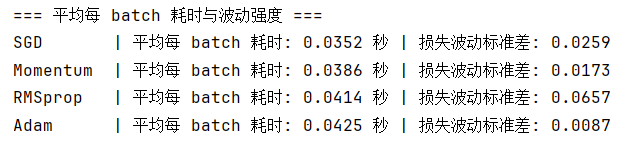
我们来看一下,首先波动性上 :$$RMSprop>SGD>Momentum>Adam$$
我们反过来,从小到大分析:
- Adam:
作为 Momentum + RMSprop 的集成者,Adam 同时考虑了 梯度的一阶矩(方向) 和 二阶矩(幅度)。
因此,Adam 的损失曲线在训练中表现为 波动最小且收敛较快。 - Momentum:
Momentum 仅平滑梯度方向,没有幅度自适应机制。
因此,它在方向震荡上较 SGD 有明显优势,但梯度幅度差异仍会导致一定波动。 - SGD(普通随机梯度下降):
- 每个 batch 都直接按当前梯度更新。
- 没有方向平滑,也没有步长自适应。
因此,你会发现它的波动性从始至终都相对较大,且收敛较慢。
- RMSprop:
作为一个新提出的优化算法,为什么多次实验中,他的平均波动都比SGD还大?
我们来看看图像,你会发现,RMSprop在初期的波动非常大。
因为它只使用二阶矩,在小批次(噪声平均更大)和没有方向信息(一阶矩)的前提下,可能会在噪声较大时更为敏感,就像对着一个噪声方向猛踩油门,下一次看到对的又飙回来。
而此时我们还没有很多批次来”平均“,就会让其在初期较大震荡。
但你会发现,适应初期后,它的收敛就会比SGD快很多。
最后还要强调一点,这种波动排序并不绝对,训练本身就存在一定的随机性,有时你甚至能看到SGD的效果比Adam好。
现在我们把范围扩大到epoch再进行几次实验,选择其中一次来看看损失下降效果:
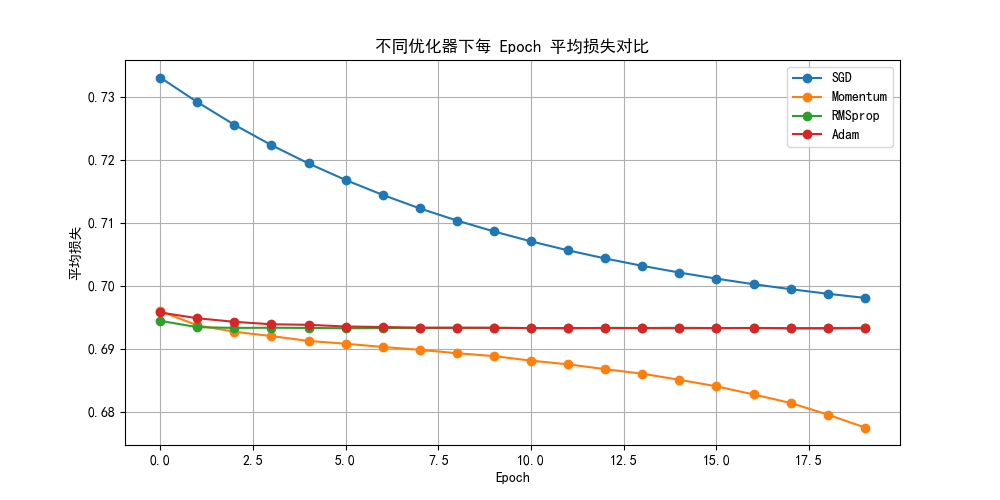
可以发现,几种优化算法的性能确实都高于SGD。
你会发现理应最好的Adam好像”卡住了“,这也是训练的随机性导致的,可能下一轮它就会跳出来,可能它会一直卡在这里。
总之,我们可以从平均收敛效果上看出几种优化算法的优劣,而这种优劣会随着数据量的增加而更加明显,但要实现好的拟合效果一定是各部分协作的效果,我们不可能说只凭优化部分来极大的增加拟合效果。
对于现在而言,一般在优化算法部分,Adam就是我们的默认选择。
3.附录
3.1 对比不同批次大小
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import init
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
import numpy as np
import time
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, _, _ = random_split(dataset, [train_size, val_size, test_size])
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.relu(self.hidden3(x))
x = self.relu(self.hidden4(x))
x = self.relu(self.hidden5(x))
x = self.relu(self.hidden6(x))
x = self.sigmoid(self.output(x))
return x
def train_and_record(batch_size, epochs=3):
loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
model = NeuralNetwork().to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=0.01)
batch_losses = []
start_time = time.time()
for epoch in range(epochs):
model.train()
for images, labels in loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
batch_losses.append(loss.item())
avg_time = (time.time() - start_time) / (epochs * len(loader))
return batch_losses, avg_time
batch_sizes = [1, 32, 256]
results = {}
times = {}
print("开始训练并记录每个 batch 的损失...")
for bs in batch_sizes:
print(f"\n训练 batch_size={bs} ...")
losses, avg_t = train_and_record(bs, epochs=3)
results[bs] = losses
times[bs] = avg_t
print(f"batch_size={bs} 平均每 batch 时间: {avg_t:.4f} 秒")
max_points = 100 #统一可视化的迭代步数
aligned_losses = {}
for bs, losses in results.items():
if len(losses) > max_points:
idx = np.linspace(0, len(losses)-1, max_points).astype(int)
aligned_losses[bs] = [losses[i] for i in idx]
else:
aligned_losses[bs] = losses
def smooth(data, window=5):
if len(data) < window:
return data
return np.convolve(data, np.ones(window)/window, mode='valid')
# 绘制对比图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12,6))
for bs in batch_sizes:
smoothed = smooth(aligned_losses[bs], window=5)
plt.plot(smoothed, label=f'Batch Size = {bs}', alpha=0.9)
plt.title("不同 Batch Size 下的 Mini-batch 损失波动")
plt.xlabel("迭代步")
plt.ylabel("训练损失")
plt.legend()
plt.grid(True)
plt.show()
#输出
print("\n=== 平均每 batch 耗时与波动强度 ===")
for bs in batch_sizes:
std = np.std(results[bs])
print(f"Batch Size={bs:<3} | 平均每 batch 耗时: {times[bs]:.4f} 秒 | 损失波动标准差: {std:.4f}")
3.2 对比不同优化算法
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import init
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
import numpy as np
import time
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, _, _ = random_split(dataset, [train_size, val_size, test_size])
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.relu(self.hidden3(x))
x = self.relu(self.hidden4(x))
x = self.relu(self.hidden5(x))
x = self.relu(self.hidden6(x))
x = self.sigmoid(self.output(x))
return x
def train_and_record(optimizer_type, batch_size=16, epochs=20, lr=0.001):
loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
model = NeuralNetwork().to(device)
criterion = nn.BCELoss()
if optimizer_type == 'SGD':
optimizer = optim.SGD(model.parameters(), lr=lr, weight_decay=0.01)
elif optimizer_type == 'Momentum':
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=0.01)
elif optimizer_type == 'RMSprop':
optimizer = optim.RMSprop(model.parameters(), lr=lr, alpha=0.99, weight_decay=0.01)
elif optimizer_type == 'Adam':
optimizer = optim.Adam(model.parameters(), lr=lr, betas=(0.9,0.999), weight_decay=0.01)
batch_losses = []
epoch_losses = [] # 每 epoch 平均损失
start_time = time.time()
for epoch in range(epochs):
model.train()
epoch_loss = 0.0
for images, labels in loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
batch_losses.append(loss.item())
epoch_loss += loss.item()
epoch_losses.append(epoch_loss / len(loader)) # 平均每个 epoch 的损失
avg_time = (time.time() - start_time) / (epochs * len(loader))
return batch_losses, epoch_losses, avg_time
optimizers = ['SGD', 'Momentum', 'RMSprop', 'Adam']
results = {}
epoch_results = {}
times = {}
print("开始训练并记录不同优化器的损失...")
for opt_name in optimizers:
print(f"\n 训练优化器={opt_name} ...")
losses, epoch_losses, avg_t = train_and_record(opt_name)
results[opt_name] = losses
epoch_results[opt_name] = epoch_losses
times[opt_name] = avg_t
print(f"{opt_name} 平均每 batch 时间: {avg_t:.4f} 秒")
max_points = 300
aligned_losses = {}
for opt_name, losses in results.items():
if len(losses) > max_points:
idx = np.linspace(0, len(losses)-1, max_points).astype(int)
aligned_losses[opt_name] = [losses[i] for i in idx]
else:
aligned_losses[opt_name] = losses
def smooth(data, window=5):
if len(data) < window:
return data
return np.convolve(data, np.ones(window)/window, mode='valid')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12,6))
final_losses = {}
for opt_name in optimizers:
smoothed = smooth(aligned_losses[opt_name], window=5)
plt.plot(smoothed, label=opt_name, alpha=0.9)
final_losses[opt_name] = smoothed[-1] if len(smoothed) > 0 else np.nan
plt.title("不同优化算法下的 Mini-batch 损失下降对比(Batch Size=16)")
plt.xlabel("迭代步")
plt.ylabel("训练损失")
plt.legend()
plt.grid(True)
plt.show()
plt.figure(figsize=(10,5))
for opt_name in optimizers:
plt.plot(epoch_results[opt_name], marker='o', label=opt_name)
plt.title("不同优化器下每 Epoch 平均损失对比")
plt.xlabel("Epoch")
plt.ylabel("平均损失")
plt.legend()
plt.grid(True)
plt.show()
#输出
print("\n=== 平均每 batch 耗时与波动强度 ===")
for opt_name in optimizers:
std = np.std(results[opt_name])
print(f"{opt_name:<9} | 平均每 batch 耗时: {times[opt_name]:.4f} 秒 | 损失波动标准差: {std:.4f}")



 浙公网安备 33010602011771号
浙公网安备 33010602011771号