从点预测到分布建模:小红书-EGMN在视频观看时长预测中的方法与实践
从点预测到分布建模:小红书-EGMN在视频观看时长预测中的方法与实践
原文:https://arxiv.org/pdf/2508.12665
一、引言:问题背景与研究动机
在短视频推荐系统中,观看时长(Watch Time)被广泛视为衡量用户满意度与内容质量的核心信号之一。与点击、点赞等离散反馈不同,观看时长是一个连续变量,既能反映用户是否产生兴趣,又能刻画兴趣强弱程度,因此在排序与收益建模中具有不可替代的地位。
然而,从建模角度看,观看时长预测本质上是一个高难度的回归问题。一方面,其取值范围跨度大、分布极不均匀;另一方面,用户与视频的交互行为在不同层面呈现出显著差异。传统方法通常通过标签归一化或将回归问题转化为分类问题来降低难度,但这些做法往往以牺牲绝对时长信息或引入离散化误差为代价,难以从根本上解决问题。
本文关注的一篇工作提出了一个关键视角:观看时长预测的核心困难并不完全来自模型能力不足,而是来自对标签分布结构认识不足。作者基于真实工业数据,对观看时长在不同粒度下的分布特性进行了系统分析,并据此提出了 Exponential-Gaussian Mixture Network(EGMN),通过显式的分布建模来统一刻画粗粒度偏斜与细粒度多样性,从而提升预测精度与稳定性。
二、问题分析:多粒度观看时长分布特性
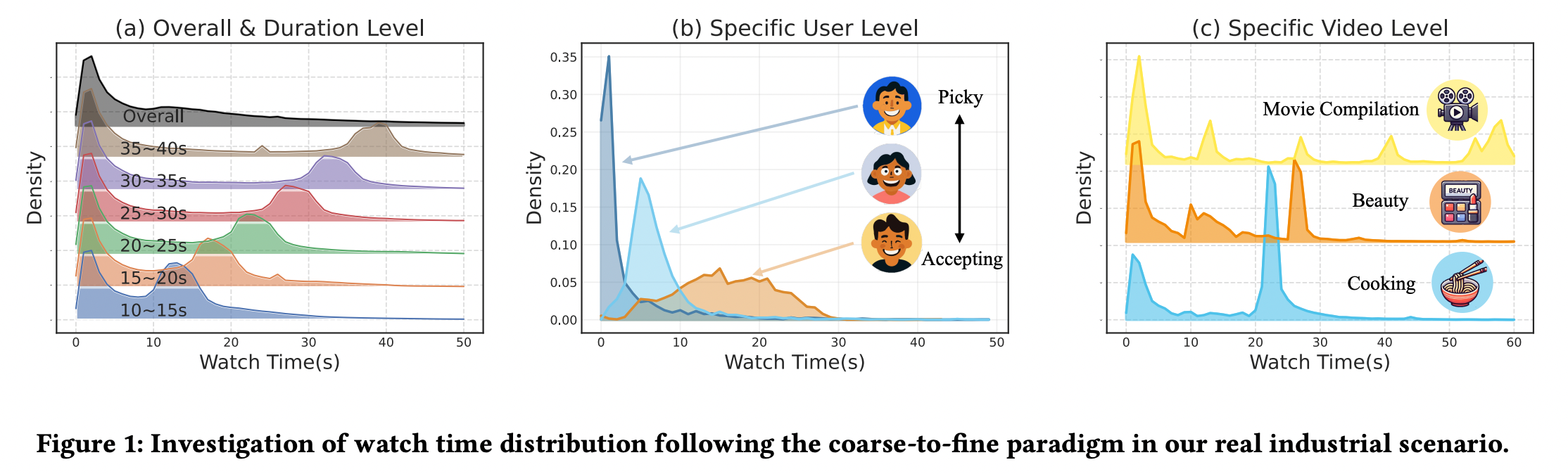
论文首先从数据分布角度出发,对短视频观看时长进行了由粗到细的多粒度分析,这一步是方法设计的关键基础。
在整体层面(Overall Level),观看时长分布呈现出极强的右偏特性,零附近存在高度集中的概率质量。这一现象主要由“快速划走”行为导致,即用户在极短时间内判断内容不感兴趣并立即跳过。这类行为数量庞大,使得整体分布在低时长区域高度拥挤。
在视频时长分组层面(Duration Level),观看时长分布开始呈现双峰或多峰结构。对于同一时长区间的视频,一部分用户迅速退出,而另一部分用户则可能接近完整观看。这说明即便控制了视频长度,用户行为仍然具有明显分化。
进一步下钻到用户层面(User Level),分布差异更加显著。有些用户表现为“挑剔型”,大多数视频被快速跳过;而另一些用户则更为“宽容”,倾向于对推荐内容进行更充分的观看。这种个体差异意味着统一的分布假设在细粒度层面难以成立。
在视频层面(Video Level),观看时长分布往往呈现多模态结构。例如,剧情分段明显的视频在若干关键节点存在集中退出点,而具有强吸引力的视频则可能出现重复观看现象。这种多模态特性反映了内容结构与用户行为的复杂耦合。
综合上述分析,作者将观看时长预测面临的挑战归纳为两点:其一,粗粒度层面存在由快速划走导致的强偏斜分布;其二,细粒度层面存在由用户与内容异质性引发的分布多样性。这两种特性需要在同一建模框架下被同时刻画。
通常做法:使用 MSE 做观看时长回归,并不仅仅是在最小化预测误差,而是在隐式地假设观看时长在条件于特征后服从一个同方差的单峰高斯分布。该假设与短视频场景中普遍存在的快速划走、长尾行为和多模态观看模式严重不符,导致模型在理论上只能学习条件均值,在实践中难以刻画真实的用户–视频交互结构。
三、方法总览:Exponential-Gaussian Mixture 建模思想
针对上述挑战,论文提出不再回避复杂分布,而是直接对观看时长的生成分布进行建模。核心假设是:短视频观看时长可以被视为由不同潜在行为模式混合生成的随机变量。
具体而言,作者提出 Exponential-Gaussian Mixture(EGM)分布假设。其中,指数分布用于刻画快速划走行为所带来的强偏态特性,而若干高斯分布用于刻画不同用户–视频交互模式下的观看时长波动。指数分量在低时长区域具有较高概率密度,高斯分量则在中高时长区域提供更灵活的形状表达能力。
这种混合分布的设计本质上是一种多粒度统一建模思路:指数分布负责解释全局层面的集中偏斜,高斯分布负责吸收细粒度层面的多样性。通过在一个统一的概率框架下联合建模,模型无需依赖人为的标签变换或任务拆解。
四、模型结构:Exponential-Gaussian Mixture Network(EGMN)
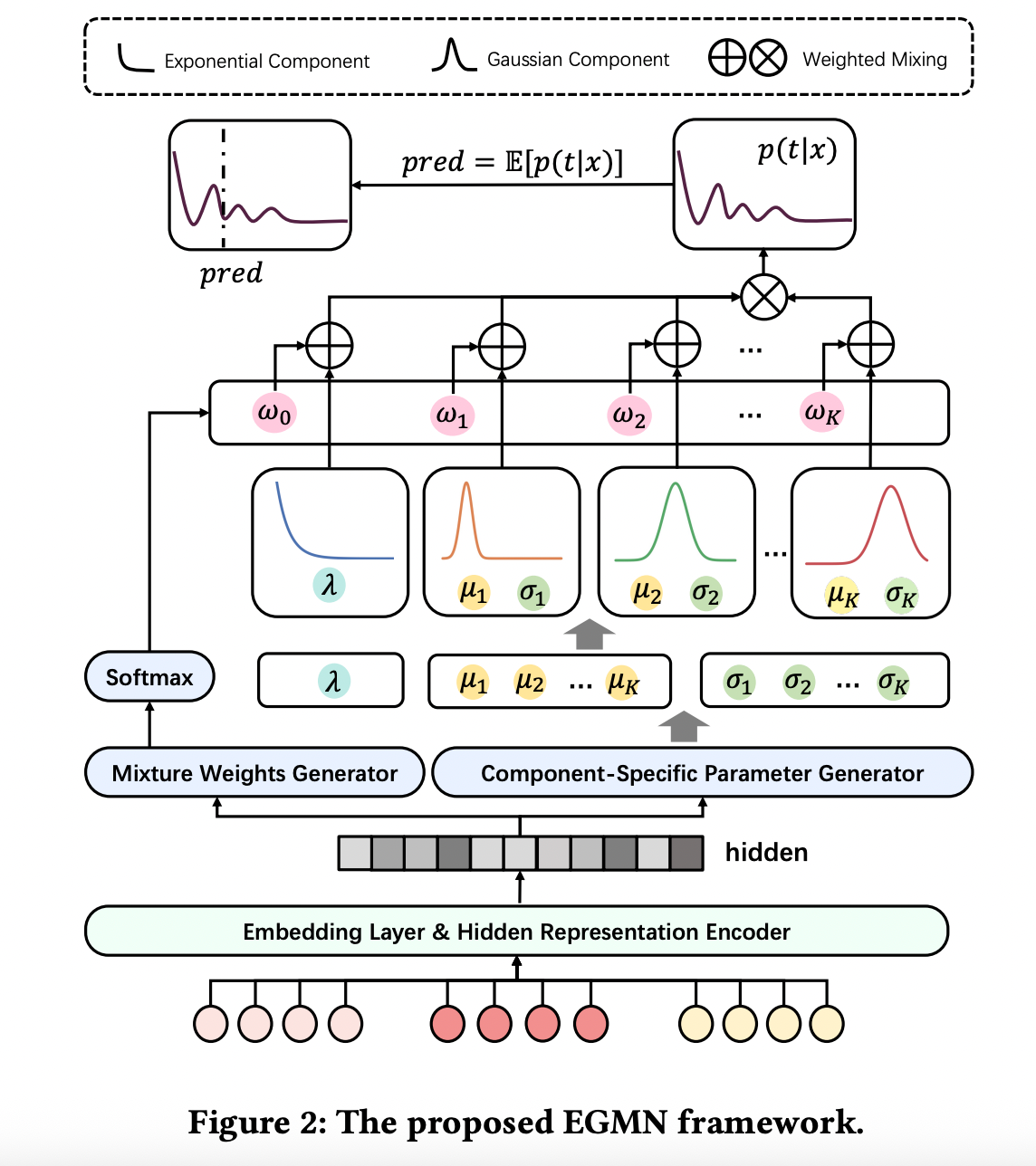
为了在神经网络框架下参数化 EGM 分布,论文提出了 Exponential-Gaussian Mixture Network。整体结构可以分为两个主要模块。
第一部分是隐藏表示编码器。模型接收用户特征、视频特征及上下文特征作为输入,通过多层神经网络映射到一个共享的隐藏表示空间。该表示被视为对当前用户–视频交互状态的高层抽象,是后续分布参数生成的共同基础。
第二部分是混合分布参数生成模块。基于共享隐藏表示,模型分别预测指数分布的参数、高斯分布各分量的均值与方差,以及各分量对应的混合权重。为了保证混合权重满足概率约束,通常通过 softmax 形式进行归一化。
这种结构设计的关键在于“共享表示、分头建模”。共享表示确保不同分布分量感知到一致的语义上下文,而分头输出则赋予模型在分布形态上的灵活性。
五、EGM 分布的参数化与数学形式
形式化地,EGM 分布可以表示为指数分布与若干高斯分布的加权混合。其概率密度函数为

其中 \(t\) 表示观看时长,\(x\) 表示输入特征,\(\pi_k\) 为混合权重,满足 \(\sum_k \pi_k = 1\)。
指数分布部分通过参数 \(\lambda\) 控制衰减速度,用于拟合快速划走行为;高斯分布部分通过 \((\mu_k,\sigma_k)\) 刻画不同观看模式下的集中趋势与离散程度。
具体的实现

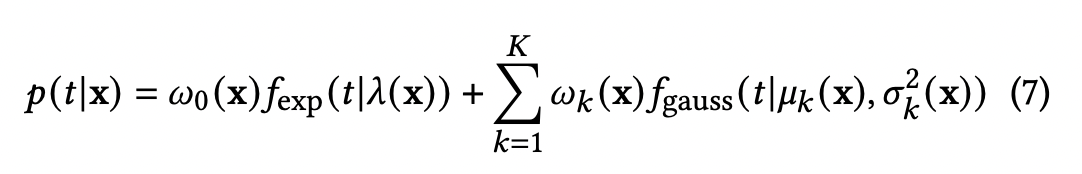
在推理阶段,模型并不直接输出单一时长值,而是输出一个完整的参数化分布。最终用于排序或回归评估的预测值通常取该分布的期望
六、训练目标
EGMN 的训练目标基于以下三个损失函数。
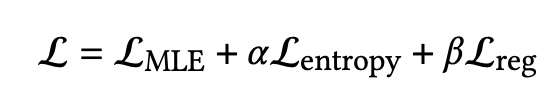
alpha默认0.1,beta默认1.0
1.最大似然估计损失——Maximum Likelihood Estimation Loss
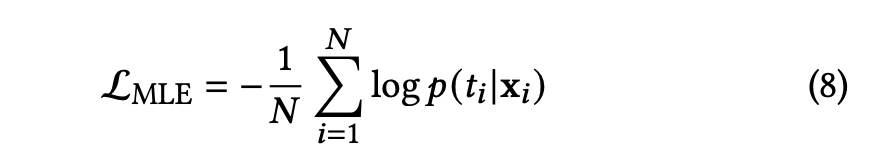
更进一步:
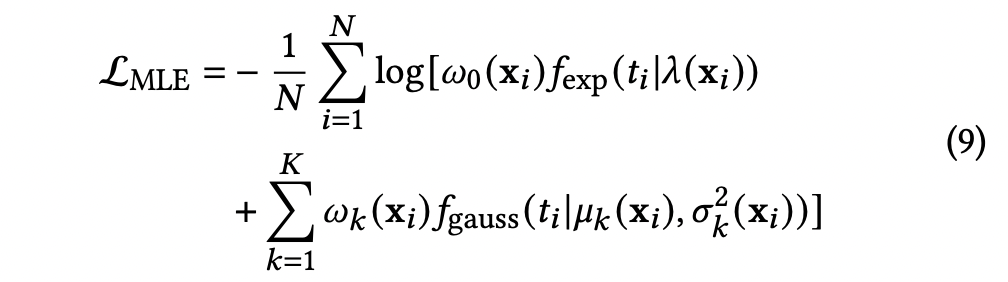
该损失函数通过鼓励模型在真实观看时长处赋予更高的概率密度,引导 EGMN 学习不同内容类型和观看上下文下的用户参与行为分布。
2.熵最大化损失——Entropy Maximization Loss
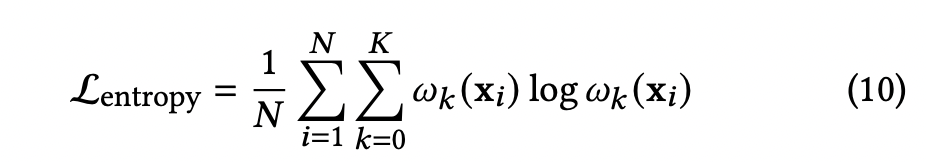
为防止训练过程中模型退化为仅使用单一分布分量。最小化该损失等价于最大化混合权重分布的熵,从而鼓励模型在必要时合理利用多个分量,而非将全部概率质量集中到单一分量上。这一机制对于保持模型刻画观看时长多模态分布的能力至关重要
Regression Loss
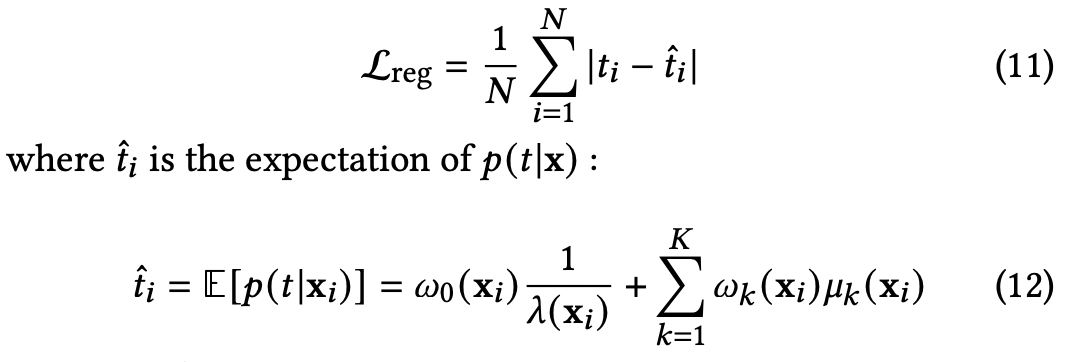
为保证模型在绝对数值预测上的性能,引入基于分布期望的回归损失,在评估阶段,y^i被作为最终的观看时长预测值。通过最小化 Lreg,模型在保持分布建模能力的同时,也被显式地约束生成准确的数值预测。
七、输入输出流程的端到端解析
在实际推理时,模型输入包括用户画像特征、视频内容特征以及上下文信息。输入首先经过编码器生成隐藏表示,随后由参数生成模块输出 EGM 分布的全部参数。
模型输出并非单点预测,而是一个完整的观看时长分布。这一分布既可用于计算期望值作为排序分数,也可用于下游风险控制或不确定性分析,具有更强的表达能力。
八、实验结果与效果验证
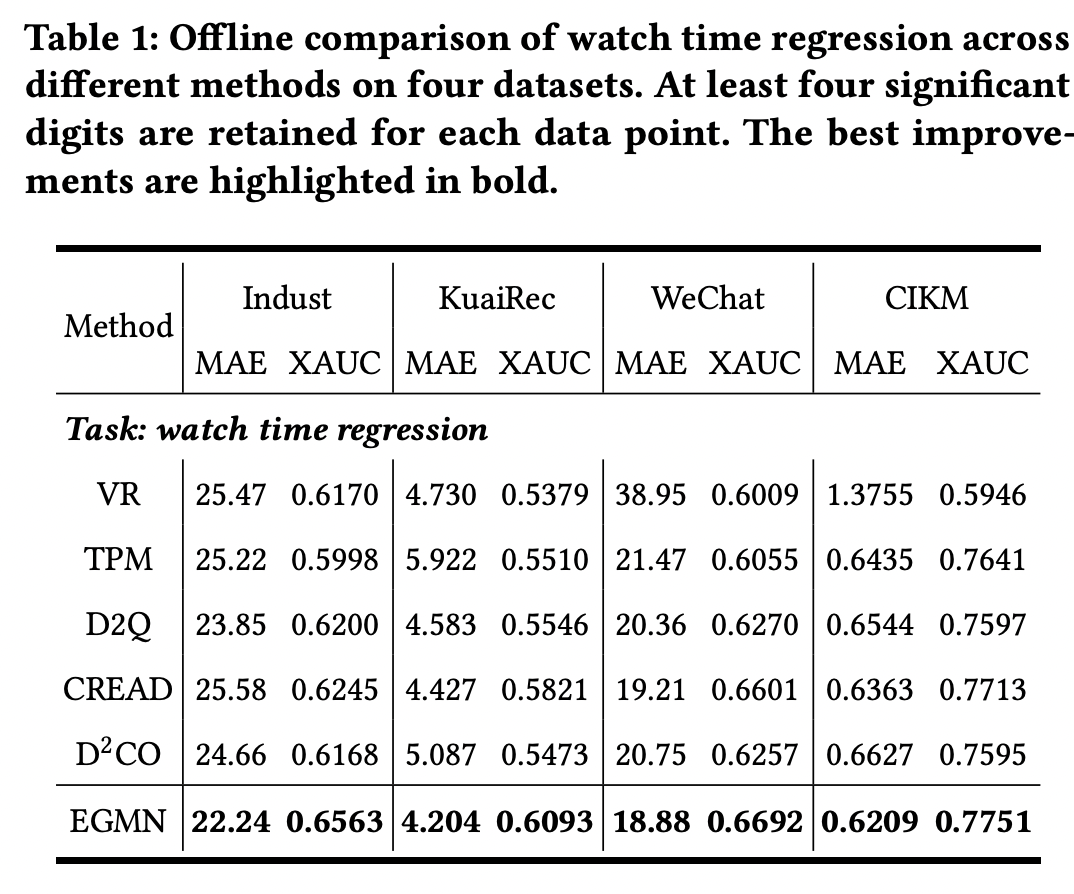
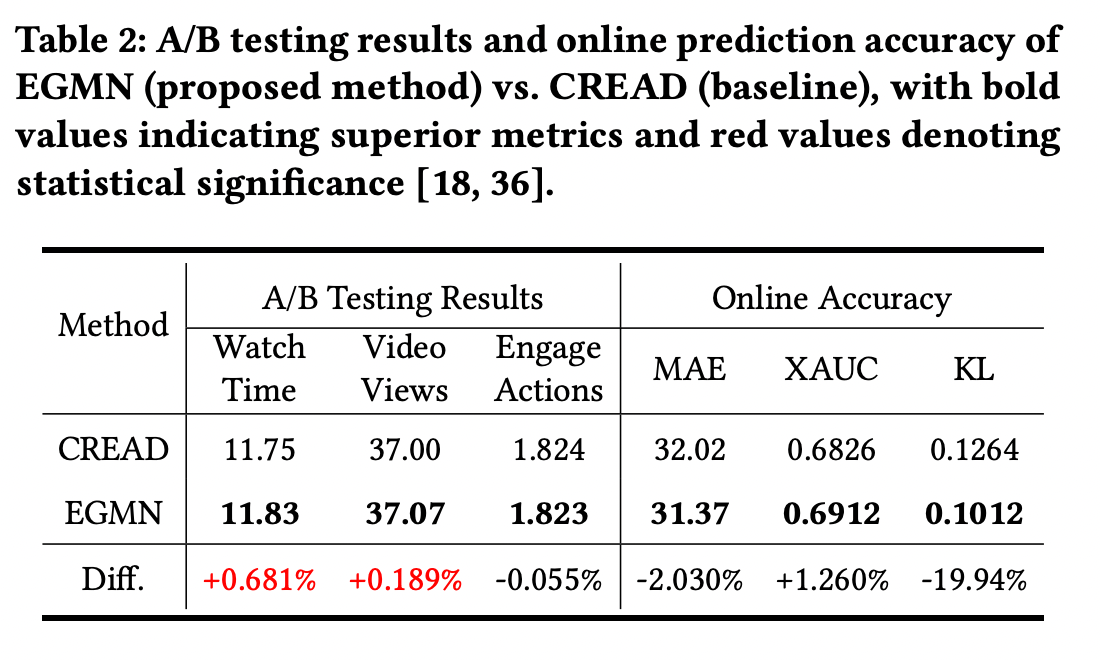
实验结果表明,EGMN 在多个公开数据集及真实线上场景中均优于传统回归与分类方法。尤其在长尾区域和多模态分布场景下,其分布拟合能力显著提升。
消融实验进一步验证了指数分量与高斯分量各自的必要性,说明单一分布假设难以覆盖多粒度行为特征。
九、方法优缺点与适用场景分析
EGMN 的主要优势在于显式建模标签分布,能够自然吸收偏斜与多样性,对复杂用户行为具有较强鲁棒性。但其代价是模型复杂度与训练成本的上升,同时对分布假设的合理性存在一定依赖。该方法特别适用于观看时长、停留时长等连续行为信号显著偏态且多模态的推荐或广告场景。
本文通过对观看时长多粒度分布特性的深入分析,提出了 EGMN 这一分布感知建模框架。其核心价值在于将“预测值”问题上升为“分布建模”问题,为推荐系统中连续反馈信号的建模提供了一条具有普适意义的思路。
EGMN模型源代码(附上代码注释)
import torch
import torch.nn as nn
import torch.distributions as D
import torch.nn.functional as F
import numpy as np
from model.layers import FactorizationMachine, MultiLayerPerceptron, DurationMultiLayerPerceptron
class EGMN(torch.nn.Module):
def __init__(self, description, embed_dim, share_mlp_dims, output_mlp_dims, dropout):
super().__init__()
# "ctn"(连续特征)、"seq"(序列特征)或"spr"(稀疏特征)
self.features = {name: (size, type) for name, size, type in description if (type in ["ctn", 'seq', 'spr'])}
# 将实际模型构建逻辑委托给build方法
self.build(embed_dim, share_mlp_dims, output_mlp_dims, dropout)
# 实际模型构建逻辑
def build(self, embed_dim, share_mlp_dims, output_mlp_dims, dropout):
# torch.nn.ModuleDict()专门用于存储多个 nn.Module 对象(神经网络层)的容器,适合存储包含可学习参数的完整网络层(如 Linear, Embedding 等)
# torch.nn.ParameterDict()专门用于存储多个 nn.Parameter 对象的容器,于直接管理原始参数(当不需要完整层封装时)
self.emb_layer = torch.nn.ModuleDict()
self.ctn_emb_layer = torch.nn.ParameterDict()
self.ctn_linear_layer = torch.nn.ModuleDict()
embed_output_dim = 0
# name, (size, type) == {特征名: (特征大小, 特征类型)}
for name, (size, type) in self.features.items():
if type == 'spr':
self.emb_layer[name] = torch.nn.Embedding(size, embed_dim)
embed_output_dim += embed_dim
elif type == 'ctn':
self.ctn_linear_layer[name] = torch.nn.Linear(1, 1, bias=False)
embed_output_dim += 1
elif type == 'seq':
self.emb_layer[name] = torch.nn.Embedding(size, embed_dim)
embed_output_dim += embed_dim
else:
raise ValueError('unkown feature type: {}'.format(type))
self.share_mlp = MultiLayerPerceptron(embed_output_dim, share_mlp_dims, dropout, output_layer=False)
hidden_dim = share_mlp_dims[-1]# + 1
# 指数分布参数分支(快滑峰),输出为单个参数lambda
self.lambda_layer = nn.Sequential(
nn.Linear(hidden_dim, 1),
nn.Softplus(beta=0.5)
)
# comp_num表示高斯分布的个数
comp_num = 10
# 输出comp_num+1的权重系数
self.mixture_logits = nn.Linear(hidden_dim, comp_num+1)
# 输出comp_num个高斯分布的均值u和sigma
self.gauss_mu = nn.Sequential(
nn.Linear(hidden_dim, comp_num),
# MultiLayerPerceptron(hidden_dim, output_mlp_dims, dropout, output_layer=True),
nn.Softplus()
)
self.gauss_sigma = nn.Sequential(
nn.Linear(hidden_dim, comp_num),
# MultiLayerPerceptron(hidden_dim, output_mlp_dims, dropout, output_layer=True),
nn.Softplus()
)
return
def init(self):
for param in self.parameters():
torch.nn.init.uniform_(param, -0.01, 0.01)
def forward(self, x_dict):
linears = [] # 存储处理后的连续特征
embs = [] # 存储处理后的稀疏特征
for name, (_, type) in self.features.items():
x = x_dict[name]
# 处理单值稀疏特征
if type == 'spr':
embs.append(self.emb_layer[name](x).squeeze(1))
# 处理连续特征
elif type == 'ctn':
linears.append(self.ctn_linear_layer[name](x))
# 处理多值稀疏特征(历史行为序列)
elif type == 'seq':
seq_emb = self.emb_layer[name](x)
seq_mask = torch.unsqueeze(x_dict["{}mask".format(name)], dim=2)
# mask将0值屏蔽,将已交互物品的向量进行相加后,再除以交互物品的个数(average pooling)
embs.append(torch.sum(seq_emb * seq_mask, dim=1) / torch.sum(seq_mask, dim=1))
else:
raise ValueError('unkwon feature: {}'.format(name))
# 拼接,形成输入x,[batchsize, dim]
emb = torch.concat(embs + linears, dim=1)
# 共享底座隐藏层,hidden = [batchsize, share_mlp[-1] ]
hidden = self.share_mlp(emb)
# hidden = torch.concat([hidden, engage_pred.view(-1, 1)], dim=1)
# 指数分布 lambda_
lambda_ = self.lambda_layer(hidden) + 1e-6
# 权重:[batch, componet+1]
pi = self.mixture_logits(hidden) # [batch, componet+1]
# 高斯分布mu,sigma
mu = self.gauss_mu(hidden) + 1/lambda_ # [batch, component]
# mu = torch.cumsum(mu, dim=1) + 1/lambda_
sigma = self.gauss_sigma(hidden) + 1e-6 # [batch, component]
return pi, lambda_, mu, sigma
def loss(self, y_true, pi, lambda_, mu, sigma, duration):
batch_size = y_true.shape[0]
y_true = y_true.view(-1, 1)
# 指数分布(快滑峰)
exp_dist = D.Exponential(rate=lambda_.view(-1))
# 指数分布的log_prob,[batch, 1],输入的y_true是实际标签,输出的是对应的概率
log_prob_short = exp_dist.log_prob(y_true.view(-1)).view(batch_size, 1)
# 高斯分布
log_prob_all = []
# mu, sigma = [batch, component]
for comp_idx in range(mu.shape[1]):
normal_dist = D.Normal(loc=mu[:, comp_idx], scale=sigma[:, comp_idx]) # 高斯分布
trunc_min = torch.zeros_like(mu[:, comp_idx]) # 形状为[batch, 1]的0矩阵
# cdf概率密度函数,计算每个样本在截断点(0)右侧的概率,[batch, 1]
prob_long = 1.0 - normal_dist.cdf(trunc_min)
# 因为当y_true小于u时,不应该有对应的概率值,因此需要将截断。再进行归一化,换算为log概率,也就是减去截断点0右侧的概率
log_prob = normal_dist.log_prob(y_true.view(-1)) - torch.log(prob_long + 1e-6)
# 第一个项:每个样本在真实值处的对数概率
# 第二个项:截断归一化因子的对数, [batch, comp_nm]
log_prob_all.append(log_prob.view(-1, 1))
# 将指数分布对数概率与component个高斯分布对数概率相加
log_prob_all = torch.concat([log_prob_short] + log_prob_all, dim=1)
# 混合概率,权重pi归一化,[batch, component+1]
mix_probs = torch.softmax(pi, dim=1)
# sample_w = (1 + y_true * duration)
# sample_w = torch.where(y_true * video_durations.view(-1, 1) < 0.005, 0.5 * torch.ones_like(y_true), torch.ones_like(y_true) )
# nll loss,核心训练目标是最大化观测到的观看时长在 EGM 分布下的似然
# 对权重取对数,[batch, component+1]
log_mix_probs = torch.log_softmax(pi, dim=1)
# 对所有分量乘以权重求和,得到最终的对数概率
total_log_prob = torch.logsumexp(
log_mix_probs + log_prob_all,
dim=1, keepdim=True
)
nll_loss = -torch.mean(total_log_prob)
# reconstruction loss,为保证模型在绝对数值预测上的性能,本文引入基于分布期望的回归损失
pi = torch.softmax(pi, dim=1)
# 用于排序或回归评估的预测值通常取该分布的期望
pred = torch.sum(pi * torch.concat([1/lambda_, mu], dim=1), dim=1, keepdim=True)
reg_loss = F.l1_loss(pred, y_true.float())
# mixture entropy loss,防止训练过程中模型退化为仅使用单一分布分量,本文在混合权重上引入熵最大化正则项
entropy_loss = torch.sum(mix_probs * torch.log(mix_probs + 1e-6), dim=1).mean()
return nll_loss, reg_loss, entropy_loss
def get_quantile(self, pi, lambda_, mu, sigma, tau=0.5):
exp_dist = D.Exponential(rate=lambda_.view(-1, 1))
norm_dist_list = []
for comp_idx in range(mu.shape[1]):
normal_dist = D.Normal(loc=mu[:, comp_idx:comp_idx+1], scale=sigma[:, comp_idx:comp_idx+1])
norm_dist_list.append(normal_dist)
try_list = torch.arange(0, 1, 0.0001).view(1, -1).to(pi.device)
cdf = exp_dist.cdf(try_list.view(1, -1))
for norm_dist in norm_dist_list:
cdf += norm_dist.cdf(try_list.view(1, -1))
try_list = try_list.view(-1)
idx = (cdf < tau).to(torch.int8).sum(dim=1)
return try_list[idx]
def predict(self, x):
with torch.no_grad():
pi, lambda_, mu, sigma = self.forward(x)
pi = torch.softmax(pi, dim=1)
# 用于排序或回归评估的预测值通常取该分布的期望
return torch.sum(pi * torch.concat([1/lambda_, mu], dim=1), dim=1)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号