基本线段树

线段树

1.概念理解

如图

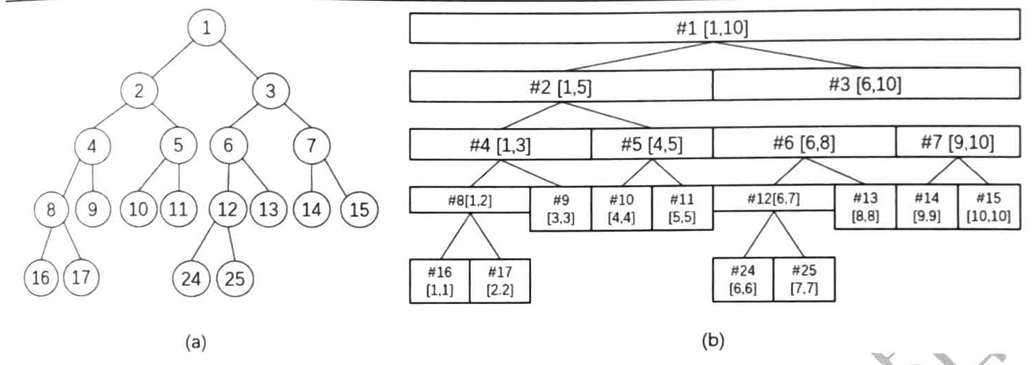
线段树作为一个数据结构，通常用来优化区间操作，如一个区间的数同时加减，乘除，求和等

如图中对数组1-4进行+3，那么我只需对#4节点+3和对#10节点+3

当要查询1-4之和时便只需查询#4与#10之和

同时在修改时还会给父节点添加标记（用来向下传递）与向上传递数据，以便后续的访问

2.代码实现

1.初始操作

#include<bits/stdc++.h>
using namespace std;
int maxn=10001;
int a[maxn];//记录初始数组
struct node{
	int l,r;//左右节点
    int w;//数值
    int tag;//标记
} tree[maxn*4]//采用结构体存储线段树		

2.建树

void pushup(int p){
	tree[p].w=tree[p*2].w+tree[p*2+1].w
}
void build(int p,int l,int r){
	if(l==r){//到达叶子节点
		tree[p].w=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(p*2,l,mid);
    build(P*2+1,mid+1,r);
    pushup(p);
}//这里采用递归建树

3.区间加

这里便需要用到懒标记Lazytag 用来记录修改的信息

当递归至一个被完全包含的区间时，在这个区间上打一个延迟标记，记录每个数都需要被加上某个数，然后直接修改该结点的区间和并返回，不再向下递归。当新访问到一个结点时，先将延迟标记下放到子结点，然后再进行递归。

void maketag(int p,int len,int  x){
	tree[p].tag+=x;
    tree[p].w+=len*x;
}

接着便是下放lazytag 的pushdown

void pushdown(int p,int l,int r){
	int mid=(l+r)>>1;
    maketag(p*2,mid-l+1,tree[p].tag);
    maketag(p*2+1,r-mid,tree[p].tag);//给左右子树都打上懒标记
    tree[p].tag=0;
}

最后便是区间加

void modify(int p,int l,int r,int ql,int qr,int x){
	if(ql<=l&&qr>=r)maketag(p,r-l+1,x);//完全包含直接打标记
    else if(!(l>qr||r<ql)){
    	pushdown(p,l,r);//先将当前标记下传再递归修改
        int mid=(l+r)>>1;
        modify(p*2,l,mid,ql,qr,x);
        modify(p*2+1,mid+1,r,ql,qr,x);
        pushup(p);//最后统计左右节点
    }
}

4.区间查询

int query(int p,int l,int r,int ql,int qr){//l,r代表正在遍历的区间;ql,qr代表要查询的区间
	if(ql<=l&&qr>=r)return tree[p].w;
    if(l>qr||r<ql)return 0;
    int mid=(l+r)>>1;
    pushdown(p,l,r);//查询时也要下放Lazytag
    return query(p*2,l,mid,ql,qr)+query(p*2+1,mid+1,r,ql,qr);
}

Tips:笔记均用int,做题时根据实际情况改变变量类型

例题

P3373 【模板】线段树 2

题目要求：区间乘，区间加，区间和查询

题解：增加一个区间乘的tag与修改

void maketag_multipy(int p,long long x){
	(tree[p].w*=x)%=m;
	(tree[p].tag_multipy*=x)%=m;
	(tree[p].tag_plus*=x)%=m;//区间加的tag也要乘，否则下传标记时会漏
}

同时注意pushdown时先乘法后加法

P3870 [TJOI2009] 开关

题目概述：区间异或与求和

修改一下标记函数与pushdown

void maketag(int p,int len){
	tree[p].w=len-tree[p].w;
	tree[p].tag^=1; 
}
void pushdown(int p,int l,int r){
	if(tree[p].tag==0)return; 
	int mid=(l+r)>>1;
	maketag(p*2,mid-l+1);
	maketag(p*2+1,r-mid);
	tree[p].tag=0;
}

异或标记可向下传递

同时要注意两次0 ^ 1 ^ 1=0，相当于没有改变