Dijkstra

Dijkstra

例题：P4779 【模板】单源最短路径（标准版）

给定一个 \(n\) 个点，\(m\) 条有向边的带非负权图，请你计算从 \(s\) 出发，到每个点的距离。

数据保证你能从 \(s\)​ 出发到任意点。

输入格式

第一行为三个正整数 \(n, m, s\)。
第二行起 \(m\) 行，每行三个非负整数 \(u_i, v_i, w_i\)，表示从 \(u_i\) 到 \(v_i\) 有一条权值为 \(w_i\) 的有向边。

输出格式

输出一行 \(n\) 个空格分隔的非负整数，表示 \(s\)​ 到每个点的距离。

过程解析

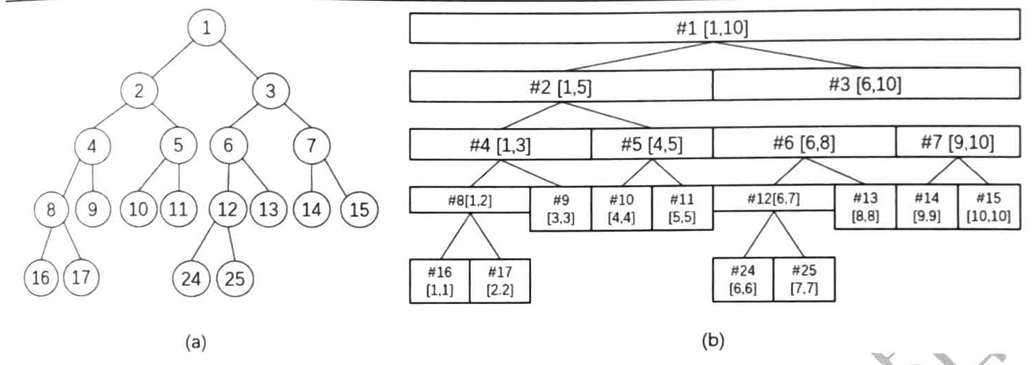
用一个dis数组记录起点到各个点的最短路径长度

(1)先将各个点的dis初始化为inf,起点初始化0

(2)松弛操作:对于一条从顶点u到v，长度为w的边，如果dis[u]+w<dis[v],那么dis[v]=dis[u]+w

​ 从起点①出发，松弛所有出边，并将①标记（标记代表这个点的dis不再改变）状态如图(b)

(3)再松弛过的点中选取dis值最小的点，如图(c),此时为点②(选取②才可优化其它点dis)

​ 将②的所有出边松弛并标记②

(4)重复操作④，③

存边：链式前向星

将每个顶点出发的所有边以一个链表的形式保存

next数组代表下一项的下标

head数组记录起点下标

struct L{
    int to,next,length;
}bian[maxn];
int head[maxn],k;
void(int u,int v,int w){
    bian[++k].to=v;
    bian[k].length=w;
    bian[k].next=head[u];//下一条边
    head[u]=k;//下标
}

例如对于①有编号为1，2，3的三条边

bian[1].next=0;

head[1]=1;

bian[2].next=1;

head[1]=2;

bian[3].next=2;

head[1]=3;

在遍历时则与存储顺序相反，3-->2-->1

优先队列

为了优化从出边的点中找出dis最小的点，采用优先队列

struct P{
	int dis,id;//id即点的序号
	bool operator < (const P &that) const{
		return dis>that.dis;//注意：优先队列要反着写
	}
};
priority_queue<P> q;

松弛

bool vis[maxn];
int n;
int s;
int dijkstra(){
    for(int i=0;i<=n;i++)dis[i]=inf；
    dis[s]=0;
    q.push((P){0,s});//注意:这里第一个位对应dis，第二个位对应id
    while(!q.empty()){
        int u=q.top().id;
        q.pop();
        if(vis[u])continue;
        vis[u]=1;
        for(int i=head[u];i;i=bian[i].next){
            int v=bian[i].to;
            if(dis[v]>dis[u]+bian[i].length){
                dis[v]=dis[u]+bian[i].length;
                q.push((P){dis[v],v});
            }
        }
	}
}

缺点：无法解决负边

SPFA

与dijkstra不同，不用优先选择当前dis最小的出点

queue<int> q;
void spfa(){
    for(int i=1;i<=n;i++)dis[i]=inf;
    dis[s]=0;
    vis[s]=1;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        vis[u]=0;//标记出队
        for(int i=head[u];i;i=bian[i].next){
            int v=bian[i].to;
            if(dis[v]>dis[u]+bian[i].len){
                dis[v]=dis[u]+bian[i].len;
                if(!vis[v]){
                    q.push(v);
                    vis[v]=1;
                }
		   }
        }
    }
}

确保了每条边都跑一遍，可能有一个点多次入列

时间复杂度最高达O(nm)