SDF相关记录
一、生成
1.1 2D SDF: 8ssedt
源: http://www.codersnotes.com/notes/signed-distance-fields/
当然也可以直接暴力算

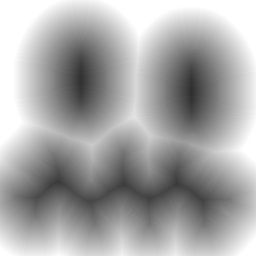
动归算法
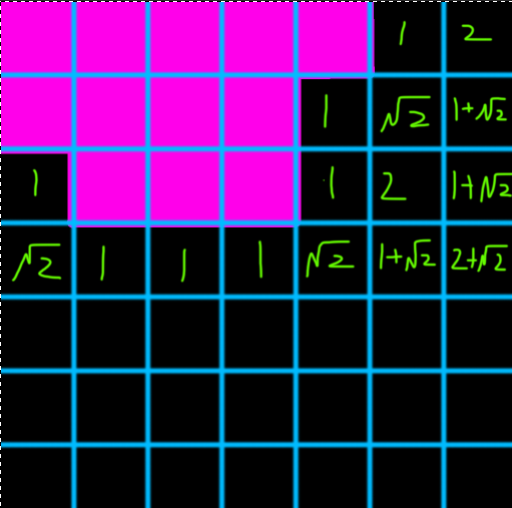
粉色为物体内,黑色为物体外。
- 第一步,标识像素在物体内还是物体外
- 第二步,生成物体外像素的SDF,对应
GenerateSDF- 从上到下、从左到右遍历,对于每个像素相邻 ←↖↑↗四个像素的SDF推算当前像素的SDF,当前行遍历完成之后,从右到左通过比对相邻→的SDF更新当前像素的最近距离(例:如果像素A的↑为物体内,那么A为1,如果像素A的↖为物体内,那么A为\(\sqrt 2\))
- 从下到上、从右到左遍历,对于每个像素相邻↖↑↗→四个像素的SDF推算当前像素的SDF,当前行遍历完成之后,从左到右通过比对相邻←的SDF更新当前像素的最近距离
- 第三步,生成物体内像素的SDF,也是调用
GenerateSDF不过产生的距离是负值,其他和第二步相同
void GenerateSDF( Grid &g )
{
// Pass 0
for (int y=0;y<HEIGHT;y++)
{
for (int x=0;x<WIDTH;x++)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, -1, 0 );
Compare( g, p, x, y, 0, -1 );
Compare( g, p, x, y, -1, -1 );
Compare( g, p, x, y, 1, -1 );
Put( g, x, y, p );
}
for (int x=WIDTH-1;x>=0;x--)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, 1, 0 );
Put( g, x, y, p );
}
}
// Pass 1
for (int y=HEIGHT-1;y>=0;y--)
{
for (int x=WIDTH-1;x>=0;x--)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, 1, 0 );
Compare( g, p, x, y, 0, 1 );
Compare( g, p, x, y, -1, 1 );
Compare( g, p, x, y, 1, 1 );
Put( g, x, y, p );
}
for (int x=0;x<WIDTH;x++)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, -1, 0 );
Put( g, x, y, p );
}
}
}
1.2 3D SDF: K-D Tree、包围盒、射线求交
源:具体代码可以看Unreal的,主要是用空间树加速求交,没有找到类似2D 8ssedt那种加速方法
1.2.1 K-D Tree
关于K-D Tree,这几篇文章讲的不错(下面几张图片来自于链接)
https://baike.baidu.com/item/kd-tree/2302515?fr=aladdin
https://blog.csdn.net/bugrunner/article/details/8962535
https://chengkehan.github.io/kDopTreeInUE4.html
https://zhuanlan.zhihu.com/p/89701518
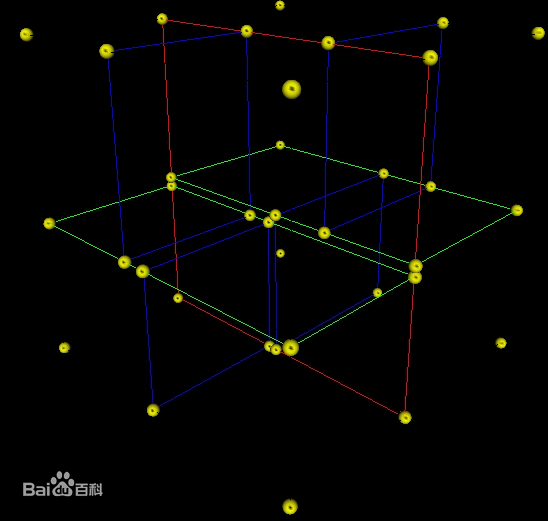
kd树就是xyz三个轴,每次取一个轴,用某个策略找一个最佳的划分点,在这个划分点分割,如此往复,直到把所有三角形都划分到叶子节点里(此外还有不止三根轴的高维度kdop树,以及高维度的kdop包围盒)。
有很多种方法可以选择轴垂直分割面( axis-aligned splitting planes ),所以有很多种创建k-d树的方法。 最典型的方法如下:
1.随着树的深度轮流选择轴当作分割面。(例如:在三维空间中根节点是 x 轴垂直分割面,其子节点皆为 y 轴垂直分割面,其孙节点皆为 z 轴垂直分割面,其曾孙节点则皆为 x 轴垂直分割面,依此类推。)
2.点由垂直分割面之轴座标的中位数区分并放入子树
这个方法产生一个平衡的k-d树。每个叶节点的高度都十分接近。然而,平衡的树不一定对每个应用都是最佳的。
在存储结构上,是一棵二叉树:
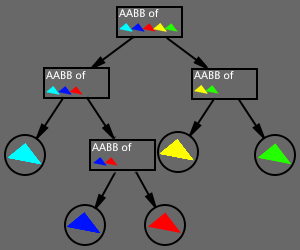
第一个挑选的轴:
首先计算所有三角形的几何中心(模型原点)的平均数,得到的值就可以近似认为是世界的中心,然后计算所有三角形偏离几何中心的方差,方差越大说明三角形更越偏离几何中心。因为几何中心是个三维值,所以方差也是三维的,分别对应 x轴、y轴、z轴,挑选最大方差对应的轴来进行二叉树的构建。
划分点选择策略:
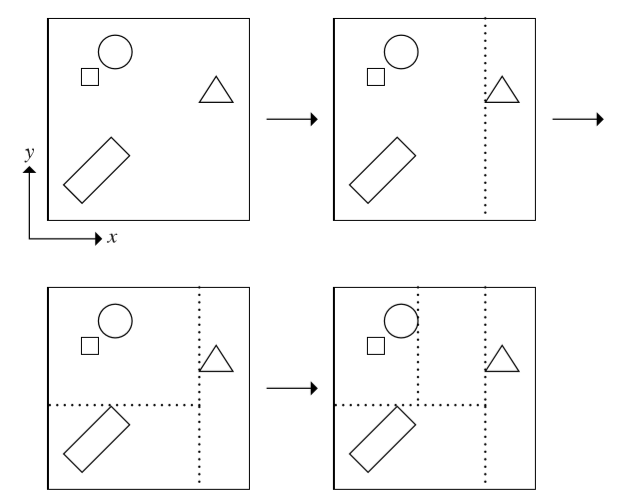
Surface Area Heuristic(SAH)策略找最佳划分点,SAH简单的来说就是认为光线交到一个AABB的概率和这个AABB的表面积成比例,根据SAH,我们先将一个节点里的每个三角形的AABB投影到这个轴上,按顺序排列好:
然后我们认为一个AABB被光线hit到的概率和它的表面积成正比,因此我们要选表面积划分最均匀的点,划分的目标函数是
对所有可能的划分点根据公式计算,取最优进行划分。
过程如下图:
1.2.2 建场
暴力建场的方法,就是直接迭代 n^3 个点,然后在每个点上向周围发射一大堆光线,求交,然后保存交到的最小距离,作为距离场在这个点上的值
值得一提的几个细节是,一般距离场的范围是比物体的AABB大一圈
然后,在物体内部的点,距离存的是负值,然而不是所有曲面都是闭合的,有的时候我们没法区分内和外,虚幻用的是一个heuristic,如果50%以上的光线和三角形的正面相交,那么我们认为这个点在物体外面,如果50%以上的光线与三角形的背面相交,我们认为这个点在曲面内部
二、应用
对于位图信息,每个像素点中存放的是RGB颜色,是标量,通过插值运算得到的结果无实际意义。但对于SDF,每个点存放的是到边界的有向距离,是一个向量,向量通过插值运算得到的结果就是某种意义上的实际值
位图存的是每个像素点颜色,颜色是一个标量。两个颜色相加再平均是没有意义的,只是数学上面的混合,对于图像还原来说,就是错误的。SDF每个像素点存的是一个有方向的矢量,最终变成我们看见的图片是需要通过一个计算才能还原的,所以直接对SDF图的像素点操作,实质上是操作向量,放大过程实质上就是向量重建的过程,是不损失精度的。SDF就是利用了插值器的特性实现了光滑放大效果。
2.1 2D SDF
2.1.1 防止UI、字体失真

2.1.2 平滑过渡图像
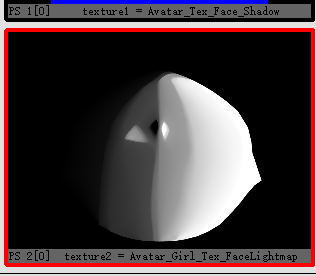

这种图的生成步骤:
1画多种阴影分布情况,当然要求图层有梯度差异,类似这样
2分别生成SDF
3混合这几张SDF图
运行时采样最后生成的图,以dot(LightDir, N') * 0.5f + 0.5f做阈值之类的,其中N'是面朝向
2.2 3D SDF
2.2.1 加速Ray Marching
下面用的图来自于链接
https://zhuanlan.zhihu.com/p/89701518
https://zhuanlan.zhihu.com/p/262332553
https://zhuanlan.zhihu.com/p/92017307
因为可以确定当前位置在半径x范围内不会有交点,所以可以直接迈x的距离。
- 动态环境光源遮蔽 DFAO
- 距离场阴影,不会增加DC,有近距离用Shadow Map远距离距离场阴影的方案。
- GI
- 体渲染加速(云、水、雾等)
以后处理的方式,对于距离场阴影来说:
做法大致是,先光源空间分tile和每个mesh的bound求交,存tile list,然后每个像素在trace的时候变换到光源空间,从tile list里取可能相交的mesh sdf贴图,然后对这些贴图进行march。虚幻的sdf阴影是没有合并mesh sdf到global sdf的,只是将所有的mesh sdf给atlas到一张512^3的体贴图上(300m显存)。
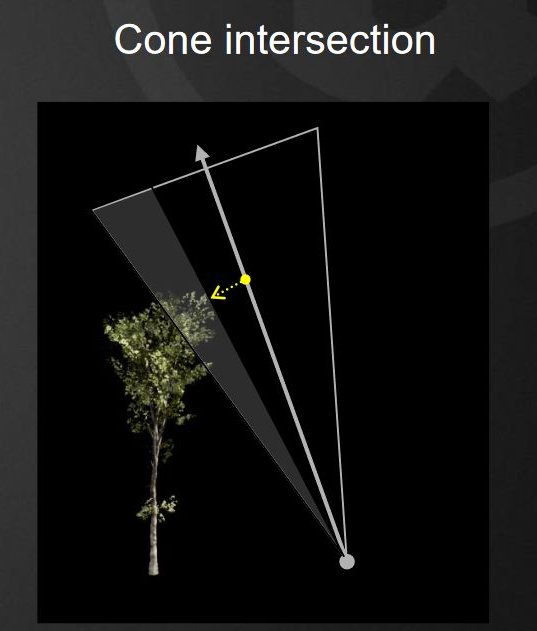
我们选定一个cone的角度,这个cone的角度越大,阴影越软,选定好后,沿着cone的中心轴步进,采样到的距离场值,就是其位置到最近点的距离,我们要找的是这跟中心轴上被遮蔽得最厉害的点,也就是(距离/圆锥半径)的最小值:
float dist = gSdfTextures[sdfInd].Sample(basicSampler, pos).r;
shadow = min(shadow, saturate(dist / (totalDis * CONE_TANGENT)));
遇到负数,说明是本影,就可以early out
链接中也提到了距离场阴影的弊端,不支持顶点动作,最多对物体Transform,因为可以对Mesh SDF也Transform。
如果要给人用,可以用一些胶囊来堆,然后Transform胶囊的SDF
https://docs.unrealengine.com/4.26/zh-CN/BuildingWorlds/LightingAndShadows/CapsuleShadows/Overview/

AO是根据世界空间剔除,而阴影是根据光源剔除;而且不止是给光源方向Cone,而是所有方向:
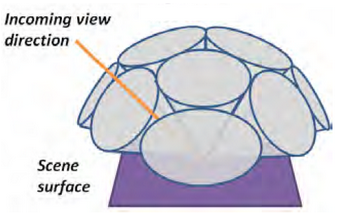
2.2.2 各种其他Shader效果
液体材质:
https://zhuanlan.zhihu.com/p/73754807

水中物体对水流向的影响
物体Blend:
https://zhuanlan.zhihu.com/p/41801203

未完待续



 浙公网安备 33010602011771号
浙公网安备 33010602011771号