GAMES202笔记：IBL原理详解

Image-Based Lighting

环境贴图就是在场景中任意一点往四周看去可看到的光照，将其记录在一张图上这就是环境光照，或者也可以叫做IBL(image-based lighing)。通常我们用spherical map或cube map来存储环境光照。

下面将解释IBL的原理与UE4中的实现方法。

1. 渲染方程

还是从渲染方程开始说起：

\[L_{o}\left(p, \omega_{o}\right)=L_{e}\left(p, \omega_{o}\right)+\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)V(p,\omega_{i}) \mathrm{d} \omega_{i} \]

IBL不考虑遮挡，所以Visibility项可以舍去：

\[L_{o}\left(p, \omega_{o}\right)=L_{e}\left(p, \omega_{o}\right)+\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)\mathrm{d} \omega_{i} \]

渲染方程相关记录中使用了蒙特卡洛方法将积分分解成采样大量随机样本可以得到一个近似解：

\[\begin{aligned} L_{o}\left(p, \omega_{o}\right) &=L_{e}\left(p, \omega_{o}\right)+\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i} \\ & \approx L_{e}\left(p, \omega_{o}\right)+\frac{1}{N} \sum_{i=1}^{N} \frac{L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)}{p\left(\omega_{i}\right)} \end{aligned} \]

但实时对每个着色点做一遍蒙特卡洛开销无法接受。

2. 近似公式

2.1 近似公式

实时渲染中，经常用到一个约等式：

\[ \int_\Omega{f(x)g(x)}\mathrm{d}x\approx\frac{\int_{\Omega_G}{f(x)\mathrm{d}x}}{\int_{\Omega_G}\mathrm{d}x}\cdot\int_\Omega{g(x)\mathrm{d}x} \]

需要注意，\(f(x)\)积分范围从\(\Omega\)变成了\(\Omega_G\)，只需要积有值的范围即可。
这个约等式成立有两个条件，满足两个条件之一，渲染领域就认为他们相似相等：

• \(g(x)\)的积分域很小
• \(g(x)\)足够smooth

2.2 相关案例

以渲染方程中的Visibilty项为例（为了方便不考虑自发光）：

\[L_{o}\left(p, \omega_{o}\right)=\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)V(p,\omega_{i}) \mathrm{d} \omega_{i} \]

使用约等式把渲染方程的\(V\)项拿到积分外：

\[L_{o}\left(p, \omega_{o}\right)\approx\frac{\int_{\Omega^+}{V(p,\omega_{i})\mathrm{d} \omega_{i}}}{\int_{\Omega^+}\mathrm{d} \omega_{i}} \cdot\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i} \]

此约等式成立的条件：

• \(g(x)\)的积分域很小：点光源（一个位置）或方向光源（一个方向）
• \(g(x)\)足够smooth：Diffuse的BRDF 且 面光源的Radiance是均匀分布的

这也是Shadow Map的一个解释。

3. 使用近似公式拆分L项和BRDF项

首先BRDF有两种情况：

• brdf为glossy时，覆盖在球面上的范围很小，也就是small support(积分域)
• brdf为diffuse时，它会覆盖整个半球的区域，但是是smooth的，也就是值的变化不大，就算加上cos也是相对平滑的

满足近似公式成立条件，可以得到不考虑遮挡项的渲染方程的近似：

\[L_{o}\left(p, \omega_{o}\right)\approx\frac{\int_{\Omega_{f_r}}{ L_{i}\left(p, \omega_{i}\right) \mathrm{d} \omega_{i}}}{\int_{\Omega_{f_r}}\mathrm{d} \omega_{i}} \cdot\int_{\Omega^{+}}f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i} \]

4. 处理L项的积分

L项的积分范围，是和BRDF范围相关的：

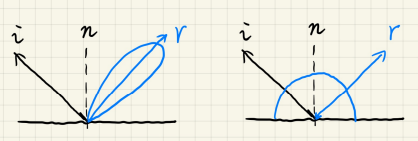
为了只采样一次入射光，需要对环境贴图进行模糊。不同的BRDF有不同的滤波核大小。

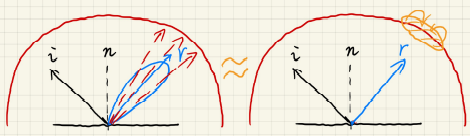
L值在BRDF相邻两个Level采样结果之间差值：

这样对于一个着色点，L的值只需要两次采样并差值就可以得到。

5. 处理BRDF项的积分

仍然可以用预计算来解决后半部分积分采样的问题，但是预计算的话我们需要将参数的所有可能性均考虑进去，维度太高，存储空间太大，需要降低维度。
假设我们使用Microfacet BRDF模型：

\[f(p,\omega_i,\omega_o) = \frac{F(o,h)G(i,o,n)D(h)}{4(n,i)(n,o)} \]

• F是菲涅尔项，主要参数有三通道的初始反射率\(R_0\)，以及观察方向\(\omega_o\)
• G是几何项，主要表示微表面之间的遮挡关系，主要参数有法线\(n\)，观察方向 \(\omega_o\)
• D是法线分布函数（NDF），主要参数有观察方向 \(\omega_o\)，粗糙度\(\alpha\)等（半程向量\(h\)可以借由 \(\omega_o\) \(\omega_i\)计算得到）

microfacet brdf中，考虑的是菲涅尔项、遮挡项以及法线分布项，由于此时暂时不考虑阴影，此处需要关注的是F和D。其中\(R_0\)，\(\omega_o\)，\(n\)均为三维向量，再加上\(\alpha\)，存储容量爆炸。

5.1 菲涅尔项：将\(R_0\)拆除积分

首先，我们使用菲涅尔项的Schlick's approximation来替代BRDF中的\(F(o,h)\)，Schlick's approximation可以表示为：

\[R(\theta) = R_0+(1-R_0)(1-(h\cdot\omega_o))^5\\ R_0=(\frac{n_1-n_2}{n_1+n_2}) \]

其中\(\omega_o\)是观察方向，\(n_1\)、\(n_2\)是两种介质的折射率
带入BRDF：

\[\begin{aligned} \int_{\Omega^+}f_r(p,\omega_i,\omega_o)cos\theta_i \mathrm{d}\omega_i&=\int_{\Omega^+}\frac{f_r(p,\omega_i,\omega_o) }{F(o,h)}F(o,h)cos\theta_i\mathrm{d}\omega_i \\ &=\int_{\Omega^+}\frac{f_r(p,\omega_i,\omega_o) }{F(o,h)}(R_0+(1-R_0)(1-(h\cdot\omega_o))^5)cos\theta_i\mathrm{d}\omega_i\\ &=R_0\int_{\Omega^+}\frac{f_r(p,\omega_i,\omega_o) }{F(o,h)}(1-(1-(h\cdot\omega_o))^5)cos\theta_i\mathrm{d}\omega_i+\int_{\Omega^+}\frac{f_r(p,\omega_i,\omega_o) }{F(o,h)}(1-(h\cdot\omega_o))^5cos\theta_i\mathrm{d}\omega_i \end{aligned} \]

我们按顺序做了如下的变形：
1、在BRDF项中显式考虑菲涅尔项，并做了一个恒等
2、变形用Schlick's approximation替换其中一个菲涅尔项
3、将替换后的积分式拆开，将\(R_0\) 单独提取出来

5.2 法线分布项：使用夹角\(\theta\)代替\(\omega_o\)、\(n\)

假设此处的BRDF我们使用各项同性的法线分布函数，比如Beckmann分布：

\[D(h)=\frac{e^{-\frac{tan^2\theta{h}}{\alpha^2}}}{\Pi\alpha^2cos^4\theta_h}(cos\theta_h=(h\cdot{n})) \]

将半程向量\(h\)拆开可得：

\[h\cdot{n}=(\frac{\omega_o+\omega_i}{2})\cdot{n}=\frac{\omega_o\cdot{n}+\omega_i\cdot{n}}{2}=\frac{cos\theta_o+cos\theta_i}{2} \]

菲涅尔项中的\(h\cdot{\omega_o}\)也可以拆开：

\[h\cdot{\omega_o}=(\frac{\omega_o+\omega_i}{2})\cdot{\omega_o}=\frac{\omega_o\cdot{\omega_o}+\omega_i\cdot{\omega_o}}{2}=\frac{1+cos(\theta_o+\theta_i)}{2} \]

其中带\(i\)下标的是积分变量。可以看出其实我们并不太关注 \(\omega_o\)和\(n\)的具体值，我们只关心它们的夹角\(\theta_o\)。也就是说，不论\(\omega_o\)的方向如何变化，只要夹角\(\theta_o\)不变，积分A和B的值就不会发生变化。

5.3 预计算的二维纹理

经过上述的近似拆分过程，我们将原BRDF积分项拆成了两个积分并将积分所依赖的参数降到了2个，\(\theta_o\)和粗糙度 \(\alpha\)。可以选取不同的\(\theta_o\)和粗糙度\(\alpha\)，分别计算两个积分，保存到一张2D纹理的两个通道：

当使用时输入\(\theta_o\)和 \(\alpha\) ，在纹理上查询出两个积分的值，再结合初始反射率 \(R_0\) ，就可以计算出原BRDF的积分结果。

6. 总结

首先不考虑遮挡把\(V\)项干掉；用近似公式将\(L\)和\(BRDF\)拆开；通过对Cube Map生成Mipmap采样差值取\(L\)；将BRDF预计算为一张二维纹理，运行时采样成反射率可得到。

本文结束

引用

GAMES202
图片来自GAMES202课件
https://zhuanlan.zhihu.com/p/371112302
https://zhuanlan.zhihu.com/p/370207345