应力比值的地球物理含义

应力比值的地球物理含义

​ 应力比值（Stress Ratio，通常表示为\(R=\frac{\sigma_{2}-\sigma_{3}}{\sigma_{1}-\sigma_{3}}\)）是描述构造应力场特征的重要参数，它反映了三个主应力之间的相对大小关系，具有明确的地球物理意义，对页岩气的开发具有总要的指导意义。在本笔记中将详细解释其具体含义以及地质解释。

1.应力比值的定义

区域应力张量可表示为

\[\mathbf{\boldsymbol{\tau}}=\left(\begin{array}{111} \tau_{xx}&\tau_{xy}&\tau_{xz}\\ \tau_{xy}&\tau_{yy}&\tau_{yz} \\ \tau_{xz}&\tau_{yz}&\tau_{zz} \end{array}\right) \tag{1} \]

在实际中应力张量\(\mathbf{\boldsymbol{\tau}}\) 分解为偏应力张量(Deviatoric Stress)和各向同性应力部分：

\[ \mathbf{\boldsymbol{\tau}}=\boldsymbol{\sigma}+p\mathbf{I} \tag{2} \]

其中\(p=\frac{1}{3}(\tau_{xx}+\tau_{yy}+\tau_{zz})\) 为平均应力，\(\mathbf{\boldsymbol{\sigma}}\) 为偏应力张量（无迹张量）。在基于震源机制的应力反演,其主要结果为偏应力张量\(\sigma\)，根据应力张量进行特征值分解得到无剪切分量的主应力表达：

\[\boldsymbol{\sigma}=\sigma_1\mathbf{v_1}\mathbf{v_1}^T+\sigma_2\mathbf{v_2}\mathbf{v_2}^T+\sigma_3\mathbf{v_3}\mathbf{v_3}^T \tag{3} \]

其中 \(\sigma_1,\sigma_2,\sigma_3\)为偏应力张量的主应力 ，\(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\) 为 主应力对应方向向量如图1表达。

​

图1 基于 Aderson断层模型主应力状态

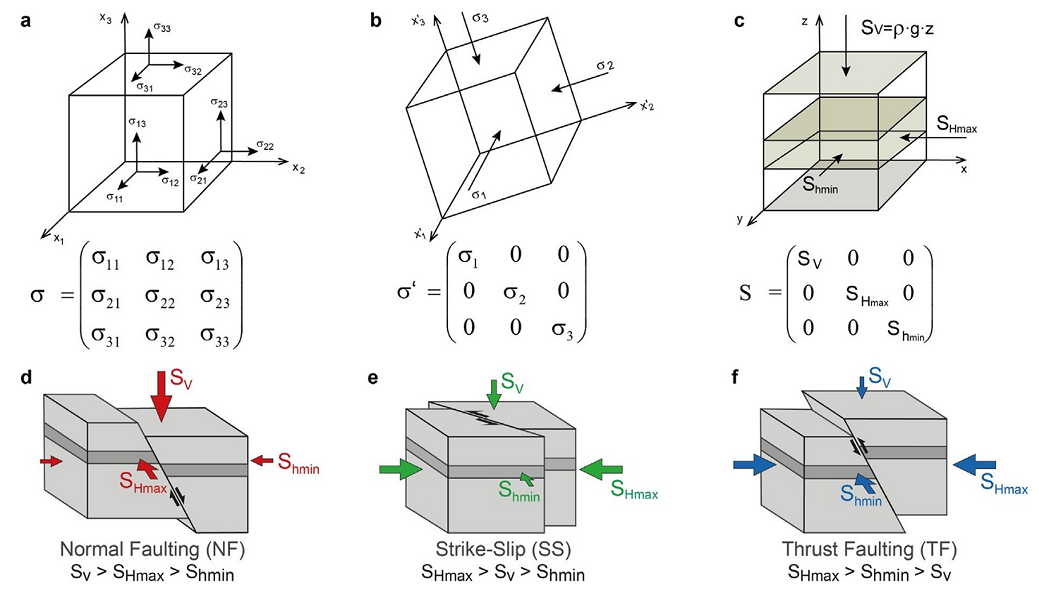
应力比值R的定义基于偏应力张量的主应力大小(\(\sigma_1\geq\sigma_2\geq\sigma_3\))：

\[\mathbf{R}=\frac{\sigma_2-\sigma_3}{\sigma_1-\sigma_3} \tag{4} \]

其中，\(\sigma_1\)为最大主应力(压应力为正)，\(\sigma_3\)为最小主应力，\(\sigma_2\)为中间大小主应力。由于分母\(\sigma_1-\sigma_3\) 是主应力差异（应力偏量的大小），\(R\)的取值范围为\(0\leq{R}\leq{1}\)

2.地球物理意义

应力比值\(R\) 的关键意义在于量化中间主应力的作用，进而揭示区域应力场的类型和地壳变形机制：

（1）反映应力状态的类型

• 当\(R=0\)时：\(\sigma_2=\sigma_3\), 表示应力状态为单轴压缩(Uniaxial Compression)，即中间主应力与最小主应力相等。这种状态常见于强烈挤压环境（如俯冲带或逆冲断层）。

• 当\(R=1\)时：\(\sigma_2=\sigma_1\), 表示应力状态为单轴拉伸(Uniaxial Extension)，即中间主应力与最大主应力相等。这种状态多出现在伸展环境（如裂谷或正断层区）。

• 当\(0<R<1\)时：中间主应力\(\sigma_2\) 介于\(\sigma_1\)和\(\sigma_3\) ，对应三轴应力状态(Triaxial Stress) , 这是地壳中最常见的情况。

  \(R<0.5\): 中间应力更接近最小主应力，应力状态偏向于压缩(Compression)。

  \(R>0.5\): 中间应力更接近最大主应力，应力状态偏向于拉伸(Extension)。

（2）与断层类型

应力比值\(R\) 与断层类型密切相关（见图1)：

• 逆断层(Thrust Fault): 通常对应\(R<0.5\)，最大主应力（\(\sigma_1\)）垂直，最小主应力（\(\sigma_3\)）水平，中间应力（\(\sigma_2\)）作用较弱。
• 正断层(Normal Fault): 通常对应\(R>0.5\), 最小主应力 (\(\sigma_3\)) 垂直，最大主应力 (\(\sigma_1\)) 水平，三主应力大小比较接近。
• 走滑断层(Strike-Slip Fault): 通常对应\(R\approx0.5\)，最大和最小主应力均为水平方向，中间主应力垂直。

（3）揭示地壳变形机制

• 低\(R\)值(接近于0)：表明中间主应力对断层滑动的影响较小，地壳变形主要由最大和最小主应力主导，对应强烈挤压或拉张环境；
• 高\(R\)值(接近于1)：表明中间主应力接近于最大主应力，地壳可能存在于多向伸展或复杂剪切状态；
• \(R\approx0.5\) :中间主应力更加接近于最大主应力，中间应力在变形中起着平衡作用。

3.实际应用方向

（1）应力反演中的约束条件

在震源机制应力反演中、\(R\)是重要的待求参数。通过反演多个震源机制解，可以确定区域的\(R\)值，进而推断：

• 主应力方向的相对稳定性；
• 区域构造活动的类型（挤压、伸展或走滑）

（2）板块边界与构造环境

• 俯冲带：通常\(R\)较低 （挤压主导）, 如日本海沟 \(R\approx0.2-0.4\)
• 裂谷带：通常\(R\)较高 （拉伸主导)，如东非裂谷 \(R\approx0.6-0.8\)
• 转换断层：如圣安德烈断层，\(R\approx0.4-0.6\) ,反映走滑与局部挤压、伸展的叠加

（3）地震危险

\(R\)值可帮助评估断层的潜在活动性：

• 低\(\mathbf{R}\) 值区域可能更容易可能更容易发生逆断层型大地震(如喜马拉雅前沿)；
• 高\(\mathbf{R}\) 值区域可能以正断层活动为主(如盆地与山脉省)

4.应力比值\(R\)的局限性

• 模型假设简化：应力比值基于偏应力张量的各向同性部分（双力偶模型）没有考虑裂缝断裂张离情况。
• 非唯一性（多解性）：相同的\(\mathbf{R}\) 值可能对应不同的构造环境，需要结合地质背景综合解释。

总 结

​ 应力比值 \(R\) 是连接震源机制解与区域构造应力场的关键参数，其值的大小揭示了中间主应力的作用强度、地壳变形的主导机制以及断层的活动类型。通过反演 \(R\) 值，地球物理学家可以定量分析构造应力场的特征，为地震机理研究和灾害预测提供重要依据。