MKL库求解矩阵特征值、特征向量(LAPACKE_dgeev、dsyev)
LAPACK(Linear Algebra PACKage)库,是用Fortran语言编写的线性代数计算库,包含线性方程组求解(\(AX=B\))、矩阵分解、矩阵求逆、求矩阵特征值、奇异值等。该库用BLAS库做底层运算。
本示例将重点介绍使用LAPACK库求解非对称矩阵与对称矩阵的特征值、特征向量过程。
1 一般矩阵
在LAPACK库中,使用?geev函数计算一般矩阵的特征值及其左/右特征向量,其中右特征向量\(v_j\)满足
\[A*v_j = \lambda_j*v_j
\]
左特征向量\(u_j\)满足
\[u_j^H*A = \lambda_j*u_j^H
\]
其中\(u_j^H\)表示\(u_j\)的共轭转置。
1.1 参数详解
示例将使用MKL库中,LAPACK中的dgeev函数演示。
lapack_int LAPACKE_dgeev( matrix_order, //(input) 行优先(LAPACK_ROW_MAJOR)或列优先(LAPACK_COL_MAJOR)
jobvl, //(input) 指定是否计算左特征向量,"V":计算;"N":不计算
jobvr, //(input) 指定是否计算右特征向量,同上
n, //(input) 矩阵的阶数
a, //(input/output) 待求解A矩阵
lda, //(input) A矩阵的第一维
wr, //(output) 特征向量实部
wi, //(output) 特征向量虚部
vl, //(output) 左特征向量
ldvl, //(input) 左特征向量第一维
vr, //(output) 右特征向量
ldvr //(input) 右特征向量第一维
)
1.2 定义待求解矩阵
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
// 参数
#define N 5
#define LDA N
#define LDVL N
#define LDVR N
MKL_INT n = N, lda = LDA, ldvl = LDVL, ldvr = LDVR, info;
double wr[N], wi[N], vl[LDVL*N], vr[LDVR*N];
double a[LDA*N] = {
-1.01, 0.86, -4.60, 3.31, -4.81,
3.98, 0.53, -7.04, 5.29, 3.55,
3.30, 8.26, -3.89, 8.20, -1.51,
4.43, 4.96, -7.66, -7.33, 6.18,
7.31, -6.43, -6.16, 2.47, 5.58
};
1.3 求解特征值、特征向量
LAPACKE_dgeev( LAPACK_ROW_MAJOR, 'V', 'V', n, a, lda, wr, wi, vl, ldvl, vr, ldvr );
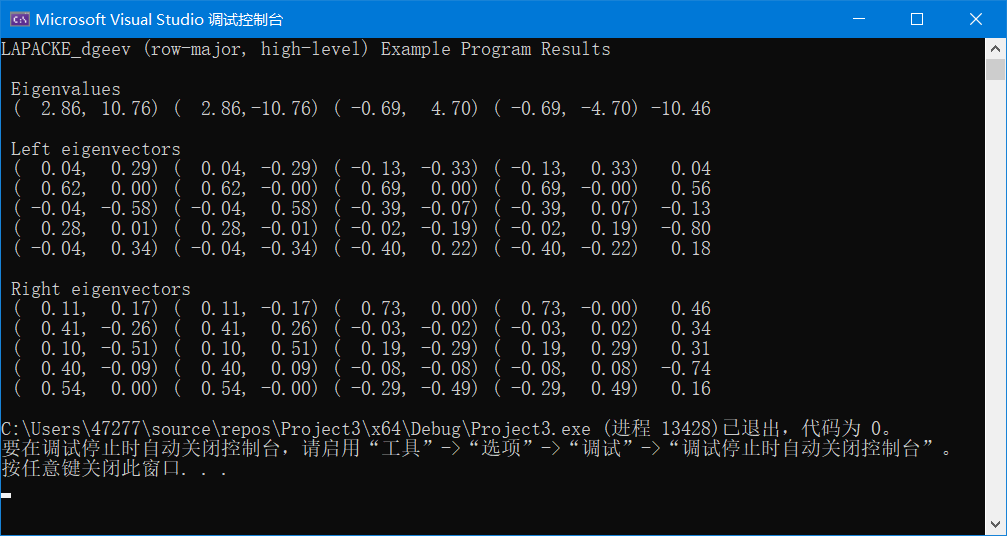
与Matlab中使用eig方法求取特征值与特征向量,所得结果相同。
A = [ -1.01, 0.86, -4.60, 3.31, -4.81;
3.98, 0.53, -7.04, 5.29, 3.55;
3.30, 8.26, -3.89, 8.20, -1.51;
4.43, 4.96, -7.66, -7.33, 6.18;
7.31, -6.43, -6.16, 2.47, 5.58];
[V,D]=eig(A);
Vector = V;
Lambda = diag(D);
display(Lambda);
display(Vector);
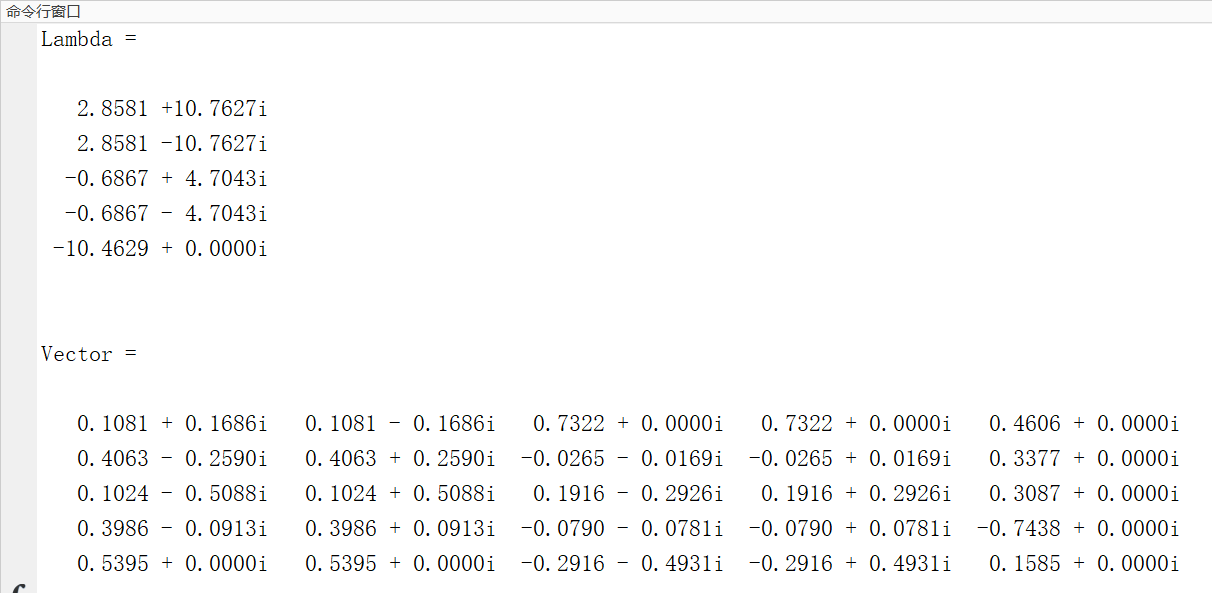
完整代码
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
//print特征值和特征向量
extern void print_eigenvalues( char* desc, MKL_INT n, double* wr, double* wi );
extern void print_eigenvectors( char* desc, MKL_INT n, double* wi, double* v,
MKL_INT ldv );
#define N 5
#define LDA N
#define LDVL N
#define LDVR N
int main() {
MKL_INT n = N, lda = LDA, ldvl = LDVL, ldvr = LDVR, info;
double wr[N], wi[N], vl[LDVL*N], vr[LDVR*N];
double a[LDA*N] = {
-1.01, 0.86, -4.60, 3.31, -4.81,
3.98, 0.53, -7.04, 5.29, 3.55,
3.30, 8.26, -3.89, 8.20, -1.51,
4.43, 4.96, -7.66, -7.33, 6.18,
7.31, -6.43, -6.16, 2.47, 5.58
};
printf( "LAPACKE_dgeev (row-major, high-level) Example Program Results\n" );
// 求解
info = LAPACKE_dgeev( LAPACK_ROW_MAJOR, 'V', 'V', n, a, lda, wr, wi,
vl, ldvl, vr, ldvr );
if( info > 0 ) {
printf( "The algorithm failed to compute eigenvalues.\n" );
exit( 1 );
}
print_eigenvalues( "Eigenvalues", n, wr, wi );
print_eigenvectors( "Left eigenvectors", n, wi, vl, ldvl );
print_eigenvectors( "Right eigenvectors", n, wi, vr, ldvr );
exit( 0 );
}
void print_eigenvalues( char* desc, MKL_INT n, double* wr, double* wi ) {
MKL_INT j;
printf( "\n %s\n", desc );
for( j = 0; j < n; j++ ) {
if( wi[j] == (double)0.0 ) {
printf( " %6.2f", wr[j] );
} else {
printf( " (%6.2f,%6.2f)", wr[j], wi[j] );
}
}
printf( "\n" );
}
void print_eigenvectors( char* desc, MKL_INT n, double* wi, double* v, MKL_INT ldv ) {
MKL_INT i, j;
printf( "\n %s\n", desc );
for( i = 0; i < n; i++ ) {
j = 0;
while( j < n ) {
if( wi[j] == (double)0.0 ) {
printf( " %6.2f", v[i*ldv+j] );
j++;
} else {
printf( " (%6.2f,%6.2f)", v[i*ldv+j], v[i*ldv+(j+1)] );
printf( " (%6.2f,%6.2f)", v[i*ldv+j], -v[i*ldv+(j+1)] );
j += 2;
}
}
printf( "\n" );
}
}
2 求解对称阵
2.1 参数详解
采用LAPACKE_dsyev方法实现,参数比LAPACKE_dgeev少,含义相似。
lapack_int LAPACKE_dsyev( matrix_layout,
jobz, //是否计算特征值和特征向量, "V"/"N"
uplo, //表示使用A矩阵的上三角或下三角矩阵 "U"/"L"
n,
a,
lda,
w //包含降序的特征值
)
完整代码
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
extern void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda);
#define N 5
#define LDA N
int main() {
MKL_INT n = N, lda = LDA, info;
double w[N];
double a[LDA * N] = {
1.96, - 6.49, - 0.47, - 7.20, - 0.65,
-6.49, 3.80, - 6.39, 1.50, - 6.34,
-0.47, - 6.39, 4.17, - 1.51, 2.67,
-7.20, 1.50, - 1.51, 5.70, 1.80,
-0.65, - 6.34, 2.67, 1.80, - 7.10,
};
printf("LAPACKE_dsyev (row-major, high-level) Example Program Results\n");
//求解特征值、特征向量
info = LAPACKE_dsyev(LAPACK_ROW_MAJOR, 'V', 'U', n, a, lda, w); //'U'表示下三角
if (info > 0) {
printf("The algorithm failed to compute eigenvalues.\n");
exit(1);
}
print_matrix("Eigenvalues", 1, n, w, 1);
print_matrix("Eigenvectors (stored columnwise)", n, n, a, lda);
exit(0);
}
void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda) {
MKL_INT i, j;
printf("\n %s\n", desc);
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) printf(" %6.2f", a[i * lda + j]);
printf("\n");
}
}
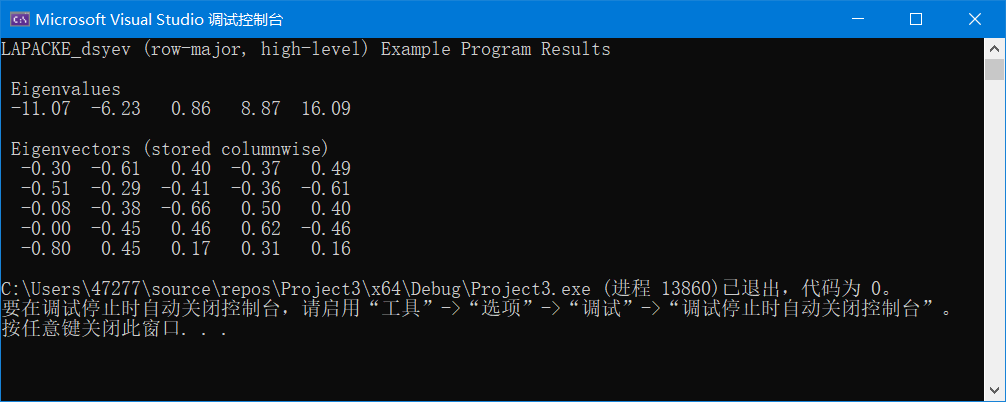
输出为:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号