[算法模版]树形背包
[算法模版]树形背包
树形01背包
树形01背包和普通背包不同点在于物品之间有相互的依赖关系。选取儿子物品的必要条件是选取了所有他的祖先。
我们考虑使用dp[i][j]代表第i个点的子树内,花费了j个容量能得到的最大权值。
伪代码:
for(int i=1;i<=son;i++){//枚举所有儿子
dfs(son[i]);//先处理儿子
for(int j1=m;j1>=0;j1--){//枚举当前点用掉了多少容量(正着枚举会变成完全背包)
for(int j2=0;j2<=j1;j2++){//枚举这个儿子分配多少
dp[i][j1]=max(dp[i][j1],dp[i][j1-j2]+dp[son[i]][j2]);//更新状态
}
}
}
显然,复杂度是\(O(n*m^2)\)的。
特殊情况的树形背包优化
当物品的体积全部为1时,我们可以把它优化到\(O(n^2)\)的复杂度。
来自lsj爷爷的代码:
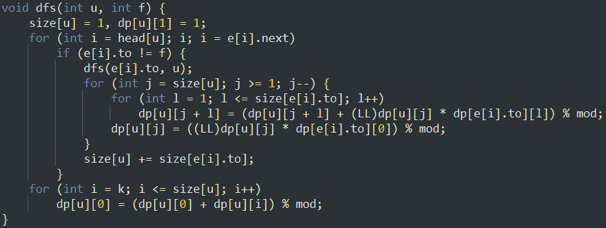
乍一看根原来的没什么不同,但是需要注意,对于每一对点,都只会在他们的LCA被枚举到一次。可以自己想想为什么。
复杂度\(n^2\)。
树形01背包优化
有一种方法可以把它优化到\(n*m\)的复杂度。
在这种dp方法中,dp[i][j]是指在点i及其所有祖先必须选,dfs序小于i和i子树内的可以选,对于容量为j的背包,最大权值是多少。
所以代码也很简单:
void dfs(int now,int fa){
for(int i=w[now];i<=m;i++){
dp[now][i]=dp[fa][i-w[now]]+v[now];
}
for(int i=0;i<w[now];i++)dp[now][i]=-1e9;
for(int i=head[now];i;i=side[i].next){
int v=side[i].v;if(v==fa)continue;
dfs(v,now);
for(int j=w[v];j<=m;j++){
dp[now][j]=max(dp[now][j],dp[v][j]);
}
}
}
注意,必须把所有不可行的方案置为-1e9,否则虽然这种方案答案是0,但是它的儿子可能在这种不成立的状态基础上转移出一个答案很大的状态。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号