【bzoj4002】[JLOI2015]有意义的字符串 数论+矩阵乘法
题目描述
B 君有两个好朋友,他们叫宁宁和冉冉。有一天,冉冉遇到了一个有趣的题目:输入 b;d;n,求
.png)
输入
一行三个整数 b;d;n
输出
一行一个数表示模 7528443412579576937 之后的结果。
样例输入
1 5 9
样例输出
76
提示
其中 0<b^2<=d<(b+1)^2<=10^18,n<=10^18,并且 b mod 2=1,d mod 4=1
题解
数论 高中数学
注意题目中给出的0<b^2<=d<(b+1)^2,这说明了什么?
就是在变相的告诉我们b<=√d<b+1,也就是-1<b-√d<=0,即0<=|b-√d|<1。
那么0<=|b-√d|^n<1,可以看出这个数对整数部分的影响是常数级的。
不妨设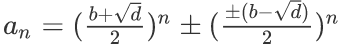
那么an一定恒为整数。
将n=1代入,可知两个±号一定相同,于是只有2种情况
再由通项公式求递推公式,发现只有一种情况符合条件,即:
 ,通项公式为
,通项公式为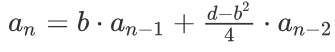
根据题目条件b mod 2=1,d mod 4=1可知前面的系数都为整数,于是可以矩阵乘法来推。
推完之后再讨论后一项的影响即可。
ps: n可能等于0,所以需要特判或者从a0开始推。
ps2: 题目中mod较大,需要用到unsigned long long和快速乘
#include <cstdio>
#include <cstring>
#include <algorithm>
#define mod 7528443412579576937ull
using namespace std;
typedef unsigned long long ull;
ull qmul(ull x , ull y)
{
ull ans = 0;
while(y)
{
if(y & 1) ans = (ans + x) % mod;
x = (x + x) % mod;
y >>= 1;
}
return ans;
}
struct matrix
{
int n , m;
ull num[2][2];
matrix()
{
n = m = 0 , memset(num , 0 , sizeof(num));
}
matrix operator*(matrix a)
{
matrix t;
t.n = n , t.m = a.m;
int i , j , k;
for(i = 0 ; i < t.n ; i ++ )
for(j = 0 ; j < t.m ; j ++ )
for(k = 0 ; k < m ; k ++ )
t.num[i][j] = (t.num[i][j] + qmul(num[i][k] , a.num[k][j])) % mod;
return t;
}
}A , B;
matrix qpow(matrix x , ull y)
{
matrix t;
t.n = x.n , t.m = x.m;
int i;
for(i = 0 ; i < x.n ; i ++ )
t.num[i][i] = 1;
while(y)
{
if(y & 1) t = t * x;
x = x * x;
y >>= 1;
}
return t;
}
int main()
{
ull b , d , n , x , y , ans;
scanf("%llu%llu%llu" , &b , &d , &n);
x = b , y = (d - b * b) / 4;
A.n = 1 , A.m = 2 , A.num[0][0] = 2 , A.num[0][1] = b;
B.n = 2 , B.m = 2 , B.num[0][1] = y , B.num[1][0] = 1 , B.num[1][1] = x;
ans = (A * qpow(B , n)).num[0][0];
if(y && n % 2 == 0) ans = (ans + mod - 1) % mod;
printf("%llu\n" , ans);
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号