深入理解IEEE754浮点格式
今天看到一个浮点运算的问题, 觉得很有代表性, 就记录一下. 有同事问下面这段代码运行结果是什么, 还很贴心的给了4个选项:
A. 30500 (0.000061 * 500 * 1000000)
B. 与A同量级的近似值
C. 具体值不知道, 但肯定是小于A量级某个浮点数
D. 1024.0 (精确值)
#include <stdlib.h>
#include <stdio.h>
#define LOOP 1000000
#define NUM 500
#define DATA 0.000061
int main() {
float *pf = malloc(NUM * sizeof(float));
for (int i = 0; i < NUM; ++i)
pf[i] = DATA;
float res = 0.0;
for (int j = 0; j < LOOP; ++j)
for (int i = 0; i < NUM; ++i)
res += pf[i];
printf("%f\n", res);
return 0;
}
问了周围几个人都回答B或者C, 其中答B居多. 能够答C的已经考虑比较周全了, 但是还是对IEEE754的格式没有明确的理解.
先说下答案是D, 实际上在循环次数足够大的情况下其结果仅与DATA值相关. 为什么? 这与IEEE754的编码与计算方式有关.
浮点数的由来与IEEE754格式
早期的处理器只支持整型运算单元, 每个整型数据一对一唯一的编码成二进制数据(i.e. 5 = 0b101, 11 = 0b1011), 制约数值表达范围的因素仅有一个: 数据编码长度.
当然编码长度与硬件成本息息相关, 不同的变量有不同的取值范围, 所以程序员设计了char, short, int, long等不同位宽的数据类型来支持不同范围的数据运算.
但是当编码扩展到小数时问题就来了: 编码的最低位等于整数1(即整型数据的表示方式的最小间距是1), 那该如何表示一个小于1的间距(值)呢?
基础的想法是像自然数学一样扩展, 以某个位为起始, 其低位的位用来表示小数部分, 离基础位越近的权重越大. i.e. 若取低8位作为小数部分则有
1 = 0x100
1000 = 0x3e800
0.5 = 1 / 2 = 0x100 >> 1 = 0x80
0.125 = 0x20
1000.125 = 0x3e820
这种定点数的编码方式有几个显而易见的问题:
- 表达的精度有限, 误差为2的-n次(n为小数编码位数). 如果想要扩展精度只有小数部分的编码位数.
- 由于小数部分占据的编码低位, 不同精度的定点数不能直接通过加法器相加(高精度的编码的小数部分的MSB是低精度的编码的整数部分的LSB).
- 当编码的数值较大以至于小数部分可以忽略时(i.e. 上文中的1000.125)会造成编码空间的浪费(8bit编码仅表达数值的万分之一).
为解决以上问题程序员将科学计数法引入编码中, 现在一个数值的编码由两部分相乘组成: 以2为底的指数(被称为exponent)与一个小于1的分数(被称为fraction).
在这种编码方式下, 编码的一部分, 比如高8位作为指数编码空间, 剩余的空间用来编码分数.
4 = 8 * 0.5 = pow(2, 3) * 0.5 = 0x03 << 24 | 0x800000 = 0x03800000
12 = 16 * 0.75 = 0x04c00000
以4为例首先将其转为科学计数法(pow(2, 3) * 0.5), 然后分别对指数部分与分数部分编码, 最后拼接在一起得到最终值.
这种编码方式下分数的每位的权重(对应实际的数值)是非固定的(由指数位决定), 因此也被称为浮点数.
IEEE754是一种实现浮点数及其运算的标准, 它被广泛使用在许多现代处理器架构中, 其文档可以参见这里.
IEEE754的编码方式与上文稍稍有些不同, 其编码公式为(pow(2, exponent - bias) * (1 + fraction)), 这里以常见的单精度(float)与双精度(double)为例:
| type | length | exponent | fraction |
|---|---|---|---|
| float | 32 | 8 | 24 |
| double | 64 | 11 | 53 |
如上表所示float类型的指数位8位, 即指数范围0 - 255. 为支持小于1的数值编码还需要减去一个指数偏移值(bias), 其大小为(pow(2, exponent - 1) - 1)(取一半再减1). 因此float实际所能表达的指数范围是-127 - 128.
float类型的分数位24位, 其中1位符号位(占据编码最高位). 因此float类型的精度是2的-23次. 注意IEEE754规定了fraction仅包含小数部分, 即运算结果还需要加1.
从网上拖的图为例:
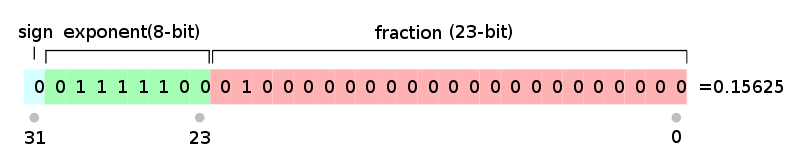
0.15625 = 1.25 / 8 = pow(2, -3) * 1.25 = pow(2, 124 - 127) * (1 + 0.25) = 124 << 23 | 0x200000 = 0x3e200000
首先将0.15625转换为科学计数法, 得到指数部分为(1 / 8), 分数部分(1 + 0.25). 由于指数需要减去偏移值, 所以被编码的指数值为(-3 + 127) = 124, 而分数部分被编码值为0.25, 最终拼接值为0x3e200000.
写个case证明一下:
[23:33:52] hansy@hansy:~/testcase$ cat 1.c
#include <stdlib.h>
#include <stdio.h>
int main() {
float a = 0.15625;
int *pa = &a;
printf("%x\n", *pa);
a = 0.25;
printf("%x\n", *pa);
return 0;
}
[23:34:00] hansy@hansy:~/testcase$ gcc 1.c -w && ./a.out
3e200000
3e800000
浮点数的算术运算
IEEE754要求浮点数在做算术运算时需要首先对齐到同一指数位, 然后再做运算, 对齐后做运算的过程会丢失精度. 让我们来看个例子:
[00:47:18] hansy@hansy:~/testcase$ cat 1.c
#include <stdlib.h>
#include <stdio.h>
int main() {
float a = 1.00001;
float b = 100.0;
int *pa = &a;
int *pb = &b;
printf("%x\n", *pa);
printf("%x\n", *pb);
a += b;
printf("%x\n", *pa);
printf("%f\n", a);
return 0;
}
[00:47:21] hansy@hansy:~/testcase$ gcc 1.c -w && ./a.out
3f800054
42c80000
42ca0001
101.000008
1.00001与100.0相加, 结果不是101.00001, 也不是101.00000, 而是101.000008, 这是为什么呢?
1.00001对应的指数位为0(指数编码127), 分数位为0x54(84 / (1 << 23)). 100.0对应的指数位为6(指数编码133), 分数位为0x480000(1.5625 = 1 + 0.5625 = 1 + (0.5 + 0.0625)).
由于两者量级不同, 1.00001首先会对阶到同一指数, 1.00001指数位增加6, 因此对应的分数部分右移6位(指数权重扩大需要对应分数位降低权重), 相当与变成了0x42800000 | 0x1.
然后分数部分两者相加0x480000 + 0x1 = 0x480001, 注意前面计算的1.00001的分数部分并不包含那个1, 实际上移位后1也需要转换到对应的分数编码0x20000(指数位为6, 需要右移6次, 即1 << (23 - 6)), 所以最终分数编码为0x4a0001. 转换为float数值为101.00008
从这个例子可以看出, 浮点运算在做对阶操作过程中会产生精度的丢失. 当参与运算的两个数指数相差很大, 大到超过分数编码长度时, 对阶后分数部分为0.
回到开头
为什么最终答案是1024? 因为float分数编码23+1位(23位分数编码加1对应的整型位), 所以当两者的阶码超过24时相加不会再改变结果. 而0.000061的指数是-15, 因此当res到达pow(2, 10)后0.000061被彻底忽略.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号