2025年高一上学期停课备赛笔记

前言

本文章只记录了模拟赛的题目，其实每日还做了其他的题，不在此做记录。

* 表示未完成的题目，^ 表示待补博客的题，~ 表示自我感觉经典的题目。

09/01

经过讨论后得到的：

\(9\) 月半停（下午和晚上），\(10,11\) 月全停。

T1

题面

给定一个序列 \(a\)，令 \(S\) 为 \(a\) 序列的一个子集，称其合法，当且仅当存在一个 \(S\) 的子集 \(T\)，使得 \(|T| = |S| - k\)，且 \({\sum_{{i} \in {T}}{a_i}} \ge {m}\)。

求对于 \(\forall {{k} \in {[0,n]}}\) 时合法集合 \(S\) 的数量。

\({n,m,a_i} \le {3000}\)

Solution

定义 \(f_{i,j}\) 为前 \(i\) 个数组成集合 \(S\)，\(S\) 中权值和为 \(j\) 的子集数量，转移就是正常的背包；

反过来想，\(|T| = |S| - k\)，也就是 \(|S| = |T| + k\)，此时 \(k \in [0,n - i]\)，乘上对应的组合数并记录贡献，即：

\[g_k = g_k + {(f_{i,m} - f_{i-1,m})} \times {\binom{n-i}{k}} \]

复杂度为 \(O(n ^ 2)\)。

注意：这里权值和 \(\ge {m}\) 的方案也都计入 \(f_{i,m}\) 中。

Reflect

做的时候一直往如何对集合 \(|S|\) 直接进行背包去想，但必须要顾及集合大小，取值和，转移状态达到三维；思路的突破口在于想到从 \(|T|\) 入手，用组合数解决集合大小这一维度。

T2

题意

随机给出一张 \(n\) 个点 \(m\) 条边的无向简单联通图，点 \(1\) 到 \(n-1\) 初始值为 \(1\)，给定一个长度为 \(n-1\) 的排列 \(p\)，第 \(i\) 轮，从节点 \(p_i\) 出发到 \(n\)，求路径点权和最小值。

\({n} \le {7.5} \times {10 ^ 4},{n-1} \le {m} \le {2n}\)

时限：\(4s\)

Solution

将 \(1\) 到 \(n\) 所有点的入边权值设置为 \(1\)，，从 \(n\) 开始跑反图的最短路 \(dis_i\)，每次改变 \(p_i\) 的入边权值，再从 \(p_i\) 开始在反图上搜索。

由于每个点松弛过后，距离会减少 \(1\)，因为随机一棵树，直径期望值是 \(O(\sqrt{n})\) 级别的，所以复杂度为 \(O(m \sqrt{m})\)。

我们发现一个问题，如果每次都用 dijkstra 松弛，时间复杂度带 \(\log\)。

Tip ：当边权都为 \(0/1\) 时，可以运用 01bfs 将复杂度优化成线性。

T3 P10681 [COTS 2024] 奇偶矩阵 Tablica

题意

考虑只包含 \(0\) 和 \(1\) 的 \({n} \times {m}\) 矩形，称满足以下条件的矩阵是好的：

\(\forall {{1} \le {i} \le {N}}\)，\(\displaystyle \sum_{j=1}^{M}{A_{i,j} \in {\{1,2\}}}\)；
\(\forall {{1} \le {j} \le {M}}\)，\(\displaystyle \sum_{i=1}^{N}{A_{i,j} \in {\{1,2\}}}\)。

求好的矩阵的数量。

\({1} \le {N,M} \le {3000}\)

Solution

考虑行向列连边，相当于左边有 \(n\) 个点，右边有 \(m\) 个点，要求无重边，且每个点的度数为 \([1,2]\)。

假设度数为 \(2\) 的球有 \(j\) 个，那么相当于把 \(n+j\) 个球放入 \(m\) 个盒子中，设 \(f_{i,j}\) 表示将 \(i\) 个球放入 \(j\) 个盒子中的方案数，有：

\[f_{i,j} = f_{i-1,j-1} \times {\binom{n}{1}} + f_{i-2,j-1} \times {\binom{n}{2}} \]

因为左边的点本质相同，所以贡献为 \(\Large {\frac{f_{n+j,m}}{{2} ^ {j}}}\)。

发现这样计算可能会出现重边，考虑枚举重边的个数 \(i\)，则答案为：

\[\sum_{i=0}^{n}{ \binom{n}{i} \binom{m}{i} i! (-1) ^ i \sum_{j=0}^{n-i}{\frac{1}{2^{i+j}} \binom{n-i}{j} f_{n-i+j,m-i}}} \]

复杂度为 \(O(n^2)\)，注意勤取模，特别是负数取模的处理。

T4 P11945 [KTSC 2025] 军事基地 / safezone

题意

给定 \(n\) 个矩形，定义两个矩形连通为两个矩形有交点，求出每个矩形所在连通分量。

Solution

考虑对 \(x\) 轴进行扫描线，需要支持加入、删除线段以及合并相交线段的编号，合并操作可以用并查集维护。

当往线段树上加入一条线段时，线段会被拆成若干个区间，与这些区间的祖先和儿子上拆出的其他线段的编号合并。

对于祖先的合并是简单的，在拆分线段的过程中暴力合并即可；

对于儿子的合并考虑使用懒标记，在删除线段时进行合并，具体的，在线段树的每个节点上建立队列维护懒标记，表示子树内加入时间在 \(x\) 之前的线段会和后面加入的某条线段的编号产生合并，注意懒标记不需要下传；

定义一个矩阵的加入时间为其左线段加入线段树的时间（或者左线段的横坐标）；

在删除线段的时候，对经过的祖先上的懒标记队列所记录的线段编号中，加入时间比当前删除线段所在矩形的加入时间更晚的线段进行合并，并将这些线段全部弹出队列，只需要保留加入时间最晚的线段信息以便后续合并即可。

太干涩了，举个栗子，如下图中的若干个矩形，其中蓝色矩形的线段是最小的，区间值域为 \([5,6]\)，在删除其右线段的过程中，必然会经过祖先区间 \([1,8],[5,8]\)，当到区间 \([5,8]\) 时候，这个区间的队列懒标记中存储了灰、红、黄、绿、紫色的矩形所在连通分量的编号。

灰色矩阵的加入时间比蓝色矩阵的加入时间更早，不需要合并；而后面的四个矩阵则需要和蓝色矩阵的编号合并，并弹出队列，但还要将最晚加入的矩阵（紫色）再次加入队列，用于后面的合并操作。

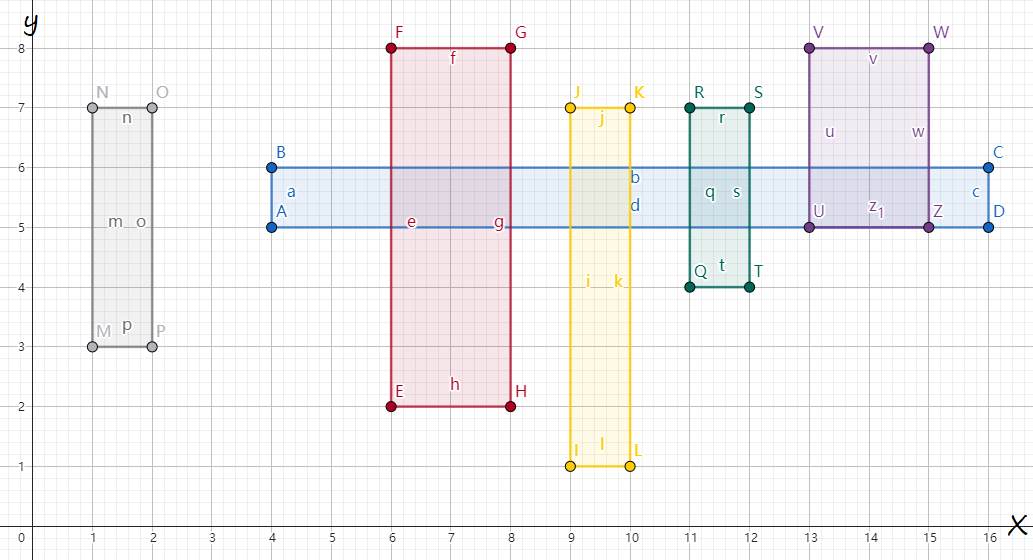
P11945

时间复杂度为 \(O(n\alpha{(n)}\log {n})\)；空间复杂度为 \(O(n \log {n})\)，瓶颈在懒标记队列，最多会加入 \(n \log {n}\) 个点。

09/04

T1 P13532 [OOI 2023] Buying gifts / 购买礼物

题意

给定 \(n\) 对数对 \((a_i,b_i)\)，从每个数对选出其中的一个数，最后使得取出的 \(a_i\) 与 \(b_i\) 的最大值之差最小。

\(0 \le {n} \le {2} \times {10 ^ 5}\)

Solution

将 \(n\) 对数对按 \(a\) 从小到大排序，枚举 \(a_i\) 为选出的 \(a\) 中最大的数，那么 \(j > i\) 的 \(b_j\) 都必须选，这里很容易想到用最大后缀来维护；

那么对于 \(j < i\) 的情况，可以选 \(a_j\) 也可以选 \(b_j\)，选 \(a_j\) 对答案没有影响，考虑选 \(b_j\) 的情况，为了使差值最小，那就是找到最后一个 \(\ge {a_i}\) 的 \(b_k\)，或者第一个 \(\ge {a_i}\) 的 \(b_k\)，需要满足 \(b_k\) 大于后缀最大值，可以直接用 set 维护，也可以用权值线段树。

Reflect

可以用其他简单的数据结构或者方法代替线段树的时候，尽量写得简单一些。

T2 P6583 回首过去

题意

给定正整数 \(n\)，求出有序整数对 \((x,y)\) 的个数，满足 \({1} \le {x,y} \le {n}\) 且 \(\Large {\frac{x}{y}}\) 可以表示为十进制有限小数。

\({1} \le {n} \le {10 ^ {12}}\)

Solution

先来想一下一个可以表示为十进制有限小数的分数，必然可以通过不断地乘以 \(10\) 变成一个整数，分析一下可以得到其本质就在于分数进行约分后分母依旧存在质因子 \(2,5\)。

那么我们把 \(\Large {\frac{x}{y}}\) 分解成 \(\Large {\frac{bc}{ac}}\)，其中 \(a\) 只含有 \(2,5\) 两种因子，\(b\) 不含有 \(2,5\) 两种因子，\(c\) 为任意的整数（相当于约分）。

依次在 \([1,n]\) 内枚举 \(a\)，这里也可以对 \(a\) 的数进行预处理，再在合法范围 \([1,\lfloor {\frac{n}{a}} \rfloor]\) 内枚举 \(c\)，然后合法的 \(b\) 个数是 \(\lfloor {\frac{n}{c}} \rfloor\)，这样做的时间复杂度为 \(O({n} ^ {2})\)；

尝试通过转换枚举顺序来达到优化的目的，先枚举 \(c\)，\(b\) 的取值范围依旧是 \([1,\lfloor {\frac{n}{c}} \rfloor]\)，而 \(a\) 的取值就变成了 \([1,\lfloor {\frac{n}{c}} \rfloor]\) 中只含有 \(2,5\) 两种因子的数，也就是对于每个 \(c\)，记合法的 \(a\) 的个数为 \(d\)，那么贡献就为 \(d \times {\frac{n}{c}}\)，时间复杂度为 \(O(n)\)；

记 \(f(x)\) 为在 \([1,x]\) 中只含有 \(2,5\) 两种因子的数的个数，那么上文的式子等价于：

\[f(\lfloor {\frac{n}{c}} \rfloor) \times {\lfloor {\frac{n}{c}} \rfloor} \]

这是一个经典的整除分块问题，但是 \(c\) 的取值是不含有 \(2,5\) 两种因子的数，可以用容斥思想，对于一段区间 \([l,r]\)，设 \(g(x)\) 为区间 \([l,r]\) 中 \(x\) 的倍数的个数，那么合法的个数为 \(cnt = g(1) - g(2) - g(5) + g(10)\)，区间 \([l,r]\) 对答案的贡献为 \(cnt \times f(\lfloor {\frac{n}{c}} \rfloor) \times {\lfloor {\frac{n}{c}} \rfloor}\)，时间复杂度优化到 \(O(\sqrt{n})\)。

Reflect

连一些最基本的数学概念性问题都没搞懂？？？

T3 P10207 [JOI 2024 Final] 马拉松比赛 2 / Marathon Race 2

题意

在一条长为 \(L\) 的路上放了 \(N\) 个球，所在位置分别为 \(X_i\)，取一个球的时间为 \(1\) 秒，拿着 \(x\) 个球移动一个单位需要 \(x + 1\) 秒，且途中不能把球放下。

\(Q\) 次询问 \((S_j,G_j,T_j)\)，求从 \(S_j\) 出发，终点为 \(G_j\)，在 \(T_j\) 秒内是否能取完所有的球。

\({1} \le {N,L,Q} \le {5 \times {{10} ^ {5}}}\)

\({0} \le {X_i,S_j,G_j} \le {L},{1} \le {T_j} \le {5 \times {{10} ^ {5}}}\)

Solution

每个球先按照顺序排序并离散化后，有球的位置的个数为 \(n\)，分别为 \(a_i\)，利用前缀和 \(cnt_i\) 为前 \(i\) 个位置的总球数；

很明显的一个结论，取的第一个球必然是在 \(a_1\) 或者 \(a_n\) 的，进而想到用 \(f_{l,r,0/1,0/1}\) 表示从 \(1/n\) 出发，已经取了 \([1,l)\) 和 \((r,n]\) 位置上的球，当前位于 \(l/r\) 位置时的最短时间，令 \(x\) 为当前状态移动一个单位所需要的时间 \(cnt_{a_{l-1}} + cnt_{n}-cnt_{a_{r}} + 1\)，则有转移为：

移动到 \(l\) 时，\(f_{l,r,k,0} = \min {\{f_{l,r,k,0} + x \times {(a_l - a_{l-1})},f_{l,r,k,1} + x \times {(a_{r+1} - a_{l})}\}}\)
移动到 \(r\) 时，\(f_{l,r,k,1} = \min {\{f_{l,r,k,0} + x \times {(a_{r} - a_{l-1})},f_{l,r,k,1} + x \times {(a_{r+1} - a_{r})}\}}\)

（这里的 \(k\) 为 \(0/1\) 的时候，表示从 \(1/n\) 出发）

观察一下题意，询问的时间限制 \(T_j\) 的最大值为 \(5 \times {{10} ^ {5}}\)，而移动一个单位的时间 \(x\) 随着拿着球数量的增多而增多，最后的时间至少为 \(\frac{n(n+1)}{2}\)，因此 \(n\) 只有 \(O(\sqrt{T})\) 级别，时间复杂度为 \(O({n} ^ {2})\) 完全可以过掉。

最后用二分找到离 \(G_j\) 最近的点 \(p\)，取 \(f_{p,p,0/1,0/1}\) 再加上从 \(S_j\) 到 \(1/n\) 和 \(p\) 到 \(G_j\) 的时间即可，注意还要加上取所有球的时间 \(cnt_n\)。

Reflect

一开始想把 \(n\) 个球按位置以 \(S_j,G_j\) 分为三部分进行贪心，\([S_j,G_j]\) 必然是最后取最优，虽然这个贪心可能是错的；

后面就应该要想到第一个取的球要么从最左边或者最右边的球开始，再考虑用这个写dp状态。

还要多关注数据之间的关系，考虑是否可以缩小数据，弱化题目。

T4 P10208 [JOI 2024 Final] 礼物交换 / Gift Exchange

题意

有 \(n\) 个人，第 \(i\) 个人会送出价值为 \(a_i\) 的礼物，且要求收到的礼物价值不低于 \(b_i\)，保证 \(b_i < a_i\)。

\(q\) 次询问 \((l_j,r_j)\)，问区间 \([l_j,r_j]\) 内的人是否能互送礼物。

\({2} \le {n} \le {5 \times {{10} ^ {5}}},{1} \le {b_i} < {a_i} \le {2n}\)

\({1} \le {q} \le {2 \times {{10} ^ {5}}},{1} \le {l_j} < {r_j} \le n\)

Solution

由于 \(b_i < a_i\)，我们不妨将每个人表示成 \([b_i,a_i]\)，也意味着对于 \((i,j)\)，只有其区间有交，两人才能互送礼物，且称 \((i,j)\) 连通。

考虑询问区间 \([l_j,r_j]\)，所有 \(i \in {[l_j,r_j]}\) 的区间形成了若干个连通分块；

把每一个连通分块单独拿出来分析，并按 \(a\) 从小到大排序，当连通分块的大小 \(\ge 2\) 时，其中最后一个人（\(a\) 最大）可以把礼物送给连通分块里任意一个人，不妨直接送给第一个人；根据上述连通的性质，从第一个人到倒数第二个人都可以把礼物送给后面一个人，相当于送礼物和收礼物的过程形成了一个闭环，这样连通分块里的人都能够互送礼物。

那么反过来想，如果要不能够互送礼物，就只能是单独一个人的连通分块，题目转化成快速求 \([l_j,r_j]\) 内是否存在 \([b_i,a_i]\) 与其他区间没有交集，不妨设 \(L_i,R_i\) 分别表示 \(i\) 左边/右边第一个与其有交集的人的编号，如果 \(\not {\exists {{L_x} < {l_j} \le {x} \le {r_j} < {R_x}}}\)，那么区间 \([l_j,r_j]\) 内的人可以互送礼物；\(L_i,R_i\) 可以先对 \(a\) 排序，再用值域线段树维护。

最后想如何判断 \(\not {\exists {{L_x} < {l_j} \le {x} \le {r_j} < {R_x}}}\)，考虑使用扫描线，支持区间加减和单点查询：

当遇到 \(l_j\) 时，判断当前的线段树里是否存在 \({x} \le {r_j} \le {R_x - 1}\)，那也就是查询 \(r_j\) 上是否为 \(0\)，所以在 \(L_x\) 时插入区间 \([x,R_x - 1]\)（区间加 \(1\)），在 \(x\) 时删除。

注意：扫描到位置 \(x\)，操作顺序为：先查询再插入和删除。

复杂度为 \(O(n \log {n})\) 的。

Reflect

遇到 \(b_i < a_i\) 这种性质的东西，尝试用区间来表示；区间问题时有连通的性质不妨拆出来单独讨论；对于类似于上面最后的判定式可以往扫描线想。

09/06

T1 CF1497D Genius

题意

给定 \(n\) 个问题，第 \(i\) 问题有 \(a_i = {{2} ^ {i}},b_i,c_i\)。

解决 \(i\) 问题后解决 \(j\) 问题需要满足 \({x} < {|a_i - a_j|}\) 且 \(b_i \ne b_j\)；

解决完问题后 \(x = |a_i - a_j|\)，获得 \(|c_i - c_j|\) 分，\(x\) 初始为 \(0\)，求可获得的最高分数。

\({1} \le {n} \le {{5} \times {{10} ^ {3}}},{1} \le {b_i} \le {n},{1} \le {c_i} \le {{10} ^ {9}}\)

Solution

\(f_i\) 表示以问题 \(i\) 为结尾的路径可以获得的最高分数，转移条件为路径的边权 \(|a_i - a_j|\) 单调递增，\(f_i = f_j + |c_i - c_j|\)。

由于 \(a_i = {2} ^ {i}\)，对于 \(i \in [2,n]\)，前面 \(i - 1\) 个数都可以转移过来，因为 \(a_i - a_{i-1} = {{2} ^ {i}}\) 都已经大于前面任意两个数的差了；对于 \(L < R < i\)，都有 \({{2} ^ {i}} - {{2} ^ {L}} > {{2} ^ {i}} - {{2} ^ {R}}\)，也就是说，如果倒序枚举 \(j \to i\) 的转移，顺带处理 \(i \to j\) 进行转移，那么上一次（枚举到 \(j - 1\) 时）的 \(x\) 必然都比 \(a_i - a_j\) 小，直接暴力转移式子即可，有点妙啊。

最后总结就是一维 \(i\) 顺序枚举，另一维 \(j\) 倒序枚举，直接双向转移就可以了，时间复杂度为 \(O(n ^ 2)\)。

T2

题意

有 \(n\) 个人排成一列，游戏进行多个回合，每一回合淘汰在第 \({i} \times {k} + 1,i \in {\mathbb {N}}\) 位置上的人，直到最后只剩下一个人，求问这个人的编号。

\({2} \le {n,k} \le {{10} ^ {12}}\)

Solution

设 \(G(n,k)\) 表示最后留下来的人的编号，令 \(z = G(n - \lceil {\frac{n}{k}} \rceil,k)\)，考虑如何能推回去，由于上一轮游戏是每隔 \(k - 1\) 就淘汰一个人，则有 \(G(n,k) = z + \frac{z}{k-1}\)，显然的，\(G(1,k) = 1\)。

容易发现在推导过程中不同的 \(\lceil {\frac{n}{k}} \rceil\) 的个数不会超过 \(\sqrt{n}\)。

证明：若 \({k} \le {\sqrt{n}}\)，则每次被删掉的人数都 \(\ge {\sqrt{n}}\)，至多只会删 \(\sqrt{n}\) 次，意味着最多只会出现 \(\sqrt{n}\) 次不同的 \(n\)，\(k\) 不变，\(\lceil {\frac{n}{k}} \rceil\) 的个数不会超过 \(\sqrt{n}\)；若 \({k} \ge \sqrt{n}\)，那显然成立。

根据上面的结论，可以快速算出 \(G(n,k)\) 到达 \(G(1,k)\) 经过的轮数 \(s\)，具体的，设 \(\lceil {\frac{n}{k}} \rceil = x\)，找到最小的 \(l\) 满足 \(\lceil {\frac{l}{k}} \rceil = x\)，即 \(l = k \times {(x-1)} + 1\)，则减了 \(\lceil {\frac{n - l + 1}{x}} \rceil\) 次的 \(x\) 使得 \(n < l\)，把其贡献进 \(s\) 的次数里。

那么从 \(G(1,k)\) 反推回 \(G(n,k)\) 也是同理的，\(\lceil {\frac{z}{k-1}} \rceil = x\) 的个数也是 \(O(\sqrt{n})\) 级别的，找到最大的 \(r\)，满足 \(\lceil {\frac{r}{k-1}} \rceil = x\)，即 \(r = {x} \times {(k-1)}\)，则加了 \(k = \lceil {\frac{r - z + 1}{x}} \rceil\) 次 \(x\) 使得 \(z > x\)；上面算出的总轮数为 \(s\) 不断减去 \(k\)（注意 \(k\) 不能超出 \(s\)），直到 \(s\) 为 \(0\) 时的 \(z\) 就是最后的编号。

时间复杂度为 \(O(\sqrt{n})\)。

T3 P11340 [COI 2019] TENIS

题意

\(n\) 个选手参加比赛，有三种不同的球场，每个人在不同的球场的能力值会不一样，并给定在每种球场上能力值从强到弱的排名编号。

一共会进行 \(n-1\) 场比赛，每场比赛可以挑选任意两个人在特定的场地上比赛，在这种场地上能力值强的人会淘汰掉较弱的人。

接下来 \(q\) 行，每行表示一个事件：

1 x：表示选手 \(x\) 能否夺冠；
2 p a b：表示交换第 \(p\) 个排名表中选手 \(a\) 和选手 \(b\) 的排名位置。

\({1} \le n,q \le {{10} ^ {5}},{1} \le {x,a,b} \le {n},{1} \le {p} \le 3,a \ne b\)

Solution

把三个场地的排名看成一个二维数列，显然的，第一列的每个编号的选手都能够夺冠；

接着讨论第二列的选手，由于第一列的选手可以淘汰掉后面所有人，假定第一列的选手编号都不一样，分别为 \(a,b,c\)，第二列的编号分别为 \(i,j,k\)：

那么对于选手 \(j\) 来说，在场地二能够淘汰掉选手 \(a\)，按照这个思路，只需要让 \(a\) 淘汰掉除去 \(j\) 的其他选手，最后让 \(j\) 淘汰掉 \(a\)，那么 \(j\) 就可以夺冠了，那么 \(i,k\) 是同理的。

反向思考什么情况是不满足上述情况的，那就是当第 \(x\) 列的选手在每种场地都无法淘汰掉前面的选手时，第 \(x\) 列的选手都不可能夺冠，同样的，第 \(x\) 列后面的所有选手都无法夺冠。

由此我们得到了一个结论：找到一个最小的 \(x\)，使得 \([1,x]\) 列中，每个数出现的次数都为 \(3\)，那么前 \(x\) 列的所有选手都能夺冠。可以用数学归纳法证明吧...

现在考虑如何动态快速寻找 \(x\)，不妨令 \(p_{i,1/2/3}\) 表示选手 \(i\) 在三种场地上的排名，\(l_i，r_i\) 分别表示排名的最小值/最大值，即 \(l_i = \min {\{p_{i,1},p_{i,2},p_{i,3}\}},r_i = \max {\{p_{i,1},p_{i,2},p_{i,3}\}}\)，对区间 \([l_i,r_i)\) 的数加 \(1\)，查询时找到最小的 \(x\)，且 \(x\) 位置上的数为 \(0\)，用线段树上二分来维护，复杂度为 \(O(n \log {n})\)。

Reflect

看到有淘汰关系类型的题，其实还应该想到连边，本题也可以在连完边后的有向图上缩点后进行分析性质。

T4 P12445 [COTS 2025] 数好图 / Promet

题意

给定正整数 \(n\)，对于 \(k \in [0,n]\)，求出满足以下条件的简单有向图的数量：

图中仅包含 \({i} \to {j}\)（\({1} \le {i} < {j} \le {n}\)）的边；
满足以下条件的点 \(u\) 恰好有 \(k\) 个：
- 存在 \(1\to u\) 和 \(u\to n\) 的路径。

\({2} \le {n} \le {2000}\)

Solution

先讨论 \(k = n\) 时，先考虑这样构造图，钦定 \(i\) 必须向 \([i+1,n]\) 中的若干个点连边，则有 \({2} ^ {n - i} - 1\) 种连边方案，保证了每个点都能达到 \(n\)。

接着构造从 \(1\) 能够到达所有点的连边，如果 \(1\) 不能到每个点，则至少有一个点的入度为 \(0\)，考虑容斥。

\(f_{i,j}\) 表示钦定倒数第 \(i\) 个点（也就是第 \(n - i + 1\) 个点）的入度为 \(0\)，从倒数第 \(i - 1\) 个点到倒数第 \(1\) 个点中至少有 \(j\) 入度为 \(0\) 的点时的连边方案数（注意点 \(n\) 的入度始终都不为 \(0\)）。

\(f_{1,0} = 1\)，讨论第 \(i - 1\) 个点的入度是否为 \(0\)，无论如何 \(i\) 都需要向后连边，得到转移式子：

\[f_{i,j} = f_{i-1,j} \times {({2} ^ {(i - 1) - j} - 1)} + f_{i-1,j-1} \times {({2} ^ {(i - 1) - j} - 1)} \]

令 \(F_i\) 表示在有 \(i\) 个点的图中，\(k = i\) 的答案，由于容斥可得：

\[F_i = \sum_{j=0}^{i-1} {(-1) ^ {j}} \times {f_{i,j}} \]

对于更小的 \(k\)，其实就是往 \(F_k\) 中加入 \(n-k\) 个不合法的点，考虑点 \(i\)：

\(1\) 类点： \(i\) 满足 \({1} \to {i},{i} \to {n}\) 的路径都有，也就是 \(F_k\) 中的点；
\(2\) 类点：\(i\) 是加入的点，满足 \({1} \to {i},{i} \not \to {n}\)；
\(3\) 类点：\(i\) 是加入的点，满足 \({1} \not \to {i}\)。

其中 \(1,n\) 一定是 \(1\) 类点，依据第 \(i\) 类点被前面的第 \(j\) 类点连边后还是否满足其性质，来考虑这些点之间的连边：

后面的 \(1\) 类点可以被前面的 \(3\) 类点连；
后面的 \(2\) 类点可以被前面的 \(1,2,3\) 类点连，且必须被 \(1,2\) 类点连；
后面的 \(3\) 类点可以被前面的 \(3\) 类点连。

观察发现，前面的 \(3\) 类点可以向后面的任意点连边，设 \(g_{i,j}\) 表示 \([i,n-1]\) 中有 \(j\) 个 \(3\) 类点的连边方案数；

从后往前枚举，\(g_{n,0} = 1\)（并没有实际意义），有转移：

\[g_{i,j} = g_{i+1,j} + g_{i+1,j-1} \times {{2} ^ {n - i}} \]

这里注意 \(3\) 类点不一定需要向后面的点连边，故为 \({{2} ^ {n - i}}\)。

最后考虑 \(2\) 类点，其连边与 \(1\) 类点的数量有关，设 \(h_{i,j}\) 表示考虑完前 \(i\) 个 \(1\) 类点，在第 \(1\) 个 \(1\) 类点到第 \(i + 1\) 个 \(1\) 类点之间插入了 \(j\) 个 \(2\) 类点的连边方案数，\(h_{0,0} = 1\)，有转移：

\[h_{i,j} = h_{i-1,j} + h_{i,j-1} \times {({2} ^ {i + j - 1} - 1)} \]

定义 \(ans_i\) 表示在有 \(n\) 个点的图中，\(k = i\) 时的连边方案数。

\(i,j\) 分别枚举 \(1,2\) 类点的个数点 \(n\)，注意到 \(h_{i,j}\) 的定义是指往第 \(1\) 个到第 \(i+1\) 个 \(1\) 类点中插入 \(2\) 类点，当钦定第 \(i\) 个 \(1\) 类为点 \(n\) 时，此时连边方案数应为 \(h_{i-1,j}\)；由于点 \(1\) 不属于 \(3\) 类点，故 \(3\) 类点的贡献为 \(g_{2,n-i-j}\)，综上有转移：

\[ans_i = F_{i} \times {\sum_{j=0}^{n-i} {h_{i-1,j} \times g_{2,n-i-j}}} \]

最后对于 \(k = 0,1\) 的情况特殊处理：

\(k = 1\) 时，显然答案为 \(0\)，因为但凡存在 \({1} \to {x} \to {n}\) 的路径，\(1,n\) 都属于答案。
\(k = 0\) 时，先构造出任意的图，连边方案数为 \({2} ^ {\frac{n(n-1)}{2}}\)，再减去 \(k \ge 2\) 的合法连边方案数即可。

复杂度为 \(O(n ^ 2)\)。

09/11

T1

题意

int a[MAXN];
int partition(int l, int r){
	int x = a[r],i = l;
	for(int j=l;j<r;j++){
		if(a[j] < x){
			swap(a[i], a[j]);
			++i;
		}
	}
	swap(a[i], a[r]);
	return i;
}
void Qsort(int l, int r, int h){
	if(l<r && h>1){
		int m = partition(l,r);
		Qsort(l,m-1,h-1);
		Qsort(m+1,r,h-1);
	}
}

\(T\) 次询问，每次询问给定 \(n,k\)，问有多少个大小为 \(n\) 的排列 \(a\) 在调用 Qsort(1,n,k) 能变成有序。

\({T} \le {500},{1} \le {n,k} \le {300}\)

Solution

先分析清楚 Qsort 的作用，观察可得其实就是将 \(a_r\) 排到有序的位置，左边都是 \(< a_r\) 的数，右边都是 \(> a_r\) 的数，且左右两边的数之间都是按照原序列的位置排序；再进而递归处理左右两边的序列，\(k\) 限制了递归的层数。

考虑预处理答案，\(f_{i,j}\) 大小为 \(i\)，递归 \(j\) 层可以变成有序的排列个数。

枚举当前层 \(a_r\) 的值 \(l\)，那么就是左右两个子问题的方案数做乘法原理；注意递归进入子问题前该层还需要对 \(l\) 排序，相当于左右按顺序互相交叉，可以用插板法：

\[f_{i,j} = \sum_{l=1}^{i} {{f_{l-1,j-1}} \times {f_{i-l,j-1}} \times {\binom{i-1}{l-1}}} \]

复杂度为 \(O(n ^ 3)\)，瓶颈在预处理 \(f\)。

一个小小小疑惑：查询都为 \(O(T)\) 了，\(T\) 的范围还取那么小，搞得我一开始以为不能预处理，要 \(O(n ^ 2)\) 在线求方案数...

Reflect

其实已经想到预处理和dp的状态和转移思路了，就是少了最后的插板法，漏想了排序前左右两边可以互相交叉。

T2 CF1975D Paint the Tree

题意

给定一个 \(n\) 个点的树，初始每个点都是白色的，A 和 B 分别位于 \(a\) 和 \(b\)，每一步会进行以下两个操作：

A 移动到相邻的点，若该点是白色的，则将其染成红色；
B 移动到相邻的点，若该点是红色的，则将其染成蓝色。

将所有顶点都染成蓝色所需要的最少步数。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}}\)

Solution

找到 \(a\) 和 \(b\) 之间最短路径的中点 \(c\)，以 \(c\) 为根求跑完整棵树的最短路。

上面的结论可以用交换论证法简单证明，不再赘述。

最后求跑整棵树的最短路不必用树形 DP，小技巧吧，每条边都必然要经过两次，也就是 \(2(n-1)\)，由于不用返回起点，再找到以 \(c\) 为根的树中的最大深度 \(d\)，最短路长度就为 \(2(n-1) - d\)。

T3 P12546 [UOI 2025] Convex Array

题意

给定一个长度为 \(n\) 的序列 \(a\)，判断是否存在一种元素排列 \(b\)，使得对于每个 \({2} \le {i} \le {n-1}\)，都满足 \({b_{i-1} + b_{i+1}} \ge {{2} \times {b_i}}\)。

\({3} \le {n} \le {{3} \times {{10} ^ {5}}},{0} \le {a_i} \le {{10} ^ {9}}\)

Solution

\({b_{i-1} + b_{i+1}} \ge {{2} \times {b_i}} \iff {b_i - b_{i-1}} \le {b_{i+1} - b_i}\)，也就是说排列 \(b\) 中相邻两点间的斜率单调不降，表现为下凸包。

对 \(a\) 序列排序，最后的排列中一定是 \(a_1\) 在下凸包的最低点，左右两边分成两个独立的部分，且差分序列单调不降。

从小到大往左右序列插入 \(a\)，前提条件只和该序列中的最大和次大值有关，于是设 \(f_{p,q,l,r}\) 表示考虑到第 \(i\) 个时，是否能做到左序列的最大值 \(p\) 和次大值 \(q\)，右序列的最大值 \(l\) 和次大值 \(r\)。

由于题目不要求计数，对于左右序列的顺序不作区分，发现 \(p,l\) 中必然有一个是 \(i\)，不妨钦定 \(p\) 为 \(i\)，且 \(i\) 位于左序列，也就是 \(f_{i,q,l,r}\)，暴力转移，时间复杂度为 \(O(n ^ 4)\)。

\(i - 1\) 也必然在状态中，时间复杂度降为 \(O(n ^ 3)\)。

接下来讨论 \(i - 2\) 的分布：

在左序列中：
- \(\{(i,i-1),(x,y)\}\)
- \(\{(i,i-2),(i-1,x)\}\)
在右序列中：
- \(\{(i,i-1),(i-2,x)\}\)
- \(\{(i,x),(i-1,i-2)\}\)

（其中 \(x,y\) 为未知数）

综上，可以列出三种状态：

\(\{(i,i-1),(f_1,x)\}\) （包括了上面 \(\{(i,i-1),(i-2,x)\}\) 的情况）
\(\{(i,i-2),(i-1,f_2)\}\)
\(\{(i,f_3),(i-1,i-2)\}\)

这里的 \(f,x\) 都是未知数。

考虑插入 \(a_{i+1}\) 时的转移，分讨插入左序列还是右序列，令 \(i' = i + 1\)：

插入左序列（\({2} \to {1}\)）：

\[{\{(i,i-2),(i-1,f_2)\}} \to {\{(i',i'-1),(f'_1 = i'-2,x = f_2)\}} \]
插入右序列（\({2} \to {2}\)）：

\[{\{(i,i-2),(i-1,f_2)\}} \to {\{(i'-1,f'_2 = i'-3),(i',i'-2)\}} \]

同理可推得 \({3} \to {1/2}\) 的转移，并且 \({2/3} \not \to {3}\)，注意在转移前判断插入的判定条件。

当 \(f_2,f_3\) 越大时，与其所在序列中的最大值的差值就越小，也就更易于转移，若最大的 \(f_2,f_3\) 都无法转移的时候，较小的也无法转移，所以只需要维护最大的 \(f_2,f_3\) 状态，用两个变量 \(O(1)\) 维护即可。

接下来考虑状态 \(1\) 的转移，设 \(g_i\) 表示考虑到 \(i\) 时，合法的状态 \(1\) 组成的集合，分类讨论：

插入左边（\({1} \to {1}\)）：\({(i,i-1)} \to {(i',i'-1)}\)，前提是 \({a_i - a_{i-1}} \le {a_{i'} - a_{i'-1}}\)，若不满足，说明 \({{g_i} \cap {g_{i'}} = \emptyset}\)；
插入右边（\({1} \to {3}\)）：\({(f_1,x)} \to {(i',f_1)}\)，前提是 \({a_{f_1} - a_x} \le {a_{i'} - a_{f_1}}\)，即 \(a_{i'} \ge {{2} \times {a_{f_1}} - a_x}\)。

\[\{(i,i-1),(f_1,x)\} \to {\{(i',f'_3 = f_1),(i'-1,i'-2)\}} \]

上文提到 \(f_3\) 只用维护最大，相当于要找到所有满足 \(a_{i'} \ge {{2} \times {a_{f_1}} - a_x}\) 的 \(f_1\) 中的最大值；

令 \(v = {2} \times {a_{f_1}} - a_x\)，利用单调队列的思想，用 map （其实也可以用其他的类似于 set 等数据结构）按 \(v\) 的大小来维护合法集合 \(g_i\) 的单调队列，每次转移时只需要找到前缀 \([1,a_{i'}]\) 中最大的 \(f_1\)；

加入新的点 \((v,f_1)\) 时，把 map 中满足 \({V} \ge {v},{F} \le {f_1}\) 的劣点 \((V,F)\) 给删去，保持单调不减即可。

时间复杂度为 \(O(n \log {n})\)，瓶颈在 map 的 \(O(\log {n})\) 查询，空间复杂度为 \(O(n)\)。

T4 P11516 [CCO 2024] Summer Driving*

点分树？蒟蒻不会，跑了跑了。

09/13

T1 P11662 [JOI 2025 Final] 方格染色 / Grid Coloring

题意

对一个 \({n} \times {n}\) 的网格图染色，给定两个序列 \(a_i,b_i\)，分别表示 \((1,i)\) 和 \((i,1)\) 被染上的颜色，一个格子 \((i,j)\)（\({2} \le {i,j} \le {n}\)）的颜色 \(c_{i,j}\) 为 \(\max{\{c_{i-1,j},c_{i,j-1}\}}\)。

在染色结束后，求被染上的次数最多的颜色编号，以及其染色的次数。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i,b_i} \le {{10} ^ {9}}\)

Solution

很显然能看出来对于格子 \((i,j)\)（\({2} \le {i,j} \le {n}\)），其颜色为矩阵 \((1,1,i,j)\) 中所有格子颜色的最大值（由于 \((1,1)\) 对后面所有的染色没有贡献，这里选择忽略），也为 \(\max {\{\max \limits_{{2} \le {l} \le {i}} {a_l},\max \limits_{{2} \le {r} \le {j}} {b_r}\}}\)。

进而可以想到维护 \(a,b\) 的前缀最大值，得到两个单调不减的序列；然后对于行 \(i\)，该行有 \(\sum_{j=2}^{n} {[b_j \le a_i]}\) 个格子被填上 \(a_i\) 这种颜色；对于列 \(j\) 同理可得 \(\sum_{i=2}^{n} {[a_i \le b_j]}\)，再统计贡献即可。

统计可以用 map，也可以离散化后用数组记录。

时间复杂度为 \(O(n \log {n})\)，瓶颈在排序。

Reflect

当 map 只是用来记录出现次数时，可以换为 unordered_map。

T2 P12576 [UOI 2021] 数字图/AT_arc038_d [ARC038D] 有向グラフと数

dalao hyh 和我说这个 trick 很典也很常用！！！

题意

有一个 \(n\) 个点 \(m\) 条边的连通有向图，每个点 \(i\) 上有一个数字 \(a_i\)，棋子一开始放在点 \(1\) 上，A 和 B 依次移动棋子，两人都可以在自己移动的回合内终止游戏，且游戏最多会进行到 \({10} ^ {100}\) 回合自动结束。

A 希望最大化最终获得的数字，而 B 则希望最小化最终获得的数字，两人都用最优的策略，求游戏结束时将获得的数字。

\({1} \le {n} \le {{2.5} \times {{10} ^ {5}}},{1} \le {m} \le {{5} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}}\)

Solution

博弈论问题，小 trick：

二分答案 \(x\)，将 \({a_i} \ge {x}\) 的点赋值为 \(1\)；反之赋为 \(0\)。

对于二分赋值后的图分析，若点 \(1\) 的权值为 \(1\)，先手必胜；否则先手必然会把棋子移向相邻的权值为 \(1\) 的节点，如果没有这样的点，那么后手必胜。

对于后手的选择明显也同上，最优的策略是把棋子权值为 \(0\) 的点上。

如果出现 \(1,0\) 一直交替出现的路径，也就是形成了环，由于最大的回合数为偶数，所以最后的赢家必然是后者。

发现对于图中所连两个点权值相等的边，其实是不会走的，不妨删去；对于没有出边的点 \(i\)，到 \(i\) 时的先手必输。

考虑 SG 函数，反向建图，直接拓扑排序，对于起始点 \(i\)，显然有 \(SG(i) = 0\)；对于 \(i\) 在原图中的前驱点 \(j\)（即反图中 \(i\) 指向的点），都有 \(SG(j) = 1\)。

思考一下，现在已知的必胜点已经没有意义了，因为从原图上来讲，没有 \(j\) 的前驱 \(k\) 上的先手会无脑选择走到点 \(j\)，从而使得后手赢，所以可以把该轮确定的点 \(j\) 都忽略，而去寻找反图中 \(j\) 指向的没有确定必胜状态的点 \(k\)；

若点 \(k\) 的所有入边都已经遍历完了，还是没有确定必胜，则有 \(SG(k) = 0\)，并把点 \(k\) 加入队列。

最后判断 \(SG(1)\) 是否为 \(1\)，若为 \(1\) 说明游戏结束时获得的数字至少为 \(x\)。

注意一个小问题，如果出现环，且点 \(1\) 在环上，由于环上所有的点都不会入队，所以 \(SG(1)\) 也必然不会被赋为 \(1\)。

时间复杂度为 \(O(n \log {n})\)。

T3 P11986 [JOIST 2025] 救护车 / Ambulance*

蒟蒻不会。

T4 P11303 [NOISG 2021 Finals] Pond

题意

数轴上有 \(n\) 个点，从第 \(k\) 个点出发访问所有点，记首次到达第 \(i\) 个点的时刻为 \(t_i\)，最小化 \(\sum{t_i}\)。

注：给定 \(n - 1\) 个整数 \(d_i\)，表示相邻两点间的距离。

\({2} \le {k} \le {n} \le {{3} \times {{10} ^ {5}}},{1} \le {d_i} \le {{10} ^ {6}}\)

Solution

有一点像前面的那道 P10207 [JOI 2024 Final] 马拉松比赛 2 / Marathon Race 2？但是没有那么好的性质。

对 \(d_i\) 进行前缀和，将其转化为数轴上的点 \(x_i\)。

依旧暴力 dp，\(f_{l,r,0/1}\) 表示已经访问过了 \([l,r]\) 内的所有点，当前位于 \(l/r\) 时的最小时间。这个状态是平方级别的，很难优化。

观察整个移动过程，发现贡献可以拆成从 \(k\) 直接往两边走的时间 \(\sum{|x_i - x_k|}\) 和在 \(k\) 的两边来回移动的时间。

分析向左边走，对于从点 \(k\) 走到点 \(i\) 时，改变方向去了右边的点 \(j\)，再走回来，这时点 \(j\) 对于前 \(i - 1\) 个点的额外贡献为 \({2(x_j - x_i)} \times {(i-1)}\)，因为到前 \(i - 1\) 个点的时间都增加了 \(2(x_j - x_i)\)。向右走同理。费用提前计算的思想？

不妨让 \(f_i({i} \le {k})\) 表示当前走到点 \(i\) 产生的额外贡献之和的最小值，\(g_i({i} \ge {k})\) 表示当前走到点 \(i\) 产生的额外贡献之和的最小值，得到转移：

转移到 \(i\) 时，对 \((j,n]\) 的点都额外贡献了 \(2(x_j - x_i)\)：

\[f_i = \min \limits_{{j} \ge {k}} {g_j + {2(x_j - x_i)} \times {(n - j)}} \]

转移到 \(i\) 时，对 \([1,j)\) 的点都额外贡献了 \(2(x_i - x_j)\)：

\[g_i = \min \limits_{{j} \le {k}} {f_j + {2(x_i - x_j)} \times {(j - 1)}} \]

其实转移状态的过程可以理解为找转折点（改变方向）的最优选择方案。

最终的最小时间为 \(\min{\{f_1,g_n\}} + \sum{|x_i - x_k|}\)。

但是发现转移有环且顺序不定，把转移看成正权无向图上的边，依照最短路的思想可以 dijkstra，从最小的点开始转移，考虑完 \([l,r]\) 后再选择 \(l - 1\) 和 \(r + 1\) 中更小的转移。

直接转移是 \(O(n ^ 2)\) 的，拆开转移式发现可以用斜率优化，上李超线段树维护即可，时间复杂度为 \(O(n\log^2{n})\)。

也可以把状态转化成凸包，\(O(n)\) 维护凸包，不过更麻烦？

09/17

在宿舍偶遇到很有感觉的大雨，幸运当时在丢瓶子，并未洗澡，得以获得在宿舍走廊玩雨的机会（真的很爽啊qwq）

后续：晚上开始喉咙痛...

第二天下午去医院看病了...

09/16 ∼ 09/19

初赛复习

09/20

CSP-2025-S1 比赛日

考点在石门实验学校，我是跟学校租的大巴一起出发和返回的。

上午补了一道模拟赛的题，浅浅看了一下初赛复习的笔记；

中午吃了顿面，回机房看已经结束的 J1 试题，最后一道题考法很新颖，于是尝试了一下。

\(13:00\) 上大巴出发，大概 \(13:30\) 到的，然后就故地重游，感慨了一下小学部的设施，和我以前的初中部完全就不是一个样的，剩下大部分时间在明德楼楼下闲聊。

\(14:00\) 可以去考场了，有幸体验了石实的新教室，就是不一样哈。

\(14:30\) 准时开考，并没有提前做完，最后五分钟才作答和检查完毕。

关于考题，我压中了一道主定理，这个是我备赛第一天就笃定会考的，直觉还是不错的。

\(16:30\) 结束考试，然后天气不怎么好，下大雨，导致本来预定的 \(16:40\) 返程一直拖到了 \(17:30\)，中间经历了什么找车啊的小事，走了两次反方向的路，最终上车前鞋里已经全是水了，也是历经 \(2h\) 的湿鞋回到家。

在车上讨论了一会儿，已经知道自己错了几道题，只剩 \(89'\) 了，预估自己 \([85',89']\)，痛惜没认真去理解最后一个完善程序题（考场上是靠感觉做的），不然应该更高的。

上小图灵估分，一开始是 \(87'\)，但是我觉得有一道题小图灵错了，后面小图灵又改了，变成了 \(89'\)。

预期：\(89\) pts

\(09/25\) upd：\(89\) pts

09/22

T1 AT_abc302_g [ABC302G] Sort from 1 to 4

题意

给定一个长度为 \(n\) 的序列 \(a\)，\({a_i} \in {[1,4]}\)，可以任意交换位置，求使得序列 \(a\) 变成单调不减序列的最小交换次数。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}}\)

Solution

很容易能想到让 \(a_i\) 向其属于的位置连边，不妨将整个序列划分成 \(4\) 个区间，\(cnt_{i,j}\) 表示 \(i\) 区间的数向 \(j\) 区间连边的个数。

接着一个很简单的性质，连边后必然会构成若干个环，且每个环的大小 \(\le {4}\)；一个大小为 \(m\) 的环的贡献为 \(m - 1\)，最小化交换次数，其实就是最大化环的个数。

然后就能想到依次找大小为 \(2,3,4\) 的环，记录贡献即可。

T2 P11338 [COI 2019] LJEPOTICA

没怎么学过数位 dp，于是趁着台风假补学了一下。

引用当天发的犇犇：

当你放弃记忆化搜索而选用最淳朴的方法去做多状态的数位dp，你将会达成“惊人的注意力”成就

题意

有一个深度为 \(n\) 的完全二叉树，从根节点 \(1\) 出发，给定一条包含 L,R 的路径 \(s\)，分别表示向左右儿子移动，每次移动前都可以改变方向（初始方向是不定的），移动过程中恰好改变了 \(k\) 次方向，求问所有可能移动到的值域在 \([A,B]\) 之间的节点的权值和。

\({2} \le {n} \le {{10} ^ {3}},{0} \le {k} \le {n-1}\)

Solution

很套路的数位 dp 计数题，把 \([A,B]\) 拆成 \([1,B] - [1,A - 1]\)。

注意，由于初始方向是不定的，要分别算出初始方向为左右的贡献。

每一步的贡献可能为 \(\times {2}\) 或者是 \(\times {2} + 1\)，发现暴力计算贡献非常复杂，不妨把 \(\times {2}\) 和 \(+ 1\) 分开计算，于是：

\(f_{i,j,0/1,0/1}\) 表示移动到第 \(i\) 层，改变了 \(j\) 次方向，是否按照初始的方向走，是否顶到上界的总贡献；

\(g_{i,j,0/1,0/1}\) 表示第 \(i\) 层中符合上述条件的数的个数。

转移方程式是好推的，太多了不作分析，时间复杂度为 \(O(n ^ 2)\)。

其实可以用记忆化搜索？太难理解了，不想打导致的qwq

Reflect

在考场上有一直想着怎么搞定怎么结合 \(\times {2}\) 和 \(\times {2} + 1\)，但是直接做太多太复杂了，其实可以尝试想拆开计数，再合并贡献。

T3 P12430 [BalticOI 2025] Exponents

同样的拜谢 @Lgx_Q 大佬的做法。和题解区其他做法都不一样的独特优美做法。

题意

定义 \(a\) 和 \(b\) 的合并为 \(a + b = \max{\{a,b\}} + 1\)。

给定一个长度为 \(n\) 序列 \(a\)，\(q\) 次询问 \((s,t)\)，对序列 \(a\) 中区间 \([s,t]\) 的任意相邻两个数合并，求合并到最后一个数时的最小值，每次询问之间相互独立。

\({1} \le {n,q} \le {{3} \times {{10} ^ {5}}},{0} \le {a_i} \le {{10} ^ {6}}\)

Solution

显然的，从最小的数开始合并必然是最优的，所以先考虑权值最小的连续段，设其长度为 \(L\)，权值为 \(x\)，先讨论每个数至多合并一次的情况，合并后所有数都满足 \(\le {x + 1}\)，若使其长度尽可能小，则以后合并的次数就变少，最终的值也就更小，那么就令相邻数两两配对，新的长度为 \(\lfloor {\frac{L}{2}} \rfloor\)。

由上可以推出：把连续段中所有数变成 \(\le y\) 时的最小长度，就是 \(\large {\lfloor {\frac{L}{{2} ^ {y - x}}} \rfloor}\)。

令 \(f(x) = \lfloor {\frac{x}{2}} \rfloor\)，记 \(y\) 次复合为 \(f^{y}(x) = f(f^{y-1}(x)),{y} \ge {2}\)，要证明：\(f^{y}(x) = \lfloor {\frac{x}{{2} ^ {y}}} \rfloor\)：

引理：对于任意整数 \(n\) 和正整数 \(m\)，有 \(\lfloor {\frac{\lfloor {\frac{n}{m}} \rfloor}{k}} \rfloor = {\lfloor {\frac{n}{mk}} \rfloor}\)。
- 证明；设 \(n = mq + r,{0} \le {r} < {m}\)，则 \(\lfloor {\frac{n}{m}} \rfloor = q\)；
  再设 \(q = ks + t,{0} \le {t} < k\)，则 \(\lfloor {\frac{q}{k}} \rfloor = s\);
  于是有 \(n = m(ks + t) + r = mks + mt +r\)。
  由于 \({mt + r} < {mt + m} \le {m(t + 1)} \le {mk}\)，所以 \({mt + r} < {mk}\)；因此 \(\lfloor {\frac{n}{mk}} \rfloor = s = \lfloor {\frac{\lfloor {\frac{n}{m}} \rfloor}{k}} \rfloor\)，证毕。
用归纳法证明。当 \(y = 1\) 时，显然成立：\(f(x) = \lfloor {\frac{x}{2}} \rfloor = \lfloor {\frac{x}{{2} ^ {1}}} \rfloor\)。
假设对某个 \({y} \ge {1}\) 有 \(f^{y}(x) = \lfloor {\frac{x}{{2} ^ {y}}} \rfloor\)，那么 \(f^{y+1}(x) = f(f^{y}(x)) = \lfloor {\frac{f^{y}(x)}{2}} \rfloor = \lfloor {\frac{\lfloor {\frac{x}{{2} ^ {y}}} \rfloor}{2}} \rfloor\)；
令 \(n = x,m = {2} ^ {y},k = 2\)，由引理可得 \(f^{y+1}(x) = \lfloor {\frac{x}{{2} ^ {y+1}}} \rfloor\)。
由数学归纳法，对任意正整数 \(y\)，有 \(f^{y}(x) = \lfloor {\frac{x}{{2} ^ {y}}} \rfloor\)，证毕。

模拟一下过程，其实就是权值小的连续段向上往权值大的连续段合并；顺着思路，对全局从大到小建立出来一个广义笛卡尔树状物，对于树上的点 \(u\)，值域区间为 \([l_u,r_u]\)，设 \(f_u\) 表示对原序列中的区间 \([l_u,r_u]\) 进行合并后得到的新序列 \(b\) 满足 \(\forall {i},{b_i} \le {a_u}\) 时的最小长度；由树的底部向上转移。

令 \(ls,rs\) 为 \(u\) 的左右儿子，那么容易得到转移式为：

\[f_{u} = \frac{f_{ls}}{{2} ^ {a_u - a_{ls}}} + \frac{f_{rs}}{{2} ^ {a_u - a_{rs}}} + 1 \]

考虑将询问 \((s,t)\) 挂在笛卡尔树的 \(z = lca(s,t)\) 上，转移到 \(z\) 时再处理询问。

一个小 trick：当询问 \((l,r)\) 支持离线且在分治、笛卡尔树等具备树分支结构上操作时，可以尝试维护贡献的前后缀。

改定义为 \(f_{u} = f_{l_u,r_u}\)，以点 \(u\) 为分界线维护前缀 \(g_i = f_{i,u - 1}\) 和后缀 \(h_j = f_{u+1,j},{u+1}\)。挂在点 \(u\) 上的区间 \([s,t]\) 合并到最后一个数的最小值就是 \(a_u + \lceil {\log_2{(g_s + h_t + 1)}} \rceil\)。

维护前缀 \(g\) 和后缀 \(h\) 可以用线段树实现，对区间作向下整除运算（注意特判除以 \(1\) 的情况，此时不需要操作）；线段树维护区间最大值 \(mx\)，最小值 \(mn\)，除数 tag \(k1\)，是否被覆盖 tag \(k2\)；对于一段区间，若 \(\lfloor {\frac{mx}{k1}} \rfloor = \lfloor {\frac{mn}{k1}} \rfloor = v\)，则说明这个区间当前操作完后数值都为 \(v \to {k2}\)，直接覆盖即可。

由势能分析，每个数最多被除 \(O(\log{V})\) 次，所以时间复杂度为 \(O(n(\log{n}+\log{V}))\)。

T4 P9536 [YsOI2023] Prüfer 序列*

09/23

“桦加沙”台风，最低达到 900.3 百帕了？因此，佛山竟然放了两天台风假，记得上一次还是小学时的“山竹”台风。

昨天晚上不是说肯定不放假的吗？？？

09/24

台风在登陆向西折了，对珠三角的影响不大，我甚至都感觉没来过。

放假了，台风又过来应付一下，最好的结果？其实周末要补课...

09/25

出初赛分数了。

2025CSP-S1

S 组的保护分数线是 \(62.5'\)，预料之中？

怎么又考一套模拟赛，上一套都还没补完呢；zsq 说以后一周三套模拟赛，如何呢。

T1 AT_abc307_f [ABC307F] Virus 2~

题意

给定一张 \(n\) 个白点 \(m\) 条边 \((u_i,v_i,w_i)\) 的有权无向图，第 \(0\) 时刻，有 \(k\) 个点被染成了黑色。

有 \(d\) 个时刻，在第 \(i\) 时刻时，若点 \(j\) 被染成黑色的条件：

与任意一个被染成黑色的点最短距离 \(\le {X_i}\)。

问每个点被染成黑色的最早时间，若无法被染成黑色，则输出 -1。

\({1} \le {k} \le {n} \le {{3} \times {{10} ^ {5}}},{0} \le {m} \le {{3} \times {{10} ^ {5}}},{1} \le {d} \le {{3} \times {{10} ^ {5}}}\)

\({1} \le {u_i,v_i} \le {n},{1} \le {w_i,X_i} \le {{10} ^ {9}}\)

Solution

实质是对图跑多源最短路，问题在于如果在第 \(i\) 时刻对所有黑点的边都进行遍历，复杂度为平方级别。

考虑用小根堆维护黑点与白点之间的连边，对于第 \(i\) 时刻，直接从 \(\le {X_i}\) 的边开始做多源最短路，用堆维护最大的剩余距离 \(x_u\)，遍历 \(u\) 的连边 \((w_{u,v},v)\)：

若 \({w_{u,v}} \le {x_u}\)，则说明第 \(i\) 时刻初始的黑点能够到达点 \(v\)，且 \(x_v = x_u - w_{u,v}\)；
若 \({w_{u,v}} > {x_u}\)，则说明还无法将点 \(v\) 染成黑色，将 \((w_{u,v},v)\) 加入小根堆中。

每条边都只会被遍历一次，均摊下来是 \(O(n)\) 级别的（\(n,m\) 视为同阶）。

总时间复杂度为 \(O(n\log{n})\)，瓶颈在堆维护连边和最短路，把这种做法称为双堆做法。

Reflect

接下来讲一下另一种做法（也是考场上的雏形思路，顺便反思）。

定义每个点最后在第 \(d_i\) 天被染成黑色。

一开始是想着对 \(X_i\) 前缀和 \(s_i\)，然后跑多源最短路，再对每个点的 \(dis_i\) 进行二分答案；

接着发现对于每个点，在第 \(d_i\) 天被染成黑色时需要的路程不一定是原图的最短路；

尝试在做多源最短路时二分答案 \(d_i\)，并把 \(s_i \to dis_i\)，这样就处理掉了上面的问题；

紧接着随着而来的又一个问题，对于点 \(i\) 的邻点 \(j\) 来说，可能满足 \(d_i = d_j\)，按照上面的更新方法无法实现这种情况。

下面的我考场上就没想到了...

其实跟第一种方法的本质的思考点，问题出在 \(dis_i\) 就更新成了 \(s_i\)，那不妨改变其定义，每个点的 \(dis_i = (d_i,x_i)\) 表示点 \(i\) 在第 \(d_i\) 天被染成黑色，与其源头的距离为 \(x_i\)，那么转移为：

若 \({x_u + w_{u,v}} \le {X_{d_u}}\)：
- \(dis_v \gets (d_u,x_u + w_{u,v})\)；
反之，则说明点 \(v\) 在第 \(i\) 时刻不能被染成黑色，找到点 \(v\) 被染成黑色的最早时刻 \(i({i} > {d_u})\)，满足 \({w_{u,v}} \le {X_i}\)：
- \(dis_v \gets (i,w_{u,v})\)。

考虑第二种情况的快速转移，求区间 \([d_u + 1,n]\) 中最小的满足条件的 \(i\)，可以用 st 表预处理，也可以用线段树上二分，复杂度为单 log 或者双 log，区别在于具体实现。

T2 P12426 [BalticOI 2025] BOI acronym

题意

有一个由 a,b,c 组成的长度为 \(n\) 字符串 \(S\)，全局的绝对众数是 a。

给定 \(\forall {{1} \le {i} \le {j} \le {n}}\) 的 \(d_{i,j}\)，表示区间 \([l,r]\) 的众数出现的次数（不一定是绝对众数）。

求字符串 \(S\) 中每个 a 出现的位置。

\({1} \le {n} \le {2000}\)

Solution

令 \(m = d_{1,n}\) 表示 a 出现的次数，很显然可以确定最左/右的 a 出现的位置 \(l,r\)。

重要性质：考虑从左到右逐位确定每个数是否是 a。

对于 \(i\)，已经确定了 \([l,i)\) 中 a 的个数为 \(x\)，分类讨论 \([l,i)\) 和 \([i,r]\) 中是否存在某一段区间满足 a 是绝对众数：

\([l,i)\) 的前提条件是满足 a 是区间的众数 \(d_{l,i-1} = x\) 且判定是绝对众数 \(d_{l+1,i-1} = x - 1\)：
- 若 \(d_{l,i} = x + 1\)，则说明 \(i\) 位置上是 a；否则位置 \(i\) 必然不为 a。
\([i,r]\) 的前提条件是满足 a 是区间的众数 \(d_{i,r} = m - x\) 且判定是绝对众数 \(d_{i,r-1} = m - x - 1\)：
- 若 \(d_{i+1,r} = m - x - 1\)，则说明 \(i\) 位置上是 a；否则位置 \(i\) 必然不为 a。
\([l,i)\) 和 \([i,r]\) 的绝对众数都不是 a，则 b,c 一定分别是两边的众数（不一定为绝对众数，可能和 a 的数量相同），由于 a 是 \([1,n]\) 的绝对众数，所以字母 b/c 不可能同时成为两边的众数：
- 不妨取 \((l,i)\) 和 \([i,r)\)，分别舍去了一个 a，那么 b,c 分别是这两段区间的绝对众数，假设 \((l,i),[i,r)\) 的绝对众数分别是 b,c：
  - 若 \(d_{l+1,i-1} = d_{l+1,i}\)，则说明第 \(i\) 位不是 b；
  - 若 \(d_{i,r-1} = d_{i+1,r-1}\)，则说明第 \(i\) 位不是 c。
- 综上所述，若同时满足 \(d_{l+1,i-1} = d_{l+1,i}\) 且 \(d_{i,r-1} = d_{i+1,r-1}\)，则第 \(i\) 位是 a。

这部分是线性的，总时间复杂度为 \(O(n^2)\)，瓶颈在输入qwq。

Reflect

在 \([l,i)\) 和 \([i,r]\) 中存在某一段区间满足 a 是绝对众数时，不能用 \(d_{l+1,i} = x\) 或 \(d_{i+1,r-1} = m - x - 2\) 去判定第 \(i\) 位是否为 a，因为不能保证区间 \([l+1,i-1]\) 和 \([i,r-1]\) 的绝对众数是 a（我们只推出了 \([l,i)\) 或 \([i,r]\) 的绝对众数是 a，要想清楚，依据已有条件来拖判定式）。

T3 P12558 [UOI 2024] Heroes and Monsters*

T4 [Baekjoon 21096] Binary Search Tree*

09/27

T1 CF1984D "a" String Problem

题意

给定一个仅包含小写字母的字符串 \(s\)，求满足以下条件的子串 \(t\) 的个数：

\(t \ne \text{a}\)；
\(s\) 可以由若干个 \(t\) 和若干个 \(\text{a}\) 组成；
组成 \(s\) 的子串中至少有一个 \(t\)。

\({2} \le {|s|} \le {{2} \times {{10} ^ {5}}}\)

Solution

很容易想到分类计数：

\(1\) 类子串：以 \(\text{a}\) 作为 \(t\) 的开头；
\(2\) 类子串：以其他字符作为 \(t\) 的开头。

显然 \(2\) 类子串的计数更加容易想，因为要保证 \(s\) 中不为 \(\text{a}\) 的位置都被覆盖到，且这样的 \(t\) 的开头必然是第一个不为 \(\text{a}\) 的字母 \(s_p\)；

枚举 \(2\) 类子串 \(t\) 的长度 \(i\)，那么 \(s_{[p,p+i-1]}\) 就是 \(t\)，然后向后跳判定这个子串 \(t\) 是否满足条件，找到 \(s_{(p+i-1,n]}\) 中第一个不为 \(\text{a}\) 的位置 \(x\)，查找可以预处理，判断 \(s_{[x,x+i-1]}\) 是否为 \(t\)：

若为 \(t\)，则继续跳，直至不能跳为止，如果最后 \(s_{[x,n]}\) 中的字符都为 \(\text{a}\)，说明这个 \(t\) 是满足条件的子串之一；
否则说明这个 \(t\) 不满足条件，舍去。

接下来考虑怎么处理 \(1\) 类子串，发现一个关键性质：\(1\) 类子串中必然包含满足条件的 \(2\) 类子串。

那么就可以在找到满足条件的 \(2\) 类子串 \(t\) 时加以计算，将该子串 \(t\) 在 \(s\) 中的起始位置 \(x\) 都记录下来，只需要取相邻两个 \(t\) 之间的 \(\text{a}\) 的个数的最小值 \(m\)，即 \(1\) 类子串的贡献；再加上 \(1\) 个 \(2\) 类子串的贡献即可。区间 \(\text{a}\) 的个数可以用前缀和维护。

由调和级数可以知道时间复杂度是 \(O(n\log{n})\) 的。

Reflect

要想完全想清楚怎么打了再去打代码，不然边打边想效率很低；还有不要乱加特判，计数时要仔细一点，想的要周到些。

T2 P11352 [NOISG 2024 Finals] Coin

题意

有 \(n\) 个不同的硬币，称重 \(m\) 次，第 \(i\) 次称重 \((x_i,y_i)\) 表示 \(x_i\) 比 \(y_i\) 轻。

找出每个硬币首次确定排名的称量序号，或者判断这个硬币的排名永远无法确定。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}},{1} \le {m} \le {{8} \times {{10} ^ {5}}}\)

Solution

很容易想到让 \(x_i\) 向 \(y_i\) 连边，其实就是在 \(n\) 个点 \(m\) 条边的 DAG 上对每个点 \(u\) 求最小的 \(i\) 使得保留 \(i\) 条边后点 \(u\) 的拓扑序唯一（通俗点讲就是 \(\forall {v \ne u}\)，都有 \({u} \to {v}\) 或 \({v} \to {u}\) 的路径）。

考虑对 DAG 做拓扑排序，显然点 \(u\) 能被确定需要满足：

点 \(u\) 出队列时，队列为空（若还有节点 \(v\) 在队列中，无法比较 \(u\) 和 \(v\) 的大小，也就不能确定点 \(u\) 的排名）；
可以由当前节点到达剩下还未入队列的点。

先想第二个条件，思考一个性质：对于 DAG 上的保留每个点的一条入边，不影响连通性。

由此对于每个点，只需要维护 未被遍历的入边 中出现的时间最小的那条边，求这些边的最大值即可，可以用 set 或优先队列实现。

对 DAG 正反做两次拓扑排序，记在正反拓扑到点 \(u\) 时未被遍历的点的数量分别为 \(s,t\)，若 \(s + t = n - 1\)，则点 \(u\) 必然能被确定；反之不能。

时间复杂度为 \(O(n\log{n})\)，瓶颈在于 set 或优先队列（可能优先队列会更快？）的维护；空间复杂度为 \(O(n)\)。

T3 [Baekjoon 18760] Heavy Stones*

T4 CF1975D Paint the Tree

前文讲过qwq

09/30

2025.09 每月回顾题目

这个月任务量太大了，没怎么顾及这个记录，才写了两题，下个月尽量写吧...

就一直等着放假，期间和超强的 lyl 猜城市。

晚上抢十一国庆的广东博物馆票，运气好抢到了。

国庆八天假，放三天，国庆一号二号，六号中秋，呜呜呜。

10/01

去广东省博物馆咯。

10/03

不要回校集训啊啊啊！！！

今天的后两题是给人做的吗。

T1 CF1942C2 Bessie's Birthday Cake (Hard Version)

题意

有一个正 \(n\) 边形，顶点从 \(1\) 到 \(n\) 顺时针编号，有 \(x\) 个关键点 \(a_i\)，至多再选 \(y\) 个关键点，在关键点之间连边，边不相交，最大化切出的三角形个数。

\({4} \le {n} \le {10} ^ {9},{2} \le {x} \le {\min\{n, {2} \times {{10} ^ {5}} \}},0 \leq y \leq n - x\)

Solution

先将已知的关键点互相连边，一个 \(m\) 边形最多被切出 \(m - 2\) 个三角形，解法之一就是对一个点向除了相邻的点外的 \(n-3\) 个点分别连边，构成 \(n - 2\) 个三角形，初始化 \({cnt} \gets {n - 2}\)。

考虑在两个相邻的关键点之间选点连边，比较优的选法肯定是隔多个点选一个，贡献为 \(2\)，因为会多出来一条相邻的边；若同时选择两个相邻的点，贡献为 \(1\)，更劣。

由于间隔数的大小与贡献没有关系，\(y\) 足够的情况下，为了贡献最大化，就需要更多的关键点，所以最优的选法就是隔一个点选一个。

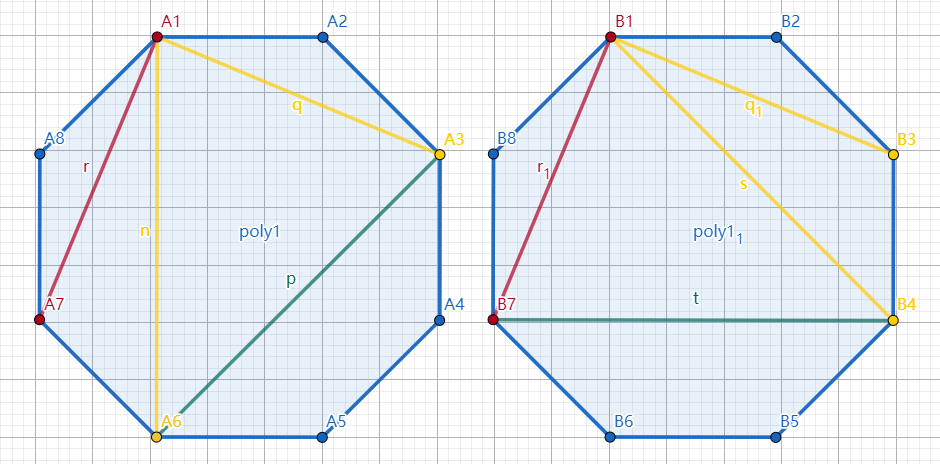
如下图，两个红点为初始的关键点，黄点为选择的关键点，以 \(A_1\) 为源点，向 \(A_3,A_5\) 连边（黄边），\(A_3,A_5,A_7\) 相邻点之间再互相连边（绿边）， \(A_1\) 到 \(A_7\) 之间贡献的三角形个数为 \(5\)：

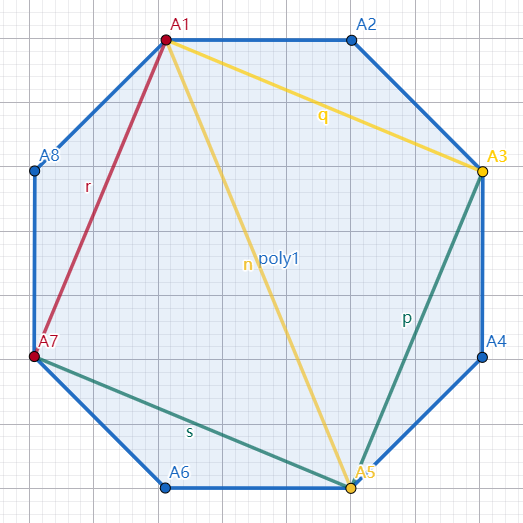
CF1942C2_1

在选同样多的点的前提下，下面两种选法更劣，\(A_1\) 到 \(A_7\) 之间贡献的三角形个数为 \(4\)：

CF1942C2_2

最后对初始相邻两个关键点的间隔数按奇偶数分类讨论计算贡献即可，注意对 \(y\) 限制的细节处理。

时间复杂度为 \(O(x\log{x})\)。

Reflect

隔一个选一个还是容易想到的，计算贡献时思路混乱了，想把初始和选择的关键点拿出来一起算，这样就必须要找出一个源点，很复杂...

以后可以在计算贡献多往子问题算再加起来想。

T2 P9737 [COCI 2022/2023 #2] Lampice

题意

在 \({(n+1)} \times {(m+1)}\) 的矩阵上有 \(k\) 种不同的数字各两个，求满足以下条件的子矩阵数量：

长宽均 \(\ge {2}\)；
对于每种数字，要么都在子矩阵内，要么都在其外。

\({1} \le {n} \le {150}，{1} \le {m} \le {1000},{0} \le {k} \le {{2} \times {{10} ^ {5}}}\)

Solution

很明显的异或哈希（和哈希也可以），用随机哈希值（可以用自然溢出 unsigned long long），赋给同种数字的两个位置，对子矩阵做矩阵异或和 \(S\)，若 \(S = 0\)，则子矩阵满足条件。很套路：

枚举子矩阵 \((i,l,j,r)\) 的 \(i,j\)，再枚举列 \(r\)，对矩阵 \((i,1,j,r)\) 维护二维前缀异或和 \(s_{r}\)，找到使得 \(s_l = s_r\) 的 \({l} \le {r}\) 的个数，这个可以用 unordered_map 利用 \(O(1)\) 查询实现。

时间复杂度为 \(O(n ^ 3)\)。

Reflect

一开始想着用扫描线 + 并查集实现？？？后面被 Lindone 大佬点破，题目只要求两个点，而我的并查集维护的是矩阵...

以后遇到判定子矩阵的数量可以往哈希上想，还有记住常用的套路：\(O(n ^ 3)\) 维护前缀和的方法，接着利用单调栈或 unorder_map 等计数。

T3 P7830 [CCO 2021] Through Another Maze Darkly*

T4 P11947 [KTSC 2025] 可爱区间 / maxsum*

10/04

T1 AT_abc304_f [ABC304F] Shift Table

题意

给定一个长度为 \(n\) 的 0/1 字符串 \(s\)，表示 A 在第 \(i\) 天是否工作的工作表。

确定 B 的工作表 \(t\)，对于 \(m\) 满足 \(m | n\)，规划前 \(m\) 天是否工作，第 \(i + m\) 天的工作情况和第 \(i\) 天一样。

求满足每天至少有一个人在工作的 B 的工作表的个数。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}}\)

Solution

枚举 \(n\) 的因数 \(m\)，预处理后 \(O(\sqrt{n})\) 是 \(d(n)\) 的宽松上界。

若 A 在第 \(i\) 天不工作，则 B 在第 \(i\) 天必须要工作，那么第 \(j\) 天满足 \({{j} \equiv {i}} \pmod {m}\) 就都要工作，令 \(f_{{i} \bmod {m}} = 1\)。

对于 \(m\) 来说，设 \({i} \le {m}\) 中 \(f_{i} = 0\) 的个数为 \(x\)，符合条件的工作表的个数为 \({{2} ^ {x}}\)；

但显然不同的 \(m\) 的工作表集合可能会有交集，考虑容斥思想，发现若有 \(m_1 | m_2\)，那么 \(m_2\) 的方案必然包含 \(m_1\)，减去即可。

由上面的思想，\(m\) 的贡献为：

\[g_m = {{2} ^ {x}} - {\sum_{k | m} g_k} \]

对于 \(\sum_{k | m} g_k\) 的处理方法有很多，设 \(p_i\) 表示满足 \(j | i\) 的 \(g_j\) 的和，在计算完 \(k\) 的贡献时，对 \(k | y\) 记录 \({p_y} \gets {p_y + g_k}\)，那么 \(g_m = {{2} ^ {x}} - p_m\)。

时间复杂度为 \(O({n} \times {d(n)})\)。

Reflect

想到了容斥，但是脑筋一直板板地去想“至少”的容斥计数。

要发现 \(m\) 的因子和 \(m\) 有交集！！！

以后遇到容斥可以考虑思考 \(m\) 与因子之间的关系。

T2 P3590 [POI 2015 R2] 三座塔 Three towers/P12765 [POI 2018 R3] 三座塔 2 Three towers 2^

Solution

真的很智慧啊qwq

发现有结论：

最终答案一定要么左端点在 \({l} \in {[1,3]}\)，要么右端点在 \([n-2,n]\)。

（证明有时间再回来补）

Reflect

多猜结论。

T3 P11346 [KTSC 2023 R2] 会议室 2*

T4 [Baekjoon 21089] Excluded Min*

10/05

T1 P9975 [USACO23DEC] Cowntact Tracing 2 B

题意

有一排 \(n\) 头奶牛，第 \(0\) 天有若干头奶牛被染黑。每天晚上，已经被染成黑色的奶牛左右相邻两头奶牛也会被染成黑色。

给定一个长度为 \(n\) 的 0/1 字符串，表示若干天后每头奶牛是否被染成了黑色，求在第 \(0\) 天时被染成黑色的奶牛的最小数量。

\({1} \le {n} \le {{3} \times {{10} ^ {5}}}\)

Solution

显然的，对于一段连续的 1，使得时间 \(t\) 最长的方法就是只选最中间的那头奶牛；特殊的，左右两边的连续段是选最左/右的奶牛。

容易发现，最小化第 \(0\) 天时被染成黑色的奶牛的数量，天数就要最大化；由于要满足所有连续段，所以取最小值 \(day = \min {t}\)，再贪心每个连续段的最少的奶牛个数即可。

T2 P7831 [CCO 2021] Travelling Merchant

题意

给定一个 \(n\) 个点 \(m\) 条边的有向图，每条边 \((u,v,r,p)\) 分别表示边的起点，终点，通过该边的最小要求 \(r\) 和通过后的增加的值 \(p_i\)。

\(\forall {{i} \in {[1,n]}}\)，求从点 \(i\) 出发，能不停走下去的最小初始值。

\({2} \le {n,m} \le {{2} \times {{10} ^ {3}}}\)

\({1} \le {u,v} \le {n},{0} \le {r,p} \le {{10} ^{9}}\)

保证没有自环但可能有重边。

Solution

考虑最大的 \(r\)，由于 \({p} \le {0}\)，从任意点出发都能不停走下去。

\(f_i\) 表示从点 \(i\) 出发，能不停走下去的最小初始值。

类拓扑排序的思想，先对边按 \(r\) 从大到小排序，每次取出剩下的边中最大 \(r_i\) 的边 \(i\)，显然有 \(f_{u_i} = \min{\{f_{u_i},r_i\}}\)：

若点 \(u_i\) 还有出边，则删掉这条边并保留 \(u_i\)；
若点 \(u_i\) 出度为 \(0\)，则 \(u_i\) 的最小初始值已经确定了，将 \(u_i\) 入队并删掉 \(u_i\)；接下来可能又会出现了新的没有出度的点，那么这些点的最小初始值也将确定。

对于队列中的点 \(v\)，由于已经确定的 \(f_v\)，那么就可以倒推回去更新其他点，\(f_{u_i} = \min{\{f_{u_i},\max{\{r_i,f_{v_i} - p_i\}}\}}\)，这里可以建反图实现。

时间复杂度为 \(O(n\log{n})\)，瓶颈在对边的排序。

Reflect

可以尝试从最坏且可以满足所有点的情况出发思考，倒推回去。

T3 P10067 [CCO 2023] Real Mountains*

T4 P11983 [JOIST 2025] 展览会 3 / Exhibition 3*

10/06

中秋节快乐。

买了新的篮球鞋qwq

10/07

T1 [BZOJ 4927] 第一题/[LOJ 6065] 「2017 山东一轮集训 Day3」第一题

题意

给点 \(n\) 根木棍，长度为 \(a_i\)，求选出 \(6\) 根木棍能拼出一个正方形的方案数。

\({1} \le {n} \le {{5} \times {{10} ^ {3}}},{1} \le {a_i} \le {{10} ^ {7}}\)

Solution

把六个数分成 \(4\) 个集合，有 \(\{1,1,2,2\}\) 和 \(\{1,1,1,3\}\) 两种方案。

对 \(a\) 从小到大排序，\(cnt_i\) 表示长度为 \(i\) 的木棍的个数。

设 \(l\) 是正方形的边长。

考虑方案二：

\(\{l,l,l,3x\}\)
\(\{l,l,l,2x+y\}\)
\(\{l,l,l,x+2y\}\)
\(\{l,l,l,x+y+z\}\)

令 \(x = a_i\)，钦定 \({x} > {y,z}\) 且 \(i\) 是最后一个值为 \(a_i\) 的位置，枚举 \(l = a_j\)，那么上述的四种情况都可以归成一种 \(\{l,l,l,x+(l-x)\}\)，其中 \(l - x\) 为两个数之和；

那不妨设 \(sum_x\) 为 \([1,i)\) 中满足 \(a_j + a_k = x\) 的 \((j,k)\) 的个数，那么贡献为 \({\binom{cnt_{l}}{3}} \times {sum_{l-x}}\)。

考虑方案一：

\(\{l,l,2x,2x\}\)
\(\{l,l,2x,y+z\}\)
\(\{l,l,x+y,x+y\}\)
\(\{l,l,x+y,z+w\}\)

第一种情况，\(l = 2x\)，贡献为 \({\binom{cnt_{x}}{4}} \times {\binom{cnt_l}{2}}\)；

由于 \(2x > y + z\)，所以第二种情况不存在。

其中后三种情况的前提条件为 \(l < 2x\)：

第三种情况，\(x = a_i,l = a_j\)，贡献为 \({\binom{cnt_{x}}{2}} \times {\binom{cnt_{l-x}}{2}}\)；

第四种情况，\(x = a_i,l = a_j\)，贡献为 \({{cnt_x} \times {cnt_{l-x}} \times {sum_{l}}}\)。

因为 \(l \le a_n\) 的，所以维护 \(sum\) 时，若 \(a_j + a_k > a_n\)，就不用记录了。

T2 P10299 [CCC 2024 S5] Chocolate Bar Partition~

题意

给定 \({2} \times {n}\) 的矩阵 \(a_{i,j}\)，最大化连通块数量，满足：

每个连通块的平均值相等。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}}\)

Solution

显然的，每个连通块的平均值就是整个矩阵的平均值 \(v\)（处理平均值前可以先对 \({a_{i,j}} \gets {{a_{i,j}} \times {2n}}\)），让 \({a_{i,j}} \gets {a_{i,j} - v}\)，连通块内所有数的和为 \(0\)。

对两行维护前缀和 \(s_{0/1,i}\)，讨论连通块的性质：

对于在一行上的连通块 \((l,r]\)，有 \(s_{i,l} = s_{i,r}\)；
对于跨越两行的连通块，两行的最右侧为 \(r_0,r_1\)，有 \(s_{0,r_0} + s_{1,r_1} = 0\)。

\(f_{i,0/1}\) 表示考虑完前 \(i\) 列的格子，第 \(0/1\) 行的格子所在的连通块的和不保证为 \(0\)。

\(f_{i,k},{k} \in {\{0,1\}}\) 有转移，令 \(l = 1 - k\)（另一行的编号）：

下面的示意图中绿色是已经被划分完了和为 \(0\) 的若干个连通块，黄色是和 不一定 为 \(0\) 的连通块，红色是新划分出来的和一定为 \(0\) 的连通块。

第 \(i\) 列的两个格子并入和不一定为 \(0\) 的连通块内：

\[f_{i,k} = \max{\{f_{i-1,0},f_{i-1,1}\}} \]

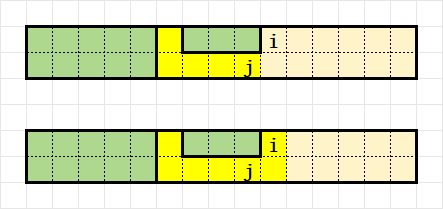
P10299_1

第 \(k\) 行末尾若干个格子单独成为一个和为 \(0\) 的连通块：

\[f_{i,k} = \max_{j < i,s_{j,k} = s_{i,k}}{\{f_{j,k} + 1\}} \]

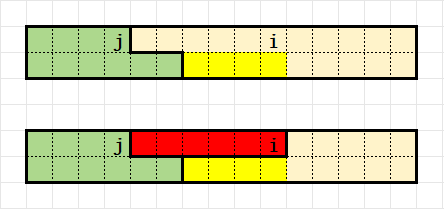
P10299_2

第 \(k\) 行末尾的若干个格子并入跨越两行的和不一定为 \(0\) 的连通块形成一个和为 \(0\) 的连通块；另一行的末尾的格子又产生了一个不一定为 \(0\) 的连通块：

\[f_{i,k} = \max_{j < i,s_{j,l} + s_{i,k} = 0}{\{f_{j,l} + 1\}} \]

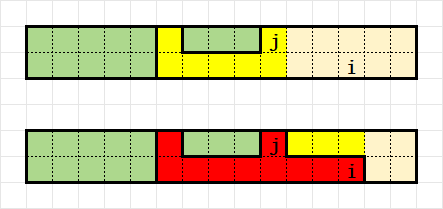
P10299_3

若 \(s_{i,0} + s_{i,1} = 0\)，则此时不保证为 \(0\) 的连通块和为 \(0\)：

\[f_{i,k} = \max{\{f_{i,0},f_{i,1}\} + 1} \]

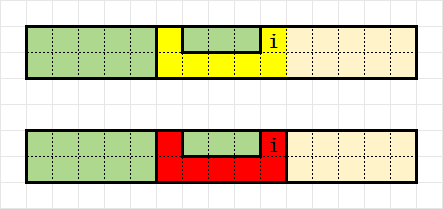
P10299_4

用 unordered_map 维护前缀和能实现 \(O(n)\) 的转移。

T3 P9312 [EGOI 2021] Lanterns / 灯笼*

T4 P5642 人造情感（emotion）*

10/08

T1 AT_arc132_d [ARC132D] Between Two Binary Strings

题意

给定两个由 \(n\) 个 0 和 \(m\) 个 1 组成的字符串 \(s_1,s_2\)。

记 \(f(s_1,s_2)\) 表示每次交换 \(s_1\) 的两个相邻的字符，变成 \(s_2\) 的最小交换次数。

记 \(g(s)\) 表示 \(\sum_{i=1}^{n+m-1}{[s_i = s_{i+1}]}\)，即相邻字符相同的个数。

最大化 \(g(s_3)\)，满足 \(f(s_1,s_2) = f(s_1,s_3) + f(s_3,s_2)\)。

\({0} \le {n,m} \le {{3} \times {{10} ^ {5}}},{n + m} \ge {1}\)

Solution

设 \(p_{i,j}\) 表示 \(s_i\) 中第 \(j\) 个 1 的位置。

根据 \(f(s_1,s_2) = f(s_1,s_3) + f(s_3,s_2)\)，容易得到 \(p_{3,i} \in {[l_i = \min{\{p_{1,i},p_{2,i}\}},r_i = \max{\{p_{1,i},p_{2,i}\}}]}\)，且 1 位置的区间不存在包含关系，对区间 \([l_i,r_i]\) 按 \(l\) 从小到大排序。

接着考虑如何放置能最大化 \(g(s_3)\)，0 的贡献取决于 1 的位置，连续放 1 时，0 的连续段自然也变长，这样的放法必然最优，不妨让 \(p_{3,i}\) 尽量靠右放，使得后面的 1 与其形成连续段。

特殊的，若按照上面靠右放 1 时，发现第一位放 0 可能不是最优的，于是第一个 1 可以选择靠左放。对两种放法取最大值即可。

时间复杂度为 \(O(n\log{n})\)。

T2 P6294 [eJOI 2017] 游戏~

题意

有 \(n\) 个数 \(a_i\)，进行 \(k\) 轮：

给定一个正整数 \({p} \in {[1,n]}\)，\(S\) 为 \({i} \in {[1,p)}\) 的 \(a_i\) 组成的可重集。

依次加入 \(a_i,{i} \in {[p,n]}\)，每加入一个数，A 和 B 轮流取出 \(S\) 中的一个数。

直到 \(S\) 为空，该轮结束。

A 和 B 都希望自己取数的总和最大化，在两人都采用最优策略的情况下，求每轮结束后 A 的取得的数字总和减去 B 取得的数字总和。

\({1} \le {n} \le {{10} ^ {5}},{1} \le {k} \le {{2} \times {{10} ^ {3}}},{k} \le {n}\)

Solution

先模拟每轮的过程，把 \(S\) 中的数全部丢进大根堆中维护，每次取数都取堆顶。

发现对于第 \(x\) 个取数回合，取得的数肯定是当前有的最大的，不妨对 \(a_i\) 从大到小排序，并保留其原来的编号 \(id_i\)，依次处理 \(a_i\)，利用提前占位的思想：

若 \({id_i} \le {p + x -1}\)，则在第 \(x\) 个回合时，\(a_i\) 已经进入了 \(S\) 中，如果 \(a_i\) 已经标记了，则跳过，否则该回合的先手必然选择 \(a_i\)；
反之，提前计算出到 \(a_i\) 会在第 \(y = id_i - p + 1\) 个回合被选择，再对 \(y\) 的奇偶性判断是 A/B 选择的，加入贡献并对其进行标记。

\(k\) 轮的时间复杂度是 \(O(kn)\) 的。

Reflect

对于每轮固定的最优选择方式，可以尝试考虑是否能够提前计算贡献，从而做到优化时间复杂度的效果。

T3 PAT_arc119_f [ARC119F] AtCoder Express 3*

T4 P9058 [Ynoi2004] rpmtdq*

10/09

T1

题意

给定两个整数 \(n,m\)，以及长度为 \(m\) 的取值为 \([1,n)\) 的整数序列 \(x\)。

求是否存在长度为 \(m\) 的一组取值为 \({\{0,1\}}\) 的变量序列 \(a,b\)，满足对于任意长度为 \(n\) 的 01 串 \(s\)，至少存在一个整数 \({i} \in {[1,m]}\) 满足 \(s_{x_i} = a_i \land s_{x_{i + 1}} = b_i\)。

\({2} \le {n} \le {{10} ^ {18}},{1} \le {m} \le {{3} \times {{10} ^ {5}}}\)

Solution

模拟几组数据，记 \(cnt_i\) 为 \(x_j = i\) 的 \(j\) 的个数，可以发现一个结论：

若 \({cnt_{l} \le {2}} \land {cnt_{r} \le {2}}\) 且 \(\forall {{i} \in {(l,r]}},{cnt_i} \ne {0}\)，那么就一定有解。

证明：

可以在至少 \((l,l+1)\) 上放 \(\{(0,0),(1,0)\}\)，\((r,r+1)\) 上放 \(\{(0,0),(0,1)\}\)；若 \(s_{l+1}\) 为 \(0\)，则两个之中必有一个能满足条件；否则可以确定 \(s_{l+1}\) 为 \(1\)。同理可知 \(s_{r}\) 也会被确定。

接下来的每个位置只需要 \({cnt_i} \le {1}\) 就可以依次确定每一位，若满足 \(\forall {{i} \in {(l,r]}},{cnt_i} \ne {0}\)，则会形成闭环，必然有位置 \((x,x+1)\) 被确定。

用前缀和维护一下判定即可，时间复杂度为 \(O(n)\)。

T2 CF2006C Eri and Expanded Sets

题意

称一个不可重集 \(S\) 是好的，当且仅当通过任意次以下操作后，对于 \(S\) 中任意两个元素 \(x,y({x} < {y})\)，对于整数 \(i\) 满足 \({i} \in {[x,y]}\) 都在集合中：

取出集合中的两个元素 \(x,y\)，若 \(\frac{x + y}{2}\) 是整数且不在集合中，将其加入集合。

给定一个长度为 \(n\) 的正整数序列 \(a\)，求区间 \([l,r]\) 满足：

由 \(a_i,{i} \in {[l,r]}\) 组成的不可重集是好的。

\({1} \le {n} \le {{4} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}}\)

Solution

考虑对一个集合 \(S\) 进行扩展得到 \(S'\)：

\(S'\) 的所有元素在 \([\min{\{S\}},\max{\{S\}}]\)。
- 显然的。
\(S'\) 排序后是等差数列。
- 反证法。若不是等差数列，设存在三个相邻的数 \(x,y,z\)，记 \(d_1 = y - x,d_2 = z - y\)，\({d_1} \ne {d_2}\)：
  - 若 \(d_1,d_2\) 都为偶数，显然不是最终的状态；
  - 反之，\(d_1,d_2\) 都是奇数，则 \(d_1 + d_2\) 为偶数，\(\frac{x + z}{2} = \frac{d_1 + d_2}{2} \ne y\)，能产生新的数。
\(S'\) 的公差是 \(S\) 相邻两项差分值的 \(\gcd\) 除以 \(2\) 的若干次幂。
- 设 \(S'\) 的公差为 \(d\)，\(l = \min{\{S\}}\)。\(\forall {{i} \in {S}},{i = l + kd}\)。\(d\) 一定为所有差分值的因数，即所有相邻两数差分值的 \(\gcd\) 的因数。
- 反证，若 \(d\) 中含有因数 \(2\)，则有 \(x,y\) 可以生成 \(\frac{x + y}{2}\)。
\(S'\) 的公差是奇数。
- 若为偶数，则相邻两数可以继续生成新的数。
若 \(S\) 相邻两项差分值的 \(\gcd\) 是 \(g\)，则 \(S'\) 的公差为 \(\frac{g}{\text{lowbit}(g)}\)。
- 由上述性质 \(3\) 得到 \(g = {{d}} \times {{2} ^ {x}},{d,x} \in {\mathbb{N}}\)，其中 \({d}\) 不能被 \(2\) 整除；
- 由于 \({d} \in {\mathbb{N}}\)，所以 \(\text{lowbit}(g) = {{2} ^ {x}}\)，因此得到 \(d = \frac{g}{\text{lowbit}(g)}\)。

当 \(S'\) 是好的，则 \(d = 1\)，相当于找区间 \([l,r]\) 满足区间的 \(\gcd\) 为 \({2} ^ {x}\) 或 \(0\)。

端点具有单调性，可以用 st 表 + 二分维护实现，两只 \(\log\)。

听说可以用 baka's trick？？？没学过qwq

T3 AT_arc178_d [ARC178D] Delete Range Mex

题意

给定一个正整数 \(n\) 和一个长度为 \(m\) 的非负整数序列 \(a\)，\(\forall {{a_i} \in {[0,n)},{i} \in {[1,m]}}\) 且序列中的元素互不相同。

满足以下条件，值域为 \([0,n)\) 的排列 \(b\) 的个数：

可以通过任意次数以下操作将 \(b\) 变为 \(a\)：
- 选择满足 \({1} \le {l} \le {r} \le {|b|}\) 的 \(l,r\)，设序列 \(b\) 的区间 \([l,r]\) 中的元素组成集合 \(S\)，如果 \(\mathrm{mex}(S)\) 在 \(b\) 中出现，则将其从 \(b\) 中删除。

\(\mathrm{mex}(X)\) 的定义如下：对于由非负整数组成的有限集合 \(X\)，\(\mathrm{mex}(X)\) 是满足 \(x\notin X\) 的最小非负整数 \(x\)。

\({1} \le {m} \le {n} \le {500}\)

Solution

发现 \(x\) 能被删除，前提条件是选择的子区间 \([l,r]\) 包含 \([0,x)\) 中的所有元素并且不包含 \(x\)。

若 \(x\) 在删除序列中，则小于 \(x\) 的数都在 \(x\) 的左/右边，且删掉 \(x\) 时，小于 \(x\) 的数都还存在。删数的顺序是从大到小的。

倒着来，考虑从小到大插入数字，每个位置左右两边一个空隙（妙啊，理解一下，相当于空隙上放删除序列中的数，原本的位置上放需要保留下来的数），序列长度为 \(m\)，故有 \(m + 1\) 个空隙可以插入，同一个空隙可能插入多个数字，记 \(p_i\) 表示 \(i\) 在序列 \(a\) 中出现的位置。

区间 dp，\(f_{l,r,k}\) 表示当前已确定插入 \([0,k]\)，且后续的填数空隙编号 \(\le {l}\) 或 \(\ge {r}\) （可以理解为第 \(l\) 个空隙到第 \(r\) 个空隙之间维护的位置 \(i \in {(l,r)}\) 已经满足 \(b_i = a_i\)）的方案数，有转移：

如果 \(x\) 已经在序列 \(a\) 中出现过，则其位于 \([p_x,p_x + 1]\) 的空隙之间：\({f_{l,r,x}} \gets {f_{\min{\{p_x,l\}},\max{\{p_x+1,r\}},x}}\)。
如果没有在序列 \(a\) 中出现过，则说明 \(x\) 在删除序列中：
- 若 \(x\) 插在小于 \(x\) 的数的左侧：\({f_{l,r,x}} \gets {\sum_{i=l}^{r}{f_{i,r,x-1}}}\)；
- 若 \(x\) 插在小于 \(x\) 的数的右侧：\({f_{l,r,x}} \gets {\sum_{i=l}^{r}{f_{l,i,x-1}}}\)。

转移可以在枚举 \(i\) 这一维时用前缀和优化掉。

特别的，考虑 dp 的初始化，\(0\) 比较特殊：

如果序列 \(a\) 中已经出现过 \(0\)：\(f_{p_0,p_0+1,0} = 1\)；
否则，根据性质，任意一个数都能删掉 \(0\)，因此 \(0\) 可以插在任何的位置：\(\forall {{i} \in [1,m+1]},{f_{i,i,0} = 1}\)。

时间复杂度为 \(O(m ^ 2n)\)。

Reflect

若出现类似于本题的删除啊，什么的，要把序列中两种性质的数分开，不妨想一想插空，特别是时间复杂度为平方或者立方的 dp 类型。

T4 AT_arc174_f [ARC174F] Final Stage*

10/10

T1 P9350 [JOI 2023 Final] 宣传 2 / Advertisement 2~

题意

给定 \(n\) 个点，点 \(i\) 有 \((a_i,b_i)\)，最小化关键点数量，使得对于 \(\forall {{i} \in {[1,n]}}\)，至少存在一个 \({j} \in {[1,n]}\)，满足 \(j\) 是关键点且 \({|a_j - a_i|} \le {b_j - b_i}\)。

\({1} \le {n} \le {{5} \times {{10} ^ {5}}},{1} \le {a_i,b_i} \le {{10} ^ {9}}\)

Solution

请记住下面这个神奇的性质。

考虑拆绝对值，分类讨论：

当 \({a_j} > {a_i}\) 时：
- \({{a_j - a_i} \le {b_j - b_i}} \iff {{a_j - b_j} \le {a_i - b_i}}\)
当 \({a_j} < {a_i}\) 时：
- \({{a_i - a_j} \le {b_j - b_i}} \iff {{a_j + b_j} \ge {a_i + b_i}}\)
当 \(a_j = a_i\) 时可以列入上面任意一种情况。

令 \(l_i = a_i - b_i，r_i = a_i + b_i\)，则点 \(i\) 可以到达点 \(j\) 的充要条件为 \({l_j} \le {l_i} \le {r_i} \le {r_j}\)。

那么题目就转化为最小化选择区间满足能覆盖所有区间，对 \((l_i,r_i)\) 排序后贪心选取即可。

时间复杂度为 \(O(n\log{n})\)。

Reflect

上一次遇到类似的题，其实没怎么弄懂这个性质（明明满足一个就可以了，为什么判定的时候可以同时满足），现在明白了。

有一种无效果的推导，放这起警示作用：

当 \({a_j} > {a_i}\) 时：
- \({{a_j - a_i} \le {b_j - b_i}} \iff {{b_j - a_j} \ge {b_i - a_i}}\)
当 \({a_j} < {a_i}\) 时：
- \({{a_i - a_j} \le {b_j - b_i}} \iff {{b_j + a_j} \ge {b_i + a_i}}\)

这时候的 \(l_i = b_i - a_i,r_i = b_i + a_i\)，但是并不具有 \({l_j} \le {l_i} \le {r_i} \le {r_j}\)，只能推出 \({l_i} \le {l_j},{r_i} \le {r_j}\)。

T2 CF1473E Minimum Path~

脑电波题？又让我回想起了那次 CSP-J T4，同样是分层图，上次是不会知识点，这次又没看出来...

题意

给定一个 \(n\) 个点 \(m\) 条边的带权无向连通图。

定义若一条路径所包含的边组成的边集 \(E\)，那么这条路径的权值为 \(\sum \limits_{{i} \in {E}}{w_i - {\max \limits_{{i} \in {E}}{w_i}}} + {\min \limits_{{i} \in {E}}{w_i}}\)。

对于 \(\forall {{i} \in {(1,n]}}\)，求从编号 \(1\) 到编号 \(i\) 的点所有路径权值的最小值。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}}\)

\({1} \le {u_i,v_i} \le {n},{1} \le {w_i} \le {{10} ^ {9}},{u_i} \ne {v_i}\)

Solution

对于一条路径，要求可以转化为：在路径上选择一条边减去其权值，再选择一条边加上其权值，路径的长度的最小值。

可以证明，不合法的选边方案是更劣的，因此最后得到的最小值必然是合法的。

考虑分层图，\(dis_{u,0/1,0/1}\) 表示从点 \(1\) 到点 \(u\) 的路径，是否选择一条边减去了其权值，是否选择一条边加上其权值，路径长度的最小值。

状态也可以变为 \(dis_{u,0/1/2/3}\)，可以用位运算实现，便于转移。

直接跑 dijkstra，注意转移式子的条件判定细节即可，时间复杂度是 \(O(n\log{n})\) 的。

Reflect

看到类似的对一些边/数集合做 \(\max,\min\) 做加减等操作，且满足不合法的选择方案是更劣的时，不一定要钦定选了最大/小的，不妨尝试随便乱选值，只要能使最后求出来的结果是合法的方案中的最优的即可（类比上述解法的第一段的要求转化方法）。

还有对图做最短路，又有条件限制的，可以考虑分层图。

T3 P9020 [USACO23JAN] Mana Collection P*

T4 [QOJ 2378] Tree Permutations*

10/11

无视风险，百万撤离成功，喜提放假。

T1 [UOJ 887] 最酷的排列

题意

给定一个长度为 \(n\) 的序列 \(a\)，可以进行若干次操作：

对区间 \([l,r]\) 从小到大排序。

给定一个长度为 \(n\) 的 01 串 \(b\)，经过若干次操作后，最小化 \(\sum_{i=1} ^ {n}{{a_i}{b_i}}\)。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}},{b_i} \in {\{0,1\}}\)

Solution

很显然有一个性质，如果想使得 \(b_i = 1\) 的位置 \(i\) 上的 \(a_i\) 变小，变小的值只能从后面取。

考虑从后往前扫，用小根堆维护当前还没取的 \(a_i\) 的最小值，遇到一个 \(b_i = 1\)，直接取堆顶的数填上是最优的。

可以尝试用构造来证明：\(\forall {{i} \in {[1,k]}}\) 的 \(x_i\) 满足 \(b_{x_i} = 1\)，最后 \(b_i = 1\) 位置上的 \(a_i\) 的原位置为 \(y_i,{{i} \in {[1,k]}}\)，依次对区间 \([x_i,y_i]\) 排序即可。也可以用提前占坑来感性理解？？？

时间复杂度为 \(O(n\log{n})\)。

T2 CF1628D2 Game on Sum (Hard Version)

题意

初始 \(x = 0\)，进行 \(n\) 个回合：

A 选择一个区间在 \([0,k]\) 的实数 \(t\)。
B 可以选择让 \(x\) 变成 \(x + t\) 或者 \(x - t\)，且 B 在 \(n\) 个回合中至少选择 \(m\) 次让 \({x} \gets {x + t}\)。

A 希望 \(x\) 最大化，B 希望 \(x\) 最小化，双方均采用最优策略，求最后 \(x\) 的值。

\({1} \le {m} \le {n} \le {{10} ^ {6}},{0} \le {k} < {{{10} ^ {9}} + 7}\)

Solution

要使 \(x\) 最小肯定是 B 选择只 \(m\) 次 \(x + t\)。先考虑暴力 dp 怎么做，我们 只关心游戏进行的轮数已经 B 对于 \(x + t\) 的操作次数。

\(f_{i,j}\) 表示还剩下 \(i\) 个回合，B 要选择 \(j\) 次 \(x + t\) 时 A 还能获得的最大分数（另一种理解为当 \(n = i,m = j\) 时的答案）。从结束的状态倒推，有转移：

\[f_{i,j} = \max \limits_{{0} \le {t} \le {k}}{\{\min{\{f_{i-1,j} - t,f_{i-1,j-1} + t\}}\}} \]

感性理解一下，有 \({0} \le {f_{i-1,j} - f_{i-1,j-1}} \le {2k}\)（前提条件，说明 \(t\) 可以合法取得到 \(\large \frac{f_{i-1,j} - f_{i-1,j-1}}{2}\)，因此化简一下为 \(\large f_{i,j} = \frac{f_{i-1,j} + f_{i-1,j-1}}{2}\)。（相当于两杯水可以互相倒，使得最小值的最大化，就是取平均值）。

边界条件有 \(f_{i,0}=0,f_{i,i} = {i} \times {k}\)，可以做到 \(O(n^2)\)。

考虑每个 \(f_{i,i} = {i} \times {k}\) 对 \(f_{n,m}\) 的贡献，可以看成从 \((i,i)\) 走到 \((n,m)\)，每次可以向下或者向右走的方案数 \(g = \binom{n-i-1}{m-j}\)（由于 \((i,i)\) 不能向右走，因此有 \(n - i - 1\) 次向右走的机会，选择其中的 \(m - j\) 次），由于每次向下走一层都要除以 \(2\)，最后贡献为 \(\large \frac{g}{{2} ^ {n-i}}\)。

对组合数做预处理可以优化成线性复杂度，注意特判 \(n = m\) 的情况。

Reflect

若考虑设计 dp 状态为：\(f_{i,j}\) 表示经过 \(i\) 轮后 B 的已经操作 \(j\) 次 \(x + t\) 操作，A 所能达到的最大分数。

一般的博弈论 dp 题都是从后往前 dp，即从终止状态向初始状态 dp，因为采用最优策略使得双方都能预测当前的行为对后续状态的影响，所以说只有后效性，而没有前效性：若 \(i,j\) 确定，双方之前的决策对当前的决策无影响。

感觉博弈论的思考方向好神秘qwq

T3 P9192 [USACO23OPEN] Pareidolia P*

T4 P11989 [JOIST 2025] 勇者比太郎 3 / Bitaro the Brave 3*

10/12

T1 CF1795C Tea Tasting

题意

给定两个长度为 \(n\) 的序列 \(a,b\)，分别表示第 \(i\) 种茶的杯数和第 \(i\) 位品茶师每次至多喝 \(b_i\) 杯茶。

品茶师按编号顺序从小到大品茶，品茶大会进行 \(n\) 轮，第 \(i\) 轮时：

当前还剩下的第 \(i\) 位品茶师会喝掉 \(x = \min{\{a_i,b_i\}}\) 杯的第 \(i\) 种茶，同时 \({a_i} \gets {a_i - x}\)；
该轮结束时，本轮开始时的第 \(1\) 位品茶师会离场。

依次求出原来编号为 \(i\) 的品茶师喝的茶的杯数。

\({1} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i,b_i} \le {{10} ^ {9}}\)

Solution

对前 \(i\) 个品茶师的杯数上限维护前缀和 \(s_i\)。

考虑第 \(i\) 种茶对品茶师的贡献，有且仅有 \(x\) 满足前 \(x\) 轮时喝该种茶的品茶师都喝到了其杯数上限，还可能对第 \(x + 1\) 轮的品茶师产生部分贡献；

对 \(s_i\) 二分出 \(x\)，并运用差分记录即可，时间复杂度为 \(O(n\log{n})\)。

T2 CF1704E Count Seconds

题意

给定一个 \(n\) 个点 \(m\) 条边的有向无环图。该图中恰好有一个没有出边的点，第 \(i\) 个节点上有一个整数 \(a_i\)。

每一秒会发生如下操作：

设 \(S\) 为所有满足 \({a_x} > {0}\) 的节点 \(x\) 的集合。
对于所有 \({x} \in {S}\)，将 \(a_x\) 减去 \(1\)，然后对于每一个存在从 \(x\) 到 \(y\) 的边的节点 \(y\)，将 \(a_y\) 加上 \(1\)。

求所有点的 \(a_i\) 都变为 \(0\) 的最早时刻。

\({1} \le {n,m} \le {1000},{0} \le {a_i} \le {{10} ^ {9}}\)

Solution

先考虑若图上每个点都满足 \(a_i > 0\) 时的情况，出度为 \(0\) 的点 \(p\)。

由于每个点只会流出 \(1\) 点，每次流进的点数 \(\ge {1}\)，所以整个流动过程连贯，最早时刻就是当 \(a_p = 0\) 的时刻，很经典的拓扑排序。

但如果图上有 \(a_i = 0\) 的点，流动过程可能会不连贯，从而影响拓扑序的统计贡献。

图上的最长路径的大小 \(\le {n}\)，不妨暴力模拟前 \(n\) 秒的流动，在第 \(n + 1\) 秒时必然都满足 \(a_i > 0\)，再跑拓扑排序即可。

时间复杂度为 \(O(nm)\) 的，\(n,m\) 同阶。

Reflect

有向无环图，那么大抵和连通分量缩点没关系了。

\(n\) 是平方级别的，考虑特殊的限制后拓扑计算贡献是简单，又发现可以直接 \(O(n^2)\) 构造出特殊的限制。

T3 AT festival 2017_qualb_f*

T4 CF756E Byteland coins*

10/13

T1 P10059 Choose

题意

给定一个长度为 \(n\) 的序列 \(a\) 和一个正整数 \(k\)，选出 \(k\) 个不同的区间 \([l_i,r_i]\)（区间可以交叉，但不能包含），得到的分数为 \(\min \limits_{i=1}^{k}{\{\max \limits_{{l_i} \le {j} \le {r_i}}{a_j} - \min \limits_{{l_i} \le {j} \le {r_i}}{a_j}\}}\)，即区间的极差，最大化得到的分数，并求出在此分数下区间长度的最小值。

\({1} \le {n} \le {{10} ^ {5}},{1} \le {k} \le {n}\)

Solution

最坏的情况，全部区间都选最大长度，找到这些区间中的最大分数 \(x\)。

一个简单的方法就是发现第二个问题具有单调性，二分答案长度 \(d\) 即可，用 st 表维护区间最大最小值，可以做到 \(O(n\log{n})\)。

lgx 说还有一种线性做法！！！反正考场上没想到...

枚举所有可能得右端点 \(r\)，那么其左端点 \(l\) 必须满足 \([l,r]\) 的极差 \(\ge {x}\)，用双指针维护。

那么对于每一个右端点，都得到了一个可能的左端点 \([1,l]\)，区间长度取值为 \([r-l+1,r]\)，再维护一个差分数组 \(cnt\)，找到一个可能的最小区间长度，满足 \({cnt_i} \ge {k}\)，就可以实现 \(O(n)\) 了。

Reflect

一开始竟然没想到最大值是固定的？？？

得到最大值后其实就可以想到用二分判定即可。

T2 CF1495B Let's Go Hiking

题意

有一个长度为 \(n\) 的排列 \(a\)，表示山的位置 \(i\) 的高度。

A 选择一个起点 \({x_0} \in {[1,n]}\)并告诉 B，随后 B 选择一个起点 \(y_0\)，两人分别从 \(x_0,y_0\) 开始游戏。随后，A 和 B 轮流移动，A 第一个移动。记 \(x,y\) 为当前两人的位置:

若当前为 A 移动：A 需要选择一个位置 \(x'\) 满足 \({x'} \ne {y}\) 且 \(|x' - x| = 1\) 且 \({a_{x'}} < {a_x}\)，然后从位置 \(x\) 移动到位置 \(x'\)。
若当前为 B 移动：B 需要选择一个位置 \(y'\) 满足 \({y'} \ne {x}\) 且 \(|y' - y| = 1\) 且 \({a_{y'}} > {a_y}\)，然后从位置 \(y\) 移动到位置 \(y'\)。

若当前玩家无法进行移动，则视为其游戏失败。

求可以使得 A 存在必胜策略的初始位置的个数。

\({2} \le {n} \le {{10} ^ {5}},{1} \le {a_i} \le {n}\)

Solution

其实发现就是分类讨论题。

由于时间问题，这里不再赘述。（有时间再回来补）

有结论：

A 唯一能赢的情况为：有且仅有两条最长的边，刚好连在一起，且长度恰好为奇数。

维护前后缀最长上升子序列即可。

Reflect

双方博弈的分类讨论时多换位思考，考虑全面。

T3 P5102 [JOI 2016 Final] 领地 / Territory*

T4 P12486 [集训队互测 2024] 木桶效应*

10/14

T1 CF1919D 01 Tree

有一棵包含 \(n\) 个叶子节点的带边权二叉树，树上每个非叶子节点恰好有两个叶子节点，且与两个儿子的连边种，恰好一条边权为 \(0\)，另一条边权为 \(1\)。

给定一个长度为 \(n\) 的非负整数序列 \(a\)，\(a_i\) 表示从根节点到第 \(i\) 个叶子节点的的路径权值力和。

请注意，这里叶子的编号是按照树上 dfs 顺序排的，具体的，执行以下代码，得到的数组 dfs_order 即为编号为 \({i} \in {[1,n]}\) 的叶子在原树上的编号。

dfs_order = []

function dfs(v):
    if v is leaf:
        append v to the back of dfs_order
    else:
        dfs(left child of v)
        dfs(right child of v)

dfs(root)

判断是否存在一个满足条件的二叉树。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}},{0} \le {a_i} \le {n-1}\)

Solution

有点构造的意思？？？

由题意可以得到，同父亲的两个叶子节点的 \(|a_{ls} - a_{rs}| = 1\)，若将这两个点合并成一个点，则新的叶子结点的权值为 \(\min{\{a_{ls},a_{rs}\}}\)。不断重复合并的过程，发现最后必然只剩下一个 \(0\)。

考虑一个点权都为 \(x=a_l\) 的连续段 \([l,r]\)，若 \({a_{l-1} = a_l - 1} \lor {a_{r+1} = a_r - 1}\)，则这一段数都可以向左边或右边一直合并，这一部分构造的二叉树形态为：

CF1919D

进而推出：对于 \(a_i\) 覆盖的最大区间 \([l,r]\) 满足 \(\forall {{j} \in {[l,r]}},{{a_j} \ge {a_i}}\)，都能合并成一段值为 \(a_i\) 的数。判定每个 \(a_i\) 的区间是否都能向上合并即可，用单调栈维护区间左右端点，时间复杂度为 \(O(n)\)。

Reflect

维护区间最大/小值时别忘了单调栈。

T2 CF1936B Pinball

题意

有一个长度为 \(n\) 的一维网格，第 \(i\) 个格子中包含一个字符 \(s_i\)，该字符要么是 <，要么是 >。

当在某个格子上放置一个弹珠时，弹珠会按照以下规则移动：

如果弹珠当前在第 \(i\) 个格子且 \(s_i\) 是 <，则下一秒弹珠会向左移动一个格子；如果 \(s_i\) 是 >，则向右移动一个格子。
弹珠移动后，\(s_i\) 的字符会反转（即如果 \(s_i\) 原本是 <，则变为 >，反之亦然）。
当弹珠离开网格（即从左边界或右边界离开）时，弹珠停止移动。

\(n\) 个独立的询问，在第 \(i\) 个询问中，弹珠会被放在第 \(i\) 个格子上。注意，每次都在初始网格上放置弹珠。

对于每个询问，求弹珠离开网格所需的秒数。可以证明，弹珠总能在有限步内离开网格。

\({1} \le {n} \le {{5} \times {{10} ^ {5}}}\)

Solution

很容易可以看出来其实就是一个弹珠不断向两边来回撞，若一个位置被弹珠经过后，就不会再阻碍弹珠的移动。

考虑如何记录移动的距离，画一下图分类讨论即可（有时间补，且细节多，理解巧妙）：

..........

预处理左右的 < 和 > 的位置以及维护其前缀和，最后用二分再计算贡献即可。

Reflect

打草稿作图时可以画得清晰点，分析清楚再去写代码！！！

二分不一定要用手打的啊啊啊（时间充足或者情况特殊可以）：

第一个 \(< x\) 的数：lower_bound 再减 \(1\)。
最后一个 \(\le {x}\) 的数：upper_bound 再减 \(1\)。

其实还有很多操作，记得运用好这两个函数就可以了。

T3 P9522 [JOIST 2022] 错误拼写 / Misspelling

题意

给定 \(m\) 个二元组 \((a_i,b_i)\)，有一个长度为 \(n\) 的字符串 \(s\)，满足一下条件：

令 \(t_i\) \(({1} \le {i} \le {n})\) 为 \(s\) 删去第 \(i\) 个字符并将前后字符相接所得的字符串。对于每个 \(j\) \(({1} \le {j} \le {m})\) 满足 \({t_{a_j}} \le {t_{b_j}}\)。

其中 \({t_{a_j}} \le {t_{b_j}}\) 表示 \(t_{a_j}\) 等于 \(t_{b_j}\) 或 \(t_{a_j}\) 在字典序上小于 \(t_{b_j}\)。

求可能的 \(s\) 的个数。

\({2} \le {n} \le {{5} \times {{10} ^ {5}}},{1} \le {m} \le {{5} \times {{10} ^ {5}}},{a_j} \ne {b_j}\)

Solution

考虑 \({t_{a_j}} \le {t_{b_j}}\) 的等价条件，模拟字符串比较的过程：

若 \({a_j} < {b_j}\)，相当于 \(s_{[a_j,b_j]}\) 中第一个 \({s_x} \ne {s_{x+1}}\) 的位置 \(x\) 需要满足 \({s_x} > s_{x+1}\)，或者不存在 \(x\)。
若 \({a_j} > {b_j}\)，相当于 \(s_{[a_j,b_j]}\) 中第一个 \({s_x} \ne {s_{x+1}}\) 的位置 \(x\) 需要满足 \({s_x} < s_{x+1}\)，或者不存在 \(x\)。

称 \(a_j < b_j\) 的限制为第一类约束区间 \([a_j,b_j)\)；否则为第二类约束区间 \([b_j,a_j)\)。

记 \(f_{i,j}\) 表示考虑完前 \(i\) 个字符，\(s_i = j\) 的方案数。分类讨论转移（\({i} \to {i+1}\)）：

\(s_i = s_{i+1}\)：没有约束，\({f_{i,j}} \to {f_{i+1,j}}\)
\(s_i > s_{i+1}\)：
- 枚举上一个满足 \({s_k} \ne {s_{k+1}}\) 的位置 \(k\)，不能存在第二类约束区间满足 \({k} < {l} \le {i} \le {r}\)，那么合法的 \(k\) 是一段后缀，可以用 set 和扫描线思想维护这段后缀。
- 得到合法后缀后，每个 \(k\) 都有 \({f_{k+1,j} - f_{k,j}} \to {f_{i+1,[x < j]}}\)。反过来计算贡献，对于 \(x\)，发现对后缀上所有的 \(k\) 的贡献相加后中间的数都能抵消掉，变为 \(f_{i,j} - f_{k,j}\)，总方案数为 \(f_{i+1,x} = \sum \limits_{j > x}{f_{i,j} - f_{k,j}}\)，这个倒序做到 \(O(1)\) 转移。
\(s_i < s_{i+1}\)：类似可以推出，略。

总时间复杂度为 \(O(n|\Sigma| + n\log{n})\)，其中 \(|\Sigma| = 26\)。

Reflect

遇到多约束的题，考虑约束之间的是否能同时存在性。

字符串 dp，可以多考虑有一维为表示第 \(i\) 位的字符。

考虑贡献相加是否有抵消等性质，且可以用前缀和等优化转移。

T4 CF1919F2 Wine Factory (Hard Version)^

10/15

T1 AT_arc122_d [ARC122D] XOR Game~

题意

黑板上写有 \(2n\) 个整数，其中第 \(i\) 个整数为 \(a_i\)。

A 和 B 进行一场游戏。游戏共进行 \(n\) 轮，每一轮进行如下操作：

首先，A 从黑板上选择一个整数并将其擦除。设被选中的整数为 \(x\)。
接着，B 从黑板上选择一个整数并将其擦除。设被选中的整数为 \(y\)。
将 \({x} \oplus {y}\) 的值记录在笔记本上。这里的 \(\oplus\) 表示按位异或运算。

最终，黑板上的所有整数都会被擦除，笔记本上会记录下 \(n\) 个整数。游戏的得分为笔记本上记录的整数中的最大值。A 想最大化得分，B 想最小化得分。

当双方都采取最优策略，求最终游戏的得分。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}},{0} \le {a_i} < {{2} ^ {30}}\)

Solution

优先抵消掉最高位对于 B 必然是最优的，因为 \({{2} ^ {x}} > {\sum_{i=0}^{x-1}{{2} ^ {i}}}\)。

从高位到低位考虑，记 \(cnt_i\) 表示二进制下从右往左的第 \(i\) 位为 \(1\) 的数的个数。现在位于第 \(i\) 位：

若 \(cnt_i\) 是偶数，则 A 无论如何选择，这一位必然会被 B 抵消掉，没有贡献；
若 \(cnt_i\) 是奇数，则必然有一个数至少在第 \(i\) 位有贡献。

思考第二种情况，由于 B 是后手，一定可以使得 A 选择最劣的方案，假设最后 A 选择了 \(x\)，那么和 \(x\) 异或的只能是剩下的第 \(i\) 位为 \(0\) 的数，取最小值即可。很显然可以用字典树维护，并实现对配对最小值的查询。

时间复杂度为 \(O({2} \times {30} \times {n})\) 的。

讲一下怎么维护与 \(x\) 配对的最小值（以前没怎么认真学过？？？）：

带着符合条件的数集 \(S\) 在字典树 \(f_{p,0/1}\) 上从高位往低位走，当前位于第 \(i\) 位，假设 \(x\) 的第 \(i\) 位为 \(1\)，采用贪心的思想。

若 \(S\) 中存在在第 \(i\) 位为 \(1\) 的数，那么 B 在这一位上就必选 \(1\)，异或抵消掉 A 的 \(1\)。接下来，将 \(S\) 中第 \(i\) 为 \(1\) 的数组成集合 \(S'\)，向下一个点转移 \({p} \gets {f_{p,1}}\)；若不存在，则 A 这一位必然有贡献 \({2} ^ {i}\)，并 \({p} \gets {f_{p,0}}\)

\(x\) 第 \(i\) 位为 \(0\) 同理。

综上，可以得到：

inline int query(int x) {
	int p=0,res=0;
	for(int i=30;i>=0;i--) {
		int tem=(x>>i)&1;
		if(f[p][tem])
			p=f[p][tem];
		else {
			res+=(1<<i);
			p=f[p][tem^1];
		}
	}
	return res;
}

Reflect

想了有小段时间才能想到从高往低去判定奇偶性分讨论，在实现时也没有合理运用性质，还有那个维护配对最小值。

新的方法：遍历字典树的时候，用 vector 维护合法的集合。

遇到这种二进制问题时，可以想的方面：

字典树
拆位
状压dp

T2 P7334 [JRKSJ R1] 吊打~

题意

给出一个长为 \(n\) 的正整数序列 \(a_{{1} \sim {n}}\)。接下来有两种操作共 \(m\) 次：

1 l r，表示将 \(a_{{l} \sim {r}}\) 开方并下取整，即令 \(\forall {{i} \in {[l,r]}},{{a_i} \gets {\lfloor {\sqrt{a_i}} \rfloor}}\)；
2 l r，表示将 \(a_{{l} \sim {r}}\) 平方，即令 \(\forall {{i} \in {[l,r]}},{{a_i} \gets {{a_i} ^ {2}}}\)。

在所有操作结束后，求 \(\displaystyle \sum_{i=1}^{n}{a_i}\)。对 \(998224353\) 取模。

\({1} \le {n,m} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}}\)

Solution

小清新势能线段树题，好妙啊。

先考虑操作 1，暴力对叶子节点信息向下开方取整，并加入限制，若区间 \([l,r]\) 的 \(\max\) 为 \(1\) 时，就不需要继续修改了，而且这时候对于操作 2 的平方起同效作用，每个叶子结点开方最多 \(\log{\log{V}}\) 次，是双对数级别的。

再考虑操作 2，因为对一个数平方后再开方，数是没有改变的，不放记录区间最小的平方次数 \(pw\) 和向下传递的懒标记 \(tag\)，不着急对数直接做平方操作。

若在执行操作 1 时，遇到区间 \([l,r]\) 的 \({pw} \ge {1}\)，直接将 \(pw,tag\) 都减去 \(1\) 就可以了；否则就一直遍历到底部的叶子节点，再如上述所说暴力开方取整，势能依旧为 \(O(\log{\log{V}})\)。（想想这步操作，超级妙）

最后时单点查询并对每个数的贡献相加，若对于数 \(x\)，有 \({{{x} ^ {2}} ^ {pw}}\)，运用欧拉降幂快速求解即可。

时间复杂度为 \(O(n(\log{n}+\log\log{n}))\)。

关于欧拉降幂：

由扩展欧拉定理可知，当 \({a} \perp {m}\) 时，有 \({{{a} ^ {b}} \equiv {{a} ^ {{b} \bmod {\varphi{(m)}}}}} \pmod {m}\)，由于 \(m = 998244353\) 时质数，所以 \(\varphi{(m)} = m - 1\)，再用快速幂求解即可。

Reflect

考场上昏昏的，没巧妙想到两个操作可以互相抵消，其实最后势能只关乎就是操作 1，还有最后的欧拉降幂技巧要记住。

T3 CF2063F2 Counting Is Not Fun (Hard Version)~

题意

有一个长度为 \(2n\) 的合法括号序列，给定 \(n\) 个整数二元组 \((l_i,r_i)\)，满足 \(\forall {{i} \in {[1,n]}},{{1} \le {l_i} < {r_i} \le {2n}}\)，且所有整数互不相同，表示在第 \(i\) 轮插入一对匹配的括号，左括号位于 \(l_i\)，右括号位于 \(r_i\)。

求在初始时，以及在每一轮之后可能的合法括号序列数量。

保证每一轮之后，一定存在至少一个合法的括号序列。

\({2} \le {n} \le {{3} \times {{10} ^ {5}}}\)

Solution

如果没钦定的情况就是普通的括号序列计数，套卡特兰数即可。

可以看做在两边先强行塞上一对括号 \([0,2n + 1]\)，将每对括号 \([l_i,r_i]\) 看作是树上一个节点 \(i\)，将每个对括号向被被他包含的下一层括号连边，就能得到一棵树，长度为 \(len_i = r_i - l_i + 1\)。插入过程中树上的一个点 \(u\) 内能放置的括号数量就是 \(val_u = len_u - 2 - \sum_{{v} \in {son(u)}}{len_v}\)。

(((())()(())))

(1(22)11(22)1)

注：数字代表所在的层数。

发现不同层上放置括号的方案是独立的，否则就破坏了插入的括号的匹配顺序，如：

((()2)11(22)1)

这样就变成了 \((2,4)\) 配对，\((3,6)\) 配对，但是刚刚插入时已经固定了 \((3,6)\) 匹配。

因此同一层 \(i\) 上的方案数为 \(\prod_{i}{Cat_{val_i}}\)。

发现实质上是往树上加点，不好做。不妨倒着做，删点，转化为删一个点 \(u\) 并将其所有儿子连到其父亲 \(fa_u\) 上，一次修改只会影响 \(u\) 和 \(fa_u\) 的 \(val\)，用并查集快速维护一个点当前的父亲，删去 \(u\) 时就将 \(u\) 和 \(fa_u\) 合并成一个点。

初始时用单调栈去维护最后长度为 \(2n\) 的合法括号序列中第 \(i\) 个序列的儿子括号区间，预处理 \(fa\) 即可，时间复杂度为 \(O(n\alpha{(n)})\)。

Reflect

处理括号序列匹配的方法：

单调栈
并查集

新思想：括号序列可以构成一棵树。

考虑残缺的括号序列时，多想想层与层已经本层直接的数量关系。

T4 P9598 [JOI Open 2018] 山体滑坡 / Collapse*

10/16

T1 P9202 「GMOI R2-T2」猫耳小（加强版）

题意

给定一个长度为 \(n\) 的序列 \(a\)，可以任意修改 \(a\) 中的若干个元素为任意自然数，求最小化修改元素数量，使得 \(a\) 的任意连续非空子串的 \(\mathrm{mex}\) 都不等于 \(k\)。

\({1} \le {n} \le {{10} ^ {6}},{0} \le {k,a_i} \le {{10} ^ {9}}\)

Solution

很显然处理两个相邻 \(k\) 之间的区间，因为跨过值为 \(k\) 的区间显然都合法，若发现一个区间存在 \([0,k)\)，那么将区间内任意一个数改为 \(k\) 就可以使得这个区间变得合法。

最优的改法必然是选择区间的右端点，那么思路就顺势而来：

对于以 \(k\) 为分界线的一段区间 \([l,r]\)，从左往右扫，遇到一个极小的不合法区间，将右端点改成 \(k\)，并加入贡献点即可，这里可以用 set 维护，修改右端点后，直接将 set 清空即可（map 也可以）。

时间复杂度为 \(O(n\log{n})\)，瓶颈在 set 上。

Reflect

没有一眼就看出来qwq，一开始想着是将两个值为 \(k\) 之间有 \([0,k)\) 的出现次数最少的数改为 \(\inf\)，而且后面想出来了还用线段树做了 set 的工作...

T2 CF1610E AmShZ and G.O.A.T.

题意

给定一个长度为 \(n\) 的序列 \(a\)，记 \(x = \sum_{i=1}^{n}{[a_i > \bar{a}]},y = \sum_{i=1}^{n}{[a_i < \bar{a}]}\)。

若 \(x > y\) 则称这个序列是坏的。

最小化删除的元素个数，使得没有一个子集是坏的。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}}\)

Solution

观察条件，如果只选出三个数的子集，那么中间的数一定小于等于两边的数的平均值，即若 \({x} \le {y} \le {z}\)，那么有 \({z - y} \ge {y - x}\)。

对 \(a\) 从小到大排序，考虑枚举最终的集合中最小的数 \(s\)，向后枚举可能选择的数 \(x\)，当前集合中最大的数为 \(t\)，那么应该满足 \({x - t} \ge {t - s}\)，根据贪心的思想，一定是能选就选。

不难发现，由于每次选择近乎可以看做 \(\times {2}\)，所以选择的数量为 \(\log\) 级别的，每次都对下一个选择的数二分即可。

注意，需要特殊处理初始时出现多个值为 \(s\) 的数，否则会导致时间复杂度错误。

时间复杂度为 \(O(n\log{n}\log{V})\)。

Reflect

遇到序列的题，没思路时不妨缩小序列长度，猜、找性质。

要考虑性质的增长性，单调性。

尝试钦定最小值，然后枚举（考虑是否能做到单/双 \(\log\) 或者 \(\sqrt{n}\) 的），还可以进而再钦定已经选取的集合中的最大值或者其他性质需要的数，辅助思考。

T3 P12426 [BalticOI 2025] BOI acronym

前文讲过qwq

T4 P7416 [USACO21FEB] No Time to Dry P~

题意

有一排 \(n\) 个格子，每个格子都需要被染成一个颜色，其中第 \(i\) 个格子需要被染成颜色 \(a_i\)。

可以进行多轮染色，每一轮将区间 \([l,r]\) 的格子染成颜色 \(c\)，其中 \({l,r,c} \in {\mathbb{{N} ^ {+}}}\)。

一个格子可以被多次染色，若已被染成了颜色 \(x\)，再染成颜色 \(y\) 时，需满足 \({x} \le {y}\)。

\(q\) 次询问 \((l_i,r_i)\)，仅给区间 \([l_i,r_i]\) 上的格子染成对应的颜色的最小染色轮数。

\({1} \le {n,q} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i} \le {n}\)

Solution

很显然，对于两个需要染成相同颜色的格子 \(i,j\)，若 \({k} \in {(i,j)}\) 满足 \({a_k} > {a_i}\)，那么这两个格子可以在同一轮被染色。

对于每个格子 \(i\)，明显只用考虑前面第一个 \(a_j = a_i\) 的格子 \(j\)，若两个格子可以在同一轮被染色，不妨加入区间 \([j,i]\)。

一次询问 \((l_i,r_i)\) 的贡献其实就是 \(r_i - l_i + 1 - cnt\)，其中 \(cnt\) 为区间 \([l_i,r_i]\) 中无交集的区间个数。

用扫描线做二维数点即可，这里可以用树状数组维护差分来做，时间复杂度为 \(O((n+q)\log{n})\)。

Reflect

一开始想着的是：若两个相同颜色的格子之间有更小的数，那么次数就要加 \(1\)。其实可以做吧？？？但是场上没打。

正着不好处理，考虑反着来：
- 时光倒流；
- 容斥中"至少"等；
- < 变 >，加贡献变成减贡献。

记住可以多用树状树组维护差分，而且扫描线不是板板的，可以多变的。

区间计数，算贡献，可以往扫描线上想。

10/17

T1 AT_arc119_c [ARC119C] ARC Wrecker 2

题意

给定一个长度为 \(n\) 的序列 \(a\)，有操作:

选择一个整数 \(x\) 满足 \({1} \le {x} < {n}\)，令 \(a_i,a_{i+1}\) 同时加 \(1\)；
选择一个整数 \(x\) 满足 \({1} \le {x} < {n}\)，令 \(a_i,a_{i+1}\) 同时减 \(1\)。

求满足以下条件的有序二元组 \((l,r)\) 个数：

\({1} \le {l} \le {r} \le {n}\)；
序列 \(a\) 的区间 \([l,r]\) 组成的新序列，可以通过若干次操作，且中途任何时刻任何元素不能为负数，最终所有元素都变成 \(0\)。

\({2} \le {n} \le {{3} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}}\)

Solution

由于可以用操作一对数无限加，且操作次数没有限制，所以任何时刻任何元素不能为负数的要求可以省略掉。

接下来，考虑对能用操作二使得区间内所有元素变成 \(0\) 进行计数。由于 \(r\) 是不能操作的，所以前一个数 \({a_{r-1}} \gets {a_{r-1} - a_r}\)（这里已经可以不用判断是否 \(< 0\) 了）。

推导一下式子，可以发现其实就是奇数位上的数赋权值为 \(-1\)，偶数位上的数赋权值为 \(1\)，前缀和维护一下，再用 unorder_map 记录 + 差分思想统计贡献即可。

时间复杂度为 \(O(n)\)。

Reflect

一开始没有直入正题省略去不能为负数的要求，导致推式子的时候要和 \(0\) 取 \(\max\)，不好维护。

小技巧，从 不变量 上入手，也就是操作不会改变什么。

发现 交错和 是不变的，那就变成了求交错和等于 \(0\) 的区间个数。

交错和：\(S = \sum_{k=0}^{n}{{(-1)} ^ {k}a_k}\)。

其实直接就从奇偶性入手做就很简单了。

下面是 lgx 提到的做法：

具体来说，我们可以任意选择两个奇偶性相同的位置，一个 \(+1\) 一个 \(—1\)；或者选择两个奇偶性不同的位置，同时 \(+1\) 或同时 \(—1\)。所以一个数组合法的充要条件为，奇位置上的数字总和等于偶位置上的数字总和。

设 \(s\) 表示前个位置，奇位置上的数字总和减去偶位置上的数字总和的结果，\([l,r]\) 合法当且仅当\(s_r=s_{l—1}\)，直接计数即可。

T2 P10100 [ROIR 2023] 石头 (Day 2)

题意

排列着 \(n\) 个黑色的石头，从 \(1\) 到 \(n\) 编号，并给定一个长度为 \(n\) 的排列 \(a\)，表示每个石头上的数字。

按照以下步骤进行 \(n\) 次操作：

第 \(1\) 步选择一个数 \(i\)，并将第 \(i\) 个石头染成白色，并将该石头称为初始石头；
接来下的每一步，选择被染成白色的石头相邻没被染色的石头中数字最小的石头 \(j\)，并将其染成白色。

\(q\) 次询问 \((p_j,k_j)\)，求使得第 \(k_j\) 步被染成白色的石头编号为 \(p_j\) 的初始石头数量。

\({2} \le {n} \le {{10} ^ {5}},{1} \le {q} \le {{10} ^ {5}},{1} \le {a_i,p_j,k_j} \le {n}\) 且 \(a_i\) 互不相同。

Solution

考虑一次询问 \((p_j,k_j)\)，那么已经染色的石头编号为 \([p-k+1,p]\) 或者 \([p,p+k-1]\)，这两部分是独立且相似的。

可以把 \(a_i\) 值的大的位置视作有墙，先考虑 \([p-k+1,p]\)，令区间最大值的下标为 \(x\)，\(l = p - k + 1,r = p\)：

若 \(a_{l-1} > a_x\)，则对于区间 \([l,r]\) 来说位置 \(l - 1\) 上有墙，想要对 \(l - 1\) 上的石头染色，\([l,r]\) 必然已经被染色：
- 显然的，\((x,r]\) 上的所有位置都是不合法的。
- 由于 \(a_x\) 是区间 \([l,r]\) 上最大的数，则对于 \([l,x),(x,r]\) 来说，位置 \(x\) 也有墙，且 \([l,x)\) 左右都有墙，当起始石头的位置选择在 \([l,x)\) 时，一定能先染完所有 \([l,x)\) 中所有的石头，再往右边染色，以此染色到 \(r\)，故贡献为 \(x - l\)。
- 考虑位置 \(x\) 是否合法，再令 \([l,x),(x,r]\) 的最大值分别为 \(lx,rx\)：
  - 若 \(x = l\)，显然合法。
  - 若 \(lx < rx\)，从 \(x\) 染色到 \(rx\) 时必然会先回到左边 \([l,x)\) 染色，且当 \([l,x)\) 全部被染完色后才会从 \(rx\) 依次染色到 \(r\)，合法。
  - 若 \(lx > rx\)，跟上述相反，\(r\) 的染色优先级比 \([l,lx]\) 高，不合法。

同理，\([p,p+k-1]\) 的计数也类似，不再赘述。

用 st 表维护区间最大值的位置即可，时间复杂度为 \(O(n\log{n} + q)\)。

Reflect

想到了那个“墙”的性质，但是没能想到直接对区间的最大值位置分类讨论计数，而是想单调栈维护 \(p\) 左右 \(> p\) 的位置，然后二分边界值，然后计算贡献，比较麻烦qwq

感觉自己总是把做法想复杂，考场上别再这样了qwq

染色过程可以看做左右扩展，而墙（最大值）具有限制左右扩展的作用，这个性质应该要想到，再分类讨论计数即可。

T3 CF1781F Bracket Insertion*

没什么时间实现qwq

Solution

将概率转化为方案数。大体思路就是将 ( 和 ) 视为 \(1\) 和 \(-1\)，对括号序列做前缀和，每个值都是非负数。

考虑前缀和形成的多重集 \(s\)：

插入 ()，相当于选择一个 \(x\)，插入 \(x\) 和 \(x + 1\)；
插入 )(，相当于选择一个 \(x\)，插入 \(x\) 和 \(x - 1\)。

插入的过程可以视作一棵有根树，在树上对插入的过程进行 dp 转移即可。

Reflect

小思想，像括号具有匹配的性质的序列可以考虑设置 \(1\) 和 \(-1\)，考虑前缀和。

上述中向多重集 \(s\) 中插入 \(x\) 和 \(x + 1\)（或者 \(x - 1\)），很关键，但又是不容易想得到的。

T4 P10880 [JRKSJ R9] 莫队的 1.5 近似构造*

10/18

T1 P5329 [SNOI2019] 字符串

题意

给出一个长度为 \(n\) 的由小写字母组成的字符串 \(s\)，设其中第 \(i\) 个字符为 \(s_i(1\le i\le n)\)。

设删掉第 \(i\) 个字符之后得到的字符串为 \(t_i\)，请按照字典序对 \(t_1,t_2,\ldots,t_n\) 从小到大排序。若两个字符串相等，则认为编号小的字符串字典序更小。

\({1} \le {n} \le {{10} ^ {6}}\)

Solution

容易想到 \(t_n\) 是个特殊的存在，因为删去 \(s_n\) 无法对后面的字符进行比较，所以 \(t_n\) 可以视作一个分界线。

考虑 \(s_i\) 和 \(s_{i+1}\)：

\({s_i} > s_{i+1}\)：则 \({t_{i}} < {t_{i+1}}\)，显然 \({t_i} < {t_n}\)，放在 \(n\) 前，且比后面的 \(t_j,{j} \in {(i,n]}\) 都小。
\({s_i} < s_{i+1}\)：则 \({t_i} > {t_{i+1}}\)，且 \({t_i} > {t_n}\)，放在 \(n\) 后，但是可能会和后面的 \(t_j\) 相等，这时候 \(i\) 是字典序更小的一个：
- \(t_i\) 和 \(t_j\) 相等的前提条件为 \(\forall {{k} \in {(i,j]}},{s_k = s_i}\)；由此，只需要维护一段满足条件的区间，再将这个区间内的 \(t\) 按编号从小到大再排一遍即可。
\(s_i = s_{i+1}\)，则需要判断 \(i\) 与后面第一个 \(j\) 满足 \({s_j} \ne {s_i}\) 的大小关系：
- 若 \({s_i} > {s_j}\)，同上述的第一类情况；
- 若 \({s_i} < {s_j}\)，第二类情况。

综上，实质就时判断 \(t_i\) 与后面的 \(t_j\) 之间的字典序大小，判断的依据就是 \((i,n]\) 中第一个与 \(s_i\) 不一样的位置，时间复杂度为 \(O(n)\)。

其实有更加简单实现的 \(O(n\log{n})\) 做法，但是考场上没打出来，

Reflect

没有一下子点出解法的实质，对于第二、三类情况的分类不仔细。

T2 CF1896E Permutation Sorting

题意

有 \(n\) 个奶牛，编号为 \({1} \sim {n}\)，所属牛栏的编号分别为 \({1} \sim {n}\)，并且按照编号顺时针围城一个圈。

给定长度为 \(n\) 的序列 \(a\)，表示编号为 \(a_i\) 的人处于编号为 \(i\) 的牛栏的位置。

进行若干轮以下的操作：

每一轮，令 \(\forall {{j} \in {[1,k]}},{b_j}\) 表示还没回到所属牛栏的奶牛的编号；处于编号为 \(b_j\) 的牛栏的奶牛会移动到处于编号为 \(b_{{{j} \bmod {k}} + 1}\) 的牛栏的位置上。

求每个人第一次回到家需要经过的轮数。

\({1} \le {n} \le {{10} ^ {6}},{1} \le {a_i} \le {n}\)

Solution

套路的，对于先断环成链，考虑 \({i} \to {a_i}\) 的过程中，若没有其他的奶牛回到牛栏，那么轮数为 \(a_i - i\)；若有一个奶牛 \(a_j\) 回到了所属牛栏，那么奶牛 \(a_i\) 将会跳过 \(a_j\) 这个位置，轮数将减少 \(1\)。

令 \(l_i = i,r_i = a_i\)，\([l_i,r_i]\) 中满足 \({l_i} \le {l_j} \le {r_j} \le {r_i}\) 的位置 \(j\) 的个数为 \(x\)，由上可以得到 \({l_i} \to {r_i}\) 的轮数为 \(r_i - l_i - x\)。

二维数点，用树状数组维护即可，时间复杂度为 \(O(n\log{n})\)。

Reflect

考场上不想做断环成链的题，感觉很复杂，其实一般来说画画图，表示出来区间，考虑如何维护贡献就容易很多了。

T3 CF1889D Game of Stacks*

T4 CF1610G AmShZ Wins a Bet*

10/20

起风了。

收到祝福，开心qwq

T1 CF1852A Ntarsis' Set

题意

初始有一个集合 \(S = \{1, 2, 3, \ldots, {10} ^ {1000}\}\)。

每轮同时移除 \(S\) 中第 \(a_1\) 小，第 \(a_2\) 小，\(\ldots\)，第 \(a_n\) 小的数。

经过 \(k\) 轮后，\(S\) 中元素的最小值。

\({1} \le {n,k} \le {{2} \times {{10} ^ {5}}},{1} \le {a_i} \le {{10} ^ {9}}\)

数据可以加强为 \({1} \le {k} \le {{10} ^ {9}}\)。

Solution

发现删除操作实质是在降低剩余数字的排名，故不断减去 \(\le {a_i}\) 个数，即 \(a_i\) 在该轮降低的排名。

考虑时光倒流，从最后一轮开始依次往前考虑，最终的最小值在第 \(k\) 轮时排在第 \(1\) 位。

若在该天之后排在第 \(x\) 位，找到最大的 \(i\) 满足 \({a_i} \le {x + i - 1}\)，那么在该天之间变为 \({x} \gets {x + i}\)。随着 \(x\) 的变大，\(i\) 也会变大，枚举每个 \(i\) 然后钦定为其为满足条件最大的 \(i\)，显然 \(i\) 的贡献是一段连续的轮数，反过来计算 \(a_i\) 对 \(x\) 的贡献即可。

时间复杂度为 \(O(n)\)。

Reflect

由于实质是降低排名，考虑到最后的答案必然在最后一轮排第 \(1\) 位，已经固定，那就可以时光倒流，倒推回去，也算一种套路了？？？

T2 CF1936C Pokémon Arena

题意

现在处于一个对战竞技场，并且有 \(n\) 只宝可梦。最初，只有第 \(1\) 只宝可梦站在竞技场上。

每只宝可梦有 \(m\) 个属性。第 \(i\) 只宝可梦的第 \(j\) 个属性为 \(a_{i,j}\)。

每只宝可梦都有一个雇佣费用：第 \(i\) 只宝可梦的费用为 \(c_i\)。

可以按任意顺序、任意次数执行以下两种操作：

选择 \((i,j,k)\)，将 \(a_{i,j}\) 永久增加 \(k\)。该操作的费用为 \(k\)。
选择 \((i,j)\)，雇佣第 \(i\) 只宝可梦与当前站在竞技场上的宝可梦以第 \(j\) 个属性进行对战。如果 \(a_{i,j}\) 大于等于当前竞技场宝可梦的第 \(j\) 个属性，则第 \(i\) 只宝可梦获胜（否则失败）。对战后，只有获胜者留在竞技场。该操作的费用为 \(c_i\)。

求使第 \(n\) 只宝可梦站在竞技场上所需支付的最小费用。

\({2} \le {n} \le {{4} \times {{10} ^ {5}}},{1} \le {m} \le {{2} \times {{10} ^ {5}}},{2} \le {{n} \times {m}} \le {{4} \times {{10} ^ {5}}}\)

\({1} \le {c_i,a_{i,j}} \le {{10} ^ {9}}\)

Solution

看到按属性优先级比较，很显然的建图跑最短路。

直接建图就是每个宝可梦之间都可以连边加权，边数过多，考虑优化建图。

考虑对每个宝可梦的每一个属性都建立一个点，同一只宝可梦的每个属性点之间连一条边权为 \(0\) 的边。

发现任意两个属性点之间都连边太多冗余，不妨对同属性点按 \(a\) 从小到大排序，用一条链连起来，边权为相邻两点的差值。

点数和边数都是 \(\Theta {(nm)}\) 级别的，时间复杂度为 \(O(nm\log{nm})\)。

Reflect

优化建图小技巧：若多条边之间有重叠的部分，不妨拆开成链连接，不影响两点之间的最短路径权值和。

T3 CF983E NN country*

T4 AT_code_festival_2017_qualc_f Three Gluttons*

10/21

难得给了一天喘息，复习了矩阵快速幂。

10/22

魔方破了两次 PB（都是使用“魔域文化”）：

不跳步：\(24.89s\)

首次突破 \(25s\)

时间：下午，地点：科学楼 \(5\) 楼靠桥的走廊，音乐：带我走

跳步（倒数第二步）：\(23.29s\)

时间：晚上 \(11:20\)，地点：宿舍 621，音乐：带我走

T1 P9464 [EGOI 2023] Padel Prize Pursuit / 追梦笼式网球

题意

有 \(n\) 个人，共有 \(m\) 天的比赛，每天进行一场对决，第 \(i\) 天进程如下：

\(x_i\) 击败 \(y_i\)；
\(x_i\) 获得奖牌 \(i\)；
\(x_i\) 同时拿走 \(y_i\) 身上的所有奖牌。

在所有比赛结束后，第 \(i\) 块奖牌会奖给获得这块奖牌时长最长的人，求每个人最终获得的奖牌数量。

\({2} \le {n} \le {{2} \times {{10} ^ {5}}},{1} \le {m} \le {{2} \times {{10} ^ {5}}}\)

Solution

单独观察奖牌 \(i\)，若其第一次被其他人拿走时的时间为第 \(j\) 天，那么其后面进行的移动都和奖牌 \(j\) 一样了，那不妨倒过来从最后拥有奖牌的人转移过来。

发现关系直接构成了森林，而钦定每棵树最后拥有奖牌的点为该树的根。

每次从根开始走，\(sum_i\) 表示遍历到点 \(u\) 时第 \(i\) 个人拥有奖牌 \(u\) 的时长，再用 set 维护当前拥有时长最长的人。

进入点 \(u\) 时，更新 \(sum\) 并加入 set，离开后恢复进入前的 set 状态即可。

时间复杂度为 \(O(n\log{n})\)，瓶颈在于 set。

其实也可以做到线性的（发现只需要维护 \(sum\) 的最大值）。

Reflect

想到从后往前处理，一开始将关系反过来建了，建出来的图并非森林，而是 DAG。

T2 CF1310D Tourism

题意

给定一个 \(n\) 个点的完全图，求经过点 \(1\)，点数为 \(k\)，不含奇环，可以重复经过点和边的最小边权和环路。

\({2} \le {n} \le {80},{2} \le {k} \le {10}\) 且 \(k\) 是偶数。

Solution

由于 \({k} \le {10}\)，意味着真正对结果产生贡献的节点至多有 \(10\) 个。

且题目要求 没有奇环，容易想到二分图黑白染色的性质。

考虑对每个点随机黑/白染色，强制走两端颜色不相同的边。

\(f_{i,j}\) 表示走了 \(i\) 条边，当前位于点 \(j\) 的最小花费，\(O(n^2k)\) 转移。

重复这个过程若干遍，取最小值即可。

考虑若已经知道了最终的一条最优路径，其上最多有 \(K\) 个点，\(k\) 个点再一种染色方案中黑白相间的概率是 \(\frac{1}{{{2} ^ {k}} - 1}\)，随机 \(5000\) 次，随不出正确答案的概率为 \({{(\frac{511}{512})} ^ {5000}} \approx {0.000056845461206}\)，非常小，可以忽略不计。

Reflect

遇到奇环可以往二分图黑白染色想；

随机化的话，观察性质算概率吧，若数据很小，随机化次数多的话概率就越低。

T3 P3203 [HNOI2010] 弹飞绵羊~

题意

有 \(n\) 个装置，每个装置设定初始弹力系数 \(k_i\)，当绵羊达到第 \(i\) 个装置时，它会往后弹 \(k_i\) 步，达到第 \(i+k_i\) 个装置，若不存在第 \(i+k_i\) 个装置，则绵羊被弹飞。

有 \(m\) 次操作：

若 \(op=1\)，求从编号为 \(x\) 的装置出发被弹飞的次数。
若 \(op=2\)，将编号为 \(x\) 的弹力装置的系数修改成 \(k\)。

\({1} \le {n} \le {{2} \times {{10} ^ {5}}},{1} \le {m} \le {{10} ^ {5}}\)

Solution

经典的分块题（正解是 LCT）。

对位置分块，考虑维护每个块内的信息，对于每个位置 \(i\)，维护 \(stp_i,to_i\) 分别表示从 \(i\) 跳出该块的右端点的次数，其跳出所属的块后到达的位置。

块与块直接相互独立，查询时暴力跳，修改时直接对整个块重构即可，时间复杂度为 \(O(n\sqrt{n})\)。

T4 P4383 [八省联考 2018] 林克卡特树*

10/23

已经到霜降了？？？

T1 P4552 [Poetize6] IncDec Sequence

题意

给定一个长度为 \(n\) 的数列 \(a\)，每次可以选择一个区间 \([l,r]\)，使这个区间内的数都加 \(1\) 或者都减 \(1\)。

求能使数列中的所有数都一样的最小次数，并求出在保证最少次数的前提下，最终得到的不同数列的种数。

\({1} \le {n} \le {{10} ^ {5}},{0} \le {a_i} \le {{2} ^ {31}}\)

Solution

利用差分思想，对区间 \([l,r]\) 加 \(1\) 或者减 \(1\)，其实就是对差分数组 \(b\) 中的 \(l\) 加 \(1\)，\(r + 1\) 减 \(1\)；或者反过来。

使得所有数都一样，也就是 \(\forall {{i} \in {(1,n]}},{b_i = 0}\)，分类讨论：

选取一对满足 \({b_x} > {0},{b_y} < {0}\) 的数对 \((x,y)\)，对 \(x\) 减 \(1\)，对 \(y\) 加 \(1\)，必然可以将绝对值小的一方归零，代价为 \(\min{\{|x|,|y|\}}\)。
选取一个满足 \(b_x > 0\) 的 \(x\)，让其与 \(b_1\) 配对，代价为 \(|x|\)。
选取一个满足 \(b_y < 0\) 的 \(y\)，让其与 \(b_{n + 1}\) 配对，代价为 \(|y|\)。

综上可知：

\[Ans = \min{\{|x|,|y|\}} + |x - y| = \max{\{|x|,|y|\}} \]

求合法的解数，明显和 \(b_1\) 有关，容易推出为 \(|x - y| + 1\)。

时间复杂度为 \(O(n)\)。

Reflect

很套路了，区间同时加减可以用差分啊！！！

T2 P2403 [SDOI2010] 所驼门王的宝藏~

题意

有一个 \({r} \times {c}\) 的矩阵，有 \(n\) 个格子有零食，每一个有零食的格子都有一种类型的传送门：

横天门：由该门可以传送到同行的任一格子；
纵寰门：由该门可以传送到同列的任一格子；
任意门：由该门可以传送到以该门所在格子为中心周围 \(8\) 格中任一格子（如果目标格子存在的话）。

不限起始位置，最大化经过有零食的格子数量。

\({1} \le {n} \le {{10} ^ {5}},{1} \le {r,c} \le {{10} ^ {6}}\)

Solution

发现边是有向的，若已经建好图，很套路的缩点再对 DAG 做 dp。

问题在于如何建图，如果有一行全是横天门或者有一列全是纵寰门，连个格子之间暴力建图，已经到了 \(O(n^2)\) 级别的。

考虑对每一行和每一列都新建立一个节点（可以看作有横天门或者纵寰门的格子前往其他格子的中转站），每个有零食的格子都可以被该行/列的新节点连边，如果该格子上有横天门，则可以往该行的节点在连一条边；纵寰门同理。

对于任意门，直接对可以到达有零食的点连边即可。边的数量是线性的。

Reflect

考场上有一个类似的想法，对每一行的所有相邻有横天门的格子连边；每一列同理，任意门直接连有零食的格子。应该可行？？？

最短路可以往 dijkstra 上想，本题类型可以看做最长路问题，一般只能用 DAG 上 dp 或者矩阵快速幂解决。

T3 CF710F String Set Queries~

题意

维护一个字符串集合 \(S\)，支持 \(m\) 次以下操作之一：

加入字符串；
删除字符串；
查询集合中所有字符串在给出的模版出现的次数。

强制在线。

\({1} \le {m} \le {{3} \times {{10} ^ {5}}},\sum{|s|} \le {{3} \times {{10} ^ {5}}}\)

Solution

很好的一道题，做法很多qwq

下文令 \(n = \sum{|s|}\)，并将 \(n,m\) 看成同阶。

先将好实现的根号做法：

暴力查询直接枚举模式串中所有子串，并记录出现次数，用哈希维护。复杂度为 \(O(n^2)\)。

优化非常简单，只枚举集合中的字符串的长度作为子串的长度，复杂度为 \(O(n\sqrt{n})\)，用 set 或者 map 维护即可。

证明：最坏情况下，集合中字符串的长度各不相同，长度为 \(1,2,3,\ldots,k\)，\({\sum_{i=1}^{k}{i}} \le {n}\)，因此 \({t} \le {\sqrt{2n}}\)，最多只会有 \(\sqrt{2n}\) 个不同的长度。

另一种正常的做法：二进制分组 + AC 自动机（ACAM）。

二进制分组：把所有的操作按二进制分组，每一组里面就开个数据结构维护，属于在线算法。

假设已经分好两组，每组的大小分别为 \(\{4,2\}\)（大小就是里面包含的操作个数），加一个操作，那么就有三组 \(\{4,2,1\}\)；再加一个操作就是 \(\{4,2,1,1\}\)。
暴力重构，\({\{4,2,1,1\}} \to {\{4,2,2\}} \to {\{4,4\}} \to {\{8\}}\)。
可以得到，若有 \(m\) 个操作，至多会分为 \(\log{m}\) 组；暴力重构的过程中，每个点至多被重构 \(\log{m}\) 次，再乘上数据结构维护对应的复杂度就是重构的复杂度了。

对于插入操作，二进制分组，每组建一个 ACAM；查询的时候对 \(\log{m}\) 个 ACAM 都扫一遍即可。

对于删除操作，发现贡献具有 可减性，即求出所有串的贡献，减去已删除串的贡献，就是当前剩下来的串的贡献。

因此只要对插入、删除的字符串分别进行二进制分组，再相减即可。

ACAM 的建树是 \(O(n)\) 的，插入时每个串最多被重构了 \(\log{m}\) 次 fail 指针，所以插入复杂度是 \(O(n\log{m})\)，查询是 \(O(n\log{m})\) 的。

总时间复杂度是 \(O(n\log{m})\)，带一个 \(26\) 的常数。

有时间回来补第二种做法！！！

Reflect

新想法：二进制分组

多想想 ACAM 好不好qwq

对于字符串模式匹配的题现在可以多一种往根号复杂度思考的想法了。

闲话

早知道多看看这题了，2025 CSP-S2 T3 其实也可以用本题的思想啊啊啊！！！

T4 CF1810G The Maximum Prefixs

题意

有一个长度为 \(n\) 的数组 \(a\)，其中每个 \(a_{i}\) 的取值为 \(1\) 或 \(-1\)。

按照如下方式生成该数组：

首先，选择一个整数 \(k\)，决定数组 \(a\) 的长度。
然后，对于每个 \(i\)，以概率 \(p_{i}\) 令 \(a_{i} = 1\)；否则以概率 \(1 - p_{i}\) 令 \(a_{i} = -1\)。

令 \(s_{i} = \displaystyle \sum_{j=1}^{i}{a_{j}}\)，特别地，\(s_{0} = 0\)。然后令 \(S = \displaystyle \max_{i=0}^{k}{s_{i}}\)，即 \(S\) 是数组 \(a\) 的最大前缀和。

给定 \(n+1\) 个整数 \(h_{0}, h_{1}, \ldots, h_{n}\)。对于最大前缀和为 \(S\) 的数组 \(a\)，其得分为 \(h_{S}\)。

对于每个 \({k} \in {[1,n]}\)，求长度为 \(k\) 的数组的期望得分。

\({1} \le {n} \le {5000}\)

Solution

钦定数组 \(a\) 的最大前缀和为 \(x\)，那么前缀和数组 \(s\) 需要满足：

\(\forall {{i} \in {[0,n]}},{{s_i} \le {x}}\)
\(\exists {{i} \in {[0,n]}},{{s_i} = {x}}\)

形象地，钦定这个最大前缀合 \(x\) 为“目标”。

令 \(f_{i,j,0/1}\)，表示仅考虑前 \(i\) 个元素，当前前缀和 \(s_i\) 离目标还差 \(j\)，之前是/否达到过目标的期望得分。

初始化 \(f_{0,i,[i=0]} = h_i\)，有转移：

\[f_{i,j,l|[j=0]} = {f_{i-1,j+1,l}} \times {p_i} + {f_{i-1,j-1,l}} \times {(1 - p_i)} \]

长度为 \(k\) 的期望值为 \(\displaystyle \sum_{i=0}^{n}{f_{k,i,1}}\)，时间复杂度为 \(O(n^2)\)。

10/24

魔方破了一次 PB（使用“魔域文化”）：

跳步（第三步）：\(19.66s\)

首次突破 \(20s\)

时间：\(9:30\)，地点：科学楼 \(5\) 楼大天台靠珠江的一边（大风），音乐：无人知晓的我

当时我挑战两次速拧，第一次 cjr 没停表，但是说好像是 \(22''\)（不跳步），啊啊啊，没记录的 PB qwq

后面拧出了不跳步 \(23.85s\)，有记录到的新 PB ！！！

然后 \(24.46s\)（不跳步），目前第二快记录。

时间：\(13:00\)，地点：宿舍 621，音乐：无人知晓的我

T1 P3611 [USACO17JAN] Cow Dance Show S

题意

给定一个长度为 \(n\) 的序列 \(d\)，\(d_i\) 表示第 \(i\) 头奶牛的表演持续的时间，表演完后就会下场；再给定一个正整数 \(k\)，表示一个时刻最多能容纳 \(k\) 头奶牛表演。

奶牛按照编号依次上场，当最后一头奶牛表演结束，用了 \(t\) 个单位时间。

显然，\(k\) 的值越大，\(t\) 就越小。给定 \(t\) 的最大可能值的上限 \(t_{max}\)，求在这个约束下 \(k\) 的最小值。

\({1} \le {n} \le {{10} ^ 4},{t_{max}} \le {{10} ^ {6}},{1} \le {d_i} \le {{10} ^ {5}}\)

Solution

很显然能想到二分答案 \(x\)，最多能容纳 \(x\) 头奶牛同时表演，用优先队列（小根堆）维护当前还在表演的奶牛，记录总时间再判定即可。

时间复杂度为 \(O(n\log^2{n})\)。

T2 P4137 Rmq Problem / mex~

题意

有一个长度为 \(n\) 的数组 \(\{a_1,a_2,\ldots,a_n\}\)。

\(m\) 次询问，每次询问一个区间内最小没有出现过的自然数。

\({1} \le {n,m} \le {{2} \times {{10} ^ {5}}},{0} \le {a_i} \le {{10} ^ {5}}\)

Solution

一个数 \(x\) 在区间 \([l,r]\) 没出现过，要么 \(x\) 没出现过，要么在 \(r\) 前出现的位置 \(< {l}\)，考虑维护每个数当前最后出现的位置，没出现过赋为 \(0\)。

可持久化权值线段树维护 \(minx\) 表示当前区间内的元素最后出现位置的最小值。查询时对位置 \(r\) 上的版本做线段树上二分找最左边的 \(< l\) 的位置，就是区间的 \(\mathbb{mex}\)。时间复杂度为 \(O(n\log{V})\)。

初中时的做法：莫队+值域分块。

先把所有询问离线下来，排序跑莫队：

插入和删除一个数时，分别对该数出现次数 \(cnt\) 和其所属的块出现元素个数 \(sum\) 更新；
查询时从左向右暴力遍历所有块，找到第一个满足 \({sum_i} < {b}\)（其中 \(b\) 为块长）的块 \(i\)，再对块内查询第一个 \(cnt_j = 0\) 的数 \(j\) 即可。

时间复杂度为 \(O(n\sqrt{V})\)。

Reflect

小技巧：计数或者找区间的某些特定的数时，记录每个数最后出现的位置会有很多好性质。

T3 P7842 「C.E.L.U-03」探险者笔记 III~*

T4 CF455D Serega and Fun

题意

给定长度为 \(n\) 的序列 \(a\)，有 \(q\) 次操作：

1 l r：将区间 \([l,r]\) 依次向右移动一位，其中 \(a_r\) 移动到 \(a_l\)。
2 l r k：询问区间 \([l,r]\) 中 \(k\) 出现的次数。

强制在线。

\({1} \le {n,q} \le {{10} ^ {5}},{1} \le {a_i} \le {n}\)

Solution

考虑对序列 \(a\) 的位置分块，对于每个块维护一个队列（先进先出的性质很适合本题）或者双端队列，来支持右移操作。

同时维护一个桶，记录每个块内不同元素出现的次数，便于查询。

操作 1 时特殊处理左右残块，由于队列无法直接访问中间位置的数，需要把左右块队列中的所有数拿出来，右移完再入队；

操作 2 查询时类似，取出来暴力计数即可。

注意细节处理，时间复杂度为 \(O(n\sqrt{n})\)。

Reflect

对区间动态滚动的操作不妨考虑队列的先进先出性质。

分块不乏成为一个很好的工具。

10/25

周六中午开完家长会，被父母接出去吃了餐午饭，又会校，好消息是终于登上 B 站了。

T1 P10849 [EGOI 2024] Bike Parking / 车位分配

题意

有一个停车场，停车位有 \(n\) 个不同的等级，级别为 \(t\) 的停车位数量为 \(x_t\)，级别越小，停车位等级越高。

给定每个等级 \(s\) 的停车位的订阅个数 \(y_s\)。

如果订阅等级为 \(s\) 的用户被分配到级别 \(t\) 的停车位，那么会发生以下三种情况之一：

如果 \(t < s\)，用户会感到高兴，并会为应用点赞。
如果 \(t = s\)，用户会感到满意，不会有任何反应。
如果 \(t > s\)，用户会感到生气，并会给应用差评。

设 \(u\) 为点赞数，\(d\) 为差评数。通过最佳分配用户到停车位使得最大化 \(u - d\)。

\({1} \le {n} \le {{3} \times {{10} ^ {5}}},{0} \le {x_i,y_i} \le {{10} ^ {9}}\)，保证停车位足够。

Solution

其实就是田忌赛马问题？？？初赛时好像还总结过。

简单的想，能点赞就点赞，若还剩停车位，剩下的人就补上去。

若停车位已经满了，接下来思考几个分配：

将没有任何反应的用户换到等级更高的车位，换上去的用户会点赞，而换下来的用户会给差评，一抵消，相比原来的分配不劣；若换下来的用户本来给的就是差评，则可能更优。
将差评的用户和没反应的用户互换，则差评的用户变成了点赞，没有反应的用户变成会给差评，一抵消，相当于没有任何反应，相较于原来的分配（必然有差评）更优。

综上，能得出来一个小结论：当前订阅等级为 \(i\) 的用户若能去等级更高 \(j < i\) 的停车位就直接去，不劣。

有点反悔贪心的思想。从等级高的停车位开始依次考虑，令 \(sum\) 为前面还剩的空停车位，贪心地，必然是能停就停，加上贡献；\(cnt\) 为前面 \(t = s\) 的停车位，按照刚刚得出的结论，也是能换就换。

剩下不能去更高等级的用户，只能放在当前或者后面的停车位，比较大小判断计算贡献即可。

T2 P9310 [EGOI 2021] Luna likes Love / 卢娜爱磕 cp

题意

给定一个长度为 \(2n\) 的序列 \(a\)，\(a_i\) 为 \({1} \sim {n}\) 的整数。其中，每个整数出现且仅出现两次。

可以进行两种操作：

交换两个相邻的数的位置。
删除两个相邻且相同的数。

最后要使序列为空，求最少进行的操作数。

\({1} \le {n} \le {{5} \times {{10} ^ {5}}},{1} \le {a_i} \le {n}\)

Solution

脑电波题？？？

感觉有点贪心，当前的序列相邻两个有相等就直接拿走。

不妨设相同的数出现的位置分别为 \([l,r]\)，考虑两对元素 \([l_1,r_1]\) 和 \([l_2,r_2]\)（这里钦定 \({l_1} < {l_2}\)）：

完全不相交，即 \({l_1} < {r_1} < {l_2} < {r_2}\)：没必要考虑互相之间的影响，哪一对先消掉都是一样的。
包含关系，即 \({l_1} < {l_2} < {r_2} < {r_1}\)：先让靠里的元素对先消掉，这样靠外的元素对就可以少交换两次。
部分相交，即 \({l_1} < {l_2} < {r_1} < {r_2}\)：发现先消掉哪一边都一样。

综上，发现有些交换是必要的，存在于非包含区间的相交中，那么对所有区间排序，利用扫描线的思想，树状数组维护即可，时间复杂度为 \(O(n\log{n})\)。

Reflect

做出来了，其实没有想到怎么严格证明正确性。

对于区间的问题，可以通过包含，相交等关系考察性质。

T3 P3573 [POI 2014] RAJ-Rally

题意

给定一个 \(n\) 个点 \(m\) 条边的有向无环图，每条边长度都是 \(1\)。

找到一个点，使得删掉这个点后剩余的图中的最长路径最短。

\({2} \le {n} \le {{5} \times {{10} ^ {5}}},{1} \le {m} \le {{10} ^ {6}}\)

Solution

由于是 DAG，不妨先拓扑排序，并 \(O(n)\) 求出 \(dis_{i,0/1}\) 分别为以 \(i\) 为终点/起点的最长路。

经过边 \({u} \to {v}\) 的最长路为 \(dis_{u,0} + 1 + dis_{v,1}\)。

将拓扑序小于 \(i\) 的节点集合记为 \(A\)，大于 \(i\) 的节点集合记为 \(B\)，删去 \(i\) 后，最长路的路径可能为：

\({A} \to {A}\)
\({A} \to {B}\)
\({B} \to {B}\)

因此我们需要维护 \(dis_{u,0}({u} \in {A}),dis_{v,1}({v} \in {B})\) 和 \(dis_{u,0} + 1 + dis_{v,1}({u} \to {v})\)。

考虑转移的过程（注：以下图片都选取自 LuoGu 的本题题解中）：

原本数据结构中有 \(dis_{\{1,2,3\},0},dis_{\{4,5,6\},1},dis_{2,0} + 1 + dis_{4,1},dis_{3,0} + 1 + dis_{5,1}\)。

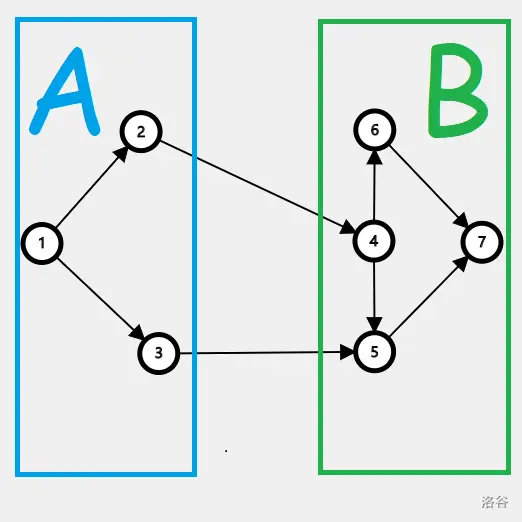
P3573_1

从集合 \(B\) 中删除节点 \(4\)，在数据结构中删除 \(dis_{4,1},dis_{2,0} + 1 + dis_{4,1}\)，此时其中的最大值就是删除点 \(4\) 的最大值。

P3573_2

将节点 \(4\) 加入集合 \(A\) 中，在数据结构中加入 \(dis_{4,0},dis_{4,0} + 1 + dis_{6,1},dis_{4,0} + 1 + dis_{5,1}\)，转移到下一个状态。

P3573_3

初始时所有节点都在集合 \(B\)，然后按照拓扑序依次加入集合 \(A\)。

由于普通的堆不能直接随机取值删除，则用手写 可删堆 支持插入、删除、求最大值的操作。还可以用 multiset 和权值线段树维护。

可删堆：

struct Queue {
    priority_queue<int> a,b;
	int cnt;
    inline void Push(int x) {
        a.push(x);
		cnt++;
    }
    inline void Pop(int x) {
        b.push(x);
		cnt--;
    }
    inline int Top() {
        while(!b.empty()&&a.top()==b.top())
            a.pop(),b.pop();
		if(!cnt) return -inf;
		return a.top();
    }
} Q;

初始化和拓扑排序为 \(O(n+m)\)，每个点和边都加入和删除过一次，总复杂度为 \(O((n+m)\log{(n+m)})\)。

Reflect

DAG 想到拓扑排序，利用拓扑序和预处理，发现点之间可以简单用数据结构维护转移。

遇到拓扑序，其实可以多枚举点 \(i\)，把点 \(i\) 前后分成两部分讨论。

T4 P6811 「MCOI-02」Build Battle 建筑大师~^

10/26

留校养状态，其实也没什么心思学习qwq浅学了一下。

10/27

\(22.72s\) 不跳步，目前有记录的第二快。

音乐：silver city，时间：\(18:10\)，地点：科学楼 \(5\) 楼天台中央

T1 CF250B Restoring IPv6

题意

给定 \(n\) 个简写格式的 IPv6 地址，还原成完整格式。

\({1} \le {n} \le {100}\)

Solution

小模拟，简单想一下如何计算 :: 产生 0000 的个数，并将所有块的前导 0 补上即可。

T2 P11791 [JOI 2017 Final] 准高速电车 / Semiexpress

题意

在某条铁路沿线共有 \(n\) 个站点，依次编号为 \(1,2,\ldots, n\)。当前有两种列车服役，分别是高速列车和普通列车。

普通列车每站都停，对于每一个 \(i\)，从站点 \(i\) 到站点 \(i+1\) 用时 \(a\) 分钟。
高速列车只在站点 \(s_1,s_2,\ldots,s_m\) 停车，对于每一个 \(i\)，从站点 \(i\) 到站点 \(i+1\) 用时 \(b\) 分钟。

铁路公司拟定开设第三类车次：准高速列车。对于每一个 \(i\)，从站点 \(i\) 到站点 \(i+1\) 用时 \(c\) 分钟。准高速列车停的站点还没有决定好，但是这些站点必须满足以下要求：

高速列车停的所有站点准高速列车都必须停。
准高速列车必须停恰好 \(k\) 个站点。

合理地安排准高速列车停的站点，最大化从 \(1\) 号站点出发在 \(t\) 分钟内抵达的站点（\(1\) 号站点不计，不计等车和换乘时间）数目。

\({2} \le {n} \le {{10} ^ {9}},{2} \le {m} \le{k} \le {3000},{k} \le {n}\)

\({1} < {b} < {c} < {a} \le {{10} ^ {9}}\)

\({1} = {s_1} < {s_2} < \ldots < {s_m} = {n}\)

Solution

由于 \({b} < {c} < {a}\)，所以对于 \({i} \in {[1,m]}\) 的站点 \(s_i\)，直接做高速列车时最快的。进而把问题拆分成了两个高速列车站点的子问题。

考虑如何安排准高速列车的站点：

显然是在第一个普通列车不能能到到的站点设立一个准高速列车是最优的。

先假定 \(k\) 足够大的情况下，暴力记录 \(s_{i}\) 到 \(s_{i+1}\) 之间的所有可能得准高速列车站点。

但是 \(k\) 是有限制的，发现每个准高速列车站点对总数目的贡献是不一样的，不妨把所有准高速列车站点拎出来，取贡献最大的那 \(k\) 个，用优先队列维护贡献。

\(n\) 比较大，暴力跑完 \(s_{i}\) 到 \(s_{i+1}\) 是不可行的，考虑优化：

对于 \(s_{i}\) 与 \(s_{i+1}\) 之间，最多遍历前 \(k\) 个可能的准高速列车站点；
同时记录队列的大小 \(tot\)，若 \({tot} > {k}\)，则将队列中最劣的站点扔掉，由于站点越前，贡献必然更大，所以能保证扔掉的站点不影响站点的连贯性。

最后将优先队列中所有贡献相加即可，时间复杂度为 \(O(mk+k\log{k})\)。

Reflect

发现每个站点之间相互独立，且后面的站点必然比前面的站点劣，扔掉不影响连贯性的关键性质，以此做到优化。

提一嘴，优先队列结构体的自定义排序：

struct Node {
    int val,ty;
    bool operator < (const Node &y)const {
        if(ty!=y.ty)
            return ty>y.ty;
        return val>y.val;
    }
};
priority_queue<Node> q;

实现的是先对 \(val\) 从小到大，再对 \(ty\) 从小到大。

T3 P4434 [COCI 2017/2018 #2] Usmjerie~

题意

给定一棵 \(n\) 个点的树，初始时边为无向边，现在需要将所有的边改为有向边（不允许双向连通），给出 \(m\) 条限制 \((x_i,y_i)\)，要求将所有边改为有向边后，使得从 \(x_i\) 可以到达 \(y_i\)，求修改的方案数。

\({1} \le {n,m} \le {{3} \times {{10} ^ {5}}}\)

Solution

把 \(1\) 定为树根，用 \(0/1\) 分别表示每条边指向父亲/儿子。

转化 \(m\) 条限制，令 \(z = lca(x,y)\)：

\({x} \to {z},{y} \to {z}\) 的整条路径上都分别为 \({1,0}\) 或者 \({0,1}\)。

将 \(u\) 和其父亲相连的边的边权记录到 \(u\) 上（边权转点权）。

令 \(son_x\) 表示 \(z\) 往 \(x\) 跳一步走到的点；\(son_y\) 同理：

\(x\) 到 \(son_x\) 路径上的点权相同
\(y\) 到 \(son_y\) 路径上的点权相同
若 \(x\) 和 \(y\) 都不为 \(z\)，则 \(x\) 和 \(y\) 的点权不同

对于限制 \(1,2\)，每次合并树上的一条祖先链，连通块内相同；在 \(x\) 和 \(son_x\) 上打上标记，再做树上差分，若一个点有至少一个标记，则和其父亲合并，这里可以用并查集维护。

（下图是一种矛盾的情况，其中粉色圈的地方有向边冲突了）

P4434

考虑限制 \(3\)，若 \(x,y\) 已经在一个连通块上，则矛盾无解；否则用一条边连接两个点所在的连通块。

把连通块缩点，得到一个无向图，有解的条件必然是改图可以黑白染色。

记连通块的数量为 \(cnt\)，则方案数为 \({2} ^ {cnt}\)，因为单独连通块内方向固定，只有两种方案。

并查集合并的复杂度为 \(O(n\alpha{(n)})\)，树剖 LCA 的复杂度为 \(O(n\log{n})\)，总时间复杂度为 \(O(n\alpha{(n)} + n\log{n})\)。

Reflect

类似于两点由 LCA 分成两边相反，且判定合法时，可以想到先用并查集合并同类条件，再用黑白染色。

多转化限制或者条件（可以用拆解、分类等方法），多观察多个有交的路径上的边的方向必须相同关系的性质。

T4 P11666 [JOI 2025 Final] 邮局 / Post Office*

10/28

T1 AT_abc200_e [ABC200E] Patisserie ABC 2

题意

对于所有的 \({1} \le {i,j,k} \le {n}\) 且 \({i} \ne {j} \ne {k}\) 组成的 \({{n} ^ {3}}\) 个三元组，按照总和为第一关键字，\(i\) 为第二关键字，\(j\) 为第三关键字从小到大排序。

求从左到右排在第 \(K\) 位的元素的 \((i,j,k)\)。

\({1} \le {n} \le {{10} ^ {6}},{1} \le {K} \le {{n} ^ {3}}\)

Solution

对于总和为 \(s\) 的三元组，尝试计算其个数，转化一下：

求 \(i + j + k = s\) 且 \({i,j,k} \le {n}\) 的 \((i,j,k)\) 的方案数。

先抛开后面的限制，那就是插板法，对 \(s - 1\) 个空隙插 \(2\) 个板，即 \(\binom{s-1}{2}\)。

考虑如何去掉不合法的情况，就是存在 \(> {n}\) 的数的情况，很显然用容斥原理：

\[\binom{s-1}{2} - \binom{s-n-1}{2} + \binom{s-2n-1}{2} \]

找到第 \(K\) 位三元组属于的总和 \(s\)，再枚举 \(i\)，算出 \(j\) 的上下界 \(u,d\)，逐位比较排名，以此确定 \(i\)，同时也得到了 \(j\)，最后 \(k = s - i - j\)。

由于 \(K\) 不断变小，所以时间复杂度是线性的。

Reflect

确定某一排名的数对时，尝试用逐位确定，先确定前几位，再枚举后面的位，一般要用到上下界，由于排名不断减小，必然线性。

多转化题意，遇到计数题，插板法、插空法等排列组合技巧必须牢记。

T2 P7150 [USACO20DEC] Stuck in a Rut S

题意

在二维坐标系上有 \(n\) 头奶牛 \((x_i,y_i)\)，共有两类奶牛，一种向上走，一种向右走，但当一头奶牛走到另一头奶牛走过的地方时，会停止移动，求每只奶牛阻挡的奶牛数量（阻挡具有传递性）。

注意若两头奶牛同时走到一个点，互相不会阻挡，继续前进。

\({1} \le {n} \le {1000},{1} \le {x_i,y_i} \le {{10} ^ {9}}\)

Solution

如果不会被阻挡，每头奶牛走过的路径是条射线，考虑把所有射线的交点记录下来，这些交点有可能成为某头奶牛停止移动的位置。

对于一个交点 \((p,q)\) 上的两头奶牛 \(i,j\)，后到的奶牛 \(j\) 必然被阻挡，必要条件是 \({|x_i - p| + |y_i - q|} < {|x_j - p| + |y_j - q|}\)。

记 \(cnt_i\) 表示奶牛 \(i\) 当前阻挡的奶牛的个数。

则 \({cnt_i} \gets {cnt_i + cnt_j + 1}\)，再给 \(j\) 打上删除标记，进而 \(j\) 后面的交点也不复存在。

唯一的问题在于判断交点的顺序。

由于奶牛只可能往右和往上走，所以先遍历左下角的交点必然是最先的。

时间复杂度为 \(O(n^2\log{n^2})\)，瓶颈在对交点顺序进行排序。

Reflect

遇到有时间限制的计数时，有时候可以先想没有限制、无限走下去的状态，再按限制约束的发生顺序处理，对于后面不可能发生的情况，设定一个删除数组标记就可以了。

T3 P8162 [JOI 2022 Final] 让我们赢得选举 / Let's Win the Election*

T4 P13342 [EGOI 2025] Wind Turbines / 风力涡轮机~*

10/29

可惜去不了体艺节开幕式，有幸参加了晚上的班级展演，自我感觉第一天的晚会不错，我的库里神歌出现了，好评。

T1 P11104 [ROI 2023] 监控 (Day 1)

题意

有一个 \({h} \times {w}\) 的矩阵，可以选择对其进行上、下、左、右的移动。

给定有 \(k\) 个被染黑的格子 \((x_i,y_i)\)，最小化移动步数使得包含全部黑格子的矩形的面积尽量小。

移动规则：

上：将每一行上移一位，第一行移至最后一行。
下：将每一行下移一位，最后一行移至第一行。
左：将每一列左移一位，第一列移至最后一列。
右：将每一列右移一位，最后一列移至第一列。

\({1} \le {h,w} \le {{10} ^ {9}},{1} \le {k} \le {{10} ^ {5}}\)

Solution

上下移动，左右移动相互独立，分别计算最优方案。

对于上下移动，重点在于第一行和最后一行的位置，且只要这两行的排位不变，如何移动都不改变两行的绝对距离。

枚举当前第一行，计算其对行数贡献，判断上下移动的优先级（看移动距离大小），按照行数贡献为第一关键字，移动距离为第二关键字，对所有行比较即可。

左右移动同理，最后矩形的最小面积就是行的最小值乘上列的最小值，总移动距离也是两值相加。时间复杂度为 \(O(k)\)。

T2 CF2025E Card Game

题意

定义两个二元组 \((a,b)\) 与 \((c,d)\) 满足 \({(a,b)} > {(c,d)}\) 当且仅当：

\({a} = {1}\) 且 \({c} \ne {1}\)
\({a} = {c}\) 且 \({b} > {d}\)

有 \({n} \times {m}\) 个二元组 \((x,y)\)，其中 \({x} \in {[1,n]},{y} \in {[1,m]}\) 且二元组没有重复。

需要将这 \({n} \times {m}\) 个二元组均分配给左右双方，左方能战胜右方当且仅当能够把双方的二元组两两匹配，每个匹配中左方的二元组都大于右方的二元组。

求左方能够打败右方的二元组分配方案数。

\({1} \le {n,m} \le {500}\)

Solution

发现 \(x = 1\) 的二元组是特殊的，能大于所有 \({x} \ne {1}\) 的二元组，所以不妨单独拎出来讨论。

对于 \({x} \ne {1}\) 的二元组，考虑同一个 \(x\) 内的二元组 \((x,y)\) 如何匹配。

\(g_{i,j}\) 表示前 \(i\) 个 \(x\) 相同且 \({y} \le {i}\) 的二元组 \((x,y)\)，左方选了其中 \(j\) 个的合法分配方案数。

初始化 \(g_{0,0} = 1\)，显然要保证 \({2j} \le {i}\)，有转移：

当 \(x\) 相同时，第 \(i\) 个二元组必然是当前最大的，左方直接选，前提条件是 \({j} > {0}\)，有：

\[g_{i,j} \gets {g_{i,j} + g_{i-1,j-1}} \]

左方不选，前提条件是 \({2j} < {i}\)，有：

\[g_{i,j} \gets {g_{i,j} + g_{i-1,j}} \]

\(f_{i,j}\) 表示考虑完 \({x} \in {[2,i]},{y} \in {[1,m]}\) 的所有二元组 \((x,y)\)，还剩 \(j\) 的 \(x = 1\) 的二元组的合法分配方案数。

显然的，初始化为 \(f_{1,i} = g_{m,\frac{m-i}{2}}\)，这里 \(i\) 为偶数。

记左方选了 \(z\) 个 \(x = i\) 的二元组，那么剩下的 \(m - 2z\) 个二元组被右方拿走，这些二元组只能和 \(x = 1\) 的二元组去匹配。

枚举 \(k = m - 2z\)，保证 \({j + k} \le {m}\) 且 \(m - k\) 为偶数，有转移：

\[f_{i,j} = \sum_{k}{{f_{i-1,j + k}} \times {g_{m,\frac{m-k}{2}}}} \]

最终左方能够打败右方的二元组分配方案数为 \(f_{n,0}\)。

时间复杂度为 \(O(n^3)\)。

Reflect

在想转移方程式时，多注意边界条件。

想到奇特的转移方程时也不要犹豫，推出来意义是对的就去打！！！

T3 P10226 [COCI 2023/2024 #3] Restorani*

T4 P12033 [USACO25OPEN] Package Pickup P*

10/30

体艺节，爽逃一早上，下午回机房做了几题，晚上全班都能去看文艺晚会。

晚会氛围特别好，特别爽，开心。

\(18:00\) 左右开始挑战。

在宿舍。

（音乐）淋一场雨：

连续达成 \(25.73s,24.71s,23.93s\)，都不跳步。

（音乐）silver city：

达成 \(23.10s\)，跳倒数第 \(2\) 步。

（音乐）GO学长的小曲：

达成 \(20.75s\)，跳倒数第 \(2\) 步。

晚上继续：

（音乐）淋一场雨：

\(22:20\)，连续达成 \(23.87s\)（不跳步）和 \(23.00s\)（跳倒数第 \(2\) 步）

T1 AT_abc393_d [ABC393D] Swap to Gather

题意

给定一个长度为 \(n\) 的 01 字符串 \(s\)，可以花费 \(1\) 代价交换相邻两个字符。

求将所有字符 1 变成一段连续的子串的最小代价。

\({2} \le {n} \le {{5} \times {{10} ^ {5}}}\)

Solution

利用前缀和 \(sum_i,cnt_i\) 分别维护 \([1,i]\) 中所有 1 的位置和 1 出现的次数。

枚举两边向中间集中的位置 \(i\)，利用等差数列求和，得到移动距离为：

\[{({cnt_{i-1}} \times {i} - sum_{i-1})} + {[(sum_n - sum_i) - {i} \times {(cnt_n - cnt_i)}]} - {\frac{{(cnt_{i-1} + 1)} \times {cnt_{i-1}}}{2}} - {\frac{{[(cnt_n - cnt_i) + 1]} \times {(cnt_n - cnt_i)}}{2}} \]

（可以理解成全部都到 \(i\)，再左右依次排列）

对所有情况取最小值即可，时间复杂度为 \(O(n)\)。

T2 P10761 [BalticOI 2024] Trains

题意

定义 \(f(u,v)\) 表示从 \(u\) 走到 \(v\) 的走法的方案数。

给定 \(n\) 辆火车，第 \(i\) 辆火车从站点 \(i\) 出发，每 \(d_i\) 站停一次，共停 \(x_i\) 站。

求 \(\displaystyle \sum_{i=1}^{n}{f(1,i)}\)。

\({1} \le {n} \le {{10} ^ {5}},{0} \le {d_i,x_i} \le {{10} ^ {9}}\)

Solution

先考虑暴力 dp，\(f_i\) 表示到达 \(i\) 为终点的方案数。枚举 \({j} \in {[1,x_i]}\) 有转移：

\[{f_i} \to {f_{i + {j} \times {d_i}}} \]

时间复杂度为 \(O(n^2)\) 的。

隔一段加一个的操作显然并不好直接用数据结构维护。“一段一段”？想到了根号分治，令 \(b = \sqrt{n}\)，对于已经有的铁路线：

对于 \({d_i} > {b}\) 的情况，如上面的直接转移就可以了，每次转移是 \(O(\sqrt{n})\) 的。
对于 \({d_i} \le {b}\) 的情况，则不同的 \(d\) 最多只有 \(\sqrt{n}\) 种；\(g_{i,j}\) 表示最后由一个 \(d = j\) 的铁路线到达 \(i\) 的方案数，得到一部分的转移：
- 将这条 \(d = j\) 的铁路继续往下一个站点开，\({g_{i+j,j}} \gets {g_{i+j,j} + g_{i,j}}\)。

将 \(f,g\) 的贡献合并：\({f_i} \gets {f_i + \sum_{i=1}^{b}{g_{i,j}}}\)。

更新完从前面的站点出发到站点 \(i\) 的状态 \(f_i,g_{i,j}\)。

新增一个新的铁路线 \((d,x)\)：

若 \({d} \le {b}\)，利用类似于差分的思想：
- 线路开通：\({g_{i+d,d}} \gets {g_{i+d,d} + f_i}\)
- 最多到第 \(x\) 站：\({g_{{i}+{(x+1)}\times{d},d}} \gets {g_{{i}+{(x+1)}\times{d},d} - f_i}\)
若 \({d} > {b}\)，直接对后面可能到达的站点转移：
- \(\forall{{k} \in {[1,x]}},{f_{i+{k}\times{d}}} \gets {f_{i+{k}\times{d}} + f_i}\)

总方案数为 \(\displaystyle \sum_{i=1}^{n}{f_i}\)。

\(f_i\) 的转移是 \(O(\sqrt{n})\)，状态数是 \(O(n)\) 的；\(g_{i,j}\) 的转移是 \(O(1)\) 的，状态数为 \(O(n\sqrt{n})\)，因此总时空复杂度是 \(O(n\sqrt{n})\) 的。

Reflect

遇到一段段转移状态，或者有很多段的操作/计数的长度和为 \(n\) 时，多想分块和根号分治，比较容易通过当 \({x} > \sqrt{n}\) 可以暴力转移，至多跳 \(\sqrt{n}\) 次；当 \({x} \le {\sqrt{n}}\) 时种类数 \(\le {\sqrt{n}}\)。

dp 转移状态时，差分、前缀和思想是很重要的点。

T3 P10801 [CEOI 2024] 海战*

T4 P11336 [NOISG 2020 Finals] Aesthetic*

10/31

考前一天，依旧体艺节，不过没怎么下去玩，几乎都在机房复习，晚上后面也逃出去看了 \(1h\) 晚会，放松身心嘛。

（音乐）淋一场雨，位于宿舍：

\(18:00\)，连续达成 \(23.87s\)（不跳步）和 \(21.90s\)（跳倒数第 \(2\) 步）

11/01

2025 CSP-S2 比赛日

早上按照计划复习了一下，看了一些文章什么的，还有部分模版，还算比较轻松。

中午浅睡 \(1h\)，精神恢复得不错，听说 J 组不难，会不会 S 组增大难度？？？

T1 一眼贪心，一开始想了一个简单的贪心（出来证明应该是对的），但是不敢下手，于是决定打反悔贪心，但是细节错误过不了大样例，已经 \(40min\) 了，说实话当时有点紧张，但是还是冷静下来，\(10min\) 在草稿纸模拟了一下大样例，在 \(1h\) 时改了出来。（打乱了我考前的安排，比预期慢了一倍）

期望得分：\(+100pts\)

T2 很明显的性质，先对没有乡镇的图做最小生成树，\(m\) 可以缩小成 \(n\) 的大小 \(\le {{10} ^ {4}}\)，由于 \({k} \le {10}\)，那么时间复杂度可能为 \(O(2^kn)\) 或者 \(O(2^kkn)\)，但是一直犹豫，总感觉不好实现（确实没想到怎么实现），怀疑有更加优秀的方法，耗了大概 \({40} \sim {50} min\)。

最后才觉得先打了暴力再说，然后就用 \(40min\) 左右打了 \(O(2^knk\log{nk})\) 的做法，才发现好像接近正解了，但是大样例跑得极其慢，分别是 \(1.7s,2.3s,1.6s\)。

接下来一直在想怎么优化，中间发现读入用了 \(1.5s\) 左右，想到可以加上快读，然后大样例都跑了 \(0.6s\) 左右，由于大样例没有极限数据，没什么时间构造大数据了，直接 \(\times {10}\) 跑了 \(0.8s\) 左右，希望 CCF 的少爷机跑得快一些吧。

这里其实差一点想到怎么优化：其他明细无法优化，只能优化 \(\log{nk}\)，那不妨提出去预处理，在每一次加入边的时候用桶维护，就能变成 \(O(2^knk)\) 了，考场上脑子短路了，太傻了qwq。用时 \(2h\)。

期望得分：\(+[80,100]pts\)

最后还剩 \(1h\)，感觉时间不太够用了，于是剩下的策略就是先打暴力保分。

先开的是 T4，暴力枚举可能的排列，并且判定即可；对于 \(n = m\) 的性质很容易想到是阶乘，\(20min\)。其中还想了一下性质 A，猜出来了 dp，可惜时间不够，没有时间继续想下去了。

期望得分：\(+12pts\)

然后开 T3，一眼想到哈希的 \(O(L^2)\) 做法，遂打，\(20min\) 过了样例，可惜没有这个范围的大样例，没法测试（打暴力的时候发现本题非常可做，但是没时间了）

出来发现没有特判 \(|t_1| \ne |t_2|\)，希望不要挂飞。

闲话：本题很经典，模拟赛做过类似的 trick 可以用根号做法（可能能过）；即使不用根号做法，本题的先找最长前后缀再在字典树上数点做法也很经典，可惜没什么时间想了，问题在于前面的时间分配不正确，耗时太长了。

期望得分：\(+[0,25]pts\)

期望总得分：\(100 + [80,100] + [0,25] + 12 = [192,237]pts\)，没达到考前的预期，对本次发挥感到不满意。

upd：\(100 + 80 + 25 + 12 = 217pts\)

有很多细节，非常值得反思：

题目：

T1 对一开始的简单贪心不够坚定；反悔贪心还没想好细节就开始写了，花了那么久去调确实不值得。
T2 对自己的想法也是犹犹豫豫，想优化时没有一眼确定正确的方向，而且没想到可以用桶预处理然后归并对 sort 做到优化（蠢）。
T3 主要没有时间了，而且还是老问题，看到字符串先想到的是哈希，并非字典树和 AC 自动机，考场上甚至没想过 KMP 之类，而且打暴力太急，没有多去思考更多分的暴力，像 \(50pts\) 的暴力其实也很好想。
T4 主要也是时间问题导致没时间去打性质了，考场上对性质其实已经有点想法了。

小总结问题：

时间分配：T1,T2 消耗的时间太不应该了，T1 由于打代码前没有想清楚，T2 最后的代码也是最初 \(20min\) 就已经想出来的思路。
心态：在 T1 耗了 \(1h\) 才改出来后明显在安排和心态上有一点波动，真的就得做出来后才做后面的题，这一次是运气好，跳到后面看 T2 时，想到模拟大样例，发现问题（平常打模拟赛的时候还是得多安排，规划，训练心态）。
知识点：若真的有时间，对于 T3，应该要想到字典树和 ACAM 的做法。还需要加强计数题，图论，字符串的能力（其实哪里都得加强，NOIP只会更难）。

闲话：考前复习到最小生成树的时候没想到会考，就背了一下模版；复习到 ACAM 时也没想到会考，太自以为是了，还想着前几年考过字符串了，即使考了也不会考 ACAM 做法吧。反倒是字典树还特别复习了一下，但是没用上。

回去加练。

NOIP 继续加油，调整好状态。

If you don't fall how are you going to know what getting up is like.

11/02 ∼ 11/04

\(22.79s\) （不跳步）

音乐：我走后，时间：11/04-17:00，地点：食堂二楼

\(21.43s\) （没记忆了，要么不跳步，要么跳倒数第 \(2\) 步）

时间：11/04-19:30，地点：科学楼 \(5\) 楼靠桥的走廊

11/05

嗜好

楼顶上的小斑鸠

赛勒斯的爱

苏公堤

提前出分？？？

\(100 + 80 + 25 + 12 = 217pts\)

没有惊喜也没有惊吓qwq希望下一次有惊喜。

11/06 ∼ 11/27

记录一些感觉需要的模拟赛题。

太摆烂了qwq

~~有时间一定补的好吧~~

11/25

\(11:00\) 时宿舍突然有人说看到了星星，然后出去数星星，有十来个，一闪闪的。

11/27

十几个人打完全场后，\(5:50\) 出现绝美晚霞，一开始整片天都是粉粉的，后面逐渐变成高级氛围感的蓝紫色相间，好美😍。

可惜没有相机，没法录视频啊啊啊！！！

特别是最外场有个投篮点，听着好几遍“塞勒斯的爱”投篮，可以看到那个篮网刚刚好能和后面的晚霞照应，加上面一点点树叶映衬，氛围拉满了，超级好看。就晚霞+刷网+粤语氛围感音乐，给我爽到了。

最后也是打到只剩一点紫色才走好吧。

遇到好景，运气佳佳，NOIP一定会赢的！！！

记得看大样例的输入输出，说不定有惊喜。

可以先考虑特殊性质或者一些特殊的结构、限制。

缩小范围，放松限制也可以哦。

积累小技巧：

multiset 可以当平衡树用。
证明贪心结论：反证法，交换论证法，打暴力验证法。

特别鸣谢

试题出于 GJOJ，来源众多。

有部分文献参考于洛谷上的题解。

有部分文献参考于 garbage_fish

posted @ 2025-09-09 16:38 Fireworks_Rise 阅读(61) 评论(1) 收藏举报

刷新页面返回顶部

Fireworks-Rise

GD OIer

2025年高一上学期停课备赛笔记

前言

09/01

T1

题面

Solution

Reflect

T2

题意

Solution

T3 P10681 [COTS 2024] 奇偶矩阵 Tablica

题意

Solution

T4 P11945 [KTSC 2025] 军事基地 / safezone

题意

Solution

09/04

T1 P13532 [OOI 2023] Buying gifts / 购买礼物

题意

Solution

Reflect

T2 P6583 回首过去

题意

Solution

Reflect

T3 P10207 [JOI 2024 Final] 马拉松比赛 2 / Marathon Race 2

题意

Solution

Reflect

T4 P10208 [JOI 2024 Final] 礼物交换 / Gift Exchange

题意

Solution

Reflect

09/06

T1 CF1497D Genius

题意

Solution

T2

题意

Solution

T3 P11340 [COI 2019] TENIS

题意

Solution

Reflect

T4 P12445 [COTS 2025] 数好图 / Promet

题意

Solution

09/11

T1

题意

Solution

Reflect

T2 CF1975D Paint the Tree

题意

Solution

T3 P12546 [UOI 2025] Convex Array

题意

Solution

T4 P11516 [CCO 2024] Summer Driving*

09/13

T1 P11662 [JOI 2025 Final] 方格染色 / Grid Coloring

题意

Solution

Reflect

T2 P12576 [UOI 2021] 数字图/AT_arc038_d [ARC038D] 有向グラフと数

题意

Solution

T3 P11986 [JOIST 2025] 救护车 / Ambulance*

T4 P11303 [NOISG 2021 Finals] Pond

题意

Solution

09/17

09/16 ∼ 09/19

09/20

09/22

T1 AT_abc302_g [ABC302G] Sort from 1 to 4

题意

Solution