应用拓扑讲义整理 Chapter 4. 范畴 / Chapter 5. 基本群（Fundamental Groups）

Chapter 4. 范畴论

4.1 范畴

Definition 4.1（范畴）范畴 \(\mathscr C\) 是一种代数结构，包括

• 一族对象 \(\text{obj}\mathscr C\)；

• 每对对象之间的映射集 \(\text{Hom}(A,B), \forall A,B\in \text{obj}\mathscr C\)；

• 映射集之间的二元运算 \(\times\)，满足

  \[\text{Hom}(A,B)\times \text{Hom}(B,C)\rightarrow \text{Hom}(A,C). \]

  写作 \((f,g)\mapsto g\circ f\)。称为映射的复合。

使得

• \(\text{Hom}(A,B)\) 是两两不交的；

• 结合律 \(h\circ (g\circ f) = (h\circ g)\circ f\)；

• 对任意 \(A\in \text{obj}\mathscr C\)，存在单位映射 \(\text{Id}_A\in \text{Hom}(A,A)\) 使得

  \[\forall B\in \text{obj}\mathscr C, \forall f\in \text{Hom}(B,A), \text{Id}_A\circ f = f; \\ \forall C\in \text{obj}\mathscr C, \forall g\in \text{Hom}(A,C), g\circ \text{Id}_A = g. \]

Example 4.2（集合范畴）令 \(\mathscr C = \mathbf{Sets}\)，\(\text{obj}\mathscr C\) 为全体集合，\(\text{Hom}(A,B)\) 为全体映射 \(A\rightarrow B\)，映射的复合就是通常的定义。

Example 4.3（拓扑空间范畴）令 \(\mathscr C = \textbf{Top}\)，\(\text{obj}\mathscr C\) 为全体拓扑空间，\(\text{Hom}(A,B)\) 为全体连续函数 \(A\rightarrow B\)，映射的复合就是通常的定义。

Exercise 4.4 证明在一个确定的域 \(\mathbb F\) 上的全体线性空间形成了一个范畴。\(\mathbb F\) 自身是否是这个范畴里的对象？

Proof：令 \(\text{obj}\mathscr C\) 为 \(\mathbb F\) 上的全体线性空间，\(\text{Hom}(A,B)\) 为 \(A\) 到 \(B\) 的全体线性映射，映射的复合就是通常的定义。

因为 \(\mathbb F\) 可以作为其自身上的线性空间，所以 \(\mathbb F\in \text{obj}\mathscr C\)。

Exercise 4.5 证明全体图和图映射形成了一个范畴。

Proof：令 \(\text{obj}\mathscr C\) 为全体图，\(\text{Hom}(A,B)\) 为 \(A\) 到 \(B\) 的全体图映射，即满足

\[\begin{aligned} f = \{f_N: N_G\rightarrow N_J, f_E: E_G\rightarrow E_J\cup N_J\}, \\ f_E(AB) = \begin{cases} f_N(A)f_N(B), & f_N(A)\neq f_N(B); \\ f_N(A), & f_N(A) = f_N(B). \end{cases} \end{aligned} \]

并令 \(g\circ f = (g_N\circ f_N, g_E\circ f_E)\)。

Exercise 4.6 证明恒等映射是唯一的。

Proof：假设 \(\text{Id}_A\) 和 \(\text{Id}'_A\) 都是 \(A\) 上的恒等映射，即 \(\text{Id}_A\circ f = f, g\circ \text{Id}'_A = g\)。此时令 \(f = \text{Id}'_A, g = \text{Id}_A\) 则 \(\text{Id}_A = \text{Id}'_A\)。

Definition 4.7（子范畴）称范畴 \(\mathscr C\) 是范畴 \(\mathscr A\) 的子范畴如果

• \(\text{obj}\mathscr C\subset \text{obj}\mathscr A\)；
• \(\forall A,B\in \text{obj}\mathscr C, \text{Hom}_{\mathscr C}(A,B)\subset \text{Hom}_{\mathscr A}(A,B)\)；
• \(\mathscr C\) 上的复合运算是 \(\mathscr A\) 上复合运算的限制。

Example 4.8 范畴 \(\mathbf{Top}\) 的子范畴例如

• 将 \(\text{obj}\mathscr C\) 限制为 Hausdorff 空间、紧空间、欧氏空间等；
• 将映射限制为可微映射、解析映射等。

Example 4.9（群范畴）令 \(\mathscr C = \mathbf{Groups}\)，\(\text{obj}\mathscr C\) 为全体群，\(\text{Hom}(A,B)\) 为 \(A\) 到 \(B\) 的全体群同态，复合运算为通常定义。

Example 4.10（阿贝尔群范畴）令 \(\mathscr C = \mathbf{Ab}\)，\(\text{obj}\mathscr C\) 为全体阿贝尔群，\(\text{Hom}(A,B)\) 为 \(A\) 到 \(B\) 的全体群同态，复合运算为通常定义。

Definition 4.11（交换图）范畴 \(\mathscr C\) 上的图中的顶点为范畴的对象，边为范畴的映射；图的路径是一列映射的复合；\(\mathscr C\) 上的交换图是任意两条路径作为映射都相等的图。

Definition 4.12（共轭）范畴 \(\mathscr C\) 上的共轭是类 \(\cup_{(A,B)}\text{Hom}(A,B)\) 上的等价关系，满足

• \(f\in \text{Hom}(A,B),f\sim f' \quad \Rightarrow \quad f'\in \text{Hom}(A,B)\)；

• \(f\sim f'. g\sim g' \quad \Rightarrow g\circ f\sim g'\circ f'\)。

Lemma 4.13 设 \(\mathscr C\) 上定义了共轭关系 \(\sim\)，\([f]\) 为共轭关系下映射 \(f\) 所在的等价类。定义 \(\mathscr C'\) 为

\[\begin{cases} \text{obj}\mathscr C := \text{obj}\mathscr C' \\ \text{Hom}_{\mathscr C'}(A,B) := \{[f]: f\in \text{Hom}_\mathscr C(A,B)\} \\ [g]\circ [f] := [g\circ f]. \end{cases} \]

则 \(\mathscr C'\) 是一个范畴。

Definition 4.14（商范畴）Lemma 4.13 定义的范畴 \(\mathscr C'\) 称为 \(\mathscr C\) 的商范畴。一般也称 \(\text{Hom}_{\mathscr C'}(A,B)\) 为 \([A,B]\)。

Example 4.15 令 \(\mathscr C = \mathbf{Groups}\)，\(f,g\in \text{Hom}(G,H)\)。定义 \(f\sim g\) 如果

\[\exists a\in H, \quad \text{s.t.} \quad \forall x\in G, f(x) = ag(x)a^{-1}, \]

下面证明 \(\sim\) 是共轭关系。

假设 \(f\sim f', g\sim g'\)，且 \(g\circ f\) 存在，则

\[\begin{aligned} g(f(x)) &= g(af'(x)a^{-1}) = bg'(af'(x)a^{-1})b^{-1} \\ &= bg'(a)g'(f'(x))g'(a^{-1})b^{-1} \\ &= bg'(a)g'(f'(x))(bg'(a))^{-1}, \end{aligned} \]

因此 \(g\circ f\sim g'\circ f'\)。

4.2 函子

Definition 4.16（协变函子）设 \(\mathscr A\) 和 \(\mathscr C\) 是两个范畴，则协变函子 \(T: \mathscr {A\to C}\) 是范畴间的映射，满足

• \(A\in \text{obj}\mathscr A \Rightarrow TA\in \text{obj}\mathscr C\)；
• 若 \(f: A\to A'\) 是 \(\mathscr A\) 上的映射，则 \(Tf: TA\rightarrow TA'\) 是 \(\mathscr C\) 上的映射。
• 若 \(f,g\) 是 \(\mathscr A\) 上的映射且 \(g\circ f\) 有定义，则 \(T(g\circ f) = (Tg)\circ (Tf)\)。即如下交换图成立：

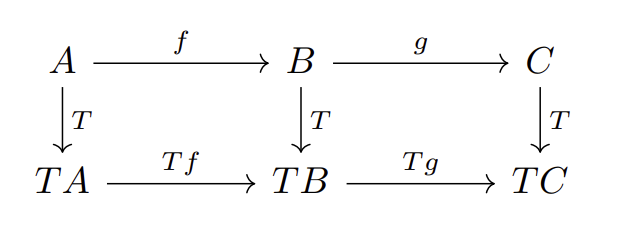
• \(\forall A\in \text{obj}\mathscr A\)，\(T(\text{Id}_A) = \text{Id}_{TA}\)。

Definition 4.17（单位函子）对于范畴 \(\mathscr C\)，单位函子 \(J: \mathscr {C\to C}\) 定义为 \(JA = A, Jf = f\)。

Example 4.18 设 \(\mathscr A\) 是全体有限图构成的范畴。则图的 \(0\)-链群和 \(1\)-链群都可以通过协变函子 \(T: \mathscr A\to \mathbf{Ab}\) 构造。图映射 \(\{f\}\subset \text{Hom}\mathscr C\) 对应链映射 \(\{Tf\}\subset \mathbf{Ab}\)。

Example 4.19 将上例的图换成立方复形，则有立方复形到 \(\mathbf{Ab}\) 的协变函子。

Example 4.20 忘却函子 \(F: \mathbf{Top}\to\mathbf{Sets}\) 将拓扑空间映射到其本身，将连续映射也映射到本身，但忽略其拓扑性质。\(\mathbf{Groups}\to \mathbf{Sets}\) 和 \(\mathbf{Ab}\to\mathbf{Groups}\) 也是类似。

Definition 4.21（诱导协变函子）设 \(A,B\in \text{obj}\mathscr C\)，则在 \(\text{Hom}(A,B)\in \text{Hom}\mathscr C\) 上定义的诱导协变函子 \(\text{Hom}(A,):\mathscr C\to\mathbf{Sets}\) 定义为

\[\text{Hom}(A,f): \text{Hom}(A,B)\rightarrow \text{Hom}(A,B'), g\mapsto f\circ g \]

称为诱导协变函子。通常也记 \(\text{Hom}(A,f) = f_*\)。

Example 4.22 设 \(A\) 为线性空间。则对线性映射 \(f: B\to C\)，在线性空间 \(B\) 上定义的诱导线性映射 \(\text{Hom}(A,)\) 是 \(f_*: \mathcal L(A,B)\to \mathcal L(A,C), f_*(g) = f\circ g\)。

Definition 4.23（反变函子）设 \(\mathscr A\) 和 \(\mathscr C\) 是两个范畴，则反变函子 \(S: \mathscr {A\to C}\) 是范畴间的映射，满足

• \(A\in \text{obj}\mathscr A \quad \Rightarrow \quad SA\in \text{obj}\mathscr C\)；
• 若 \(f: A\to A'\) 是 \(\mathscr A\) 中映射，则 \(Sf: SA'\to SA\) 是 \(\mathscr C\) 中映射。即满足交换图

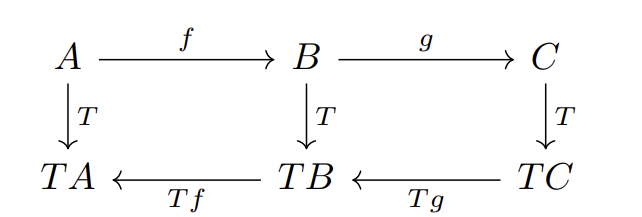
• 若 \(f,g\) 是 \(\mathscr A\) 中映射，\(g\circ f\) 有定义，则 \(S(g\circ f) = (Sf)\circ (Sg)\)。
• 对任意 \(A\in \text{obj}\mathscr A\)，\(S(\text{Id}_A) = \text{Id}_{SA}\)。

Example 4.24 设 \(\mathscr A\) 是全体有限图构成的范畴。则图的 \(0\)-反链群和 \(1\)-反链群都可以通过反变函子 \(T: \mathscr A\to \mathbf{Ab}\) 构造。图映射 \(\{f\}\subset \text{Hom}\mathscr A\) 对应反链映射 \(\{Tf\}\subset \mathbf{Ab}\)。

Example 4.25 将上例的图改为立方复形，则有立方复形到 \(\mathbf{Ab}\) 的反变算子。

Definition 4.26（诱导反变函子）设 \(B\in \text{obj}\mathscr C\)，则在 $ \text{Hom}(A,B)\in \text{Hom}\mathscr C$ 上定义的诱导反变函子 \(\text{Hom}(,B): \mathscr C\to \mathbf{Sets}\) 定义为

\[\text{Hom}(g,B): \text{Hom}(A',B)\to \text{Hom}(A,B), h\mapsto h\circ g \]

称为诱导反变函子。通常也记 \(\text{Hom}(g,B) = g^*\)。

Example 4.27 设 \(\mathscr C_{\mathbb F}\) 为 \(\mathbb F\) 上的全体线性空间。则对偶空间函子是反变函子 \(S: \mathscr C_{\mathbb F}\to \mathscr C_{\mathbb F}\)，\(S(V) = V', S(T) = T'\)，其中 \(V' = \mathcal L(V,\mathbb F)\) 为 \(V\) 的对偶空间，\(T': W'\rightarrow V'\) 定义为 \(T'(\varphi) = \varphi\circ T\) 是 \(T: V\to W\) 的对偶映射。

Exercise 4.28 设 \(\mathscr C\) 和 \(\mathscr A\) 是范畴，\(\sim\) 是 \(\mathscr C\) 上的共轭关系，\(\mathscr C'\) 是对应商群。证明：若函子 \(T: \mathscr C\to \mathscr A\) 满足 \(T(f) = T(g), \forall f\sim g\)，则 \(T\) 诱导了函子 \(T': \mathscr C' \to \mathscr A\)，

\[\begin{aligned} \forall X\in \mathscr C ,& T'(X) = T(X), \\ \forall f\in \text{Hom}(A,B) ,& T'([f]) = T(f). \\ \end{aligned} \]

Proof：定义 \(T'([f]) = T(f)\)。因为 \(T(f)=T(g),\forall f\sim g\)，所以 \(T'\) 是两定义的。我们只需验证 \(T'\) 是函子。因为

\[T'([g]\circ [f]) = T'([g\circ f]) = T(g\circ f) = (Tg)\circ (Tf) = T'([g])\circ T'([f]). \]

Definition 4.29（等价映射）称范畴 \(\mathscr C\) 中的两个映射 \(f: A\to B\) 是等价映射，如果存在 \(g: B\to A\) 使得 \(f\circ g = \text{Id}_B, g\circ f = \text{Id}_A\)。

Exercise 4.30 验证以下映射是等价。（1）\(\mathbf{Sets}\) 中的双射；（2）\(\mathbf{Top}\) 中的同胚；（3）\(\mathbf{Groups}\) 中的同构；（4）\(\mathbf{Top}\) 中所有满足 \(f: (X,A)\to (X',A')\)，\(f: X\to X'\) 为满足 \(f(A) = A'\) 的同胚。

Proof：

（1）对任意集合 \(A\) 和 \(B\) 之间的双射 \(f: A\to B\)，定义 \(g(f(x)) = x, \forall x\in A\)，则 \(f\circ g = \text{Id}_A, g\circ f = \text{Id}_B\)。\(g\) 也是 \(f\) 的逆映射。

（2）对任意拓扑空间 \(X\) 和 \(Y\) 之间的同胚 \(f: X\to Y\)，根据同胚映射的定义，其逆映射 \(f^{-1}: Y\to X\) 也是连续映射。

（3）对任意群 \(G\) 和 \(H\) 之间的同构 \(f: G\to H\)，根据同构映射的定义，其逆映射 \(f^{-1}: H\to G\) 也是同胚映射。

（4）？

Exercise 4.31 证明群 \((G,*)\) 是范畴。

Proof：令全体集合的 class 为 \(\text{obj}\mathscr G\)，群元素在集合 \(A\) 到 \(B\) 的作用为 \(\text{Hom}(A,B)\)。

Theorem 4.32 设 \(\mathscr A\) 和 \(\mathscr C\) 是两个范畴。若 \(T: \mathscr A\to \mathscr C\) 是协变或反变算子，\(f\) 是 \(\mathscr A\) 的等价映射，则 \(Tf\) 是 \(\mathscr C\) 的等价映射。

Chapter 5. 基本群

5.1 同伦

5.1.1 同伦范畴

Definition 5.1（同伦）称两个连续映射 \(f,f': X\to Y\) 同伦，如果存在连续映射 \(F\times [0,1]\to Y\) 使得

\[\forall x\in X, F(x,0) = f(x); F(x,1) = f'(x). \]

映射 \(F\) 称为 \(f\) 到 \(f'\) 的同伦映射。

Example 5.2 圆柱 \(f: I^2\to \mathbb R^3\) 到圆周 \(g: I^2\to \mathbb R^3\) 的连续形变是同伦

\[\begin{aligned} F(\theta, z, t) &= tg(\theta, z) + (1-t)f(\theta, z); \\ f(\theta, z) &= (\cos 2\pi\theta, \sin 2\pi\theta, z), \\ g(\theta, z) &= (\cos 2\pi\theta, \sin 2\pi\theta, 0). \\ \end{aligned} \]

Definition 5.3（直线同伦）两个同伦映射 \(f,g\) 的直线同伦为

\[F(x,t) = (1-t)f(x) + tg(x). \]

Lemma 5.4 设 \(U\) 是 \(\mathbb R^n\) 中凸集，\(n\in \mathbb N\)。则任意映射 \(f,g: X\to U\) 同伦。

Proof：直线同伦即为同伦映射。

Exercise 5.5 将英文字母分组为同伦等价类。

Proof：

• C，E，F，G，H，I，J，K，L，M，N，S，T，U，V，W，X，Y，Z
• A，D，O，P，Q，R
• B

Lemma 5.6 假设 \(h,h': X\to Y\) 同伦，\(k,k': Y\to Z\) 同伦，则 \(k\circ h \cong k'\circ h'\)。

Proof：设 \(H(x,t)\) 和 \(K(y,t)\) 是分别是 \(h,h'\)、\(k,k'\) 的同伦映射，则 \(F(x,t) = K(H(x,t),t)\) 是 \(k\circ h\) 与 \(k'\circ h'\) 的同伦映射。

Theorem 5.7 同伦是 \(X\to Y\) 的全体连续映射 \(\mathcal C(X,Y)\) 上的等价类。

Proof：只需证明传递性。设 \(F\) 是 \(f\) 到 \(f'\) 的同伦映射，\(F'\) 是 \(f'\) 到 \(f''\) 的同伦映射。则函数

\[G(x,t) = \begin{cases} F(x,2t), & t\in [0,\frac 12]; \\ F'(x,2t-1), & t\in [\frac 12, 1] \end{cases} \]

是良定义的，因为 \(t = \frac 12\) 时 \(F(x,2t) = f' = F'(x,2t-1)\)。

由黏结引理，\(G\) 是连续映射，故也是 \(f\) 到 \(f''\) 的同伦映射。

Definition 5.8（连续映射的同伦等价类）\(f: X\to Y\) 的等价类是

\[[f] := \{g\in \mathcal C(X,Y): g\cong f\}. \]

连续映射的同伦等价类 \(X\to Y\) 为

\[[X,Y] := \mathcal C(X,Y)/\cong. \]

Example 5.9 任意连续映射 \(f: X\to \mathbb R\) 和 \(g: X\to \mathbb R\) 都通过直线同伦映射同伦。因此 \([X,\mathbb R]\) 是单元素集合。特别地，\([\mathbb {R,R}] = \{[0]\}\)，即任意实函数都同伦。

Lemma 5.10 \([h]=[h'],[k]=[k']\Rightarrow [h\circ k]=[h'\circ k']\)。

Corollary 5.11 同伦是范畴 \(\mathbf{Top}\) 上的共轭。

Definition 5.12（同伦范畴）同伦范畴 \(\mathbf{hTop}\) 是范畴 \(\mathbf{Top}\) 在同伦共轭下的商范畴。

Exercise 5.13 证明：\(\text{obj}(\mathbf{hTop}) = \text{obj}(\mathbf{Top}), \text{Hom}(X,Y) = [X,Y], [g]\circ [f] = [g\circ f]\)。特别地，\([X,X]\) 的单位元是 \([\text{Id}_X]\)。

Proof：由 Definition 4.14 知

\[\begin{cases} \text{obj}(\mathbf{hTop}) = \text{obj}(\mathbf{Top}); \\ \text{Hom}(X,Y) = \{[f]: f\in \text{Hom}_{\mathbf{Top}}(X,Y)\} = [X,Y]; \\ [g] \circ [f] = [g\circ f]. \end{cases} \]

Definition 5.14（同伦等价）称连续映射 \(f: X\to Y\) 是同伦等价如果存在另一个连续映射 \(g: Y\to X\) 使得 \(f\circ g \cong \text{Id}_Y, g\circ f \cong \text{Id}_X\)。称两个拓扑空间 \(X\) 和 \(Y\) 同伦等价如果存在同伦等价 \(f: X\to Y\)。

Example 5.15 经典的杯子和甜甜圈同伦

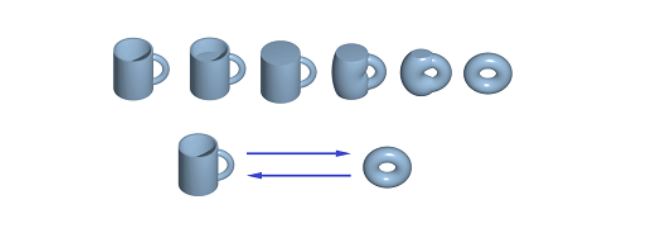
Example 5.16 Example 5.2 可从另一个角度解释：圆柱 \(X = \mathbb S^1\times I\) 和环 \(Y = \mathbb S^1\times \{0\}\) 通过投影映射 \(p(x,y,z) = (x,y)\) 和嵌入映射 \(e(x,y) = (x,y,0)\) 等价。

Exercise 5.17 证明 \(f: X\to Y\) 是同伦等价当且仅当 \([f]\in [X,Y]\) 是 \(\mathbf{hTop}\) 上的等价。

Proof：\(f: X\to Y\) 是同伦等价，

\(\Leftrightarrow\) 存在 \(g: Y\to X\)，\(f\circ g \cong \text{Id}_Y, g\circ f \cong \text{Id}_X\)，

\(\Leftrightarrow\) 存在 \(g: Y\to X\)，\([f\circ g] = [\text{Id}_Y], [g\circ f] = [\text{Id}_X]\)，

\(\Leftrightarrow\) 存在 \([g]\in [Y,X]\)，\([f]\circ [g] = [\text{Id}_Y], [g]\circ [f] = [\text{Id}_X]\)，

\(\Leftrightarrow\) \([f]\) 是 \(\mathbf{hTop}\) 上的等价。

5.1.2 零伦映射

Definition 5.18（零伦）称 \(f: X\to Y\) 是零伦的如果存在常值映射 \(f': X\to Y\) 使得 \(f\cong f'\)。

Theorem 5.19 对任意连续映射 \(f: \mathbb{S}^n\to Y\)，以下等价：

• \(f\) 零伦；

• \(f\) 可被延拓为连续映射 \(g: \mathbb{D}^{n+1}\to Y\)；

• 对连续映射 \(k: \mathbb{S}^n\to Y\)，\(k(x) = f(x_0)\)，\(x_0\in \mathbb S^n\)，有

  \[\exists F: f\cong k, \text{s.t.}\forall t\in I, F(x_0,t) = f(x_0). \]

Proof：\((1)\Rightarrow (2)\)：给定 \(F: f\cong c, c(x) = y_0, \forall x\in \mathbb S^n\)，构造 \(g: \mathbb D^{n+1}\to Y\) 使得

\[g(x) = \begin{cases} y_0, & \Vert x\Vert\in [0,\frac 12]; \\ F(\frac x{\Vert x\Vert}, 2-2\Vert x\Vert), & \Vert x\Vert \in [\frac 12, 1]. \end{cases} \]

则容易验证 \(g\) 连续且 \(g(x) = f(x), \forall x\in \mathbb S^n\)。

\((2)\Rightarrow (3)\)：定义 \(F: \mathbb S^n\times I\to Y\)，

\[F(x,t) = g((1-t)x + tx_0). \]

则因为 \(x_0\) 是固定的，所以

\[\{(1-t)x+tx_0:x\in \mathbb S^n\} = \mathbb D^{n+1}. \]

显然 \(F\) 连续且 \(F(x_0,t) = g(x_0),\forall t\)。

\((3)\Rightarrow (1)\)：trivial。

5.1.3 可缩空间

Definition 5.20（可缩空间）称空间 \(X\) 是可缩的，如果单位映射 \(\text{Id}_X: X\to X\) 零伦。

Example 5.21 \([0,1]\) 和 \(\mathbb R\) 可缩，因为连续映射 \(F(t,x) = tx\) 是 \(\text{Id}\) 到 \(0\) 的同伦。

Theorem 5.22 \(X\) 中任意凸集都是可缩的。

Proof：选定任意 \(x_0\in X\)，定义 \(c: X\to X, c(x) = x_0\)。则直线同伦即满足要求。

Exercise 5.23 证明可缩空间是道路连通的。

Proof：对任意的 \(x\in X\)，因为存在同伦 \(F\) 使得 \(F(0,x) = x, F(1,x) = x_0\)，所以 \(x\) 与 \(x_0\) 通过曲线 \(F(\cdot, x)\) 连通。由 \(x\) 的任意性，\(X\) 中任意两个点均道路连通。

Example 5.24 Exercise 5.23 的逆命题是错误的：道路连通空间 \(\mathbb S^1\) 是不可缩的。

Definition 5.25（映射锥）空间 \(X\) 的映射锥，记为 \(CX\)，为商空间 \(X\times I / \sim\)，其中等价关系是 \((x,1)\sim (x',1)\)。等价类 \((x,t)\) 记作 \([x,t]\)，特别地，\([x,1]\) 称为 \(CX\) 的顶点。

Exercise 5.26 证明连续映射 \(f: X\times I\to Y\) 诱导了另一个连续映射 \(\overline f: CX\to Y\)，\(\overline f([x,t]) = f(x,t)\)。

Proof：由 Theorem 1.230，连续映射 \(f\) 诱导了唯一的映射 \(\overline f\) 使得 \(f = \overline f\circ p\)。其中 \(p\) 是 \(X\times I / \sim\) 对应的商映射。

Lemma 5.27 设 \(X,Y\) 是拓扑空间，\(f: X\times I\to Y\) 满足 \(f(x,1) = y_0, \forall x\in X\)。则 \(f\) 诱导了映射 \(\overline f: CX\to Y\)，\(\overline f([x,t]) = f(x,t)\)。进一步地，\(\overline f\) 连续当且仅当 \(f\) 连续。

Lemma 5.28 \(\mathbb S^n\) 的映射锥同胚于 \(\mathbb D^{n+1}\)，即

\[C\mathbb S^n \cong \mathbb D^{n+1}. \]

Exercise 5.29 证明 Lemma 5.28。

Proof：\(f((x_1,x_2,\dots,x_n),t) = (tx_1,tx_2,\dots,tx_n,\sqrt {1-t^2})\) 是 \(C\mathbb S^n\) 到 \(\mathbb D^{n+1}\) 的同胚映射。

Theorem 5.30 任意空间 \(X\) 上的映射锥 \(CX\) 都是可缩空间。

Proof：定义零同胚 \(F: CX\times I\to CX\) 为

\[F([x,t],s) = [x,(1-s)t+s]. \]

显然 \(F([x,t],0) = \text{Id}_{CX}\)，\(F([x,t],1) = [x,1]\)。

Theorem 5.31 空间 \(X\) 与单点同伦当且仅当 \(X\) 可缩。

Proof：设 \(\{a\}\) 是单点空间，假设 \(X\) 和 \(\{a\}\) 同伦。则由 Definition 5.14，存在连续映射 \(f: X\to \{a\}\) 和 \(g: \{a\}\to X\) 使得 \(g\circ f \cong \text{Id}_X\)，\(f\circ g = \text{Id}_{\{a\}}\)。而 \(g\circ f = g(a)\) 是常值映射，所以 \(\text{Id}_X\) 零伦，\(X\) 可缩。

假设 \(\text{Id}_X\cong k\)，其中 \(k(x) = x_0\in X\)。则只能有 \(f: X\to \{x_0\}, f(x) = x_0\)。定义 \(g: \{x_0\}\to X\) 为 \(g(x_0) = x_0\)，则由 Definition 5.14，\(f\) 是同伦。

Theorem 5.32 若 \(Y\) 可缩，则任意两个 \(X\to Y\) 的映射同伦，且都是零伦的。

Proof：假设 \(Y\) 可缩，则有恒等映射和常值映射之间的同伦 \(F(y,t)\)。\(\text{Id}_Y(y) = y = F(y,0)\)，\(g(y) = z = F(y,1)\)。由 Lemma 5.6，任意连续映射 \(f: X\to Y\) 都与 \(h(x) = (g\circ f)(x) = z\) 同伦。

Exercise 5.33 证明 \([X,Y]\) 是单元素集合如果 \(X\) 可缩且 \(Y\) 道路连通。

Proof：设 \(X\) 可缩，则对任意 \(f\in \mathcal C(X,Y)\)，\(f\) 与常值映射同胚。因为 \(Y\) 道路连通，所以任意常值映射均同胚。所以 \([X,Y]\) 是单元素集合。

5.2 道路同伦

Definition 5.34（道路同伦）两个道路 \(f,f'\) 道路同伦，记作 \(f\cong_p f'\)，如果它们的起点 \(x_0\) 和终点 \(x_1\) 相同，且存在连续映射 \(F: I\times I\to X\) 使得

\[\begin{aligned} \forall s\in I, & F(s,0) = f(s), F(s,1) = f'(s); \\ \forall t\in I, & F(0,t) = x_0, F(1,t) = x_1. \\ \end{aligned} \]

称 \(F\) 是道路同伦。

Example 5.35 设 \(X = \mathbb R^2\backslash \{0\}\)。对以下道路

\[\begin{aligned} f(s) & = (\cos\pi s, \sin \pi s), \\ g(s) & = (\cos \pi s, 2\sin \pi s), \\ h(s) & = (\cos \pi s, -\sin \pi s), \\ \end{aligned} \]

则 \(f\cong_p g\)（直线同伦），而 \(g\) 与 \(h\) 不同伦。

Definition 5.36（道路乘积）对两条道路 \(f,g : [0,1]\to X\)，\(f(1) = g(0)\)，它们的道路乘积 \(f*g\) 是

\[(f*g)(s) = \begin{cases} f(2s), & s\in [0,\frac 12]; \\ g(2s-1), & s\in [\frac 12, 1]. \\ \end{cases} \]

Lemma 5.37 对两条道路 \(f,g: [0,1]\to X\) 满足 \(f(1) = g(0)\) 和连续映射 \(k: X\to Y\)，有

\[k\circ (f*g) = (k\circ f)*(k\circ g). \]

Lemma 5.38 对连续映射 \(k: X\to Y\) 和 \(f\) 与 \(f'\) 之间的道路同胚 \(F\)，\(k\circ F\) 是 \(Y\) 中 \(k\circ f\) 与 \(k\circ f'\) 之间的道路同胚。

Definition 5.39（道路同胚等价类的乘积）对两个道路 \(f,g: [0,1]\to X\)，\(f(1) = g(0)\)，它们的等价类 \([f]\) 与 \([g]\) 的乘积是

\[[f]*[g] := [f*g] \]

Exercise 5.40 验证 Definition 5.39 是良定义。

Proof：只需验证：若 \(f\cong f', g\cong g'\)，则 \(f*g\cong f'*g'\)。

设 \(f\) 和 \(f'\) 通过 \(F\) 同胚，即 \(f = F(0,\cdot), f' = F(1,\cdot)\)；\(g\) 和 \(g'\) 通过 \(G\) 同胚，即 \(g = G(0,\cdot),, g' = G(1,\cdot)\)。定义

\[H(s,t) = \begin{cases} F(2s,t), & s\in [0,\frac 12]; \\ G(2s-1,t), & s\in [\frac 12, 1]. \\ \end{cases} \]

则 \(H\) 是 \(f*g\) 和 \(f'*g'\) 之间的同胚。

Defenition 5.41（局部函数）设 \(X'\subset X\)，称 \(f': X'\to Y\) 为 \(X\) 到 \(Y\) 的局部函数。

Definition 5.42（广群）广群是一个三元组 \((G, \cdot, ^{-1})\)，其中 \(G\) 是一个集合，\(\cdot: G\times G\to G\) 是局部函数，\(^{-1}: G\to G\) 是一元算子。满足

• 结合性：若 \(a\cdot (b\cdot c)\) 有定义，则 \((a\cdot b)\cdot c = a\cdot (b\cdot c)\)；
• 逆元性：对任意 \(a\in G\)，存在 \(a^{-1}\in G\) 使得 \(a\cdot a^{-1}\) 和 \(a^{-1}\cdot a\) 都有定义；
• 单位性：若 \(a\cdot b\) 有定义，则 \(a\cdot b\cdot b^{-1} = a\) 且 \(a^{-1}\cdot a\cdot b = b\)。

Theorem 5.43 道路同伦等价类形成了一个广群 \((P, *, ^-)\)，其中 "\(*\)" 是道路乘积，\(^-\) 是道路反转，

\[f^-(s) := f(1-s). \]

特别地，若 \(f\) 是从 \(x_0\) 到 \(x_1\) 的道路，\(e_x: I\to X\) 是常值映射，\(e_x(t) = x, \forall t\in I\)，则有

• 若 \(\alpha = ([f]*[g])*[h]\) 有定义，则 \(\beta = [f] * ([g] * [h])\) 也有定义且 \(\alpha = \beta\)；
• \([f] * [f^-] = e_{x_0}\) 且 \([f^-] * [f] = e_{x_1}\)；
• \([f] * [e_{x_1}] = [f] = [e_{x_0}] * [f]\)。

Proof：首先证明假设 \([g] * [f]\) 有定义，则 \([g] * [f] * [f^-] = [g] * [e_{x_1}] = [g]\)。

定义 \(i_I^-(s) := i_I(1-s) = 1-s\)。则

\[\begin{aligned} & i_I \cong e_0 * i_I \Rightarrow f\circ i_I \cong (f\circ e_0) * (f\circ i_I) \\ \Rightarrow & f \cong e_{x_0} * f\Rightarrow [f] = [e_{x_0} * f] = [e_{x_0}] * [f], \end{aligned} \]

类似地，有

\[\begin{aligned} & i_I * i_I^- \cong e_0 \Rightarrow (f\circ i_I) * (f\circ i_I^-) \cong (f\circ e_0) \\ \Rightarrow & f * f^- \cong e_{x_0} \Rightarrow [f] * [f^-] = [e_{x_0}]. \end{aligned} \]

因此 \(P\) 具有单位性。

再假设 \(f(1) = g(0), g(1) = h(0)\)，则 \(f*g*h\) 有定义。即 \(P\) 具有结合性。

Definition 5.44（正线性映射）闭区间 \([a,b]\) 到 \([c,d]\) 的正线性映射定义为线性双射 \(p(x) = mx+k\)。

Theorem 5.45 设 \(f\) 是 \(X\) 中的道路，\(0 = a_0 < a_1 < \dots < a_n = 1\)。定义 \(I_j := [a_{j-1}, a_j]\) 和 \(f_j = f\circ p_j\)，\(p_j: I\to I_j\) 是正线性映射。则有

\[[f] = [f_1] * [f_2] * \dots * [f_n]. \]

Proof：

\[i_I \cong p_1 * p_2 * \dots * p_n \Rightarrow f\circ i_I \cong f\circ (p_1*p_2*\cdots * p_n) = f_1 * f_2 * \dots * f_n. \]

所以 \([f] \cong [f\circ i_I] \cong [f_1]*[f_2]\dots * [f_n]\)。

5.3 基本群

Definition 5.46（以 \(x_0\) 为基的环）以 \(x_0\) 为基的环是 \(X\) 中起点和终点均为 \(x_0\) 的路径。

Definition 5.47（基本群 / 一阶同伦群）拓扑空间 \(X\) 中以 \(x_0\) 为基的基本群，记作 \(\pi_1(X, x_0)\)，定义为全体基于 \(x_0\) 的环形成的同伦等价类。

Example 5.48 若 \(X\) 为 \(\mathbb R\) 中凸集，则 \(\pi_1(X, x_0)\) 是单元素集合。

Definition 5.49 对从 \(x_0\) 到 \(x_1\) 的道路 \(\alpha : I\to X\)，定义映射 \(\hat\alpha : \pi_1(X, x_0)\to \pi_1(X, x_1)\) 为

\[\hat\alpha([f]) := [\alpha^-] * [f] * [\alpha]. \]

Theorem 5.50 映射 \(\hat\alpha\) 是群同构。

Proof：

\[\hat\alpha([f]) * \hat\alpha([g]) = [\alpha^-] * [f] * [\alpha] * [\alpha^-] * [g] * [\alpha] = [\alpha^-] * [f * g] * [\alpha] = \hat\alpha([f*g]). \]

定义 \(\beta = \alpha^-\)，则易证 \(\hat\beta\) 是 \(\hat\alpha\) 的左逆和右逆。

Exercise 5.51 设 \(\alpha\) 是 \(X\) 中从 \(x_0\) 到 \(x_1\) 的道路，\(\beta\) 是 \(X\) 中从 \(x_1\) 到 \(x_2\) 的道路。证明若 \(\gamma = \alpha * \beta\)，则 \(\hat\gamma = \hat\beta\circ\hat\alpha\)。

Proof：

\[\begin{aligned} \hat\gamma([f]) &= [\gamma^-] * [f] * [\gamma] \\ &= [(\alpha * \beta)^-] * [f] * [\alpha * \beta] \\ &= [\beta^-] * [\alpha^-] * [f] * [\alpha] * [\beta] \\ &= [\beta^-] * \hat\alpha([f]) * [\beta] \\ &= \hat\beta (\hat\alpha([f])). \end{aligned} \]

Corollary 5.52 对连通空间 \(X\)，\(x_0, x_1\in X\)，则 \(\pi_1(X, x_0) \cong \pi_1(X, x_1)\)。

Exercise 5.53 设 \(x_0\) 和 \(x_1\) 是道路连通空间 \(X\) 中的两个点。证明 \(\pi_1(X,x_0)\) 是阿贝尔群当且仅当对任意两条从 \(x_0\) 到 \(x_1\) 的道路 \(\alpha\) 和 \(\beta\)，有 \(\hat\alpha = \hat\beta\)。

Proof：（1）必要性：即证明对任意两条道路 \(f,g\) 都有 \([f]*[g] = [g]*[f]\)。设 \(x_1 = f(\frac 12)\)，\(\alpha = f([0, \frac 12]), \beta = f([1, \frac 12])\)，则 \(f = \alpha \circ \beta^-\)。

因为 \(\alpha\) 和 \(\beta\) 都是 \(x_0\) 到 \(x_1\) 的道路，所以 \(\hat{\alpha} = \hat{\beta}\)，所以

\[[\alpha^-]*[g]*[\alpha] = [\beta^-]*[g]*[\beta]. \]

两边同时左乘 \([\alpha]\) 并右乘 \([\beta^-]\) 得

\[[g]*[\alpha]*[\beta^-] = [\alpha]*[\beta^-]*[g], \]

即 \([g]*[f] = [f]*[g]\)。

（2）充分性：设 \(\alpha\) 和 \(\beta\) 都是从 \(x_0\) 到 \(x_1\) 的道路，\(f = \alpha\circ \beta^-\)，则对任意基于 \(x_0\) 的环路 \(g\) 有

\[[g]*[f] = [f]*[g], \]

即

\[[g]*[\alpha]*[\beta^-] = [\alpha]*[\beta^-]*[g], \]

两边同时左乘 \([\alpha^-]\) 并右乘 \([\beta]\) 得

\[[\alpha^-]*[g]*[\alpha] = [\beta^-]*[g]*[\beta]. \]

即 \(\hat{\alpha} = \hat{\beta}\)。

Definition 5.54（单连通）称空间 \(X\) 单连通如果它道路连通且 \(\pi_1(X, x_0)\) 是单元素群。此时也记 \(\pi_1(X, x_0) = 0\)。

Exercise 5.55 称 \(A\subset \mathbb R^n\) 是星型集合如果对某个点 \(a_0\in A\)，任意从 \(a_0\) 到 \(A\) 中其他点的直线段都包含于 \(A\)。证明若 \(A\) 是星型集合，则 \(A\) 单连通。

Proof：对任意 \(a_1, a_2\in A\)，令 \(f = [a_1, a_0]\circ [a_0, a_2]\)，则 \(f\subset A\)。因此 \(A\) 道路连通。

任取 \(A\) 中起点为 \(a_0\) 的环路 \(f\)，令 \(H(s, t) = (1-s)a_0 + sf(t)\)，则 \(H\) 是单点到 \(f\) 的道路同伦。即 \(A\) 是可缩空间。因此 \(\pi_1(A, a_0) = 0\)，\(A\) 单连通。

Lemma 5.56 在单连通空间 \(X\) 中，任意两条起点与终点相同的路径都同伦。

Proof：令 \(\alpha\) 和 \(\beta\) 是 \(x_0\) 到 \(x_1\) 的两条路径。则 \(\alpha * \beta^-\) 是以 \(x_0\) 为起点的环路。由 Definition 5.54，\(\alpha * \beta^- \cong e_{x_0}\)。因此

\[[\alpha*\beta^-]*[\beta] = [e_{x_0}]*[\beta] \]

即 \([\alpha] = [\beta]\)。

Notation 4 假设 \(h: X\to Y\) 是连续映射，\(h(x_0) = y_0\)，则记

\[h: (X, x_0) \to (Y, y_0). \]

Definition 5.57（连续映射诱导同态）连续映射 \(h: (X, x_0) \to (Y, y_0)\) 诱导的基于 \(x_0\) 的同态，记作

\[(h_{x_0})_* : \pi(X, x_0)\to \pi(Y, y_0) \]

定义为

\[(h_{x_0})_*([f]) = [h\circ f]. \]

在不会引起混淆的情况下，也将 \((h_{x_0})_*\) 简写为 \(h_*\)。

Exercise 5.58 对 \(A\subset X\)，令 \(r: X\to A\) 为 \(X\) 到 \(A\) 的拉回，即连续映射使得 \(\forall a\in A, r(a) = a\)。若 \(a_0\in A\)，证明诱导同态 \(r_*: \pi_1(X, a_0) \to \pi_1(A, a_0)\) 是满射。

Proof：设 \(f\) 是 \(A\) 中基于 \(a_0\) 的环路，则 \(r\circ f = f\)。即 \(f\in \text{Im} r_*\)。因此 \(r_*\) 是满射。

Theorem 5.59 若映射 \(h: (X, x_0)\to (Y, y_0)\) 和 \(k: (Y, y_0)\to (Z, z_0)\) 连续，则

\[(k\circ h)_* = k_*\circ h_*. \]

若 \(i: (X, x_0)\to (X, x_0)\) 是恒等映射，则 \(i_*\) 是恒等同态。

Exercise 5.60 设 \(h: (A, a_0)\to (Y, a_0)\) 是连续映射，\(A\subset \mathbb R^n\)。证明若 \(h\) 可被延拓为 \(\mathbb R^n\) 到 \(Y\) 的连续映射，则 \(h_*\) 是平凡同态。

Proof：对 \(Y\) 中任意基于 \(a_0\) 的环路 \(f\)，设 \(h\) 可延拓为 \(\tilde h: \mathbb R^n \to Y\)，则 \(\tilde h\circ f\) 是 \(\mathbb R^n\) 中基于 \(a_0\) 的环路。因此 \(h_*\subset \pi_1(\mathbb R^n, a_0) = 0\)。即 \(h_* = 0\)。

Corollary 5.61 若 \(h: (X, x_0)\to (Y, y_0)\) 是 \(X\) 到 \(Y\) 的同胚，则 \(h_*\) 是 \(\pi(X, x_0)\) 到 \(\pi(Y, y_0)\) 的同构。

Proof：令 \(k: (Y, y_0)\to (X, x_0)\) 是 \(h\) 的逆映射。易证 \(k_*\) 是 \(h_*\) 的逆映射。

Exercise 5.62 证明若 \(X\) 道路连通，则由连续映射诱导的同态和基点无关。更准确地，设 \(h: X\to Y\) 是连续映射，\(h(x_0) = y_0, h(x_1) = y_1\)。若 \(\alpha\) 是 \(x_0\) 到 \(x_1\) 的路径，\(\beta = h\circ \alpha\)，证明

\[\hat\beta \circ (h_{x_0})_* = (h_{x_1})_*\circ \hat\alpha. \]

Proof：

\[\begin{aligned} & ((h_{x_0})_*\circ \hat\alpha)([f]) \\ = & (h_{x_0})_*([\alpha^-]*[f]*[\alpha]) \\ = & [h\circ \alpha^-] * [h\circ f] * [h\circ \alpha] \\ = & [\beta^-]*[h\circ f]*[\beta] \\ = & \hat\beta([h\circ f]) \\ = & \hat\beta\circ (h_{x_0})_*. \end{aligned} \]