应用拓扑讲义整理 Chapter1.点集拓扑

1.1 拓扑空间

1.1.2 引入：连续映射的构造，拓扑基

Definition 1.16 称函数 \(f: \mathbb{R}\rightarrow \mathbb{R}\) 在 \(a\) 连续，如果

\[\forall \epsilon>0, \exists \delta>0, s.t. |x-a|<\delta \Rightarrow |f(x)-f(a)|<\epsilon. \]

Definition 1.17 称函数 \(f: \mathbb{R}^n\rightarrow \mathbb{R}^m\) 在 \(x=a\) 连续，如果

\[\forall \epsilon>0, \exists \delta>0, s.t. f(B(a,\delta))\subset B(f(a),\epsilon). \]

其中，\(B(p,r) = \{x\in \mathbb{R}^n: \Vert x-p\Vert_2<r\}\)/

Definition 1.18 设 \(X\subset \mathbb{R}^n, Y\subset \mathbb{R}^m\)。称函数 \(f: X\rightarrow Y\) 在 \(x=a\) 连续，如果

\[\forall \epsilon>0, \exists \delta>0, s.t. f(V_\alpha)\subset U_\alpha, \]

其中，\(V_a = B(a,\delta)\cap X, U_a = B(f(a),\epsilon)\cap Y\)。

Definition 1.19 称函数 \(f: X\rightarrow Y\) 连续如果 \(f\) 在 \(X\) 的所有点处均连续。

Example 1.20 函数 \(x\mapsto\frac 1x\) 在不含 \(0\) 的区间上连续，但在含 \(0\) 的区间上不连续。

Definition 1.21 设 \(X\subset \mathbb{R}^n, Y\subset \mathbb{R}^m\)。函数 \(f: X\rightarrow Y\) 连续如果

\[\forall U_a\in \gamma_Y. \exists V_a\in \gamma_X, s.t. f(V_a)\subset U_a, \]

其中 \(\gamma_X\) 和 \(\gamma_Y\) 分别是全体开球与 \(X\) 和 \(Y\) 的交集的集族。即

\[\gamma_X = \{B(a,\delta)\cap X: a\in X, \delta\in \mathbb{R}^+\},\gamma_Y = \{B(f(a),\epsilon)\cap X: f(a)\in Y, \epsilon\in \mathbb{R}^+\} \]

Definition 1.22（拓扑基）称集族 \(\mathcal{B}\) 为集合 \(X\) 的拓扑基，如果

• \(\cup B = X\)
• \(\forall U,V\in \mathcal{B}, \exists x\in U\cap V, B\in \mathcal{B}, s.t. x\in B\subset U\cap V\)

Definition 1.23（带拓扑基的集合上的连续性）设 \(X,Y\) 的拓扑基分别为 \(\mathcal{B}_X,\mathcal{B}_Y\)，称满射 \(f: X\rightarrow Y\) 连续，如果

\[\forall U\in \mathcal{B}_Y, \exists V\in \mathcal{B}_X, s.t. f(V)\subset U. \]

Lemma 1.24 若满射 \(f: X\rightarrow Y\) 在 Definition 1.18 和 Definition 1.19 的定义下连续，则它也在 Definition 1.23 的定义下连续。

Proof：由 Definition 1.22，\(\gamma_X, \gamma_Y\) 分别是 \(X,Y\) 的拓扑基。因此在 \(\mathbb{R}^n\) 上 Definition 1.18+Definition 1.19 与 Definition 1.23 等价。

Example 1.25 右射线 \(\mathcal{B}_{RR} = \{\{x: x>s\}: s\in \mathbb{R}\}\) 是 \(\mathbb{R}\) 上的一族拓扑基。

Exercise 1.26 证明 \(\mathbb{R}\) 上全体半区间 \(\mathcal{B} = \{[a,b):a<b\}\) 是一族拓扑基。

Proof：因为 \(\forall x\in \mathbb{R}\)，均有 \(x\in [x,x+1)\in \mathcal{B}\)，所以 \(\cup \mathcal{B} = \mathbb{R}\)。

设 \(a\leq c,[a,b)\cap [c,d)\neq \emptyset\)，则 \(b>c\)，因此 \([a.b)\cap [c,d) = [a,\min\{b,d\})\in \mathcal{B}\)。故 \(\forall x\in [a,b)\cap [c,d), x\in [a,\min\{b,d\})\in \mathcal{B}\)。

Example 1.27 \(\mathbb{R}^2\) 上的一族拓扑基是全体四分之一平面

\[\mathcal{B}_q = \{Q(r,s) = \{(x,y)\in \mathbb{R}^2: x>r, y>s\}: r,s\in \mathbb{R}\}. \]

Exercise 1.28 设 \(\mathbb{R}^2\) 上的开正方形为

\[S((a,b),d) = \{(x,y): \max\{|x-a|,|y-b|\}<d\}. \]

证明 \(\forall (m,n)\in \mathbb{R}^2, d>0\)，\(\forall (a,b)\in S((m,n),d), \exists r>0, s.t. S((a,b),r)\subset S((m,n),d)\)，且 \(\mathbb{R}^2\) 上的全体开正方形

\[\mathcal{B}_s = \{S((a,b),d): (a,b)\in\mathbb{R}^2, d>0\} \]

是 \(\mathbb{R}^2\) 上的一族基。

Proof：设 \((m,n)\in \mathbb{R}^2, d>0\)，令 \(\delta = \min\{a-(m-d),(m+d)-a,b-(n-d),(n+d)-b\}\)，则

\[\forall (u,v)\in S((a,b),\delta), |u-m|<|m-a|+d-|m-a|<d, |v-n|<|n-b|+d-|n-b|<d. \]

因此 \(S((a,b),\delta)\subset S((m,n),d)\)。

下面证明 \(\mathcal{B}_s\) 是 \(\mathbb{R}^2\) 上的一族基。因为

\[\forall (x,y)\in \mathbb{R}^2, (x,y)\in S((a,b),1)\in \mathcal{B}_s, \]

所以 \(\cup \mathcal{B} = \mathbb{R}^2\)。

设 \(S((a_1,b_1),d_1),S((a_2,b_2),d_2)\in \mathcal{B}_s, (x,y)\in S((a_1,b_1),d_1)\cap S((a_2,b_2),d_2)\)

令 \(d = \{\min\{x-(a_i-d_i),(a_i+d_i)-x,y-(b_i-d_i),(b_i+d_i)-y: i=1,2\}\)，则 \(d>0\) 且 \(S((x,y).d)\subset S((a_1,b_1),d_1)\cap S((a_2,b_2),d_2)\)。

所以 \(\mathcal{B}_s\) 是 \(\mathbb{R}^2\) 上的一族基。

Exercise 1.29 证明闭球集

\[\overline{B}(p,r) = \{x\in \mathbb{R}^n: \Vert x-p\Vert_2\leq r\} \]

不是 \(\mathbb{R}^n\) 上的基，但

\[\mathcal{B}_p = \{\overline{B}(a,r): a\in \mathbb{R}^n, r\geq 0\} \]

即全体闭球和单点集的集族是基。

Proof：考虑 \(B(0,1)\) 和 \(B(2e_1,1)\)（\(e_1 = (1,0,\dots,0)\)），因为 \(B(0,1)\cap B(2e_1,1) = \{e_1\}\)，且对任意 \(r>0\)，\((1+r)e_1\in \overline{B}(e_1,r)\) 且 \((1+r)e_1\notin \{e_1\}\)，所以全体闭球不是 \(\mathbb{R}^n\) 上的基。

因为 \(\forall x\in \mathbb{R}^n, x\in B(x,0)\)，且

\[\forall B(x_1,r_1),B(x_2,r_2)\in \mathcal{B}_p, x\in B(x_1,r_1)\cap B(x_2,r_2), x\in B(x,0)\subset B(x_1,r_1)\cap B(x_2,r_2), \]

所以 \(\mathcal{B}_p\) 是 \(\mathbb{R}^n\) 上的基。

1.1.3 开集：从拓扑基到拓扑

Definition 1.30 称 \(U\subset X\) 是（相对给定拓扑基 \(\mathcal{B}\) 的）开集，如果

\[\forall x\in U, \exists B\in \mathcal{B}, s.t. x\in B\subset U. \]

Lemma 1.31 \(\mathcal{B}\) 上的每个邻域都是开集。

Proof：\(B\subset B\in \mathcal{B}\)。

Exercise 1.32 右射线对应的开集族是什么？

Solution：根据 Definition 1.30，开集是右射线之并。而右射线之并仍为右射线。因此 \(\mathcal{B}_{RR}\) 对应的开集族也是 \(\mathcal{B}_{RR}\)。

Lemma 1.33 两个开集的交仍为开集。

Proof：设 \(U_1\) 和 \(U_2\) 是开集，任意给定 \(x\in U_1\cap U_2\)，则由 Definition 1.30 得

\[\exists B_1, B_2\in \mathcal{B}, s.t. x\in B_1\subset U_1, x\in B_2\subset U_2. \]

由 Definition 1.22，存在 \(B_3\in \mathcal{B}\) 使得 \(x\in B_3\subset B_1\cap B_2\)。

故 \(U_1\cap U_2\) 是开集。

Lemma 1.34 两个开集的并是开集。

Lemma 1.35 任意多个开集的并是开集。

Definition 1.36（拓扑）称 \(X\) 由拓扑基 \(\mathcal{B}\) 生成的拓扑 \(\mathcal{T}\) 为 \(X\) 上由 Definition 1.30 定义的全体开集。

Definition 1.37（\(\mathbb{R}^n\) 上的标准拓扑）称 \(\mathbb{R}^n\) 上的标准拓扑为由 \(\mathbb{R}^n\) 上全体开球生成的拓扑。

Theorem 1.38 \(X\) 上由一组基生成的拓扑满足

• \(\emptyset, X\in \mathcal{T}\)
• \(\alpha\subset \mathcal{T}\Rightarrow \cup_{U\in \alpha} U\in \mathcal{T}\)
• \(U,V\in \mathcal{T}\Rightarrow U\cap V\in \mathcal{T}\)

Proof：Definition 1.30 + Lemma 1.33 + Lemma 1.35

Example 1.39

• \(X\) 上最大的拓扑基是 \(X\) 的幂集 \(\mathcal{B}_d = \{A\subset X\} = 2^X\)，称为离散拓扑，它是由单点基 \(\mathcal{B}_s(X) = \{\{x\}: x\in X\}\) 生成的。
• \(X\) 上最小的拓扑基是 \(\{\emptyset, X\}\)，称为平凡拓扑，它是由 \(\{X\}\) 生成的。

Exercise 1.40 证明：若 \(U\) 相对拓扑基 \(\mathcal{B}\) 是开集，则 \(\mathcal{B}\cup \{U\}\) 仍为拓扑基。

Proof：显然 \(\cup(\mathcal{B}\cup \{U\})\supset \cup \mathcal{B} = X\)。

设 \(x\in B\cap U\)，其中 \(B\in \mathcal{B}\)。因为 \(B\) 是开集，所以 \(B\cap U\) 也是开集。根据 Definition 1.30，存在 \(B_x\in \mathcal{B}\) 使得 \(x\in B_x\subset B\cap U\)。因此 \(B\cup\{U\}\) 是拓扑基。

1.1.4 拓扑空间：从拓扑到拓扑基

Definition 1.41（拓扑）对任意集合 \(X\)，称 \(X\) 的一族子集 \(\mathcal{T}\) 为 \(X\) 上的拓扑，如果

• \(\emptyset, X\in \mathcal{T}\)
• \(\alpha\subset \mathcal{T}\Rightarrow \int_{U\in\alpha}\in \mathcal{T}\)
• \(U,V\in \mathcal{T}\Rightarrow U\cap V\in \mathcal{T}\)

称 \((X,\mathcal{T})\) 为拓扑空间，\(\mathcal{T}\) 中集合为开集。

Corollary 1.42 Definition 1.36 定义的由一族拓扑基 \(\mathcal{B}\) 生成的拓扑在 Definition 1.41 下也是拓扑。

Proof：Theorem 1.38。

Example 1.43 对任意 \(n\in \mathbb{Z}\)，定义

\[B(n) = \begin{cases} \{n\}, & n\text{ is odd,} \\ \{n-1,n,n+1\}, & n\text{ is even.} \end{cases} \]

称 \(\mathcal{B} = \{B(n): n\in \mathbb{Z}\}\) 生成的拓扑为整数数轴。

Theorem 1.44 由拓扑基 \(\mathcal{B}\) 生成的拓扑等于 \(\mathcal{B}\) 中元素的任意并所成集族。

Proof：由 Lemma 1.31，\(\mathcal{B}\) 中元素的任意并是开集。

反之，设 \(U\in \mathcal{T}\)，因为对任意 \(x\in U\)，存在 \(B_x\in \mathcal{B}\) 使得 \(x\in B_x\subset U\)，所以 \(U = \cup_{x\in U} B_x\) 是 \(\mathcal{B}\) 中元素之并。

Corollary 1.45 设 \(\mathcal{T}\) 是 \(X\) 由拓扑基 \(\mathcal{B}\) 生成的拓扑，且 \(\mathcal{B}\) 的元素可以由 \(\mathcal{B'}\) 生成，则 \(\mathcal{T}\) 中所有开集 \(U\in \mathcal{T}\) 是 \(\mathcal{B'}\) 中元素之并。

Lemma 1.46 设 \((X,\mathcal{T})\) 是拓扑空间，且一族开集 \(C\subset \mathcal{T}\) 满足

\[\forall U\in \mathcal{T}, \forall x\in U, \exists C\in \mathcal{C}, s.t. x\in C\subset U, \]

则 \(\mathcal{C}\) 是 \(\mathcal{T}\) 的一族基。

Proof：先证明 \(\mathcal{C}\) 是拓扑基。

在题设中令 \(U=X\) 得 \(\cup\mathcal{C} = X\)。

设 \(x\in C_1\cap C_2, C_1,C_2\in \mathcal{C}\)。因为 \(C_1,C_2\) 是开集，所以存在 \(C_3\in \mathcal{C}\) 使得 \(x\in C_3\subset C_1\cap C_2\)。

因此由 Definition 1.22，\(\mathcal{C}\) 是一族基。

下证由 \(\mathcal{C}\) 生成的拓扑 \(\mathcal{T}'\) 就是 \(\mathcal{T}\)。

对任意 \(U\in \mathcal{T}, x\in U\)，存在 \(C\in \mathcal{C}\) 使得 \(x\in C\subset U\)。根据 Definition 1.30 和 Definition 1.36，有 \(U\in \mathcal{T}'\)。

另一方面，根据 Corollary 1.45，任意 \(W\in \mathcal{T}'\) 都是 \(\mathcal{C}\) 中一族元素之并。而因为 \(\mathcal{C}\subset \mathcal{T}\)，所以 \(W\in \mathcal{T}\)。

Example 1.47 可数集族

\[\mathcal{B} = \{(a,b): a<b, a,b\in \mathbb{Q}\} \]

是一族拓扑基，且生成 \(\mathbb{R}\) 上的标准拓扑。

Lemma 1.48 \(X\) 的一族子集是拓扑当且仅当它生成自身。

Proof：根据拓扑的第 1、3 条定义知拓扑生成自身。下证充分性。

设 \(\mathcal{T}\) 生成自身，则 \(\mathcal{T}\) 满足 1 和 3。

设 \(U,V\in \mathcal{T}\)，根据 Definition 1.30，\(U\cup V\) 是开集，即 \(u\cup V\in \mathcal{T}\)。且该结论对任意并也成立。

因此 \(\mathcal{T}\) 满足 2，故是拓扑。

1.1.5 连续映射

Definition 1.49 称 \(U\subset Y\) 在映射 \(f: X\subset Y\) 的原像为

\[f^{-1}(U) = \{x\in X: f(x)\in U\}. \]

Exercise 1.50 证明 \(f^{-1}\) 是保包含、并、交、差运算的：

\[\begin{aligned} B_0\subset B_1&\Rightarrow f^{-1}(B_0)\subset f^{-1}(B_1), \\ f^{-1}(B_0\cup B_1) &= f^{-1}(B_0)\cup f^{-1}(B_1), \\ f^{-1}(B_0\cap B_1) &= f^{-1}(B_0)\cap f^{-1}(B_1), \\ f^{-1}(B_0\backslash B_1) &= f^{-1}(B_0)\backslash f^{-1}(B_1). \\ \end{aligned} \]

但 \(f\) 只保包含、并运算：

\[\begin{aligned} A_0\subset A_1&\Rightarrow f(A_0)\subset f(A_1), \\ f^{-1}(A_0\cup A_1) &= f(A_0)\cup f(A_1), \\ f^{-1}(A_0\cap A_1) &\subset f(A_0)\cap f(A_1), \\ f^{-1}(A_0\backslash A_1)&\supset f(A_0)\backslash f(A_1). \\ \end{aligned} \]

最后两个包含关系取等如果 \(f\) 是单射。

Proof：

• 设 \(B_0\subset B_1, y\in B_0\)，则 \(\forall x\in f^{-1}(y), f(x) = y\in B_0\subset B_1\)，即 \(x\in f^{-1}(B_1)\)。因此 \(f^{-1}(B_0) = \cup_{y\in B_0} f^{-1}(y) \subset f^{-1}(B_1)\)。

• 设 \(y\in B_0\cup B_1\)，则 \(y\in B_0\) 或 \(y\in B_1\)。即 \(f^{-1}(y)\subset f^{-1}(B_0)\) 或 \(f^{-1}(y)\subset f^{-1}(B_1)\)。因此 \(f^{-1}(B_0\cup B_1) = \cup_{y\in B_0\cup B_1}\subset f^{-1}(B_0)\cup f^{-1}(B_1)\)；

  设 \(x\in f^{-1}(B_0)\cup f^{-1}(B_1)\)，则 \(x\in f^{-1}(B_0)\) 或 \(x\in f^{-1}(B_1)\)，即 \(f(x)\in B_0\) 或 \(f(x)\in B_1\)，即 \(f(x)\in B_0\cup B_1\)。因此 \(x\in f^{-1}(B_0\cup B_1)\)，因此 \(f^{-1}(B_0)\cup f^{-1}(B_1) \subset f^{-1}(B_0\cup B_1)\)。

• 设 \(y\in B_0\cap B_1\)，则 \(y\in B_0\) 且 \(y\in B_1\)。即 \(f^{-1}(y)\subset f^{-1}(B_0)\) 且 \(f^{-1}(y)\subset f^{-1}(B_1)\)。因此 \(f^{-1}(B_0\cap B_1) = \cup_{y\in B_0\cap B_1}\subset f^{-1}(B_0)\cap f^{-1}(B_1)\)；

  设 \(x\in f^{-1}(B_0)\cap f^{-1}(B_1)\)，则 \(x\in f^{-1}(B_0)\) 或 \(x\in f^{-1}(B_1)\)，即 \(f(x)\in B_0\) 且 \(f(x)\in B_1\)，即 \(f(x)\in B_0\cap B_1\)。因此 \(x\in f^{-1}(B_0\cap B_1)\)，因此 \(f^{-1}(B_0)\cap f^{-1}(B_1) \subset f^{-1}(B_0\cap B_1)\)。

• 先证明 \(f^{-1}(B^c) = f^{-1}(B)^c\)。设 \(y\in B^c,x\in f^{-1}(y)\)，则 \(f(x)\notin B\)，因此 \(x\notin f^{-1}(B)\)，因此 \(f^{-1}(B^c)\subset f^{-1}(B)^c\)。反之，设 \(x\in f^{-1}(B)^c\) 即 \(f(x)\notin B\)，则 \(f(x)\in B^c, x\in f^{-1}(B^c)\)。故 \(f^{-1}(B)^c\subset f^{-1}(B^c)\)。

  \(f^{-1}(B_0\backslash B_1) = f^{-1}(B_0\cap B_1^c) = f^{-1}(B_0)\cap f^{-1}(B_1^c) = f^{-1}(B_0)\cap f^{-1}(B_1)^c = f^{-1}(B_0)\backslash f^{-1}(B_1)\)。

反之：

• 设 \(A_0\subset A_1\)，则 \(\forall x\in A_0\subset A_1, f(x)\in f(A_1)\)。因此 \(f(A_0)\subset f(A_1)\)。

• 设 \(y\in f(A_0\cup A_1)\)，则 \(\exists x\in A_0\cup A_1, f(x)=y\)。\(x\in A_0\) 或 \(x\in A_1\)，故 \(y\in f(A_0)\) 或 \(y\in f(A_1)\)。

  反之，对任意 \(y\in f(A_0)\cup f(A_1)\)，若 \(y\in f(A_0)\)，则存在 \(x\in A_0\subset A_0\cup A_1\) 使得 \(f(x) = y\)，因此 \(y\in f(A_0\cup A_1)\)。\(y\in f(A_1)\) 同理。因此 \(f(A_0)\cup f(A_1)\subset f(A_0\cup A_1)\)。

• 设 \(y\in f(A_0\cap A_1)\)，则 \(\exists x\in A_0\cap A_1,f(x)=y\)。\(x\in A_0\) 且 \(x\in A_1\)，故 \(y\in f(A_0)\) 且 \(y\in f(A_1)\)。因此 \(f(A_0\cap A_1)\subset f(A_0)\cap f(A_1)\)。

  反之不成立，例如 \(f(x) = x^2, A_0 = (-1,0), A_1 = (0,1),f(A_0\cap A_1) = \emptyset, f(A_0)\cap f(A_1) = (0,1)\)。

• 设 \(y\in f(A_0)\backslash f(A_1)\)，则 \(\exists x\in A_0\) 使得 \(f(x) = y\)。若 \(x\in A_1\)，则 \(f(x)\in f(A_1)\) 矛盾，故 \(x\in A_0\backslash A_1\)。因此 \(f(A_0\backslash A_1)\supset f(A_0)\backslash f(A_1)\)。

  反之不成立，例如 \(f(x) = x^2, A_0 = (-1,1), A_1 = (0,1), f(A_0\backslash A_1) = [0,1), f(A_0)\backslash f(A_1) = \{0\}\)。

当 \(f\) 是单射时，令 \(g = f^{-1}\bigg|_{f(X)}\) 即可。

Lemma 1.51 设映射 \(f: X\rightarrow Y, A\subset X, B\subset Y\)，则

\[A\subset f^{-1}(f(A)), f(f^{-1}(B))\subset B. \]

其中第一个包含关系取等如果 \(f\) 是单射；第二个包含关系取等如果 \(g\) 是满射或 \(B\subset f(X)\)。

Proof：由原像集的定义知 \(a\in A\Rightarrow a\in f^{-1}(f(A))\)。

反之，若 \(a\in f^{-1}(f(A))\)，则 \(f(a)\in f(A)\)。当 \(f\) 为单射时，可以推知 \(a\in A\)。

由原像集的定义知 \(b\in B\Rightarrow b\in B\)。

反之，若 \(f\) 是满射或 \(B\subset f(X)\)，则对任意 \(b\in B\) 有 \(f^{-1}(\{b\})\neq \emptyset\)，故

\[b\in f(f^{-1}\{b\})\subset f(f^{-1}(B)). \]

Definition 1.52（拓扑空间的连续映射）称函数 \(f: X\rightarrow Y\) 连续如果 \(Y\) 中任意开集 \(U\subset Y\) 的原像都是 \(X\) 中开集。

Lemma 1.53 设 \(f: X\rightarrow Y\) 是如 1.52 定义的连续映射，则开集 \(U\subset Y\) 的原像满足

\[f^{-1}(U) = \cup_{x\in X}V_x, \]

其中 \(V_x\) 是 \(X\) 的拓扑基的元素，且满足 \(f(V_x)\subset U\)。

Proof：因为 \(U\) 是开集，所以由 Definition 1.52 知 \(f^{-1}(U)\) 是开集。

根据 Definition 1.30，由 \(x\in f^{-1}(U)\) 得存在 \(V_x\in \mathcal{B}_X\) 使得 \(x\in V_x\subset f^{-1}(U)\)。

因此 \(f^{-1}(U) \subset \cup_{x\in X} V_x\)。

反之，因为 \(f(V_x)\subset U\)，所以由 Exercise 1.50(1) 得 \(f^{-1}f(V_x)\subset f^{-1}(U)\)。再由 Lemma 1.51 得 \(V_x\subset f^{-1}(U)\)。因此 \(\cup_{x\in X}V_x\subset f^{-1}(U)\)。

Theorem 1.54 若满射在 Definition 1.52 的定义下连续，则它也在 Definition 1.23 的定义下连续。

Proof：考虑 \(U\in \mathcal{B}_Y\)，根据 Lemma 1.31，\(U\) 是开集。由 Definition 1.52，\(f^{-1}(U)\) 是 \(X\) 中开集。因为 \(f\) 是满射，所以 \(f^{-1}(U)\) 非空。由 Definition 1.30 有

\[\forall x\in f^{-1}(U), \exists V\in \mathcal{B}_X, s.t. x\in V\subset f^{-1}(U), \]

即 \(f(V)\subset f(f^{-1}(U)) = U\)。

Exercise 1.55 证明 Lemma 1.53 对如下改进的 Definition 1.23 定义下的连续函数成立：

\[\begin{aligned} \forall U\in \mathcal{B}_Y, \forall x\in X, s.t. f(x)\in U, \\ \exists V\in \mathcal{B}_X, x\in V, f(V)\subset U. \\ \end{aligned} \]

Proof：设 \(U\subset Y\) 为 \(Y\) 中开集。则由 Theorem 1.44 知

\[U = \cup_{y\in U} B_y, y\in B_y\in \mathcal{B}_Y. \]

由题设知

\[\forall B_y, \forall x,s.t. f(x)\in U_y, \exists V_{x,y}\in \mathcal{B}_{X,y}, x\in V_x, f(V)\subset B_y. \]

令 \(V_x = \cup_yV_{x,y}\)，则 \(f^{-1}(U) = \cup_{x\in X} V_x\)。Lemma 成立。

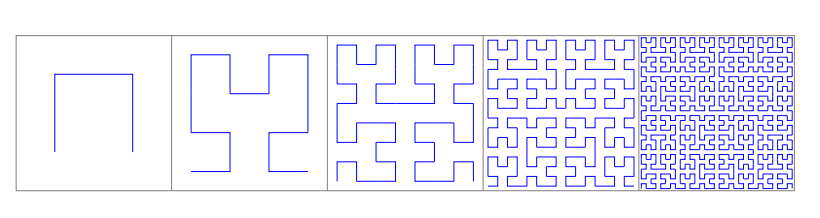
Example 1.56 连续函数不一定有良好的形态，例如 Hilbert 曲线

1.1.6 子拓扑基

Definition 1.57（子拓扑基）\(X\) 上的子拓扑基 \(\mathcal{S}\) 是 \(X\) 中的一族满足 \(\cup_\mathcal{S}B = X\) 的子集。

Example 1.58 全体半径大于 \(h>0\) 的开球所成集族（记作 \(\mathcal{B}_h\)）是一族子拓扑基，但不是拓扑基。

Definition 1.59（由子拓扑基生成的拓扑）定义子拓扑基 \(\mathcal{S}\) 生成的拓扑 \(\mathcal{T_S}\) 为 \(\mathcal{S}\) 中元素有限交的任意并所成集族。

Exercise 1.60 证明按 Definition 1.50 定义的由子拓扑基 \(\mathcal{S}\) 生成的拓扑也是由 Definition 1.41 定义的拓扑。

Proof：\(\emptyset\in \mathcal{T_S}\)。因为 \(\cup_\mathcal{S}B = X\)，所以 \(X\in \mathcal{T_S}\)。

设 \(U,V\in \mathcal{T_S}\)，则 \(U=\cup_{i\in I}\cap_{j=1}^{n_i} U_{i,j}, V=\cup_{i'\in I'}\cap_{j'=1}^{n_{j'}}V_{i',j'}\)。则

\[U\cap V = \cup_{i\in I,i'\in I'}\cap_{j,j'}(U_{i,j}\cap V_{i',j'})\in \mathcal{T_S}, \]

设 \(\{U_\alpha\}\subset \mathcal{T_S}\)，则

\[\cup_{\alpha}U_\alpha = \cup_\alpha\cup_{i\in I_\alpha}\cap_{j=1}^{n_{i,\alpha}} U_{i,j,\alpha} \in \mathcal{T_S}. \]

因此 \(\mathcal{T_S}\) 是拓扑。

Exercise 1.61 证明 \(\mathcal{S}\subset \mathcal{T_S}\)，即由子拓扑基 \(\mathcal{S}\) 生成的拓扑中，\(\mathcal{S}\) 中所有元素都是 \(X\) 中开集。

Proof：在 \(U = \cup_{i\in I}\cap_{j=1}^{n_i}U_{i,j}\) 中的并集和交集运算中都只取一项即可。

Exercise 1.62 证明若 \(\mathcal{T}\) 是 \(X\) 中拓扑且 \(\mathcal{S}\subset \mathcal{T}\)，则 \(\mathcal{T_S}\subset \mathcal{T}\)。

Proof：因为 \(\mathcal{T}\) 对任意并和有限交运算封闭，所以 \(\mathcal{S}\subset \mathcal{T}\Rightarrow \mathcal{T_S}\subset \mathcal{T}\)。

Exercise 1.63 假设对任意 \(x\in X\)，\(x\) 包含于至多有限个 \(\mathcal{S}\) 中集合。令 \(B_x = \cap_{x\in B\in \mathcal{S}}B\)，证明

• \(\mathcal{B_S} := \{B_x: x\in X\}\) 是 \(\mathcal{T_S}\) 的一族拓扑基。
• 若 \(\mathcal{B}\) 是 \(\mathcal{T_S}\) 的一族基，则 \(\mathcal{B_S}\subset \mathcal{B}\)。

Proof：根据子基拓扑的定义得

\[\mathcal{T_S} = \left\{\bigcup_{i\in I} (S_{i1}\cap S_{i2}\cap\dots\cap S_{ik_I})\bigg| S_{ij}\in \mathcal{S}, k_i\in \mathbb{N}\right\} \]

• 由定义，有

  \[\mathcal{T(B_S)} = \left\{ B_x = \bigcup_{x\in J}(S_{x1}\cap S_{x2}\cap\dots\cap S_{xk_x})\bigg|x\in S_{jk}\in \mathcal{S}\right\} \]

  所以 \(\mathcal{T(B_S)} \subset \mathcal{T_S}\)。

  反之，对任意开集 \(U\in \mathcal{T_S}, \forall x\in U, U\subset \cup_xB_x\subset \mathcal{T(B_S)}\)，所以 \(\mathcal{T_S}\subset \mathcal{T(B_S)}\)。

  因此，\(\mathcal{T_S} = \mathcal{T(B_S)}\)。

• 因为 \(\mathcal{B}\) 是 \(\mathcal{T_S}\) 的一族基，所以

  \[\forall x\in X, \exists U = \bigcup_{i\in I} B_i\subset \mathcal{B}\subset \mathcal{T_S},s.t.x\in U. \]

  又因为 \(B_x\) 是 \(\mathcal{T_S}\) 中包含 \(x\) 的最小集合，所以 \(B_x\subset \cup_{i\in I} B_i\)。所以 \(\mathcal{B_S}\subset \mathcal{B}\)。

1.1.8 闭集

Definition 1.66 \(X\) 的子集称为闭集如果它的补集是开集。

Example 1.67 集合

\[K = \{\frac 1n: n\in \mathbb{Z}^+\} \]

是非开非闭的。但 \(K\cup \{0\}\) 是闭的。

Theorem 1.68 \(X\) 的闭子集族 \(\sigma\) 满足

• \(\emptyset, X\in \sigma\)
• \(\alpha\subset \sigma \Rightarrow \cap\alpha\in \sigma\)
• \(U,V\in \sigma \Rightarrow U\cup V \in \sigma\)

Example 1.69 下面的例子说明了开集的任意交不一定是开集，闭集的任意并不一定是闭集：

\[\begin{aligned} \bigcap\left\{\left(-\frac 1n,\frac 1n\right): n=1,2,\dots\right\} &= \{0\};\\ \bigcup\left\{\left[-1+\frac 1n,1-\frac 1n\right]:n=1,2,\dots\right\} &= (-1,1). \end{aligned} \]

Lemma 1.70 函数 \(f: X\rightarrow Y\) 连续当且仅当闭集的原像是闭集。

Proof：由 Definition 1.49，有

\[f^{-1}(U) = f^{-1}(Y\backslash(Y\backslash U)) = X\backslash f^{-1}(Y\backslash U). \]

因此闭集 \(Y\backslash U\) 的原像 \(f^{-1}(Y\backslash U)\) 是闭集等价于开集 \(U\) 的原像 \(X\backslash f^{-1}(Y\backslash U)\) 是开集。

Definition 1.71（函数图像）函数 \(f: X\rightarrow Y\) 的图像是集合

\[\{(x,y)\in X\times Y: y=f(x)\}. \]

Lemma 1.72 连续函数 \(f: [a,b]\rightarrow \mathbb{R}\) 在集合 \([a,b]\times \mathbb{R}\) 上是闭集。

Exercise 1.73 给出不连续函数 \(f: \mathbb{R}\rightarrow \mathbb{R}\) 的例子，其图像在 \(\mathbb{R}^2\) 上是闭集/不是闭集。

Solution：令 \(f(x) = D(x)\) 为 Dirichlet 函数（即，在有理数为 1，无理数为 0），则其图像在 \(\mathbb{R}^2\) 上是非闭集；令

\[f(x) = \begin{cases} \sin \frac 1x. &x\neq 0; \\ 0, &x=0, \end{cases} \]

其图像在 \(\mathbb{R}^2\) 上的闭集。

Exercise 1.74 设 \(X\) 是拓扑空间，

• 对连续函数 \(f: X\rightarrow \mathbb{R}\)，证明集合 \(\{x\in X: f(x)=r\}\) 即 \(f(x)=r\) 的解集为闭集。
• 证明当 \(Y\) 为任意拓扑空间时，\(f:X\rightarrow Y\) 不满足上述性质。
• \(Y\) 需要满足什么性质可以保证上述结论成立？

Proof：因为 \(\{r\}\) 是 \(\mathbb{R}\) 中闭集，所以原像集 \(f^{-1}(\{r\})\) 是闭集。

若 \(Y\) 是平凡拓扑，则 \(\{f(x)=r\}\) 不是闭集。

结论正确需要满足 \(Y\) 的单点集为闭集。

1.1.9 内部和外部

Definition 1.75（内部）称点 \(x\in X\) 是 \(A\) 的内部点如果它的某个邻域 \(W\) 完全包含在 \(A\) 中。\(U\) 的全体内部点所成集合记为 \(\text{Int}(U)\)。

Lemma 1.76 对任意集合 \(A\)，\(\text{Int}(A)\) 是开集。

Proof：对任意 \(x\in \text{Int}(A)\)，存在开集 \(W_x\) 使得 \(x\in W_x\subset \text{Int}(A)\)，因此 \(\text{Int}(A) = \cup_x W_x\) 为开集。

Example 1.77 闭球的内部是对应开球。

Definition 1.78（外部）称点 \(x\in X\) 是 \(A\) 的外部点如果它的某个邻域 \(W\) 完全包含在 \(X\backslash A\) 中。\(U\) 的全体外部点所成集合记为 \(\text{Ext}(U)\)。

Example 1.79 集合 \(K\) 的外部是 \(\mathbb{R}\backslash K\backslash \{0\}\)。

Definition 1.80（闭包点）称点 \(x\in X\) 是 \(A\) 的闭包点如果 \(x\) 的每个邻域都包含 \(A\) 中的点。

Example 1.81 \(K\) 的闭包点集是 \(K\cup \{0\}\)。

Definition 1.82（聚点）称 \(x\) 是 \(A\) 的聚点如果 \(x\) 的每个邻域都包含 \(A\) 中非 \(x\) 的点。

Example 1.83 \(K\) 的唯一一个聚点是 \(0\)。

Example 1.84 \(\mathbb{R}\) 中所有点都是 \(\mathbb{Q}\) 的聚点。

Definition 1.85（孤立点）称 \(x\in A\) 是 \(A\) 的孤立点如果 \(x\) 的某个邻域与 \(A\backslash \{x\}\) 无交。

Example 1.86 \(K\) 的所有点都是孤立点。

Definition 1.87（边界点）称 \(x\in A\) 是 \(A\) 的边界点如果 \(x\) 同时是 \(A\) 和 \(A^c\) 的闭包点。记边界点集为 \(\text{Fr}(A)\)。

Theorem 1.88 对任意集合 \(A\subset X\)，其内部、边界和外部为 \(X\) 的一个划分。

Proof：对任意 \(a\in X\)：

• 若存在邻域 \(\mathcal{N}_a\) 满足 \(a\in \mathcal{N}_a\subset A\)，则由 Definition 1.75 得 \(a\in \text{Int}(A)\)；
• 若存在邻域 \(\mathcal{N}_a\) 满足 \(a\in \mathcal{N}_a\subset X\backslash A\)，则由 Definition 1.78 得 \(a\in \text{Ext}(A)\)；
• 否则，对任意 \(a\) 的邻域均有 \(\mathcal{N}_a\not\subset A\) 且 \(\mathcal{N}_a\not\subset X\backslash A\)。则由 Definition 1.87 的 \(a\in \text{Fr}(A)\)。

Definition 1.89（闭包）称 \(A\) 的全体闭包点为 \(A\) 的闭包，记作 \(\text{Cl}(A)\) 或 \(\overline{A}\)。

Lemma 1.90 \(\text{Int}(A)\subset A\subset \text{Cl}(A)\)。

Lemma 1.91 \(\text{Cl}(A) = \text{Int}(A)\cup \text{Fr}(A)\)。

Theorem 1.92 \(A\) 的闭包是最小的包含 \(A\) 的闭集，即

\[\text{Cl}(A) = \bigcap\{G: A\subset G, G 为 X中闭集\} \]

Proof：记 \(\alpha := \{G:A\subset G, G为X中闭集\}\)，\(A^- = \cap \alpha\)，则只需证明 \(A^-\subset \text{Cl}(A)\) 且 \(A^-\supset \text{Cl}(A)\)。

若 \(x\notin \text{Cl}(A)\)，则由 Definition 1.80 和 Definition 1.89 得，存在 \(x\) 的开邻域使得 \(\mathcal{N}_x\cap A = \emptyset\)。即 \(P := X\backslash \mathcal{N}_x\) 包含 \(A\)。因为 \(P\) 是闭集，所以 \(P\in \alpha, x\notin A^-\)。即 \(\text{Cl}(A)^c\subset (A^-)^c\)，因此 \(A^-\subset \text{Cl}(A)\)。

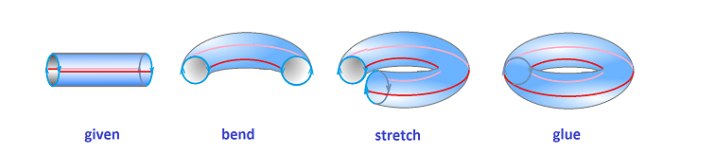
若 \(x\in \text{Cl}(A)\)，则对任意包含 \(x\) 的闭集 \(G\)，\(G^c\) 为开集且 \(G^c\cap A = \emptyset\)。若 \(x\in G^c\)，则存在 \(x\) 的邻域满足 \(\mathcal{N}_x\subset G^c\) 即 \(\mathcal{N}_x\cap A = \emptyset\)，与 \(x\in \text{Cl}(A)\) 矛盾。因此 \(\text{Cl}(A)\subset A^-\)。

Exercise 1.93 证明 \(\text{Cl}(A\cap B)\subset \text{Cl}(A)\cap \text{Cl}(B)\)。改为无限交？

Proof：设 \(x\in \text{Cl}(A\cap B)\)，则对 \(x\) 的任意一个邻域 \(\mathcal{N}_x\) 均有 \(\mathcal{N}_x\cap (A\cap B)\neq \emptyset\)，即 \(\mathcal{N}_x\cap A = \emptyset\) 且 \(\mathcal{N}_x\cap B = \emptyset\)。因此 \(x\in \text{Cl}(A)\cap \text{Cl}(B)\)。即 \(\text{Cl}(A\cap B) = \text{Cl}(A)\cap \text{Cl}(B)\)。

Theorem 1.94 \(A\) 的内部是最大的包含于 \(A\) 的开集，即

\[\text{Int}(A) = \bigcup\{U: U\subset A, U为X中开集\} \]

Theorem 1.95 设 \(A'\) 为 \(A\) 的全体聚点，则 \(\text{Cl}(A) = A\cup A'\)。

Proof：设 \(x\in \text{Cl}(A)\)。若 \(x\in A\)，则 \(x\in A\cup A'\)。

否则 \(x\neq A\)。由 Definition 1.89 得 \(x\) 的邻域至少包含 \(A\) 中的一个点。由 Definition 1.75，\(x\in A'\)。

因此 \(x\in A\cup A'\)。

Corollary 1.96 拓扑空间的子集是闭集当且仅当它包含自身的所有聚点。

Proof：若 \(A\supset A'\)，则 \(A\cap A' = A = \text{Cl}(A)\)。即 \(A\) 是闭集；

设 \(A\) 是闭集，且存在 \(x\) 是 \(A\) 的聚点但 \(x\neq A\)，则由 Definition 1.82 知 \(x\) 的任意邻域中都存在 \(p\in A, p\neq x\)。这与 \(A^c\) 是开集矛盾。

1.1.10 Hausdorff 空间

Definition 1.97（收敛） 设 \(X\) 是邻域基为 \(\gamma\) 的集合，\(\{x_n: n=1,2,\dots,\}\) 是 \(X\) 中的一个序列，\(a\in X\)。称序列 \(\{x_n\}\) 收敛于 \(a\)，记作 \(\lim_{n\rightarrow \infty} x_n = a\) 或 \(x_n\rightarrow a, n\rightarrow \infty\) 如果

\[\forall U\in \gamma, a\in U, \exists N\in \mathbb{N}^+, s.t. n>N\Rightarrow x_n\in U. \]

Example 1.98 由 Definition 1.97，当拓扑空间中的两个点”不可分“时，序列可能会同时收敛到这两个点。因此收敛只在拓扑空间的点两两可分时才能合理定义。

Exercise 1.99 证明将“邻域基”改为“拓扑”的情况下，Definition 1.97 保持不变。

Proof：因为开集是邻域基的任意并，所以若 Definition 1.97 的条件对邻域基成立，则对开集也成立。

Exercise 1.100 证明若序列在邻域基 \(\gamma\) 下收敛，则它在等价于 \(\gamma\) 的邻域基下也收敛。

Proof：序列在 \(\gamma\) 下收敛等价于序列在 \(\gamma\) 生成的拓扑下收敛。也等价于在生成该拓扑的任意一族邻域基下收敛。

Theorem 1.101 连续函数是保收敛性的。即，若 \(f:X\rightarrow Y\) 连续，且 \(\lim_{n\rightarrow \infty} = a\)，则 \(\lim_{n\rightarrow \infty} f(x_n) = f(a)\)。

Proof：由 Definition 1.97 和 Definition 1.23 立即可得。

Exercise 1.102 拓扑空间 \(X\) 中的序列 \(\alpha = \{x_n: n=1,2,\dots\}\) 可视为 \(X\) 的一个子集 \(A = \{x_n: n\in \mathbb{N}^+\}\)。比较 \(A\) 的闭包点和 \(A\) 的聚点的意义。\(\alpha\) 的极限是什么？

Proof：若 \(\alpha\) 的某个子列收敛于 \(a\)，则 \(a\) 是 \(A\) 的聚点。若 \(a\) 是 \(A\) 的聚点或 \(a\in A\)，则 \(a\) 是 \(A\) 的闭包点。\(\alpha\) 的极限一定是 \(A\) 的聚点，反之不一定。

Exercise 1.103 对度量拓扑，证明 \(f: X\rightarrow Y\) 连续当且仅当 \(f(\lim x_n) = \lim f(x_n), \forall \{x_n\}\)。

Proof：若 \(\lim x_n = a\)，则

\[\forall \epsilon>0, \exists N\in \mathbb{N}^+, s.t. n>N\Rightarrow d_X(x_n, a) < \epsilon. \]

因为 \(f\) 连续，所以

\[\forall \epsilon>0, \exists \delta>0, s.t. d_X(x,a)<\delta\Rightarrow d_Y(f(x),f(a))<\epsilon. \]

即

\[\forall \epsilon>0, \exists N\in \mathbb{N}^+, s.t. n>N\Rightarrow d_Y(f(x_n),f(a))<\epsilon. \]

故 \(f(\lim x_n) = \lim f(x_n)\)。

反之，若存在 \(\{x_n\}\) 使得 \(f(\lim x_n) \neq \lim f(x_n)\)，则

\[\exists \epsilon_0>0, \{x_{n_k}\}\subset \{x_n\},s.t. \forall k, d_Y(f(x_{n_k}), f(a))>\epsilon_0. \]

但 \(\lim_{k\rightarrow \infty} d_X(x_{n_k},a)=0\)，所以 \(f\) 在 \(a\) 处不连续。

Example 1.104 对离散拓扑，什么情况下 \(x_n\rightarrow a\)？

Solution：当且仅当 \(x_n\) 从某项开始全为 \(a\)。

Example 1.105 对平凡拓扑，什么情况下 \(x_n\rightarrow a\)？

Solution：任意序列都收敛于 \(a\)。

Definition 1.106（Hausdorff 空间） 称拓扑空间 \((X,\mathcal{T})\) 是 Hausdorff 空间，当且仅当

\[\forall a,b\in X, a\neq b, \exists U,V\in \mathcal{T}, s.t. a\in U, b\in V, U\cap V = \emptyset. \]

Lemma 1.107 Hausdorff 空间中的任意有限点集都是闭集。

Proof：由 Theorem 1.68 的条件 3，只需证明所有单点集都是闭集。考虑 \(X\backslash \{x_0\}\)。对任意 \(x\neq x_0\)，存在 \(U\supset x, V\supset x_0\) 使得 \(U\cap V = \emptyset\)，即 \(x_0\notin U, U\subset X\backslash \{x_0\}\)。即 \(X\backslash \{x_0\}\) 是开集。

Exercise 1.108 是否存在拓扑空间 \(X\) 满足：\(X\) 不是 Hausdorff 空间，但所有单点集都是闭集？

Proof：考虑 \(\mathbb{R}\) 上的余有限拓扑，即定义开集为

\[\mathcal{T} = \{\emptyset,X\}\cup\{A: \#(X\backslash A)<\infty\}, \]

则任意单点集都是闭集。但因为任意两个非空开集都相交，所以任意两个点都不可分。

Definition 1.109（T1 空间） 称拓扑空间是 T1 空间如果任意有限子集都是闭集。

Theorem 1.110 设 \(X\) 是 T1 空间，\(A\subset X\)，则 \(x\) 是 \(A\) 的聚点当且仅当 \(x\) 的任意邻域都包含 \(A\) 中无穷多个点。

Proof：充分性由 Definition 1.82 直接可得。

考虑必要性。假设存在 \(x\) 的邻域 \(U\) 使得 \((A\backslash \{x\})\cap U = \{x_1,x_2,\dots,x_m\}\)，则由 Definition 1.109 可得

\[U\cap (X\backslash \{x_1,x_2,\dots,x_m\}) = U\cap (X\backslash(A\backslash \{x\})) \]

是包含 \(x\) 的开集，且它不含除 \(x\) 外其他的 \(A\) 中点。这与 \(x\) 为 \(A\) 的聚点矛盾。

Theorem 1.111 在 Hausdorff 空间中，一个点列至多收敛到一个点。

Proof：由 Definition 1.97，若一个序列收敛到 \(X\) 中不同的两个点，则与 Definition 1.106 矛盾。

1.2 连续映射

1.2.1 子空间拓扑

Lemma 1.112 考虑拓扑空间 \(X\) 的一个子集 \(A\)。设 \(\gamma_X\) 是 \(X\) 的一族邻域基，则

\[\gamma_A := \{W\cap A: W\in \gamma_X\} \]

是 \(A\) 的一族邻域基。

Proof：因为 \(\bigcup_{W\in \gamma_X} W = X\)，所以 \(\bigcup_{U\in \gamma_A}U = \bigcup_{W\in \gamma_X}(W\cap A) = (\bigcup_{W\in \gamma_X}W)\cap A = X\cap A = A\)。

对任意 \(U,V\in \gamma_A, x\in U\cap V\)，存在 \(U',V'\in \gamma_X\) 使得 \(U = U'\cap A, V = V'\cap A, W' = U'\cap V', W'\in \gamma_X\)。令 \(W := W'\cap A\) 则有 \(W\in \gamma_A\) 且 \(x\in W\subset U\cap V\)。

Definition 1.113（子空间拓扑）由 \(\gamma_A\) 生成的拓扑称为由 \(\gamma_X\) 生成的拓扑的子空间拓扑（相对拓扑）。

Lemma 1.114 设 \(A\) 为拓扑空间 \(X\) 的子集，\(\mathcal{T}_X\) 是 \(X\) 上的拓扑，则

\[\mathcal{T}_A := \{W\cap A: W\in \mathcal{T}_X\} \]

是 \(A\) 上的拓扑。

Proof：Trival，类似 1.112 直接验证。

Definition 1.115（子空间拓扑）给定拓扑空间 \((X,\mathcal{T})\) 和 \(A\subset X\)，称拓扑空间 \((A, \mathcal{T}_A)\) 是 \(X\) 的子拓扑空间，\(\mathcal{T}_A\) 是由 \(\mathcal{T}_X\) 诱导的子空间拓扑。

Theorem 1.116 设 \(\gamma_X\) 是生成 \(\mathcal{T}_X\) 的拓扑基，则由 \(\mathcal{T}_X\) 诱导的在 \(A\) 上的子空间拓扑等于由 \(\gamma_X\) 生成的 \(A\) 上的子空间拓扑（交换图）。

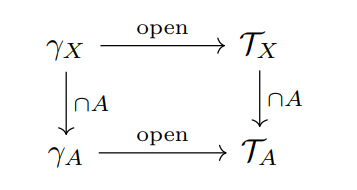
Proof：首先证明 \(U\in \mathcal{T}_A\) 在 \(\gamma_A\) 诱导的拓扑下是开集。由 Lemma 1.114，存在 \(U'\in \mathcal{T}_X\) 使得 \(U = U'\cap A\)。因为 \(\gamma_X\) 是 \(X\) 的拓扑基，所以

\[\forall y\in U', \exists B'\in \gamma_X, s.t. y\in B'\subset U'. \]

这表明

\[\forall x\in U\subset U', \exists B := (B'\cap A)\in \gamma_A, s.t. x\in B\subset U. \]

因此 \(U\) 在 \(\gamma_A\) 诱导的拓扑下是开集。

下面证明，若 \(U\) 在 \(\gamma_A\) 诱导的拓扑下是开集，则 \(U\in \mathcal{T}_A\)。即，我们要寻找 \(U'\in \mathcal{T}_X\) 使得 \(U = U'\cap A\)。因为 \(\gamma_X\) 是 \(X\) 的拓扑基，所以

\[\forall x\in U, \exists N_x\in \gamma_A, s.t. x\in N_x\subset U. \]

其中 \(N_x = N_x'\cap A, N_x'\in X\)。令 \(U' = \cup_{x\in U}N_x'\)，则由 Theorem 1.44，\(U'\) 是 \(\gamma_X\) 下的开集，即 \(U = U'\cap A\) 是 \(\gamma_A\) 下的开集。

Lemma 1.117 设 \(A\) 是 \(X\) 的子空间，\(U\) 在 \(A\) 中是开集，\(A\) 在 \(X\) 中是开集，则 \(U\) 在 \(X\) 中是开集。

Proof：因为 \(U\) 在 \(A\) 中是开集，所以由 Definition 1.115 有

\[\exists U'\in \mathcal{T}_X, s.t. U = U'\cap A. \]

又因为 \(A\in \mathcal{T}_X\)，所以 \(U = U'\cap A\in \mathcal{T}_X\)。

Lemma 1.118（子空间的闭集）设 \(A\) 是 \(X\) 的子空间，则集合 \(V\subset A\) 是 \(A\) 中闭集当且仅当它是 \(A\) 与 \(X\) 的一个闭子集的交。

Proof：假设 \(V\) 是 \(A\) 中闭集，则

\[\exists V'\subset A, s.t. V\cup V' = A, V'\in \mathcal{T}_A. \]

因为 \(A\) 是 \(X\) 的子空间，所以由 Definition 1.115 有

\[\exists U'\subset X, s.t. V' = U'\cap A, U'\in \mathcal{T}_X. \]

因此集合 \(U = X\backslash U'\) 是 \(X\) 中闭集，且

\[A\cap U = A\cap (X\backslash U') = A\backslash (X\backslash (X\backslash U')) = A\backslash U' = A\backslash (U'\cap A) = A\backslash V' = V. \]

反之，假设

\[\exists U\in X, s.t. (X\backslash U)\in \mathcal{T}_X, V = U\cap A. \]

令 \(V' := (X\backslash U)\cap A\)，则由 Definition 1.115 由 \(V'\) 是 \(A\) 中开集。又因为

\[V\cup V' = (U\cap A)\cup((X\backslash U)\cap A) = A, \]

所以 \(V\) 是 \(A\) 中闭集。

Corollary 1.119（相对闭性的传导）设 \(A\) 是 \(X\) 的子空间，\(V\) 是 \(A\) 中闭集，\(A\) 是 \(X\) 中闭集，则 \(V\) 是 \(X\) 中闭集。

Proof：由 Lemma 1.118 立即可得。

1.2.2 新映射的构造

Theorem 1.120 连续函数的复合仍为连续映射。

Proof：设有连续映射 \(f : X\rightarrow Y, g : Y\rightarrow Z\)，令 \(h = gf: X\rightarrow Z\)，则对任意开集 \(U\subset Z\)，有

\[h^{-1}(U) = (gf)^{-1}(U) = f^{-1}(g^{-1}(U)) \]

是开集。

Theorem 1.121 设 \(X\) 是拓扑空间，\(f,g: X\rightarrow \mathbb{R}\) 是连续函数。则 \(f+g,f-g,fg\) 是连续函数；当 \(g(x)\neq 0, \forall x\) 时，\(f/g\) 也是连续函数。

Proof：以加法为例。\(h: X\rightarrow \mathbb{R}^2, h(x) = (f(x), g(x))\) 是连续函数。又因为 \(+:\mathbb{R}^2\rightarrow \mathbb{R}\) 是连续函数，所以 \(f+g = +\circ h\) 连续。

Definition 1.122（含入）设 \(X\) 是拓扑空间，\(A\) 是 \(X\) 的子集，则定义含入映射 \(i_A: A\rightarrow X\) 为

\[\forall x\in A, i_A(x) = x. \]

Definition 1.123（限制）设 \(X\) 和 \(Y\) 是拓扑空间，\(A\) 是 \(X\) 的子集，称 \(f: X\rightarrow Y\) 在 \(A\) 上的限制为

\[\forall x\in A, f|_A (x) = f(x). \]

Theorem 1.124（限制区域）连续函数的限制是连续函数。

Proof：因为 \(f|_A = f\circ i_A\)，\(i_A\) 连续，所以 \(f|_A\) 连续。

Exercise 1.125 设 \(i_A: A\rightarrow X\) 是含入映射，假设 \(A\) 的拓扑满足：对任意拓扑空间 \(Y\) 和映射 \(f: Y\rightarrow A\)，\(f\) 连续当且仅当 \((i_A\circ f): Y\rightarrow X\) 连续。证明 \(A\) 的拓扑与 \(X\) 在 \(A\) 上的子空间拓扑是相同的。

Proof：设 \(U\in \mathcal{T}_A\)，则 \(f:Y\rightarrow A\) 是连续映射，当且仅当 \(i_A\circ f: Y\rightarrow X\) 是连续映射。

因此对任意映射 \(f\)，\(f^{-1}(U)\) 是 \(Y\) 中开集当且仅当 \(f^{-1}(i_A^{-1}(W)), U = W \cap A\) 是 \(Y\) 中开集。即 \(W\) 是 \(X\) 中开集。

所以 \(U\) 是 \(X\) 在 \(A\) 上的子空间拓扑的开集。

反之，若 \(U = W\cap A\)，\(W\in \mathcal{T}_X\)，则同理可知 \(U\) 是 \(A\) 中开集。

Lemma 1.126（限制值域）若 \(f:X\rightarrow Y\) 是连续函数，则 \(g_f: X\rightarrow f(X)\) 其中 \(g_f(x) = f(x), \forall x\in X\) 是连续函数。

Proof：\(f(X)\) 上的拓扑和 \(Y\) 上的拓扑相同。即 \(f(X)\) 中的开集也是 \(Y\) 中开集。

Lemma 1.127（值域延拓）若 \(f: X\rightarrow Y\) 是连续函数，\(Y\) 是 \(Z\) 的子空间，则函数 \(g: X\rightarrow Z, g(x) := f(x), \forall x\in X\) 是连续函数。

Proof：令 \(g = i_Y\circ f\) 即可。

Lemma 1.128（粘贴引理）设 \(A,B\) 是拓扑空间 \(X\) 的闭子集，\(X = A\cup B\)，且 \(f_A: A\rightarrow Y\) 和 \(f_B: B\rightarrow Y\) 是连续函数，满足

\[\forall x\in A\cap B, f_A(x) = f_B(x), \]

则函数 \(f: X\rightarrow Y\) 是连续函数

\[f(x) := \begin{cases} f_A(x), & x\in A, \\ f_B(x), & x\in B. \\ \end{cases} \]

Proof：定义 \(W = f_A(A)\cup f_B(B)\)，则对任意 \(V\subset Y\)，有

\[V = (V\cap W)\cup (V\backslash W) = (V\cap f_A(A))\cup (V\cap f_B(B))\cup (V\backslash W). \]

若 \(V\) 是 \(Y\) 中闭集，则其原像为

\[\begin{aligned} f^{-1}(V) &= f^{-1}(V\cap f_A(A))\cup f^{-1}(V\cap f_B(B)) \\ &= f_A^{-1}(V\cap f_A(A))\cup f_B^{-1}(V\cap f_B(B)) \\ &= g_A^{-1}(V\cap f_A(A))\cup g_B^{-1}(V\cap f_B(B)) \end{aligned} \]

其中，\(g_A, g_B\) 如 Lemma 1.126 定义。又因为

• \(V\) 是闭集，故 Lemma 1.118 表明 \(V\cap f_A(A)\) 和 \(V\cap f_B(B)\) 分别是 \(f_A(A)\) 和 \(f_B(B)\) 中闭集；
• 由 Lemma 1.126，\(g_A, g_B\) 连续，故 \(g_A^{-1}(V\cap f_A(A))\) 和 \(g_B^{-1}(V\cap f_B(B))\) 分别在 \(A\) 和 \(B\) 中连续；
• 由 Corollary 1.119，两个集合都是 \(X\) 中闭集。

因此闭集的原像是闭集，即 \(f\) 连续。

Exercise 1.129 证明当 \(A,B\) 非闭时，Lemma 1.128 不成立。

Proof：考虑 \(X = [0,1],A=[0,\frac 12],B=(\frac 12,1]\)，\(f_A(x) = 0, f_B(x) = 1\)，则 \(f\) 不连续。

Exercise 1.130 给出并证明开集形式的粘贴引理。

Formula：设 \(A,B\) 是拓扑空间 \(X\) 的开子集，\(X = A\cup B\)，且 \(f_A: A\rightarrow Y\) 和 \(f_B: B\rightarrow Y\) 是连续函数，满足

\[\forall x\in A\cap B, f_A(x) = f_B(x), \]

则函数 \(f: X\rightarrow Y\) 是连续函数

\[f(x) := \begin{cases} f_A(x), & x\in A, \\ f_B(x), & x\in B. \\ \end{cases} \]

Proof：开集对有限并和有限交也封闭。因此将 Lemma 1.128 中的“闭集”都改为“开集”即可。

Exercise 1.131 粘贴引理在复分析中对应的定理？

Formula：对应复解析函数的解析延拓定理。

Definition 1.132（定义域的延拓）给定 \(A\subset X\) 和函数 \(f: A\rightarrow Y\)。称函数 \(F: X\rightarrow Y\) 是 \(f\) 的延拓如果 \(F|_A = f\)。

1.2.3 同胚

Definition 1.133（同胚）称 \(f: X\rightarrow Y\) 是拓扑空间 \(X\) 与 \(Y\) 的同胚如果 \(f\) 是双射且 \(f\) 和 \(f^{-1}\) 均连续。此时称 \(X\) 和 \(Y\) 同胚或拓扑等价，记作 \(X\approx Y\)。

Lemma 1.134 若两个拓扑空间 \(X\) 和 \(Y\) 同胚，则

\[\forall a\in X, \exists b\in Y, s.t. X\backslash \{a\}\approx Y\backslash \{b\}. \]

Exercise 1.135 证明函数 \(f: \{A,B\}\rightarrow \{C\}, f(A) = f(B) = C\) 连续但不是同胚。因此同胚的一个必要条件是连通分量数相等。

Proof：\(f^{-1}\) 不存在，因此 \(f\) 不是同胚。

Example 1.136 设 \(X\) 是字母“T”形，\(Y\) 是直线段，则 \(X,Y\) 不同胚。因为删去 \(X\) 的交叉点会产生三个连通分量而删去 \(Y\) 的任意一个点都只会产生两个连通分量。

Exercise 1.138 考虑恒等映射 \(f = \text{Id}_X: (X,\mathcal{T})\rightarrow (X,\kappa)\)，\(\kappa\) 是离散拓扑，\(\mathcal{T}\) 不是。证明 \(f^{-1}\) 不连续，即 \(f\) 不是同态。

Proof：因为离散拓扑严格细于任意其他拓扑，所以存在 \(U\in \kappa\backslash \mathcal{T}\)。即 \(f^{-1}(U)\) 在 \(\mathcal{T}\) 中不是开集。因此 \(f^{-1}\) 不连续。

Exercise 1.139 给出一个 \(\mathbb{R}^2\) 中的例子证明连续双射 \(f: X\rightarrow Y\) 不一定是同胚。

Proof：令 \(X = [0,2\pi), Y = \mathbb{R}^2, f(x) = (\cos x,\sin x)\)，则 \(f\) 是连续双射，但因为 \(f^{-1}\) 不连续，所以 \(f\) 不是同胚。

Exercise 1.140 对连续函数 \(f: \mathbb{R}\rightarrow \mathbb{R}\)，定义 \(g: \mathbb{R}\rightarrow \mathbb{R}^2, g(x) = (x,f(x))\)，证明 \(g\) 是连续函数，且 \(g\) 的像（即函数的图像）与 \(\mathbb{R}\) 同胚。

Proof：因为 \(\text{Id}_\mathbb{R}\) 和 \(f\) 都是连续函数，所以 \(g = \text{Id}\times f\) 是连续函数。

取 \(g(\mathbb{R})\) 的拓扑为 \(\mathbb{R}^2\) 的子拓扑，则对任意开集 \(U\subset \mathbb{R}\)，\(f(U) = (U\times \mathbb{R})\cap g(\mathbb{R})\) 为相对开集。因此 \(g^{-1}\) 连续。即 \(g\) 是同胚。

Lemma 1.141 任意长度非零的闭区间都是同胚的。

Lemma 1.142 任意开区间（包括长度无限的区间）都是同胚的。

Lemma 1.143 开区间和闭区间不同胚。

Definition 1.144（ \(n\) 维球 \(\mathbb{S}^n\)）\(n\) 维球是 \(\mathbb{R}^{n+1}\) 的子集

\[\mathbb{S}^n := \{x\in \mathbb{R}^{n+1}: \Vert x\Vert = 1\}. \]

其北极点是 \(N = (0,0,\dots,0,1)\)。

Definition 1.145（球极投影） 球极投影 \(P: \mathbb{S}^n\backslash N\rightarrow\mathbb{R}^n\) 定义为

\[P(x) := \left(\frac {x_1}{1-x_{n+1}},\frac {x_2}{1-x_{n+1}},\dots,\frac {x_n}{1-x_{n+1}}\right). \]

Lemma 1.146 球极投影是同胚映射，其逆映射为

\[P^{-1}(y) = \frac 1{1+\Vert y\Vert^2}(2y_1,2y_2,\dots,2y_n,\Vert y\Vert^2-1). \]

Exercise 1.147 证明 2 维球和空心正方体是同胚的。

Proof：令 \(f: [-1,1]^{n+1}\rightarrow \mathbb{S}^n\) 定义为

\[f(x) = \frac{x}{\Vert x\Vert} \]

则 \(f\) 是同胚。

Theorem 1.148 同胚是拓扑空间中的等价关系。

Proof：对同胚映射 \(f: (X, \mathcal{T}_X)\rightarrow (Y, \mathcal{T}_Y)\)，可以定义 \(f_{\mathcal{T}}: \mathcal{T}_X\rightarrow \mathcal{T}_Y\)，\(f_\mathcal{T}(V) := f(V)\)，则 \(f_{\mathcal{T}}\) 是双射。因此同胚形成了拓扑空间之间的等价。

Definition 1.149（嵌入）称函数 \(f:X\rightarrow Y\) 为 \(X\) 在 \(Y\) 中的嵌入如果 \(f\) 将 \(X\) 同胚映射到 \(Y\) 的子空间 \(f(X)\)。

Example 1.150 对嵌入 \(f: [0,1]\rightarrow X\)，其像称为 \(X\) 中的弧。对 \(f: \mathbb{S}^1\rightarrow X\)，其像称为 \(X\) 中的简单闭曲线。

1.3 几类拓扑空间

1.3.1 拓扑的粗细

Definition 1.151（粗细）设 \(\mathcal{T}\) 和 \(\mathcal{T'}\) 是 \(X\) 上的两个拓扑空间。若 \(\mathcal{T}'\supset \mathcal{T}\)，则称 \(\mathcal{T'}\) 细于 \(\mathcal{T}\) 或 \(\mathcal{T}\) 粗于 \(\mathcal{T'}\)。此时也称 \(\mathcal{T}\) 和 \(\mathcal{T'}\) 是可比较的。

Lemma 1.152 设 \(\mathcal{B}\) 和 \(\mathcal{B'}\) 是 \(X\) 上的拓扑 \(\mathcal{T,T'}\) 的基，则 \(\mathcal{T'}\) 细于 \(\mathcal{T}\) 当且仅当

\[\forall x\in X, \forall B\in \mathcal{B}, \exists B'\in \mathcal{B'} s.t. x\in B'\subset B. \]

Proof：充分性：显然 \(U\in \mathcal{T}\Rightarrow U = \cup_xB'_x\in \mathcal{T'}\)。

必要性：设 \(x\in X, B\in \mathcal{B}, x\in B\)，则由 Lemma 1.31 得 \(B\) 是开集，即 \(B\in \mathcal{T}\)。

由拓扑粗细的定义得 \(B\in \mathcal{T'}\)。由 Definition 1.30 得存在 \(B'\in \mathcal{B'}\) 使得 \(x\in B'\subset B\)。

Exercise 1.153 全体非退化约当曲线的有界分量形成了一族邻域基。这族基是否细于开球形成的基？

Proof：否，这族基与开球的基是等价的。

Definition 1.154（有界补空间）\(X\) 上的有界补拓扑定义为

\[\mathcal{T} = \{U\subset X: U=\emptyset或X\backslash U有限\} \]

可数补拓扑定义为

\[\mathcal{T} = \{U\subset X: U=\emptyset或X\backslash U可数\} \]

特定点拓扑定义为

\[\mathcal{T} = \{U\subset X: U=\emptyset或p\in U\} \]

排除点拓扑定义为

\[\mathcal{T} = \{U\subset X: U=x或p\notin U\} \]

Exercise 1.155 证明上述四个空间都是拓扑。

Proof：

• 有界补拓扑：
  • 若 \(\{U_i\}\subset \mathcal{T}\)，则 \(X\backslash(\cup_iU_i) = \cap_i(X\backslash U_i)\) 有限。因此 \(\cup_iU_i\in\mathcal{T}\)。
  • 若 \(U,V\subset \mathcal{T}\)，则 \(X\backslash (U\cap V) = (X\backslash U)\cup(X\backslash V)\) 有限。因此 \(U\cap V\in \mathcal{T}\)。
• 可数补拓扑：同理。
• 特定点拓扑：
  • 若 \(\{U_i\}\subset \mathcal{T}\)，则因为 \(p\in U_i, \forall i\)，所以 \(p\in \cup_iU_i\)。
  • 若 \(U,V\subset \mathcal{T}\)，则因为 \(p\in U,p\in V\)，所以 \(p\in U\cap V\)。
• 排除点拓扑：同理。

Exercise 1.156 对三个元素的集合 \(X=\{a,b,c\}\)，列举出它的全部拓扑，重排同构的只需列举一种。

Solution：\(X\) 的拓扑有

• \(\mathcal{T_1} = \{\emptyset, \{a,b,c\}\}\)
• \(\mathcal{T_2} = \{\emptyset, \{a\}, \{a,b,c\}\}\)
• \(\mathcal{T_3} = \{\emptyset, \{a,b\},\{a,b,c\}\}\)
• \(\mathcal{T_4} = \{\emptyset,\{a\},\{b\},\{a,b\},\{a,b,c\}\}\)
• \(\mathcal{T_5} = \{\emptyset,\{a\},\{a,b\},\{a,b,c\}\}\)
• \(\mathcal{T_6} = \{\emptyset,\{a\},\{a,b\},\{a,c\},\{a,b,c\}\}\)
• \(\mathcal{T_7} = \{\emptyset,\{a\},\{b\},\{a,b\},\{a,c\},\{a,b,c\}\}\)
• \(\mathcal{T_8} = \{\emptyset,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}\)

Exercise 1.157 在 Exercise 1.156 中，哪个拓扑有异于自己的基？

Solution：拓扑 \(\mathcal{T_4,T_6,T_7,T_8}\) 都有异于自己的基。

Exercise 1.158 定义有向图 \(G = (V,E)\) 其中 \(V\) 是 Exercise 1.156 的全体拓扑，\(E\) 包含边 \(\mathcal{T_1}\rightarrow \mathcal{T_2}\) 当且仅当 \(\mathcal{T_2}\) 严格细于 \(\mathcal{T_1}\)。画出 \(G\)。

Solution：

Definition 1.159（下界拓扑）\(\mathbb{R}\) 上的下界拓扑 \(\mathcal{T}_\ell\) 是由全体形如 \([a,b), a<b\) 的半开区间生成的。在 \(\mathbb{R}\) 上赋予下界拓扑的空间记为 \(\mathbb{R}_\ell\)。

Definition 1.160（\(K\)-拓扑）\(\mathbb{R}\) 上的 \(K\)-拓扑 \(\mathcal{T}_K\) 是由全体形如 \((a,b)\) 的开区间和形如 \((a,b)\backslash K, K=\{\frac 1n: n\in \mathbb{N}\}\) 的集合形成的。在 \(\mathbb{R}\) 上赋予 \(K\)-拓扑的空间记为 \(\mathbb{R}_K\)。

Lemma 1.161 拓扑 \(\mathbb{R}_\ell\) 和 \(\mathbb{R}_K\) 都严格细于 \(\mathbb{R}\) 上的标准拓扑，但互相不可比较。

Proof：对任意 \(x\in (a,b)\)，总有 \([x,b)\in \mathcal{T}_\ell\) 和 \((a,b)\in \mathcal{T}_K\)，因此 \(\mathbb{R}_\ell\) 和 \(\mathbb{R}_K\) 都细于 \(\mathbb{R}\)。

另一方面，对任意 \(x\in \mathbb{R}\) 和邻域 \([x,b)\in \mathbb{R}_l\)，不存在标准拓扑上的开区间包含 \(x\) 且是 \([x,b)\) 的子区间；

对 \(0\in \mathbb{R}, B_K = (-1,1)\backslash K\)，不存在标准拓扑上的开区间包含 \(0\) 且是 \(B_K\) 子集的开区间。

因此 \(\mathbb{R}_l\) 和 \(\mathbb{R}_K\) 都严格细于 \(\mathbb{R}\)。

下证 \(\mathbb{R}_l\) 和 \(\mathbb{R}_K\) 不可比较。

对任意 \(x\in \mathbb{R}\) 和邻域 \([x,b)\in \mathbb{R}_l\)，不存在 \(\mathbb{R}_K\) 上的开区间包含 \(x\) 且是 \([x,b)\) 的子区间；

对 \(0\in \mathbb{R}, B_K = (-1,1)\backslash K\)，不存在半开区间包含 \(0\) 且是 \(B_K\) 子集的开区间。

Exercise 1.162 \(\mathbb{R}^2\) 上由开球生成的拓扑空间和由开正方形生成的拓扑空间是相同的。

Proof：对任意 \(x\in \mathbb{R}^2,r>0\)，均有 \([x-\frac r2,x+\frac r2]\times [x-\frac r2,x+\frac r2] \subset B(x,r)\)；

对任意 \(a,b,c,d\in \mathbb{R}\)，均有 \(B((\frac{a+b}2,\frac{c+d}2),\min\{\frac {b-a}2,\frac{d-c}2\})\subset [a,b]\times [c,d]\)。

Exercise 1.163 证明集族

\[\mathcal{C} = \{[a,b): a<b, a,b\in\mathbb{Q}\} \]

是一族拓扑基，且生成的拓扑 \(\mathcal{T}_\mathbb{Q}\) 异于下限拓扑 \(\mathcal{T}_\ell\)。

Proof：设 \(r\in \mathbb{R}\backslash \mathbb{Q}\)，则 \(r\in [r,r+1)\)。不存在 \(\mathcal{T}_\mathbb{Q}\) 中的包含 \(r\) 且包含于 \([r,r+1)\) 的半开区间。

1.3.2 序拓扑

Definition 1.164 设 \(X\) 是一族元素个数多于 1 的全序集，\(\mathcal{B}\) 是一族满足下列条件的集合：

• 所有开区间 \((a,b)\in \mathcal{B}\)；
• 设 \(a_0\) 是最小的元素（如果存在），则所有半开区间 \([a_0,b)\in \mathcal{B}\)；
• 设 \(b_0\) 是最大的元素（如果存在），则所有半开区间 \((a,b_0]\in \mathcal{B}\)。

Exercise 1.165 证明 Definition 1.164 中的 \(\mathcal{B}\) 是 \(X\) 上的拓扑基。

Proof：对任意 \(x\in X\)，若 \(x\) 是最小元 \(a_0\)，则存在 \(a_0\in [a_0,b)\in \mathcal{B}\)；若 \(x\) 是最大元 \(b_0\)，则存在 \(b_0\in (a,b_0]\in \mathcal{B}\)。否则，存在前驱元素 \(x^-<x\) 和后继元素 \(x^+>x\) 满足 \(x\in (x^-,x^+)\)。因此 \(\cup_\mathcal{B} = X\)。

对任意 \(x\in (a,b)\cap (c,d)\)，存在 \(x\in(c,\min\{b,d\})\in \mathcal{B}\)。

因此 \(\mathcal{B}\) 是 \(X\) 的拓扑基。

Example 1.166 Definition 1.37 中定义的标准拓扑就是序拓扑。

Definition 1.167（字典序）\(\mathbb{R}\times \mathbb{R}\) 上的字典序定义为

\[(a,b) < (c,d) \Leftrightarrow a<c\lor (a=c,b<d) \]

Example 1.168 字典序拓扑 \(\mathbb{R}\times \mathbb{R}\) 上的一族基为 Definition 1.164(1) 定义的所有开区间。

Example 1.169 正整数集 \(\mathbb{Z}^+\) 的序拓扑和离散拓扑是相同的。

Exercise 1.170 证明由 \(X = \{1,2\}\times \mathbb{Z}^+\) 上的字典序生成的拓扑和离散拓扑不同。

Proof：\(\{1\}\times \mathbb{Z}^+\in \kappa_X\) 不是字典序拓扑的开集。

Exercise 1.171 证明 Definition 1.164 不能推广到偏序集。

Proof：对偏序集，因为某些元素无法比较，所以无法定义开区间。

Definition 1.172 设 \(X\) 是全序集，\(a\in X\)，定义以 \(a\) 为端点的射线为

• \((a,+\infty) := \{x: x>a\}\)
• \((-\infty, a) := \{x: x<a\}\)
• \([a,+\infty) := \{x: x\geq a\}\)
• \((-\infty,a] := \{x: x\leq a\}\)

Exercise 1.173 证明开射线形成了 \(X\) 的全序拓扑的一族基。

Proof：注意到 \((a,b) = (a,+\infty)\cap (-\infty, b)\)。

Definition 1.174（有序正方形）字典序拓扑下的集合 \([0,1]\times [0,1]\) 称为有序正方形，记为 \(I_o^2\)。

1.3.3 积拓扑

Definition 1.175（积拓扑） 设 \(X\) 和 \(Y\) 是拓扑空间，则 \(X\times Y\) 上的积拓扑定义为由基

\[\overline{\gamma}_{X\times Y} := \{B_1\times B_2: B_1\in \mathcal{T}_X, B_2\in \mathcal{T}_Y\}, \]

其中 \(\mathcal{T}_X, \mathcal{T}_Y\) 分别为 \(X\) 和 \(Y\) 上的拓扑。

Exercise 1.176 证明 \(\overline{\gamma}_{X\times Y}\) 是一族拓扑基。

Proof：因为 \(X\times Y\in \overline{\gamma}_{X\times Y}\)，所以 \(\cup_{\gamma} (B_1\times B_2) = X\times Y\)。

对任意 \(B_1,B_1'\in \mathcal{T}_X\)，\(B_2,B_2'\in \mathcal{T}_Y\)，由拓扑的性质，\(B_1\cap B_1'\in \mathcal{T}_X, B_2\cap B_2'\in \mathcal{T}_Y\)。因此 \((B_1\cap B_1')\times (B_2\cap B_2')\in \overline{\gamma}_{X\times Y}\)。

所以 \(\overline{\gamma}_{X\times Y}\) 是一族拓扑基。

Exercise 1.177 给出一个 \(\overline{\gamma}_{X\times Y}\) 不是拓扑的例子。

Solution：考虑 \(\mathbb{R}\) 上的标准拓扑，则 \((0,1)^2\cup (1,2)^2\) 是 \(\overline{\gamma}_{\mathbb{R\times R}}\) 上的开集之并但不在 \(\overline{\gamma}_{\mathbb{R\times R}}\) 中。

Exercise 1.178 两个 Hausdorff 空间 \(X\times Y\) 的乘积是 Hausdorff 的。

Proof：设 \((x_1,y_1),(x_2,y_2)\in X\times Y\)，则 \(x_1\neq x_2\) 或 \(y_1\neq y_2\)，存在开集 \(U_1,U_2\subset X\) 使得 \(x_1\in U_1,x_2\in U_2,U_1\cap U_2 = \emptyset\)。取 \(U_1\times Y,U_2\times Y\in \mathcal{T}_{X\times Y}\)，则 \((U_1\times Y)\cap (U_2\times Y) = \emptyset\)。故 \(X\times Y\) 是 Hausdorff 的。

Theorem 1.179 设 \(X\) 和 \(Y\) 是拓扑空间且拓扑基分别为 \(\gamma_X\) 和 \(\gamma_Y\)，则集合

\[\gamma_{X\times Y} = \{B_1\times B_2: B_1\in \gamma_X, B_2\in \gamma_Y\} \]

是 \(X\times Y\) 的一族拓扑基。

Proof：同 1.176，trival。

Definition 1.180（投影）函数 \(\pi_1: X\times Y\) 和 \(\pi_2: X\times Y\) 定义为

\[\pi_1(x,y) = x, \pi_2(x,y) = y \]

称为 \(X\times Y\) 到它的第一个和第二个因子空间的投影。

Lemma 1.181 \(X\times Y\) 的乘积拓扑和由拓扑基

\[\mathcal{S} := \{\pi_1^{-1}(U): U\in \mathcal{T}_X\}\cup\{\pi_2^{-1}(V): V\in \mathcal{T}_Y\} \]

生成的拓扑是等价的。

Proof：令 \(\mathcal{T}\) 为 Definition 1.175 生成的拓扑，\(\mathcal{T'}\) 为 \(\mathcal{S}\) 生成的拓扑。

因为 \(\mathcal{S}\) 中的元素都属于 \(\mathcal{T}\)，所以 \(\mathcal{T'}\subset \mathcal{T}\)。

又因为对任意 \(B_1\subset X, B_2\subset Y, B_1\times B_2 = \pi_1^{-1}(B_1)\cap \pi_2^{-1}(B_2)\in \mathcal{T'}\)，所以 \(\mathcal{T}\subset \mathcal{T'}\)。

Corollary 1.182 Definition 1.180 定义的投影（相对积拓扑）是连续函数。

Proof：考虑 \(\pi_1: X\times Y\rightarrow X\)。对任意开集 \(U\in \mathcal{T}_X\)，由 Lemma 1.181 和 Definition 1.59，\(\pi_1^{-1}(U) = U\times Y\) 是 \(X\times Y\) 中开集。

Theorem 1.183（映射的乘积）给定 \(f_1: A\times X, f_2: A\times Y\)，定义 \(f: A\rightarrow X\times Y\) 为

\[f(a) := (f_1(a), f_2(a)), \]

\(f\) 是连续函数当且仅当 \(f_1\) 和 \(f_2\) 都连续。

Proof：若 \(f\) 连续，因为 \(f_1 = \pi_1\circ f, f_2 = \pi_2\circ f\)，所以 \(f_1,f_2\) 连续。

反之，需要证明若 \(U\times V\) 是开集则 \(f^{-1}(U\times V)\) 是开集。

由 Definition 1.175，\(U\times V\in \mathcal{B}_{X\times Y}\) 可推知 \(U\in \mathcal{T}_X,V\in \mathcal{T}_Y\)。

由 Definition 1.49，当且仅当 \(f(a)\in U\times V\)，即 \(f_1(a)\in U, f_2(a)\in V\)。因此有

\[f^{-1}(U\times V) = f_1^{-1}(U)\cap f_2^{-1}(V). \]

因为 \(f_1\) 和 \(f_2\) 连续，所以 \(f^{-1}(U\times V)\) 是开集。

Example 1.184 参数化曲线 \(\gamma(t) = (x(t),y(t))\) 连续当且仅当 \(x\) 和 \(y\) 连续。

1.3.4 度量拓扑

Definition 1.185（度量）称函数 \(d: X\times X\rightarrow [0,+\infty)\) 是度量，如果 \(\forall x,y,z\in X\)，

• \(d(x,y)\geq 0\)；
• \(x=y \Leftrightarrow d(x,y)=0\)；
• \(d(x,y) = d(y,x)\)；
• \(d(x,z)\leq d(x,y) + d(y,z)\)。

称 \((X,d)\) 为度量空间。

Example 1.186 设 \(X = \mathcal{C}[a,b]\) 即 \([a,b]\rightarrow \mathbb{R}\) 的全体连续函数，则

\[d(x,y) = \max_{t\in [a,b]}|x(t)-y(t)| \]

是 \(X\) 上的一个度量。

Definition 1.187（距离）称 \(d(x,y)\) 为 \(x,y\) 之间的距离。

Definition 1.188（开球）称开集

\[B_r(x) := \{y\in X: d(x,y) < r\} \]

为中心为 \(x\in X\)，半径为 \(r\) 的开球。

Lemma 1.189 若 \(d\) 是 \(X\) 上的度量，则全体开球构成了 \(X\) 的一族基。

Definition 1.190（度量拓扑）称由全体开球生成的拓扑为由 \(d\) 诱导的度量拓扑。

Lemma 1.191 集合 \(U\) 是度量拓扑中的开集当且仅当

\[\forall x\in U, \exists r>0, s.t. B_r(x)\subset U. \]

Definition 1.192（度量空间）称拓扑空间 \(X\) 可度量化，如果存在度量 \(d\) 诱导 \(X\) 上的拓扑。赋予度量的可度量化空间称为度量空间。

Definition 1.193（度量空间中的内点和内部）称 \(x\) 是集合 \(A\) 的内点如果存在开球 \(B_r(x)\) 完全包含在 \(A\) 中；\(A\) 的内点的集合称为 \(A\) 的内部，记为 \(\text{Int}(A)\)。

Definition 1.194（度量空间中的外点和外部）称 \(x\) 是集合 \(A\) 的内点如果存在开球 \(B_r(x)\) 完全包含在 \(X\backslash A\) 中；\(A\) 的外点的集合称为 \(A\) 的外部，记为 \(\text{Ext}(A)\)。

1.3.5 商拓扑

Definition 1.195（商映射）设 \(X\) 和 \(Y\) 是拓扑空间。称满射 \(q: X\rightarrow Y\) 是商映射如果 \(U\) 是 \(Y\) 中开集当且仅当 \(q^{-1}(U)\) 是 \(X\) 中开集。

Lemma 1.196 如果一个商映射是单射，则它是同态。

Proof：由定义，显然。

Exercise 1.197 设 \(f: X\rightarrow Y\) 是连续满射。证明 \(f\) 是商映射如果存在连续函数 \(s:Y\rightarrow X\) 使得 \(f\circ s = \text{Id}_Y\)。

Proof：因为 \(f\) 是连续满射，所以若 \(U\) 是 \(Y\) 中开集，则 \(f^{-1}(U)\) 是 \(X\) 中开集；若 \(f^{-1}(U)\) 是 \(X\) 中开集，则 \(s^{-1}(f^{-1}(U)) = (f\circ s)^{-1}(U) = U\) 为开集。因此 \(f\) 是商映射。

Definition 1.198（浸透）称 \(X\) 的子集 \(C\) 被满射 \(q: X\rightarrow Y\) 浸透如果 \(C\) 恰好等于 \(Y\) 的某个子集的原像，即

\[\forall y\in T, (q^{-1}(\{y\})\cap C\neq \empty)\Rightarrow (q^{-1}(\{y\})\subset C) \]

Lemma 1.199 设 \(A\subset X\) 被商映射 \(p: X\rightarrow Y\) 浸透，则对任意子集 \(U\subset X\) 有

\[p(U\cap A) = p(U)\cap p(A). \]

Proof：只需证明 \(p(U)\cap p(A)\subset p(U\cap A)\)。

假设存在 \(u\in U, a\in A, p(u) = p(a) = y\in p(U)\cap p(A)\)。因为 \(A\) 被 \(p\) 浸透，所以 \(u\in A\)，即 \(u\in A\cap U\) 且 \(y = p(u)\in p(A\cap U)\)。

Lemma 1.200 \(q\) 是商映射当且仅当 \(q\) 是连续满射且将 \(X\) 中的浸透开集映射到 \(Y\) 中开集（或将 \(X\) 中浸透闭集映射到 \(Y\) 中闭集）。

Exercise 1.201 证明 Lemma 1.200。

Proof：设 \(A\) 是 \(X\) 中浸透开集，则 \(A = q^{-1}(U), U\subset Y\)。

必要性。若 \(q\) 是商映射，则由定义 \(q\) 是连续满射。由商映射的定义知 \(U\) 是开集。

充分性。\(q\) 是连续满射。对任意 \(q^{-1}(U)\subset X\)，$ q^{-1}(U)$ 是浸透集，若 \(q^{-1}(U)\) 为开集，则由条件得 \(U\) 是开集。因此 \(q\) 是商映射。

Exercise 1.202 证明映射 \(f: \mathbb{S}^n\times I\rightarrow \mathbb{D}^{n+1}\)，\(f(x,t) = (1-t)x\) 是商映射。

Proof：对 \(\mathbb{D}^{n+1}\) 中的集合 \(U\)，若 \(f^{-1}(U)\) 是开集，即存在开集 \(V\subset \mathbb{S}^n\) 和 \((a,b)\in I\) 使得 \(f(V\times (a,b)) = U\)。

即 \(U = \{(1-t)x: x\in V, a<t<b\}\)。对任意 \(p\in U\)，\(p = (1-t)x\)，则存在 \(B(\delta, p)\) 其中 \(\delta < \sqrt{d(x,\partial U)^2 + \min\{t-a,b-t\}^2}\) 使得 \(B(\delta, p)\subset U\)。因此 \(U\) 是开集。

Definition 1.203 称映射 \(f: X\rightarrow Y\) 是开映射如果对任意开集 \(U\subset X\)，\(f(U)\) 是 \(Y\) 中开集。称 \(f\) 为闭映射如果对任意闭集 \(A\subset X\)，\(f(A)\) 是 \(Y\) 中闭集。

Example 1.204 考虑集合 \(X := [0,1]\cup [2,3], Y:=[0,2]\)，映射 \(q: X\rightarrow Y\) 定义为

\[q(x) = \begin{cases} x, & x\in [0,1]; \\ x-1, & x\in [2,3]. \end{cases} \]

是满射、连续映射和闭映射。因此 \(q\) 是商映射。但它不是开映射，因为 \([0,1]\) 是 \(X\) 中开集但其像在 \(Y\) 中不是开集。

Example 1.205 设 \(\pi_1: \mathbb{R\times R\rightarrow R}\) 是到第一个分量的投影映射，则 \(\pi_1\) 是开映射。根据 Definition 1.175，若 \(U\times V\) 是 \(\mathbb{R\times R}\) 的基中元素，则 \(\pi(U\times V)\) 是 \(\mathbb{R}\) 中开集。因此 \(\pi_1\) 将 \(\mathbb{R\times R}\) 中开集映射为 \(\mathbb{R}\) 中开集。但 \(\pi_1\) 不是 \(\mathbb{R}\) 中闭集，因为 \(C := \{(x,y): xy=1\}\) 是 \(\mathbb{R\times R}\) 中闭集但 \(\pi_1(C) = \mathbb{R}\backslash \{0\}\) 不是 \(\mathbb{R}\) 中闭集。

对 \(A:=C\cup \{0\}\)，映射 \(q_A=\pi_1|_A: A\rightarrow \mathbb{R}\) 是连续满射，但它不是开映射：集合 \(\{0\}\) 是 \(A\) 中开集且被 \(q\) 浸透，但其像 \(\{0\}\) 不是 \(\mathbb{R}\) 中开集。

Exercise 1.206 在 \(X=\mathbb{R}\) 上赋予标准拓扑，\(Y=\mathbb{Z}\) 上赋予数轴拓扑（见 Example 1.43），构造一个商映射 \(q: X\rightarrow Y\)。

Solution：令

\[q^{-1}(n) = \begin{cases} (n-\frac 12, n+\frac 12), & n为奇数 \\ [n-\frac 12, n+\frac 12], & n为偶数 \\ \end{cases} \]

则 \(q^{-1}(\{2n-1\})\) 和 \(q^{-1}(\{2n-1,2n,2n+1\})\) 是开集而 \(q^{-1}(\{2n\})\) 是闭集。故 \(q\) 为开映射。

Theorem 1.207 设 \(q: X\rightarrow Y\) 是商映射，令 \(A\) 是 \(X\) 的子空间且被 \(q\) 浸透，并定义映射 \(q_A = q|_A: A\rightarrow q(A)\)，则

• 若 \(A\) 是 \(X\) 中的闭集或开集，则 \(q_A\) 是开映射。
• 若 \(q\) 是开映射或闭映射，则 \(q_A\) 是商映射。

Proof：

• 假设 \(V\subset q(A)\)。则因为 \(A\) 被浸透，所以 \(q^{-1}(V)\subset A\)。因此 \(q_A^{-1}(V)\) 和 \(q^{-1}(V)\) 等于 \(A\) 被 \(q\) 映射为 \(V\) 的子集。即 \(V\subset q(A)\Rightarrow q_A^{-1}(V) = q^{-1}(V)\)。

• 假设 \(A\) 是开集或 \(q\) 是开映射。要证明 \(q_A: A\rightarrow q(A)\) 是商映射，只需证明对任意 \(V\subset q(A), q_A^{-1}(V)\) 是 \(A\) 中开集可推得 \(V\) 是 \(q(A)\) 中开集。

• 假设 \(A\) 是开集。因为 \(q_A^{-1}(V)\) 是 \(A\) 中开集，所以由 Lemma 1.117 得 \(q_A^{-1}(V)\) 是 \(X\) 中开集，\(q^{-1}(V)\) 是 \(X\) 中开集。又因为 \(q\) 是商映射，所以 \(V\) 是 \(Y\) 中开集。最后又 Lemma 1.114 得 \(V\) 是 \(q(A)\) 中开集。

• 假设 \(q\) 是开映射，\(q_A^{-1}(V)\) 是 \(A\) 中开集，则由 (1) 和 Lemma 1.114 有 \(q^{-1}(V) = U\cap A\)，其中 \(U\) 为 \(X\) 中开集。由 Lemma 1.51 和 \(q\) 是满射知 \(q(q^{-1}(V)) = V\)。即

  \[V = q(q^{-1}(V)) = q(U\cap A) = q(U)\cap q(A). \]

  最后一步由 Lemma 1.199 和 \(A\) 是浸透集可得。因为 \(q(U)\) 是 \(Y\) 中开集，所以 \(V\) 是 \(q(A)\) 中开集。

• \(A\) 或 \(q\) 是闭集的情形可以类似证明。

Lemma 1.208 两个商映射的复合映射是商映射。

Proof：

\[(q\circ p)^{-1}(U) = p^{-1}(q^{-1}(U)). \]

Definition 1.209（商拓扑） 设 \(q: X\rightarrow Y\) 是满射，\(X\) 是拓扑空间，\(Y\) 是集合，定义 \(U\subset Y\) 是 \(Y\) 中开集当且仅当 \(q^{-1}(U)\) 是 \(X\) 中开集，则称全体 \(Y\) 中开集为由映射 \(q\) 诱导的商拓扑。拓扑空间 \((Y,\mathcal{T}_Y)\)

\[\mathcal{T}_Y = \{U: q^{-1}(U)\in \mathcal{T}_X\} \]

称为商空间。

Exercise 1.210 证明商拓扑是拓扑。

Proof：

• \(q^{-1}(\emptyset) = \emptyset, q^{-1}(Y) = X\)，所以 \(\emptyset, Y\in \mathcal{T}_Y\)。
• 设 \(\{U_i\}\subset \mathcal{T}_Y\)，即 \(\forall i, \exists V_i\in \mathcal{T}_X, q^{-1}(U_i) = V_i\)。 因此 \(q^{-1}(\cup_iU_i) = \cup_iq^{-1}(U_i) = \cup_iV_i\in \mathcal{T}_X\)，故 \(\cup_i U_i \in \mathcal{T}_Y\)。有限交运算的封闭性类似。

Theorem 1.211 拓扑空间上定义的任意函数都诱导了一个商映射。

Proof：函数 \(f\) 诱导了 \(f(X)\) 上的商映射。

Definition 1.212（划分和自然映射） 设 \(X\) 是拓扑空间，\(X' = \{X_j: j\in J\}\) 是 \(X\) 的划分，即

\[\cup_j X_j = X: \forall j\in J, X_j\neq \emptyset; i\neq j\Leftrightarrow X_i\cap X_j=\emptyset \]

自然映射 \(\nu: X\rightarrow X'\) 定义为 \(\nu(x) := X_j\)，其中 \(X_j\) 是 \(X'\) 的唯一的包含 \(x\) 的子集。

Example 1.213 \(A\subset X\) 诱导了划分 \(X' = \{A\}\cup \{\{x\}: x\in X\backslash A\}\)。即粘合所有 \(A\) 中的点而保持其他点不变。

Example 1.214 对拓扑空间 \(X\) 上的等价关系 $\sim $，自然映射是满射 \(X\rightarrow X/ \sim\)

\[X/ \sim := \{[x]: x\in X\}, \]

其中 \([x]\) 是 \(x\) 的等价类。若 \(X/ \sim\) 上被赋予商拓扑，则自然映射成为商映射 \(x\mapsto [x]\)，\(X/ \sim\) 成为商空间。从这个角度来看，商映射也被称作粘合映射。

Example 1.215（将区间粘合为圆）在 Example 1.214 的模型下，令

\[\begin{aligned} X &= [0,1] \\ 0\sim 1;& \forall x\in \text{Int}(X), x\sim x\\ q: X\rightarrow \mathbb{S}^1;& q(t) = (\cos(2\pi t),\sin(2\pi t)). \end{aligned} \]

这个构造也可以用 Example 1.213 的模型，令 \(A = \{0,1\}\)。

Exercise 1.216 在 Example 1.214 的模型下描述下述过程

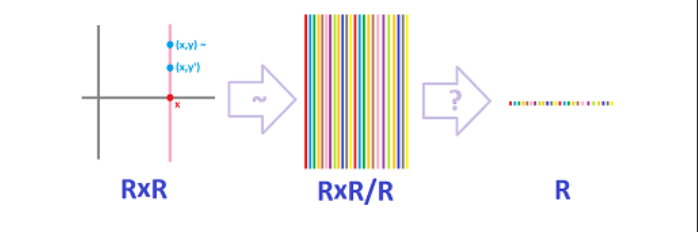
Solution：

\[\begin{aligned} X &= \mathbb{R\times R}, \\ \forall x,y,y'\in \mathbb{R} &, (x,y)\sim (x,y'), \\ q: X\rightarrow \mathbb{R} &, (x,y)\mapsto x. \end{aligned} \]

Exercise 1.217（将正方形粘合成圆柱）下图的等价类是什么？

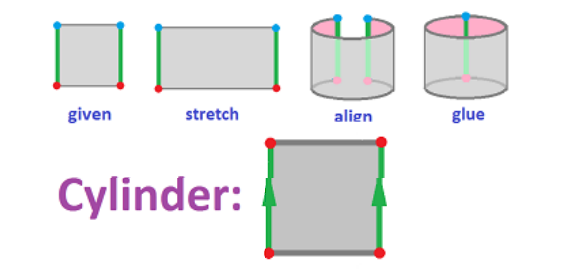
Solution：

\[\begin{aligned} X &= [0,1]^2, \\ \forall (x,y)\in \text{Int}(X) &, (x,y)\sim (x,y), \\ \forall y\in [0,1] &, (0,y)\sim (1,y). \\ \end{aligned} \]

Exercise 1.218（将正方形粘合成 Mobius 环）下图的等价类是什么？

Solution：

\[\begin{aligned} X &= [0,1]^2, \\ \forall (x,y)\in \text{Int}(X)&, (x,y)\sim (x,y), \\ \forall y\in [0,1]&, (0,y)\sim (1,1-y), \\ \end{aligned} \]

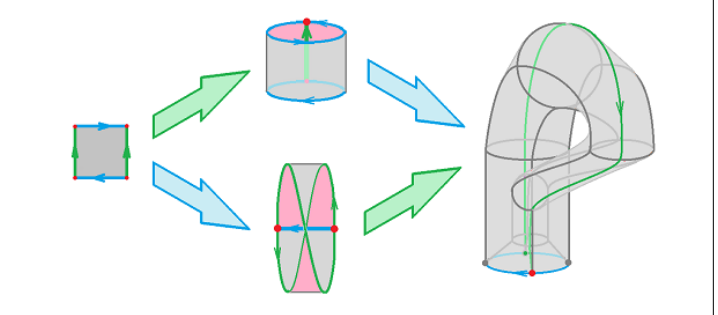
Definition 1.219（环面）环面，定义为 \(\mathbb{T}^2\)，是单位正方形按下面的等价类粘合得到的商空间

\[(x,0)\sim (x,1), (0,y)\sim (1,y) \]

Example 1.220 环面可以由柱面通过等价关系 \((x,0)\sim (x,1)\) 粘合：

Exercise 1.221 在 Definition 1.212 的定义下，对 \(X = \mathbb{T}^2\)，求对应 Definition 1.219 的等价关系的划分集 \(X'\)。

Solution：

\[X' = \{\{(x,0),(x,1)\}: 0<x<1\}\cup\{\{(0,y),(1,y)\}: 0<y<1\}\cup\{\{(x,y)\}:0<x,y<1\}\cup \{(0,0),(0,1),(1,0),(1,1)\} \]

Definition 1.222（Klein 瓶）Klein 瓶，定义为 \(\mathbb{K}^2\)，是单位正方形按下面的等价类粘合得到的商空间

\[(x,0)\sim (1-x,1), (0,y)\sim (1,y). \]

Example 1.223 Klein 瓶可以由柱面通过等价关系 \((x,0)\sim (1-x,1)\) 粘合得到。如下图所示。它不能嵌入到 \(\mathbb{R}^3\) 中：

但可以嵌入到 \(\mathbb{R}^4\) 中：

Exercise 1.224 下图的等价关系形成了什么商空间

Solution：该空间是球面 \(\mathbb{S}^2\)。

Definition 1.225（对径点）称 \(p\in \mathbb{S}^n\) 的对径点为 \(q\in \mathbb{S}^n\) 如果过 \(p\) 和 \(q\) 的直线经过球的中心。

Definition 1.226（射影平面）称如下粘合得到的商空间为射影平面

它也等价于将单位圆的对径点粘合。

Exercise 1.227 证明：可以将射影平面定义为将 \(\mathbb{R}^3\backslash 0\) 通过原点的直线上的点定义为等价类形成的商空间。

Proof：

Exercise 1.228 证明 Mobius 带可嵌入到射影平面中。

Proof：

Notation 2 对任意映射 \(h: X\rightarrow Z\)，定义 \(\ker h\) 为 \(X\) 上满足

\[x\sim x'\Leftrightarrow h(x) = h(x') \]

的等价类。\(X/\ker h\) 为对应的商空间。

Example 1.229 若 \(h\) 是群同态，则 \(\ker h\) 事实上刻画了在 \(h\) 的作用下相等的元素之间的关系。群同态的 kernel 事实上就是映射的 kernal 的一种特殊形式。

Theorem 1.230 设 \(q: X\rightarrow Y\) 是商映射。令 \(Z\) 为拓扑空间，\(h: X\rightarrow Z\) 满足在每个 \(q^{-1}(\{y\})\) 上都相等。则 \(h\) 诱导了唯一的映射 \(f: Y\rightarrow Z\) 使得 \(f\circ q = h\)。诱导映射 \(f\) 连续当且仅当 \(h\) 连续；\(f\) 是商映射当且仅当 \(h\) 是商映射。

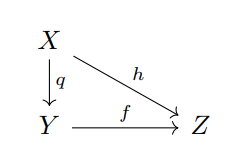
Proof：因为 \(h\) 在 \(q^{-1}(\{y\})\) 上是常数，所以 \(h(q^{-1}(\{y\}))\) 是 \(Z\) 中的单点集。令 \(f(y)\) 为这个点。

因为 \(q\) 是满射，所以 \(f: Y\rightarrow Z\) 满足

\[\forall y\in Y, \exists x\in X, s.t. q(x)=y, f(y)=h(x). \]

因为 \(f\) 的每个点值都唯一，所以 \(f\) 唯一。

若 \(f\) 连续，则复合映射 \(h = f\circ q\) 也连续。反之，设 \(h\) 连续，则对开集 \(V\subset Z\)，\(h^{-1}(V)\) 是 \(Z\) 中开集，即 \(q^{-1}(f^{-1}(V))\) 是 \(X\) 中开集。又 \(q\) 是商映射，因此 \(f^{-1}(V)\) 是 \(Y\) 中开集。

若 \(f\) 是商映射，则复合映射 \(h = f\circ q\) 是商映射。反之，设 \(h\) 是商映射，则因为 \(h\) 是满射所以 \(f\) 也是满射。若 \(f^{-1}(V)\) 是 \(Y\) 中开集，则因为 \(q\) 连续所以 \(q^{-1}(f^{-1}(V))\) 即 \(h^{-1}(V)\) 是 \(X\) 中开集，因此 \(V\) 是 \(Z\) 中开集。

Corollary 1.231 设 \(h: X\rightarrow Z\) 为连续满射，定义 \(Y := X/\ker h\) 并在 \(Y\) 上赋予商拓扑。

• 映射 \(h\) 诱导了连续双射 \(f: Y\rightarrow Z\)。进一步地，\(f\) 是同胚当且仅当 \(h\) 是商映射。
• 若 \(Z\) 是 Hausdorff 空间，则 \(Y\) 也是。

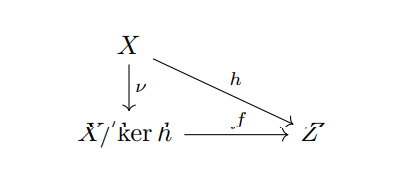
Proof：因为 \(Y\) 赋予了商拓扑，所以 \(\nu\) 是商映射。

由 Theorem 1.230，\(h\) 诱导了连续映射 \(f: Y\rightarrow Z\)，\(f([x]) = h(x)\)。因为 \(f^{-1}(h(x)) = \nu(x) = [x]\)，所以 \(f\) 是双射。

假设 \(f\) 是同胚。则 \(f\) 和 \(\nu\) 是商映射。由 Lemma 1.208，\(h\) 是商映射。反之，假设 \(h\) 是商映射，则由 Theorem 1.230 知 \(f\) 是商映射，再由 Lemma 1.196 知 \(f\) 是同胚。

假设 \(Z\) 是 Hausdorff 空间。则对 \(Y\) 中任意两个不同的点 \(y_1,y_2\)，\(f(y_1)\neq f(y_2)\) 且包含在两个不交开集中。因为 \(f\) 是双射，所以 \(f^{-1}(U)\) 和 \(f^{-1}(V)\) 也是 \(Y\) 中不交开集。

Example 1.232 定义 \(X,Z\subset \mathbb{R}^2\) 为

\[\begin{aligned} X = \{(x,n)\in \mathbb{R}^2: x\in [0,1]; n\in \mathbb{N}^+\} \\ Z = \{(x,\frac xn)\in \mathbb{R}^2: x\in [0,1]; n\in \mathbb{N}^+ \} \end{aligned} \]

则 \(X\) 是一列不交直线段之并，\(Z\) 是一列端点相同的射线之并。

设连续满射 \(h: X\rightarrow Z\) 为 \(h(x,n) = (x,\frac xn)\)，则对应的商空间为 \(X':=X/\ker h=x/B, B = \{0\}\times \mathbb{N}^+\)。

由 Corollary 1.231，映射 \(h\) 诱导了连续双射 \(f: X'\rightarrow Z\)，但 \(f\) 不是同胚。因为 \(h\) 不是商映射。

Exercise 1.233（商映射的乘积不一定是商映射）设 \(X=\mathbb{R}, X'=X/\mathbb{N}^+\)，在 \(X'\) 上赋予商拓扑，定义 \(q: X\rightarrow X'\)。令 \(\text{Id}_\mathbb{Q}: \mathbb{Q\rightarrow Q}\) 为有理数集上的恒等映射。证明

\[q\times \text{Id}_\mathbb{Q}: X\times \mathbb{Q}\rightarrow X'\times \mathbb{Q} \]

不是商映射。

Proof：

Theorem 1.234 满射 \(q: X\rightarrow Y\) 是商映射当且仅当对任意拓扑空间 \(Z\) 和函数 \(f: Y\rightarrow Z\)，\(f\) 连续等价于 \(f\circ q\) 连续。

Exercise 1.235 证明 Theorem 1.234。

Proof： \(\Rightarrow\)：设 \(Z\) 为拓扑空间，\(f: Y\rightarrow Z\)，\(f\circ q: X\rightarrow Z\) 连续，则对任意开集 \(V\subset Z\) 均有 \((f\circ q)^{-1}(V) = q^{-1}(f^{-1}(V))\subset X\) 是开集，即 \(f^{-1}(V)\subset Y\) 是开集，因此 \(q\) 连续。

\(\Leftarrow\)：令 \(Z = X\backslash \sim_q\) 即映射 \(q\) 诱导的粘合空间，\(f\) 是 \(Z\rightarrow Y\) 的诱导映射的逆，则 \(f\) 连续，因此 \(Z\) 与 \(Y\) 同胚。右 Corollary 1.231 得 \(q\) 为商映射。

1.4 连通性

Definition 1.236（分割）设 \(X\) 为拓扑空间。称一对非空开集 \(U,V\) 为 \(X\) 的分割如果 \(U\cap V=\emptyset, U\cup V=X\)。称 \(X\) 是连通的，如果不存在分割。

Exercise 1.237 为何分割要用开集定义？能否用闭集？

（个人理解）是为了和 Hausdorff 空间的定义中点对的”分离性“的定义相对应。

显然也可以用闭集定义。因为如果 \(U\cup V = X\) 则 \(U=X\backslash V\)，即 \(U,V\) 同时也是闭集。

Example 1.238 平凡拓扑是连通的。

Lemma 1.239 对 \(X\) 的一个子空间 \(Y\)，\(Y\) 的分割是一对不同的非空开集 \(A\) 和 \(B\) 使得 \(A\cup B = Y\) 且二者都不含另一个集合的极限点。

Proof：先设 \(A,B\) 是 \(Y\) 的分割，则由 Definition 1.236 得 \(A,B\) 在 \(Y\) 中都是开集。进一步知 \(A\) 也是 \(Y\) 中闭集。因此 \(\overline{A} = A, B\cap \overline{A} = \emptyset\)。

另一方面，假设 \(A\cup B = Y, A\cap \overline{B} = \emptyset, B\cap \overline{A} = \emptyset\)，则有

\[\overline{A}\cap Y = \overline{A}\cap (A\cup B) = (\overline{A}\cap A) \cup (\overline{A}\cap B) = A. \]

类似地，\(\overline{B}\cap Y = B\)。故 \(A\) 和 \(B\) 都是 \(Y\) 中闭集。即它们也都是 \(Y\) 中开集。因此形成了 \(Y\) 的分割。

Example 1.240 设 \(Y = [-1,1]\) 是 \(X = \mathbb{R}\) 的子空间。则集合 \([-1,0]\) 和 \((0,1]\) 是不交非空集，但它们不是 \(Y\) 的分割因为 \([-1,0]\) 在 \(Y\) 中不是开集。或者也可以通过 Lemma 1.239 \([-1,0]\) 含有另一个集合的极限点 \(0\) 来说明。

Example 1.241 设 \(Y = [-1,0)\cup (0,1]\)。则 \([-1,0)\) 和 \((0,1]\) 都是 \(Y\) 的非空开子集且不交，因此形成了 \(Y\) 的分割。

Example 1.242 集合 \(\mathbb{Q}\) 是不连通的，且连通子空间只有单点子集。事实上，对任意子集 \(Y\subset \mathbb{Q}\)，可选取 \(p, q\in Y, p<q\)。则任意无理数 \(a\in (p,q)\) 满足

\[Y = (Y\cap(-\infty,a))\cup(Y\cap(a,+\infty)). \]

因此 \(\mathbb{Q}\) 不连通。

Theorem 1.243 连通性在连续函数作用下是不变的。即：连通空间在连续函数的作用下的像是连通的。

Proof：设 \(X\) 是连通空间，\(f: X\rightarrow Y\) 连续。假设 \(Z = f(X)\) 不连续，则存在不交非空开集 \(U,V\) 使得 \(Z = U\cup V\)。由连续函数的定义知 \(f^{-1}(U)\) 和 \(f^{-1}(V)\) 是不交非空开集且 \(X = f^{-1}(U)\cup f^{-1}(V)\)。这与 \(X\) 连通矛盾。

Theorem 1.244（介值定理）设 \(f: X\rightarrow Y\) 是连续函数，\(X\) 是连通空间，\(Y\) 是序空间。若 \(a,b\in X\) 且 \(r\) 是 \(Y\) 中介于 \(f(a),f(b)\) 的点，则存在 \(c\in X\) 使得 \(f(c) = r\)。

Definition 1.245（道路）称拓扑空间 \(X\) 中的道路为连续函数 \(f: I\rightarrow X\)。其中 \(I := [0,1]\)，\(x_0 = f(0)\) 和 \(x_1 = f(1)\) 分别称为起点和终点。

Definition 1.246（道路连通）称拓扑空间 \(X\) 是道路连通的，如果任意两点 \(x_0,x_1\in X\) 都存在从 \(x_0\) 到 \(x_1\) 的道路。

Exercise 1.247 证明若 \([a,b]\) 是道路连通的，则 \((a,b)\) 和 \([a,b)\) 也是。

Proof：任意 \((a,b)\) 中的点之间的道路都可以不经过 \(a\) 和 \(b\)（如果经过，去掉折返部分仍为道路）。因此若 \([a,b]\) 连通，则去掉 \(a\) 和 \(b\) 后这些道路仍然保留。因此 \((a,b)\) 道路连通。\([a,b)\) 同理。

Theorem 1.248 道路连通性在连续函数作用下是不变的。即：道路连通空间在连续函数作用下的像是道路连通的。

Proof：设 \(X\) 是道路连通空间，\(f: X\rightarrow Y\) 连续。对任意 \(C,D\in Z=f(X)\)，存在原像集 \(A=f^{-1}(C),B=f^{-1}(D)\in X\)。由 \(X\) 的道路连通性知存在连续函数 \(q: [0,1]\rightarrow X\) 使得 \(q(0)=A, q(1)=B\)。由 Theorem 1.120，复合函数 \(p=fq\) 连续，\(p(0)=f(q(0))=f(A)=c, p(1)=f(q(1))=f(B)=D\)。即 \(Z\) 道路连通。

Lemma 1.249 道路连通空间是连通的。

Proof：假设拓扑空间 \(X\) 不连通但道路连通。则存在分割 \(U,V\) 满足 \(u\cap V=\emptyset,U\cup V = X\)。

考虑道路 \(f:[0,1]\rightarrow X\)。因为 \(f([0,1])\) 是连通集 \([0,1]\) 的连续像，所以 \(f([0,1])\) 连通，即它必须完全包含在 \(U\) 或 \(V\) 中。因此 \(X\) 中不存在从 \(A\) 中的点到 \(B\) 中的点的道路。这与 \(X\) 道路连通矛盾。

Exercise 1.250 连通空间不一定是道路连通的。例如空间

\[S = \{(x,\sin \frac 1x): x\in (0,1]\}. \]

（拓扑学家的曲线）是连通的因为它是 \((0,1]\) 在连续函数下的像。从而 \(\overline{S} = S\cap \{(0,y):y\in [-1,1] \}\) 也是连通的。但 \(\overline{S}\) 不是道路连通的。为什么？

Proof：考虑 \(p=(0,0),q=(1,\sin 1)\)。因为函数 \(\sin \frac 1x\) 在 \(x=0\) 处振荡间断，所以不存在定义在 \([0,1]\) 上的连续函数使得 \(f(x)|_{(0,1]} = \sin \frac 1x\)。即不存在道路。

Theorem 1.251（介值定理）数值函数 \(f\in \mathcal{C}[a,b]\) 满足

\[\forall y\in [m,M], \exists \xi\in [a,b], s.t. y=f(\xi). \]

其中 \(m=\inf_{x\in [a,b]}f(x), M=\sup_{x\in [a,b]}f(x)\)。

Exercise 1.252 通过 Theorem 1.248 导出 Theorem 1.251。

Proof：因为 \([a,b]\) 是连通空间且 \([m,M]\) 是序空间，所以由 Theorem 1.248 知介值定理成立。

Theorem 1.253（一维不动点定理）任意连续函数 \(f:[-1,1]\rightarrow [-1,1]\) 都有不动点。

Proof：若 \(f(-1)=-1\) 或 \(f(1)=1\)，则结论已经成立。否则 \(f(-1)=a>-1,f(1)=b<1\)。因此下面两个集合均非空

\[A := \{(x,f(x)): f(x)>x\}, B := \{(x,f(x)):f(x)<x\}. \]

由 Theorem 1.183 和 1.243，\(f\) 的图像

\[G := \{(x,f(x)):x\in [-1,1]\} \]

是道路连通的。

假设不存在 \(x^*\) 满足 \(f(x^*)=x^*\)，则 \(G=A\cup B\)。在拓扑空间 \(G\) 中，\(A\) 和 \(B\) 是 \(G\) 的不交相对开集。这与 \(A,B\) 道路连通矛盾。

Definition 1.255（连通分支）称连通性的等价类和道路连通性的等价类分别为连通分支和道路连通分支。

Example 1.256 拓扑学家的曲线 \(\overline{S}\) 只有一个连通分支，但有两个连通分支 \(S\) 和 \(V:=\overline{S}\backslash S\)。注意，\(S\) 是开的但不是闭的，\(V\) 是闭的但不是开的。

若将 \(V\) 中所有有理点删去，则 \(\overline{S}\) 成为只有一个连通分支但有不可数无穷多个道路连通分支的空间。

Definition 1.257（局部连通性）称空间 \(X\) 在点 \(x\) 处局部连通如果对 \(x\) 的任意邻域 \(U\) 均存在一个连通邻域 \(V\ni x,V\subset U\)。\(X\) 是局部连通的如果 \(X\) 在每个点处都局部连通。

Example 1.258 \(\mathbb{Q}\) 是不连通也不局部连通的；\([-1,0)\cup (0,1]\subset \mathbb{R}\) 是不连通但局部连通的；\(\overline{S}\) 是连通但不局部连通的；实数集上的所有区间和射线都是连通且局部连通的。

Definition 1.259（局部道路连通）称空间 \(X\) 在点 \(x\) 处局部道路连通如果对 \(x\) 的任意邻域 \(U\) 均存在一个道路连通邻域 \(V\ni x,V\subset U\)。\(X\) 是局部道路连通的如果 \(X\) 在每个点处都局部道路连通。

Theorem 1.260 拓扑空间 \(X\) 是局部连通的当且仅当对任意开集 \(U\subset X\)，\(U\) 的每个连通分支都是 \(X\) 中开集。

Theorem 1.261 拓扑空间 \(X\) 是局部道路连通的当且仅当对任意开集 \(U\subset X\)，\(U\) 的每个道路连通分支都是 \(X\) 中开集。

Theorem 1.262 拓扑空间 \(X\) 的每个道路连通分支都在它的一个连通分支中。若 \(X\) 是局部道路连通的，则它的连通分支和道路连通分支等价。

Proof：由 Lemma 1.249，道路连通分支一定连通，因此包含在连通分支中。设 \(C\) 是 \(X\) 的连通分支，\(P\) 是 \(X\) 的道路连通分支。若存在 \(x\in P,x\in C\)。已知 \(P\subset C\)。若 \(P\neq C\)，则设 \(Q\) 为 \(X\) 的全体其他包含于 \(C\) 的道路连通分支之并，则 \(C = P\cup Q\)。由 Theorem 1.261 和 \(X\) 的局部道路连通性得 \(X\) 的道路连通分支都是开集。因此 \(P\) 和 \(Q\) 是 \(X\) 的一个分割，这与 \(C\) 的连通性矛盾。

1.5 紧致性

Theorem 1.263（最值定理）连续函数可在有界闭区间上取得最大值和最小值。即若 \(f\) 在 \([a,b]\) 上连续，则存在 \(c,d\in [a,b]\) 使得

\[f(c) = \max_{x\in [a,b]}f(x), f(d) = \min_{x\in [a,b]}f(x). \]

Definition 1.264（覆盖）称拓扑空间 \(X\) 的一族子集 \(\alpha\) 是 \(X\) 的一个覆盖，如果 \(\cup_\alpha = X\)。如果 \(\alpha\) 的每个元素都是开子集，则称 \(\alpha\) 为 \(X\) 的开覆盖。

Definition 1.265（子覆盖）定义拓扑空间 \(Y\) 的子集 \(X\) 的（开）覆盖为一族满足 \(X\subset \cup_\alpha\) 的子集族。\(\alpha\) 的子覆盖为同样覆盖 \(X\) 的子集族。

Example 1.266 考虑 \(K = \{\frac 1n: n\in \mathbb{N}^+\}, X = K\cup\{0\}\)。则 \(K\) 的一个开覆盖为

\[U_n = \left(\frac 1n-\epsilon_n,\frac 1n+\epsilon_n\right), \epsilon_n = \frac 1{n(n+1)}. \]

这些开集是两两不交的。\(\mathbb{R}\) 中 \(X\) 的一个开覆盖是 \(\{U_n: n\in \mathbb{N}^+\}\cup (-\epsilon,\epsilon)\)，其中 \(\epsilon := \frac 1N\)。

Example 1.267 考虑上一例中的 \(K\) 作为 \(K\subset \mathbb{R}\) 诱导的子拓扑。每个单点集 \(s_n := \{\frac 1n\}\) 都是 \(K\) 中开集。因此 \(\{s_n: n\in \mathbb{N}^+\}\) 是 \(K\) 的一个无限开覆盖。

Exercise 1.268 考虑上一例中的 \(X\) 作为 \(X\subset \mathbb{R}\) 诱导的子拓扑。集族 \(\{\{0\}\}\cup \{s_n: n\in \mathbb{N}^+\}\) 是否为 \(X\) 的一族开覆盖？如果不是，能否找到 \(X\) 的一族两两不交的无限开覆盖？有限开覆盖呢？

Proof：不是，因为 \(\{0\}\) 不是 \(X\) 作为子拓扑的开集。

假设开覆盖 \(\alpha\) 中的某个集合 \(U\) 包含 \(0\)，则它是 \(U \supset [0,\epsilon)\cap K\)。因此 \(K\backslash U\) 只有有限个元素。即无限开覆盖不存在，只存在有限开覆盖。

Exercise 1.269 \(K\) 和 \(X\) 在开覆盖和子覆盖的本质区别是什么？

Solution：\(K\) 存在无限开覆盖，但存在 \(\alpha\) 没有有限的子覆盖；\(X\) 不存在无限开覆盖。

Definition 1.270（紧致性）称拓扑空间 \(X\) 是紧空间，如果 \(Y\) 的任意开覆盖都有有限子覆盖。

Lemma 1.271 拓扑空间 \(X\) 的子空间 \(Y\) 是紧的当且仅当 \(Y\) 的每个开覆盖都有有限子覆盖。

Lemma 1.272 若 \(X\) 是拓扑空间 \(Y\) 的紧子集，则 \(X\) 在相对拓扑下是紧空间。

Theorem 1.273（Bolzano-Weierstrass）在紧空间中，任意无限集都有聚点。

Proof：假设存在无限集 \(A\) 没有聚点，则存在 \(X\) 的开覆盖

\[\alpha = \{U_x: x\in X\} \]

使得每个 \(\alpha\) 中元素至多包含一个 \(A\) 中元素。由紧致性，\(\alpha\) 存在有限子覆盖 \(\alpha'\)。但因为有限集 \(\alpha'\) 的每个元素只包含 \(A\) 中的至多一个元素，所以 \(\alpha'\) 不覆盖 \(A\)。矛盾！

Corollary 1.274 在紧空间中，每个序列都有收敛子列。

Definition 1.275（局部紧致性）称拓扑空间在 \(x\) 点是局部紧致的，如果存在紧致子空间 \(C\subset X\) 包含 \(x\) 的一个邻域。称拓扑空间是局部紧的如果它在任意一点都是局部紧致的。

Example 1.276 实数轴 \(\mathbb{R}\) 不是紧致的，但是局部紧致的。

Theorem 1.277 拓扑空间 \(X\) 是局部紧致 Hausdorff 的，当且仅当存在紧致 Hausdorff 空间 \(Y\) 使得 \(X\) 是 \(Y\) 的子空间且 \(Y\backslash X\) 只包含一个点。

Definition 1.278（紧致化） 若 \(Y\) 是紧致 Hausdorff 空间且 \(X\) 是 \(Y\) 的真子空间，\(\overline{X} = Y\)，则称 \(Y\) 是 \(X\) 的紧致化。特别地，若 \(Y\backslash X\) 是单点集，则称 \(Y\) 是 \(X\) 的单点紧致化。

Example 1.279 在 Example 1.266 中，\(X\) 是 \(K\) 的单点紧致化。

Example 1.280 实轴 \(\mathbb{R}\) 的单点紧致化与圆周同胚。类似地，复平面的单点紧致化与球面 \(\mathbb{S}^2\) 同胚。即黎曼球 \(\mathbb{C}\cup \{\infty\}\)。

Theorem 1.281 设 \(X\) 是 Hausdorff 空间。则 \(X\) 局部紧致当且仅当给定 \(x\in X\) 及其邻域 \(U\)，存在 \(x\) 的邻域 \(V\) 使得 \(\overline{V}\) 紧致且 \(\overline{V}\subset U\)。

Corollary 1.282 设 \(X\) 是局部紧致 Hausdorff 空间且 \(A\) 是 \(X\) 的子空间。若 \(A\) 是 \(X\) 中开集或闭集，则 \(A\) 是局部紧致的。

Corollary 1.283 拓扑空间 \(X\) 与紧致 Hausdorff 空间的开子集同胚当且仅当 \(X\) 是局部紧致 Hausdorff 空间。