浅谈抽象代数

个人总结，内容或许会有大量事实错误。谨慎阅读。太菜了呃呃呃

ref:

oiwiki

x义x的博客

基本概念

与群相关的

定义

设\(G\)是非空集合，其上有二元运算\(\cdot:G\times G\to G\)，如果这二者\((G,\cdot)\)满足以下性质，则称其为一个群:

1. 结合律：对任意\(a,b,c\in G\)，都有\((a\cdot b)\cdot c=a\cdot(b\cdot c)\)。

2. 存在单位元：存在\(e\in G\)，使得对于任意\(a\in G\)，都有\(e\cdot a=a\cdot e=a\)，这里\(e\)称为\(G\)的单位元，又称为幺元。注意这里\(e\)与\(a\)之间的运算满足交换律，但整个群不一定有交换律。

3. 存在逆元：对任意\(a\in G\)，都存在相应的\(b\in G\)，使得\(a\cdot b=b\cdot a=e\)，这里，\(b\)称为\(a\)的逆元。\(a,b\)互为逆元。记\(b=a^{-1}\)。

4. 封闭性：对于任意\(a,b\in G\)，都有\(a\cdot b\in G\)。这一条其实已经隐含在二元运算中。

基本性质

对于群\((G,\cdot)\)，

1. 对于\(g_1,g_2,\dots ,g_k\in G\)，\(g_1\cdot g_2\cdot \cdots \cdot g_k\)的结果与加括号的方式无关。这就是二元运算\(\cdot\)的结合律的体现。

2. 单位元唯一，对于一个\((G,\cdot)\)，有且仅有一个\(e\)。

3. 逆唯一，对于任意一个\(a\in G\)，有且仅有一个\(b\in G\)是它的逆。

4. 消去律，对于\(a,b,c\in G\)，如果\(a\cdot c=b\cdot c\)，或者\(c\cdot a=c\cdot b\)，那么\(a=b\)。这里左右消去律都成立。

群相当常见，不损失结构的变换都自动构成群。

群的一点衍生概念

半群

对于非空集合\(G\)和其上的二元运算\(\cdot:G\times G\to G\)，若二元运算满足结合律，则称\((G,\cdot)\)是一个半群。

幺半群

若半群\((G,\cdot)\)有单位元，则称之为幺半群。

Abel 群（交换群）

对于群\((G,\cdot)\)，如果运算\(\cdot\)还满足交换律，即对于任意\(a,b\in G\)，都满足\(a\cdot b=b\cdot a\)，则称之为Abel 群，也称为交换群。

与环相关的

定义

对于非空集合\(R\)与其上的两个二元运算\(+:R\times R\to R\)和\(\cdot :R\times R\to R\)，如果\((R,+,\cdot)\)满足以下性质，则称之为环：

1. \((R,+)\)构成Abel 群，其单位元记作\(0\)，\(a\in R\)在\(+\)下的逆元记作\(-a\)。

2. \((R,\cdot)\)构成半群，即\(\cdot\)满足结合律。

3. 分配律，左右分配律都满足，对于\(a,b,c\in R\)，满足\((a+b)\cdot c=a\cdot c+b\cdot c\)，以及\(c\cdot(a+b)=c\cdot a+c\cdot b\)

为表述方便，这两个二元运算常称为该环的加法和乘法，相应的单位元称为零元和幺元。幺元不一定存在。

有些定义中要求必须存在幺元，不存在幺元的环称为伪环，注意区分。

环的一点衍生概念

幺环

存在幺元的环，其单位元记作\(1\)，称之为幺环。

交换环

对于环\((R,+,\cdot)\)，如果乘法满足交换律，则称之交换环。

除环

对于非零幺环\((R,+,\cdot)\)，如果对于任意非零元素\(a\in R\)，都存在乘法逆元，那么称之为除环。

除环中将加法单位元\(0\)视作是乘法结构中的特殊元素，因为\(0\cdot a=a\cdot 0=0\)。

发现这个式子需要推导（因为这个\(0\)是加法单位元，而不是数集中的\(0\)），于是来推一下。\(0\cdot a+0=0\cdot a=(0+0)\cdot a=0\cdot a+0\cdot a\)，第二个式子与第四个式子使用\(+\)的消去律，就得到了\(0\cdot a=0\)。另一个\(a\cdot 0=0\)是类似的。

由此我们可以发现，\(0\)不会有乘法逆元，除非它自身是乘法单位元。这样的环只有零环。零环中，\(R=\{0\}\)，\(+\)和\(\cdot\)就是一般意义下的加法和乘法。它是唯一一个只有一个元素的环，唯一一个加法单位元和乘法单位元相等的环。

这里的启示是，我们理解一般的环的乘法结构时，要去除零元的影响，考察\(R \setminus \{0\}\)。

零因子

对于\(a\in R\setminus \{0\}\)，如果存在\(b\in R\setminus\{0\}\)使得\(a\cdot b=b\cdot a=0\)，则称非零元素\(a\)为零因子。

可逆元，又称为单位

对于环\((R,+,\cdot)\)，如果\(a\in R\)存在乘法逆元，则称\(a\)为一个可逆元。

零因子不可能是可逆元，可逆元不可能是零因子。但是一个非零元素可以既不是可逆元，又不是零因子。

如果一个环没有零因子，那么就说明所有非零元素在乘法运算下封闭，即\((R\setminus \{0\},\cdot)\)构成半群。

整环

对于非零环\((R,+,\cdot)\)，如果它是交换环，有幺元，无零因子，则称它为整环。

整环具有消去律，即对于\(a,b,c\in R\)，若\(a\cdot b=a\cdot c\)，且\(a\ne 0\)，则\(b=c\)。

乘法群，又称单位群

对于幺环\((R,+,\cdot)\)，设\(R^{\times}\)为\(R\)中全体可逆元的集合，则\((R^{\times},\cdot)\)构成群，称为幺环的乘法群，或者单位群。

与域相关的

定义

域是交换除环，具体定义为：对于非空集合\(F\)以及其上的两个二元运算\(+:F\times F\to F\)和\(\cdot:F\times F\to F\)，如果它们满足以下性质，则称\((F,+,\cdot)\)是一个域：

1. \((F,+)\)构成Abel 群，其单位元记作\(0\)，\(a\in F\)在\(+\)下的逆元记作\(-a\)。

2. \((F\setminus\{0\},\cdot)\)构成Abel 群，其单位元记作\(1\)，\(a\in F\setminus \{0\}\)在\(\cdot\)下的逆元记作\(a^{-1}\)。

换言之，域是对加减乘除四则运算都封闭的代数结构。

群论的一些知识

以下无歧义时，将群\((G,\cdot)\)简称群\(G\)，\(g\cdot h\)简写为\(gh\)

子群

要理解给定群的结构，第一种方法是观察它的子结构。

对于群\((G,\cdot)\)以及\(G\)的一个子集\(H\subseteq G\)，如果\((H,\cdot)\)构成群，那么称\(H\)为\(G\)的一个子群。记作\(H\le G\)。

判定一个子集是否为子群，最简单粗暴的方式就是逐一检查是否满足群的各项定义。但是可以优化：只需判定是否对二元运算封闭，是否有单位元，是否对取逆封闭。

子群判别法：群\(G\)的子集是\(H\)，当且仅当，对任意\(g,h\in H\)，都有\(g^{-1}h\in H\)。这个的证明就验证充分性和必要性，逐一检查定义即可。

由子集生成的子群

一般地，给定\(G\)的一个子集\(S\)，\(S\)中的元素进行乘法和取逆有限次，能够得到的所有结果的集合构成\(G\)的一个子群，这称为由子集\(S\)生成的子群。

另一种表述是，在\(G\)的所有子群中，包含子集\(S\)的最小的一个子群\(H\)称为为由\(S\)生成的子群，记作\(\langle S\rangle\)。特别地，若\(S\)是单元素集\(\{x\}\)，那么\(\langle S\rangle\)又记作\(\langle x\rangle\)，称之为\(x\)的幂的循环子群。

可以证明，对于任意一个子集\(S\)，总是存在\(\langle S\rangle\)。可以用所有包含\(S\)的\(G\)的子群的交来构造。

有些子集生成的群是群\(G\)本身，这些子集称为\(G\)的生成子集。生成子集中的元素被称为生成元。一般来说，生成子集远小于群本身的规模。

循环群

定义：由单元素集生成的群称为循环群。即存在\(x\in G\)，使得\(G=\langle x\rangle\)，那么\(G\)是循环群。

可以证明，循环群的结构由它的大小唯一确定。如果循环群无限，那么它必然与整数加法群\((\mathrm Z,+)\)具有相同的结构，记作\(C_{\infty}\)或者\(\mathrm Z\)，否则设其大小为\(n\in \mathrm N_+\)，那么它必然与整数模\(n\)的同余类的加法群\((\mathrm Z/n\mathrm Z,+)\)具有相同的结构，记作\(C_n\)或者\(\mathrm Z_n\)。

这称为循环群分类定理，严格的证明需要群同构的知识。

所有的循环群都是Abel 群，而即使一个群的所有子群都是循环群，这个群也可能不是Abel 群。

阶

群的阶就是群中的元素个数，记作\(|G|\)。无限群的阶就是无限。

群内给定元素的阶就是该元素生成的循环子群的阶。即最小的正整数\(n\)使得\(x^n=e\)。如果\(n\)不存在，则记\(|x|=\infty\)

可以发现，元素的阶总是不大于群的阶。还可以证明，元素的阶总是整除群的阶。但是群的阶并非总是元素的阶的最大值，也并非是元素的阶的最小公倍数。

定理：

在有限循环群\(C_n=\langle x\rangle\)中，元素\(x^k\)的阶是

\[\dfrac{n}{\gcd(n,k)} \]

特别地，\(C_n\)的生成元的数量为\(\varphi(n)\)，这里\(\varphi(\cdot)\)是欧拉函数。

上述可以直接导出欧拉定理。

陪集

研究子群以外的元素。

给定子群，我们可以定义它的陪集：

设\(G\)是群，\(H\le G\)是\(G\)的子群，则子群\(H\)的包含\(g\)的左陪集和右陪集分别定义为集合：

\[\begin{aligned} gH=\{gh:h\in H\}\\ Hg=\{hg:h\in H\} \end{aligned} \]

陪集中的元素被称为陪集的代表元。子群本身也是其陪集。

给定群\(G\)的子群\(H\)，其所有陪集是群\(G\)的一个分划，即\(G\)是其所有陪集的不相交并。

而分划总是可以看成在某种等价关系下的等价类。对于左陪集的分划，等价关系为\(g_1\sim g_2\)当且仅当\(g_1^{-1}g_2\in H\)。对于右陪集的分划，等价关系为\(g_1\sim g_2\)当且仅当\(g_1g_2^{-1}\in H\)。这个和子群判别法有些类似。

同一子群的不同陪集的大小都相等，都等于子群的大小。由于给定子群的全体陪集构成群的一个分划，有限群的阶必定是子群的阶的整数倍。这就是Lagrange定理：

对于有限群\(G\)和它的子群\(H\le G\)，\(|G|=[G:H]|H|\)总是成立，这里\([G:H]\)表示\(H\)的左（右）陪集数，称为\(G\)中子群\(H\)的指数。

证明考虑\(h\mapsto gh\)这个映射与\(h\mapsto g^{-1}h\)互为逆映射，于是这是双射，故总是有\(|H|=|gH|\)。

由于元素的阶就是其生成的循环子群的阶，于是证明了元素的阶总是整除群的阶。

正规子群

一般情况下，给定子群的左右陪集并不相同，这也反映了给定子群的性质。

设\(N\)是\(G\)的子群，如果对于任意\(h\in N\)和\(g\in G\)，都有\(ghg^{-1}\in N\)，换言之，对任意\(g\in G\)，都有\(gNg^{-1}\subseteq N\)，则称\(N\)是\(G\)的一个正规子群。记作\(N\unlhd G\)。

这个定义中的条件等价于\(gN=Ng\)恒成立。群\(G\)总是有平凡的正规子群，即\(\langle e\rangle\)和\(G\)。

商群

对于群\(G\)和它的正规子群\(N\unlhd G\)，考虑全体陪集的集合：

\[G/N=\{gN:g\in G\} \]

可以从\(G\)上的二元运算出发，定义\(G/N\)上的二元运算\(\circ\)，使得：

\[g_1N\circ g_2N=(g_1\cdot g_2)N \]

可以证明，运算结果与代表元的选取无关。此时\((G/N,\circ)\)具有群的结构，我们称之为商群（\(G\)模\(N\)得到的商群），又称为因子群。其中的每个元素是\(G\)的一个子集，本身不是\(G\)的子集。

没有非平凡正规子群的群称为单群，它们没办法通过商群来简化。可以类比素数。

群同态

要理解给定群的结构，第二种方法是将它的结构与其他群作比较。

要比较两个群的结构，就是要构造两个群之间的映射，但是这样的映射要求必须保持群的结构，即群的运算在映射前后保持一致，这样的映射称为群的同态。

设映射\(\varphi:G\to H\)是自\((G,\cdot)\)到\((H,\odot)\)的映射，如果\(\varphi\)保持群的运算，即对于任意\(g_1,g_2\in G\)，有\(\varphi(g_1\cdot g_2)=\varphi(g_1)\odot \varphi(g_2)\)，则称映射\(\varphi\)是一个从群\(G\)到群\(H\)的同态。

群同态必然将单位元映射到单位元，将逆元映射到逆元。

关于记号：下文若不会引起歧义，将省略\(G\)和\(H\)上的二元运算的符号。但请注意二者上的二元运算是不同的。

群同构

对于一个从群\(G\)到群\(H\)的同态\(\varphi\)，我们想要知道这一同态在多大程度上反映了群\(G\)和群\(H\)的结构是一致的。

为此，我们要考察群\(G\)在同态\(\varphi\)下的像\(\varphi(G)\)。\(\varphi(G)\)是\(H\)的一个子群。若\(\varphi\)不是满射，那么\(\varphi(G)\ne H\)。若\(\varphi\)不是单射，那么\(\varphi(G)\)只反映了\(G\)的部分结构。

当\(\varphi\)是一个双射时，群\(G\)和\(H\)的结构完全一致，这种特殊的群同态称为群同构。

设\(\varphi:G\to H\)是从\(G\)到\(H\)的同态，如果\(\varphi\)是双射，则称\(\varphi\)是群\(G\)和\(H\)之间的同构，记作\(G\cong H\)。

同构的两个群的结构完全一致，如果只关心结构，那么同构的两个群完全不必区分。循环群的分类定理就是在同构意义下给出的。证明循环群的分类定理只需选取合适的映射\(\varphi\)即可。

同态的核

对于一个同态，我们想要知道有多少关于群的结构的信息在同态中损失了。

我们使用\(H\)中的单位元\(e\)在\(G\)中的原像来衡量同态中损失的结构信息。

设\(\varphi:G\to H\)是从\(G\)到\(h\)的同态，则同态\(\varphi\)的核为\(\text{ker}\varphi=\{g\in G:\varphi(g)=e\}\)，这里\(e\)是群\(H\)的单位元。

同态基本定理

同态的核\(\text{ker}\varphi\)的确精确刻画了群同态中缺失的结构信息。

我们有以下定理（同态基本定理，又称第一同构定理）：

设\(\varphi:G\to H\)是自群\(G\)到群\(H\)的同态，则\(\text{ker}\varphi\unlhd G\)，且\(G/\text{ker}\varphi\cong \varphi(G)\le H\)。

看上去有些违反直觉，不太显然，考虑证明。

首先，\(N=\text{ker}\varphi\)是群\(G\)的正规子群，因为对于任意的\(h\in N,g\in G\)都有\(\varphi(ghg^{-1})=\varphi(g)\varphi(h)\varphi(g)^{-1}=\varphi(g)\varphi(g)^{-1}=e\)，亦即\(ghg^{-1}\in \text{ker}\varphi\)。

然后，考察映射\(\Phi:G/N\to \varphi(G)\)，它满足\(\Phi(gN)=\varphi(g)\)。映射是良定义的，因为如果\(g_1N=g_2N\)，那么\(g_1^{-1}g_2\in N\)，则\(\varphi(g_1^{-1}g_2)=e\)，即\(\varphi(g_1)=\varphi(g_2)\)。映射\(\Phi\)显然是满射。

证明\(\Phi\)是单射，若\(g_1N\ne g_2N\)，则\(g_1^{-1}g_2\not\in N\)，于是\(\varphi(g_1^{-1}g_2)=\varphi(g_1)^{-1}\varphi(g_2)\ne e\)，即\(\varphi(g_1)\ne \varphi(g_2)\)，于是\(\Phi\)是单射。

故\(\Phi\)是双射，于是\(G/\text{ker}\varphi\cong \varphi(G)\)。

最后，\(\varphi(g_1)\varphi(g_2)^{-1}=\varphi(g_1g_2^{-1})\in \varphi(G)\)，由子群判别法，可知\(\varphi(G)\le H\)。

一个推论：同态\(\varphi:G\to H\)是单射，当且仅当\(\text{ker}\varphi=\{e\}\)。此时，\(G\cong \varphi(G)\le H\)。

自然同态

对于群\(G\)和其正规子群\(N\unlhd G\)，由\(\pi(g)=gN\)给出的映射\(\pi:G\to G/N\)是自\(G\)到\(G/N\)的满同态，称为自群\(G\)到商群\(G/N\)的自然同态或者自然映射。

这一结论说明，对于任何给定群的正规子群，都能够找到对应的群同态，使得这一同态的核就是给定的正规子群。

前文同态基本定理则说明，任何同态的核都是正规子群。

于是，可以说正规子群和同态的核是一体两面。

这里应有oiwiki上的交换图

群的同构定理

前文的第一同构定理

第二同构定理

先定义子集的乘积：对于群\(G\)和它的子集\(A,B\subseteq G\)，子集\(A,B\)的乘积是子集\(AB=\{ab:a\in A,b\in B\}\)。

子集的乘积并不总是子群。其根本原因是存在形如\(a\in A,b\in B\)，但\(ba\not\in AB\)的反例。

对此，有如下定理：

对于群\(G\)和它的子群\(A,B\le G\)，乘积\(AB\)是子群，当且仅当\(AB=BA\)。

证明这个就分充分性和必要性证一下，用双向包含来证等号成立即可。

而第二同构定理给出了子群乘积仍是子群的更为简单的充分条件，并且进一步确定其结构：

第三同构定理

第四同构定理

群作用

理解给定群结构的第三种方法，是考察群在集合上的作用。

定义这里的作用：

对于群\(G\)和集合\(X\)，以及映射\(f:G\times X\to X\)，记\(f((g,x))=g\cdot x\)，如果\(f\)对所有\(g_1,g_2\in G\)和\(x\in X\)都满足\(g_1\cdot(g_2\cdot x)=(g_1g_2)\cdot x\)和\(e\cdot x=x\)，那么就称该映射\(f\)为群\(G\)在集合\(X\)上的群作用。

对于满足上述定义的群作用，很自然可以如下构造：

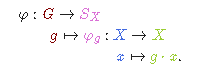
这一映射将群\(G\)中的每个元素\(g\)都对应到集合\(X\)上的一个置换\(\varphi_g\)，且置换\(\varphi_g\)将\(x\)映射到\(g\cdot x\)。

根据定义，群中单位元对应的双射\(\varphi_e\)是\(X\)上的恒等映射，而群中元素\(g\)对应的映射\(\varphi_g\)和其逆元\(g^{-1}\)对应的映射\(\varphi_{g^{-1}}\)互为逆映射。这也说明为什么\(\varphi_g\)总是双射。可以验证，\(\varphi_{g_1g_2}=\varphi_{g_1}\varphi_{g_2}\)，即\(\varphi\)是自\(G\)到\(S_X\)的群同态。

这一群同态\(\varphi\)被称为该群作用的置换表示，它将群\(G\)映射到了某个置换群上。

定义对称群：由集合\(X\)上的所有置换构成的族记作\(S\)，置换之间的复合操作记作\(\circ\),那么\((S,\circ)\)即对称群。

定义置换群：某个对称群的子群。

\(\text{ker}\varphi\)也称为该群作用的核。如果这一群同态的核是平凡的，即这个同态是单射，则称该群作用是忠实的（意指该作用的置换表示忠实地反映了群结构的信息），此时，群\(G\)与置换表示得到的置换群同构（可以使用第一同构定理）。

轨道

群作用是二元映射。固定群中的元素\(g\)，则可以得到集合上的置换\(\varphi_g\)。如果固定集合上的元素\(x\)，则可以得到群对该元素作用所有可能的结果。

定义轨道：对于群\(G\)在集合\(X\)上的作用和\(x\in X\)，称\(x\)在群\(G\)作用下的轨道是子集\(Ox=\{gx:g\in G\}\)。

容易证明，群\(G\)的作用下，集合\(X\)的全体轨道构成了该集合的一个分划，记作\(X/G\)。但是和陪集不同，这些轨道不一定等长。

稳定化子

群作用下，集合中的一个元素的轨道长度取决于有多少群里的元素对应的置换以它为不动点。

这启发以下定义：

定义稳定化子：对于群\(G\)和在集合\(X\)上的作用和\(x\in X\)，称群\(G\)中\(x\)的稳定化子是子群\(G_x=\{g\in G:gx=x\}\)。

群作用的核就是集合中所有元素的稳定化子的交。这是根据定义可以得到的。

可以观察发现，轨道\(O_x\)上的元素都和\(x\)的稳定化子的左陪集一一对应。

有一个定理：对于群\(G\)在集合\(X\)上的作用，元素\(x\in X\)的稳定化子\(G_x\)是\(G\)的子群，且子群\(G_x\)的左陪集与轨道\(O_x\)存在双射。

这是易证的。

利用Lagrange 定理（这个定理在陪集那里），可以将轨道长和稳定化子的陪集数目联系起来，这就是轨道稳定子定理。

轨道稳定子定理：对于有限群\(G\)在集合\(X\)上的作用和\(x\in X\)，有：

\[|O_x|=[G:G_x]=\dfrac{|G|}{|G_x|} \]

Burside引理

这个引理给出了群作用的轨道个数的公式。

Burnside引理：

对于群\(G\)在集合\(X\)上的作用，轨道的个数等于群中每个元素对应置换的不动点的平均个数。即：

\[|X/G|=\dfrac{1}{|G|}\sum\limits_{g\in G}|X^{g}| \]

这里，\(X^g=\{x\in X:gx=x\}\)是元素\(g\in G\)对应的不动点的集合。

考虑证明，可以算两次：

对于轨道个数进行计数，有：

\[|X/G|=\sum\limits_{o\in X/G}1=\sum\limits_{x\in X}\dfrac{1}{|O_x|}=\sum\limits_{x\in X}\dfrac{|G_x|}{|G|}=\dfrac{1}{|G|}\sum\limits_{x\in X}|G_x| \]

对于最后那坨求和\(\sum\limits_{x\in X}|G_x|\)，可以视作是集合\(\{(g,x)\in G\times X:gx=x\}\)的大小，于是自然等于\(\sum\limits_{g\in G}|X^g|\)，原式得证。

为了一碟醋包了整盘饺子。到这里我们就有了计数的手段了，去看Pólya计数