tarjan 求割点割边学习笔记

割点

对于无向图上的一个点，若把这个点去掉之后原图不连通，则为割点。割边类似。

tarjan

先考虑给这个图先打上 dfs 序，设其为 \(\operatorname{dfn}_i\)。

然后取出这颗 dfs 树（加粗的边为树边）：

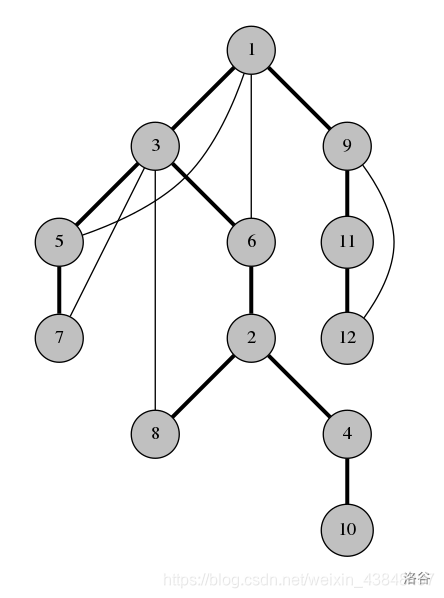
（图显然是搬的。）

考虑 \(u\) 在什么情况下为割点，显然是去掉 \(u\) 之后某一个儿子无法到达 \(fa_u\) 及以上的点了。

因为 \(u\) 的祖先的 dfs 序肯定比它小，考虑设 \(\operatorname{low}_u\) 表示 \(u\) 不经过 \(fa_u\) 能够走到的深度最小的节点。

若 \(\operatorname{low}_u\ge \operatorname{dfn}_{fa_u}\)，则证明其走不到，即 \(fa_u\) 是割点。

考虑遍历边 \((u,v)\)（\(v\not =fa_u\)），然后 \(\operatorname{low}_u\gets \operatorname{low}_v\)。

显然这样可能会有问题，比如下图的 \(\operatorname{low_4}\) 不应该是 \(1\)。

这类情况即，我们无法确定 \(v\in \operatorname{subtree}(u)\) 的 \(\operatorname{low}_v\) 是否从 \(fa_u\) 处转移。

---

于是我们考虑将 \(\operatorname{low}_u\) 定义为：\(u\) 不经过 \(fa_u\)，最多经过一条非树边能够到达的 dfs 序最小是多少。

无向图的 dfs 树有性质，非树边一定是返祖边，反证易证。

于是容易发现，\(u\) 若能够通过多条非树边到达 \(fa_u\) 以上的节点，它一定能通过一条非树边到达，所以不影响割点的判断。

然后我们考虑这样会不会出现上面的冲突。

若 \(v\in \operatorname{subtree}(u)\) 的 \(v\) 从 \(fa_u\) 转移且必须从 \(fa_u\) 转移的话，有 \(\operatorname{low}_v=fa_u\)，这类情况就算 \(u\) 转移了也不影响答案。

特殊的，对于根节点的判定是，若根节点有超过一个儿子则根节点就是割点。因为如果其儿子能联通就出现横叉边了，所以有多个儿子一定是割边。

即对于点 \(u\)，遇到树边（即 \(v\) 没有被遍历过）就 \(\operatorname{low}_u\gets \operatorname{low}_v\)，否则 \(\operatorname{low}_u\gets \operatorname{dfn}_v\)。

P3388 【模板】割点（割顶）

#include<bits/stdc++.h>
#define sd std::
// #define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define ff(i,a,b) for(int i=(a);i>=(b);i--)
#define pii sd pair<int,int>
#define X first
#define Y second
#define dbg(x) sd cout<<#x<<":"<<x<<" "
#define dg(x) sd cout<<#x<<":"<<x<<"\n"
#define inf 1e10
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=5e5+10,P=1e9+7;
int n,m;
sd vector<int> g[N];
int dfn[N],vis[N],low[N],num;
int rt;
void dfs(int u)
{
	dfn[u]=low[u]=++num;
	int son=0;
	for(auto v:g[u])
	{
		if(!dfn[v])
		{
			son++;
			dfs(v),low[u]=sd min(low[u],low[v]);
			if(low[v]>=dfn[u]&&u!=rt) vis[u]=1;
		}
		else low[u]=sd min(low[u],dfn[v]);
	}
	if(son>1&&u==rt) vis[u]=1;
}
void solve()
{
	n=read(),m=read();
	F(i,1,m)
	{
		int x=read(),y=read();
		g[x].emplace_back(y);
		g[y].emplace_back(x);
	}
	F(i,1,n) if(!dfn[i]) rt=i,dfs(i);
	int cnt=0;
	F(u,1,n) if(vis[u]) cnt++;
	put(cnt);
	F(u,1,n) if(vis[u]) printk(u);
}
int main()
{
// 	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	int T=1;
	// T=read();
	while(T--) solve();
    return 0;
}

割边

即若去掉 \((u,v)\) 这条边会导致 \(u\) 和 \(v\) 被分到了两个互不连通的连通块，这条边就是割边。

tarjan

类似的思想，考虑求出 \(\operatorname{low}_u\) 表示 \(u\) 不经过 \((u,fa_u)\) 这条边能够走到的 dfs 序最小的节点。

然后发现对于 \((u,v)\) 来讲，只要 \(v\not =fa_u\) 都可以直接转移 \(\operatorname{low}_u\gets \operatorname{low}_v\)。

U134060 【模板】割边（桥）

#include<bits/stdc++.h>
#define sd std::
// #define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define ff(i,a,b) for(int i=(a);i>=(b);i--)
#define pii sd pair<int,int>
#define X first
#define Y second
#define dbg(x) sd cout<<#x<<":"<<x<<" "
#define dg(x) sd cout<<#x<<":"<<x<<"\n"
#define inf 1e10
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=5e5+10,P=1e9+7;
int n,m;
sd vector<pii> g[N];
int dfn[N],vis[N],low[N],num;
struct node
{
	int x,y,z;
	node(int a,int b,int c)
	{
		x=a,y=b,z=c;
	}
};
sd vector<node> ans;
void dfs(int u,int fa)
{
	dfn[u]=low[u]=++num;
	for(auto [v,id]:g[u])
	{
		if(!dfn[v])
		{
			dfs(v,u),low[u]=sd min(low[u],low[v]);
			if(low[v]>dfn[u])
			{
				ans.emplace_back(node(sd min(u,v),sd max(u,v),id));
			}
		}
		else if(v!=fa) low[u]=sd min(low[u],low[v]);
	}
}
int cmp(node x,node y)
{
	return x.z<y.z;
}
void solve()
{
	n=read(),m=read();
	F(i,1,m)
	{
		int x=read(),y=read();
		g[x].emplace_back(y,i);
		g[y].emplace_back(x,i);
	}
	F(i,1,n) if(!dfn[i]) dfs(i,0);
	sd sort(ans.begin(),ans.end(),cmp);
	put(ans.size());
	for(auto [u,v,id]:ans) printk(u),put(v);
}
int main()
{
// 	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	int T=1;
	// T=read();
	while(T--) solve();
    return 0;
}