线段树优化建图学习笔记

很好理解所以写短一点。

只说区间连区间。（P6348 [PA 2011] Journeys。）

先考虑 \([a,b] \to [c,d]\) 的单向边。

建两棵线段树（动态开点）：

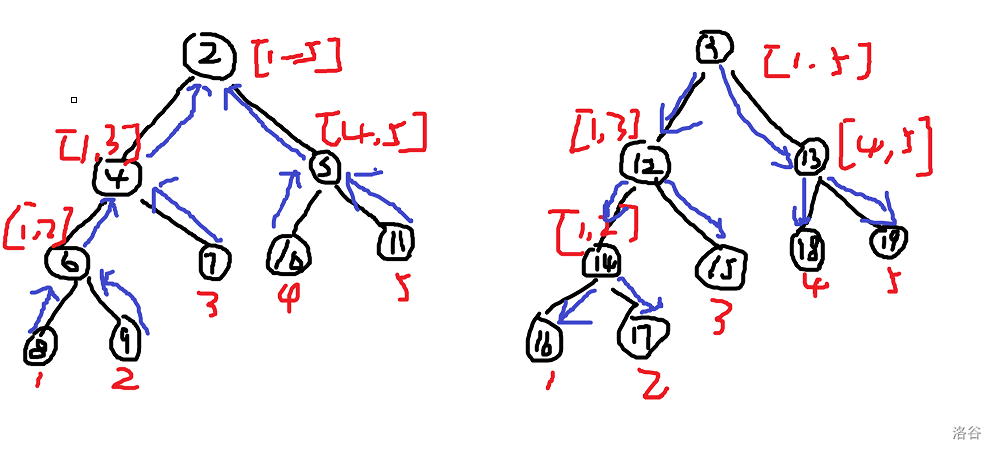
在跑最短路时就是第一棵树的叶子跑到第二棵树的叶子的最短路。

然后考虑把出树上 \([a,b]\) 分出来的 \(\log\) 个节点连向 \([c,d]\) 分出来的 \(\log\) 个节点。显然不可能暴力连。

考虑新建一个超级源点 \(st\)，\([a,b]\to st\) 以及 \(st \to [c,d]\) 就可以做到 \(2\log\) 条边，边权都是 \(0.5\)，加起来就是 \(1\) 了。

而实际上可以将边权扩大两倍，最后答案除以 \(2\)。

注意每组 \((a,b,c,d)\) 的超级源点不能一样。

但因为此时小区间访问不到大区间，所以第一棵树小区间向大区间连边，确保大区间能够走的边小区间都走。

第二棵树是大区间连向小区间，确保第一棵树走到第二棵树的大区间时能够继续走到其小区间。

但目前连的边只能做到左树到右树的一次移动，然后就只能走小区间了。

所以将左右树的叶子连边，这里连的是双向，这样可以回到左树。

双向边拆成两个单向边即可。

#include<bits/stdc++.h>
#define sd std::
//#define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define ff(i,a,b) for(int i=(a);i>=(b);i--)
#define MIN(x,y) (x<y?x:y)
#define MAX(x,y) (x>y?x:y)
#define me(x,y) memset(x,y,sizeof x)
#define pii sd pair<int,int>
#define X first
#define Y second
#define inf 1e8
#define Fr(a) for(auto it:a)
#define dbg(x) sd cout<<#x<<":"<<x<<" "
#define dg(x) sd cout<<#x<<":"<<x<<"\n"
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=5e5+10;
int n,m,P;
struct node
{
	int ls,rs;
}s1[N<<2],s2[N<<2];//s1连向s2
int pos1[N],pos2[N],tot;//pos1[i]:下标对应入树的叶子的编号
//pos2[i]:下标对应出树叶子编号
sd vector<pii> g[N*9];//2棵线段树的节点数量是八倍
void built1(int k,int l,int r)
{
	if(l==r) return pos1[l]=k,void();
	int mid=l+r>>1;
	if(!s1[k].ls) s1[k].ls=++tot;
	if(!s1[k].rs) s1[k].rs=++tot;
	built1(s1[k].ls,l,mid);
	built1(s1[k].rs,mid+1,r);
	g[s1[k].ls].emplace_back(k,0);
	g[s1[k].rs].emplace_back(k,0);
}
void built2(int k,int l,int r)
{
	if(l==r) return pos2[l]=k,void();
	int mid=l+r>>1;
	if(!s2[k].ls) s2[k].ls=++tot;
	if(!s2[k].rs) s2[k].rs=++tot;
	built2(s2[k].ls,l,mid);
	built2(s2[k].rs,mid+1,r);
	g[k].emplace_back(s2[k].ls,0);
	g[k].emplace_back(s2[k].rs,0);
}
int st,rt1,rt2;//炒鸡源点
void add1(int k,int l,int r,int x,int y)//[x,y]区间连源点
{
	if(x<=l&&y>=r)
	{
		g[k].emplace_back(st,1);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid) add1(s1[k].ls,l,mid,x,y);
	if(y>mid) add1(s1[k].rs,mid+1,r,x,y);
}
void add2(int k,int l,int r,int x,int y)//源点连[x,y]区间
{
	if(x<=l&&y>=r)
	{
		g[st].emplace_back(k,1);
		// dbg(st);
		// dg(k);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid) add2(s2[k].ls,l,mid,x,y);
	if(y>mid) add2(s2[k].rs,mid+1,r,x,y);
}
sd deque<int> q;
int dis[N*9],vis[N*9];
void dij(int s)
{
	F(i,1,tot) dis[i]=inf;
	dis[s]=0;
	q.push_front(s);
	while(!q.empty())
	{
		int u=q.front();q.pop_front();
		if(vis[u]) continue;
		vis[u]=1;
		for(auto [v,w]:g[u])
		{
			if(dis[v]>dis[u]+w)
			{
				dis[v]=dis[u]+w;
				if(w==0) q.push_front(v);
				else q.push_back(v);
			}
		}
	}
}
void solve()
{
	n=read(),m=read(),P=read();
	++tot;rt1=++tot;rt2=++tot;
	built1(rt1,1,n);
	built2(rt2,1,n);
	F(i,1,n)
	{
		g[pos1[i]].emplace_back(pos2[i],0);
		g[pos2[i]].emplace_back(pos1[i],0);
	}
	F(i,1,m)
	{
		int a=read(),b=read(),c=read(),d=read();
		st=++tot;
		add1(rt1,1,n,a,b);
		add2(rt2,1,n,c,d);
		st=++tot;
		add1(rt1,1,n,c,d);
		add2(rt2,1,n,a,b);
	}
	dij(pos1[P]);
	F(i,1,n) put(dis[pos2[i]]/2);
}
int main()
{
	int T=1;
//	T=read();
	while(T--) solve();
    return 0;
}