二次离线莫队学习笔记

之前想学好久的，去年咋都不会，现在终于会了。

作者不是很会分析复杂度哈，默认 \(n,m\) 同阶。

引入

考虑一个问题的莫队解法：

给你一个长为 \(n\) 的序列 \(a\)，\(m\) 次询问，每次查询一个区间的逆序对数。\(n,m\le 10^5\)。\(a_i\le 10^9\)。

显然，普通莫队每次在线段树内改的复杂度是 \(O(n\sqrt n \log n)\) 的，无法接受，考虑优化。

优化

考虑端点移动的贡献，假设现在区间为 \([l,r]\)，要右移到 \([l,r+1]\)，贡献显然是 \([1,r]\) 中比 \(a_{r+1}\) 大的数量，减去 \([1,l-1]\) 中比 \(a_{r+1}\) 大的数量。

前者可以 \(O(\log)\) 预处理掉，而后者是一个二维数点，考虑扫描线。考虑把所有莫队中要移动的端点 \((l,r)\) 都塞进去。这样的对一共有 \(O(n\sqrt m)\) 个。这些询问可以看作矩阵，而 \((i,a_i)\) 是一个点，一共 \(O(n)\) 个点。横坐标 \(i\)，纵坐标 \(a_i\)，大概就是这样（红色阴影部分是一个询问）：

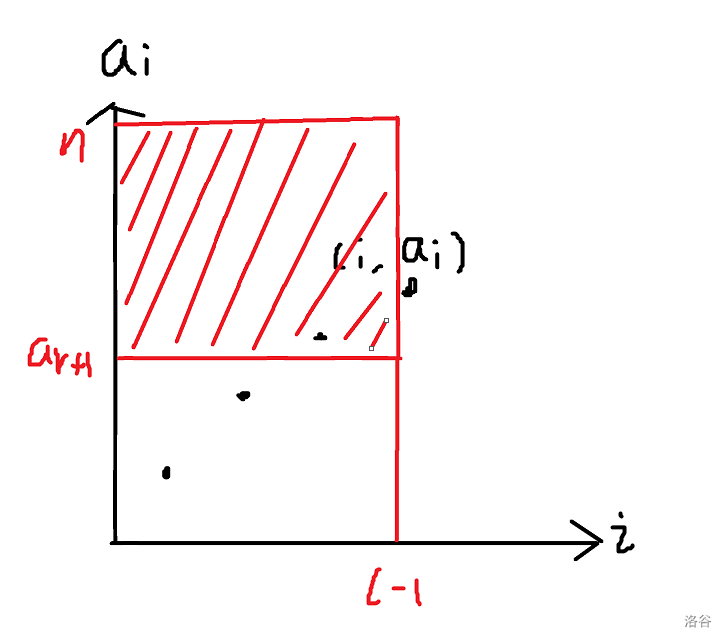
假设插入的复杂度是 \(O(A)\)，询问的复杂度是 \(O(B)\)，则总复杂度为 \(O(An\sqrt m +Bn)\)，可以值域分块将复杂度平衡成 \(A=O(1),B=O(\sqrt V)\)。而这个 \(V\) 是可以通过离散化优化成 \(O(n)\) 数量级的。

具体的：对 \(y\) 坐标进行分块，分块维护每个块的和、后缀和（因为要 \(O(1)\) 查 \(sum(a_{r+1},n)\)。）

• 对于询问，查后缀和即可。
• 对于修改，只改了 \(a_{i}\) 那个地方的值，\(O(\sqrt V)\) 暴力处理一下后缀和的改变即可。

时间复杂度 \(O(n\sqrt m+n\sqrt n)\)。

但这样空间是 \(O(n\sqrt m)\) 的，可能爆炸。因为莫队每一次移动端点一定是一个端点不动，另一个端点连续的动一个区间，记录这个区间即可。而每次询问只会记录 \(2\) 个区间，空间是 \(O(m)\) 的。

当然，处理的时候是逐一处理的。排序的时候，因为 \(l\) 是固定的，对 \(l\) 排序即可。

\(r\) 收缩处理类似，但是 \(l\) 伸缩是反着来的，再反着来一遍即可。