主席树学习笔记
前置知识
线段树,包括权值线段树、动态开点等。
前言
主席树,即可持久化线段树。
可持久化:可以保留每一个历史版本,并且支持操作的不可变特性。(来自oiwiki。)
实现
考虑如何记录历史信息。
例题(P3919 【模板】可持久化线段树 1(可持久化数组)):
维护一个数组,支持在某个历史版本修改以及访问某个历史版本上某个位置的值。
考虑线段树的处理过程,每次单修最多改变线段树上 \(\log n\) 个结点的值,于是考虑将这改变的 \(\log n\) 个结点重新建出来变成新版本。
借用一个 oiwiki 的图:
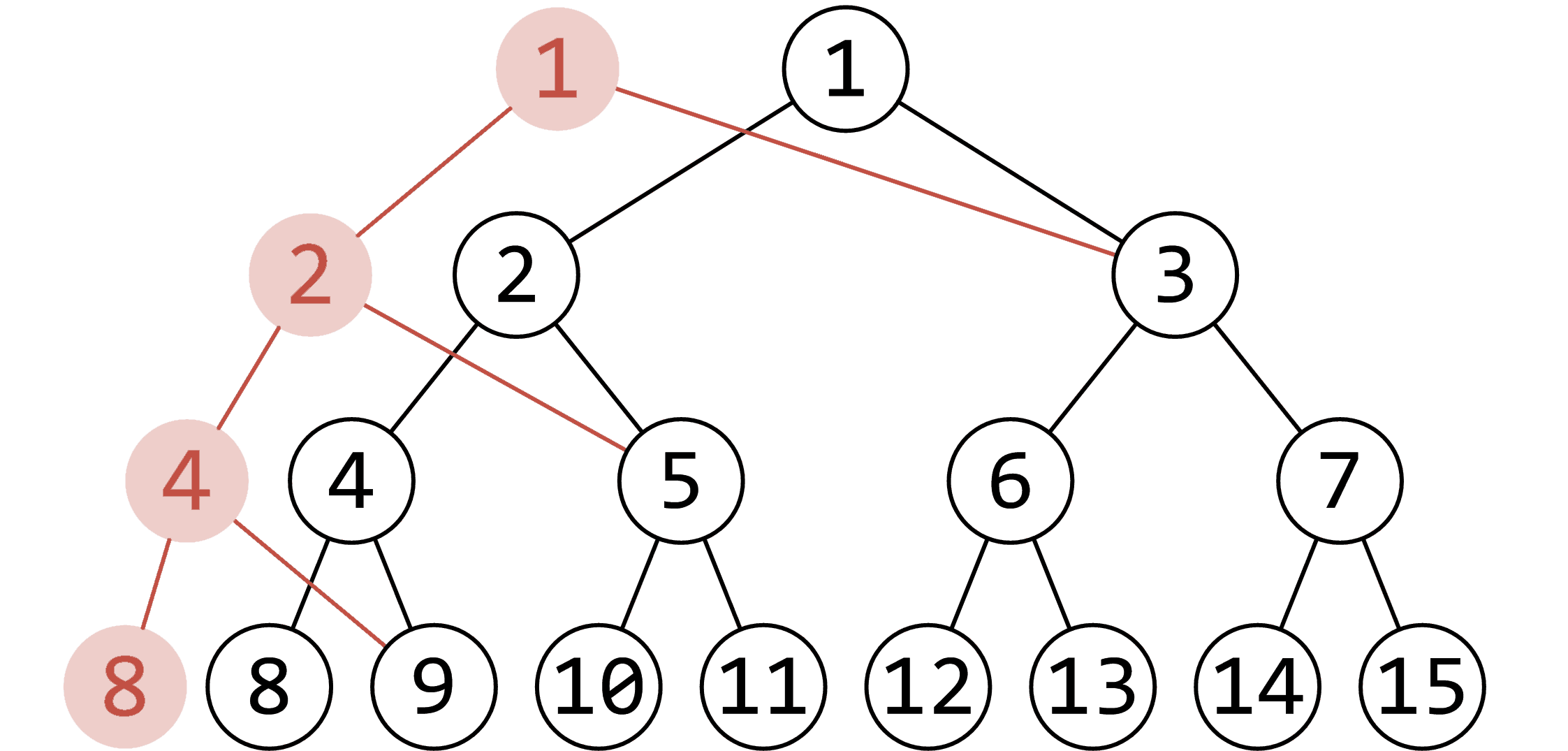
\(m\) 次修改,每次最多增加 \(\log\) 个节点,空间是可接受的。
主席树的特点:
- 有很多根。每一个根对应一个完整的线段树。
- 每个节点不止一个父节点。
- 增加的非叶子节点一个连向其他版本节点,一个连向新节点。
- 需要动态开点。
定义
需要记录:左儿子、右儿子、权值。
struct node
{
int ls,rs,val;
}s[N];
新建节点
int mknode(int x)
{
s[++cnt]=s[x];
return cnt;
}
建树
这道题没有维护区间信息,不需要 pushup。
int built(int k,int l,int r)
{
k=++cnt;
if(l==r)
{
s[k].val=a[l];
return cnt;
}
int mid=l+r>>1;
s[k].ls=built(s[k].ls,l,mid);
s[k].rs=built(s[k].rs,mid+1,r);
return k;
}
修改
int update(int k,int l,int r,int x,int v)
{
k=mknode(k);
if(l==r)
{
s[k].val=v;
return k;
}
int mid=l+r>>1;
if(x<=mid) s[k].ls=update(s[k].ls,l,mid);
else s[k].rs=update(s[k].rs,mid+1,r);
return k;
}
询问
int ask(int k,int l,int r,int x)
{
if(l==r) return s[k].val;
int mid=l+r>>1;
if(x<=mid) return ask(s[k].ls,l,mid,x);
else return ask(s[k].rs,mid+1,r,x);
}
存根
int main()
{
n=read(),m=read();
F(i,1,n) a[i]=read();
rt[0]=mknode(0,1,n);//rt[i] 为 i 版本的根编号,刚开始编号为 0
F(i,1,m)
{
int root=read(),op=read(),x=read();
if(op==1)
{
int y=read();
rt[i]=update(rt[root],1,n,x,y);
}
else
{
put(ask(rt[root],1,n,x));
rt[i]=rt[root];
}
}
}
完整代码
#include<bits/stdc++.h>
#define sd std::
//#define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define ff(i,a,b) for(int i=(a);i>=(b);i--)
#define MIN(x,y) (x<y?x:y)
#define MAX(x,y) (x>y?x:y)
#define me(x,y) memset(x,y,sizeof x)
#define pii sd pair<int,int>
#define X first
#define Y second
#define Fr(a) for(auto it:a)
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=1e6+10;
int a[N],rt[N],cnt;
struct node
{
int ls,rs,val;
}s[N<<5];
int mknode(int x)
{
s[++cnt]=s[x];
return cnt;
}
int built(int k,int l,int r)
{
k=++cnt;
if(l==r)
{
s[k].val=a[l];
return cnt;
}
int mid=l+r>>1;
s[k].ls=built(s[k].ls,l,mid);
s[k].rs=built(s[k].rs,mid+1,r);
return k;
}
int update(int k,int l,int r,int x,int v)
{
k=mknode(k);
if(l==r)
{
s[k].val=v;
return k;
}
int mid=l+r>>1;
if(x<=mid) s[k].ls=update(s[k].ls,l,mid,x,v);
else s[k].rs=update(s[k].rs,mid+1,r,x,v);
return k;
}
int ask(int k,int l,int r,int x)
{
if(l==r) return s[k].val;
int mid=l+r>>1;
if(x<=mid) return ask(s[k].ls,l,mid,x);
else return ask(s[k].rs,mid+1,r,x);
}
int n,m;
int main()
{
n=read(),m=read();
F(i,1,n) a[i]=read();
rt[0]=built(0,1,n);//rt[i] 为 i 版本的根编号,刚开始编号为 0
F(i,1,m)
{
int root=read(),op=read(),x=read();
if(op==1)
{
int y=read();
rt[i]=update(rt[root],1,n,x,y);
}
else
{
put(ask(rt[root],1,n,x));
rt[i]=rt[root];
}
}
}
例题
SPOJ TTM To the moon
trick:标记永久化。
因为如果下传标记,就无法保证每次改的节点数只有 \(O(\log)\) 层。
于是考虑每次只是打一个标记而不下传,修改/查询的时候累计一下标记即可。
先阐述 tag 的含义:即线段树上某节点的子树都要加 tag,且这个节点的 val 已经加上了 tag 的值。
本题实现过程
- 修改:
设区间 \((l,r)\) 加 \(v\)。

假设将 \((l,r)\) 分成了如上区间(A 和 B),A 和 B 是递归的最后一层,也是打 tag 的两个节点。
区间加,即线段树上这个区间子树内的都要加,而 A 和 B 上层的节点也要加但没打 tag,所以此时直接将区间的权值加上对应值即可。
k=++cnt;
s[k]=s[pre];
s[k].val=s[pre].val+(MIN(y,r)-MAX(x,l)+1)*val;
若为底层节点(AB),则在此之后还要打 tag。
if(x<=l&&y>=r) return s[k].tag+=val,void();
- 查询
多传一个参代表累计的 tag 的值,注意递归底层不加 tag 的值,因为定义中说这个节点的 val 已经加上自身 tag 了。
int ask(int k,int l,int r,int x,int y,int sum)//sum为标记之和
{
if(x<=l&&y>=r) return s[k].val+(r-l+1)*sum;
int mid=l+r>>1,res=0;
if(x<=mid) res+=ask(s[k].ls,l,mid,x,y,sum+s[k].tag);
if(y>mid) res+=ask(s[k].rs,mid+1,r,x,y,sum+s[k].tag);
return res;
}
完整代码:
#include<bits/stdc++.h>
#define sd std::
#define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define ff(i,a,b) for(int i=(a);i>=(b);i--)
#define MIN(x,y) (x<y?x:y)
#define MAX(x,y) (x>y?x:y)
#define me(x,y) memset(x,y,sizeof x)
#define pii sd pair<int,int>
#define X first
#define Y second
#define Fr(a) for(auto it:a)
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=2e5+10;
int n,m,cnt,rt[N],a[N];
struct node
{
int ls,rs,val,tag;
}s[N<<5];
void built(int &k,int l,int r)
{
k=++cnt;
s[k].tag=s[k].ls=s[k].rs=0;
if(l==r)
{
s[k].val=a[l];
return;
}
int mid=l+r>>1;
built(s[k].ls,l,mid),built(s[k].rs,mid+1,r);
s[k].val=s[s[k].ls].val+s[s[k].rs].val;
}
void update(int &k,int pre,int l,int r,int x,int y,int val)
{
k=++cnt;
s[k]=s[pre];
s[k].val=s[pre].val+(MIN(y,r)-MAX(x,l)+1)*val;
if(x<=l&&y>=r) return s[k].tag+=val,void();
int mid=l+r>>1;
if(x<=mid) update(s[k].ls,s[pre].ls,l,mid,x,y,val);
if(y>mid) update(s[k].rs,s[pre].rs,mid+1,r,x,y,val);
}
int ask(int k,int l,int r,int x,int y,int sum)//sum为标记之和
{
if(x<=l&&y>=r) return s[k].val+(r-l+1)*sum;
int mid=l+r>>1,res=0;
if(x<=mid) res+=ask(s[k].ls,l,mid,x,y,sum+s[k].tag);
if(y>mid) res+=ask(s[k].rs,mid+1,r,x,y,sum+s[k].tag);
return res;
}
void solve()
{
n=read(),m=read();
F(i,1,n) a[i]=read();
built(rt[0],1,n);
int now=0;
F(i,1,m)
{
char op[2];
int l,r,d;
scanf("%s",op);
if(op[0]=='Q')
{
l=read(),r=read();
put(ask(rt[now],1,n,l,r,0));
}
if(op[0]=='C')
{
l=read(),r=read(),d=read();
now++;
update(rt[now],rt[now-1],1,n,l,r,d);
}
if(op[0]=='H')
{
l=read(),r=read(),d=read();
put(ask(rt[d],1,n,l,r,0));
}
if(op[0]=='B') now=read();
}
}
signed main()
{
int T=1;
// T=read();
while(T--) solve();
return 0;
}
注意:标记永久化时若有多个标记必须满足交换律,否则无法确定合并顺序。
参考资料
代码实现参考 oiwiki。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号