Burnside引理和Polya定理学习笔记
搬的ljw的,这下这下了。
通常用来解决涉及本质不同的计数问题。
群
定义
若集合 \(G \neq \emptyset\),且 \(G\) 上的某个运算 \(\cdot\) 构成的代数结构 \((G,\cdot)\) 满足以下性质:
- 封闭性:\(\forall a,b \in G,a \cdot b \in G\)。
- 结合律:\(\forall a,b,c \in G,(a \cdot b) \cdot c=a \cdot (b \cdot c)\)。
- 单位元:\(\exists e \in G,\forall \in G,a \cdot e =a\)。
- 逆元:\(\forall a \in G,\exists b \in G,a \cdot b=e\)。称 \(b\) 为 \(a\) 的逆元,记作 \(a^{-1}\)。
则 \(G\) 是一个群。
对称群
易证,集合 \(G\) 上的所有置换关于置换的乘法满足封闭性、结合律、有单位元 \((\)每个元素映射成它自己\()\)、有逆元 \((\)交换置换表示中的上下两行\()\),因此构成一个群。对称群就是给定集合上的全体置换的集合。
置换群:对称群的子群,即一些 \((\)未必是全体\()\) 置换构成的群。
性质
- 一个群中的单位元唯一。
- 一个群中 \(x\) 的逆元唯一。
子群
定义
对于群 \((G,\cdot)\) 的一个子集 \(S\),如果 \((S,\cdot)\) 也是一个群,则称 \(S\) 是 \(G\) 的一个子群,记作 \(S \leq G\)。
要判定 \(S \subseteq G\) 是不是子群,只需要判定它对二元运算封闭、有单位元且对取逆封闭就好了,因为结合律自然成立。
生成子群
一般的,给定群 \(G\) 中的一个子集 \(S\),从 \(S\) 中的元素出发,重复进行乘法和取逆操作,能够得到的所有结果成为 \(G\) 的一个子群,这称为集合 \(S\) 的生成子群。
而对于群 \(G\) 中的一个子集 \(S\),若 \(G\) 的一个子群 \(H\) 是包含 \(S\) 的最小的群,则称 \(H\) 为 \(S\) 的生成子群,并记作 \(\left \langle S \right \rangle\)。特别的,如果 \(S=\{x \}\) 是单元素集合,则 \(\left \langle S \right \rangle\) 也记作 \(\left \langle x \right \rangle\),称为 \(x\) 的循环子群。有些子集生成的子群是群本身,这样的子集尤为特殊,称为群的生成子集,这些子集中的元素被称为生成元。
循环群
仅由一个元素生成的群的结构非常简单,这样的群称为循环群。
可以证明,循环群的结构由其大小唯一确定。如果循环群无限,则它必然和整数的加法群 \((Z,+)\) 具有相同的群结构,记作 \(C_{\infty}\)。否则,设群元素的个数为 \(n \in N_+\),记作 \(C_n\)。
陪集
对于群 \((G,\cdot)\) 的一个子群 \(H\):
- 如果 \(H \leq G\),对于 \(a \in G\),定义 \(H\) 的一个左陪集为 \(_{a}H=\{a \cdot h|h \in H \}\)。
- 如果 \(H \leq G\),对于 \(a \in G\),定义 \(H\) 的一个右陪集为 \(H_a=\{h \cdot a|h \in H \}\)。
注意陪集不一定是一个群,因为陪集显然可能没有单位元。
性质
下面只讨论右陪集,左陪集同理。
性质 \(1\):
如果 \(h_1 \neq h_2 \in H\),那么 \(h_1 \cdot a \neq h_2 \cdot a\)。
性质 \(2\):
因为 \(H\) 是一个群,所以 \(e \in H\),所以 \(e \cdot a=a \in H_a\)。
性质 \(3\):
从左往右推:根据性质 \(2\),我们有 \(a \in H_a\),所以 \(a \in H\)。
从右往左推:由于群的封闭性,当 \(a \in H\) 时,必然有 \(H_a=H\)。
性质 \(4\):
从左往右推:根据性质 \(2\),我们有 \(a \in H_a\),所以 \(a \in H_b\)。所以 \(h \cdot b=a\),其中 \(h \in H\) 且是一个未知元素,故 \(a \cdot b^{-1} =h \in G\)。
从右往左推:根据性质 \(3\),我们有 \(H_{a \cdot b^{-1}} =H\),所以 \(H_a=H_b\)。
性质 \(5\):
意思是 \(H\) 的任意两个陪集要么相等,要么没有交集。
考虑反证法。设 \(c \in H_a \cap H_b\),那么 \(\exists h_1,h_2 \in H,h_1 \cdot a=h_2 \cdot b=c\)。那么 \(a \cdot b^{-1}=h_1^{-1} \cdot h_2 \in H\),根据性质 \(4\) 有 \(H_a=H_b\),与假设不符。
拉格朗日定理
设 \(H\) 是有限群 \(G\) 的一个子群,则 \(|H|\) 整除 \(|G|\)。即:
其中 \([G:H]\) 表示 \(G\) 中 \(H\) 不同的陪集数。
证明
根据陪集的性质 \(1\) 和 性质 \(5\),\(H\) 的所有陪集大小相等且互不相交,所以 \(G\) 可以划分成若干个互不相交的陪集的并集。
群在集合上的作用
定义
设一个群 \((G,\cdot)\) 和集合 \(X\),如果满足 \(\forall g \in G,x \in X,y=g \cdot x \in X\) \((\)封闭性\()\),且:
- \(e \cdot x=x\)。\((\)单位元\()\)
- \((g_1 \cdot g_2)(x)=g_1 \cdot(g_2 \cdot (x))\)。\((\)交换律\()\)
则称 \(G\) 为集合 \(X\) 上的作用。如果我们固定 \(g\),就能得到元素 \(g\) 在集合 \(X\) 上的作用。
第一个条件表示单位元作用在 \(X\) 的某一个元素 \(x\) 上是恒等作用。第二个条件表示两个元素进行运算 \(\cdot\) 的作用效果就等于两个元素先后作用的效果。
例子
\(G\) 是六阶对称群的子群。显然这是满足条件一和条件二的。
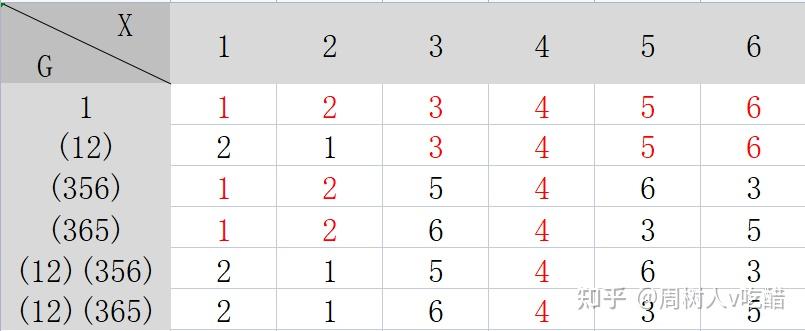
再给个例子。集合 \(X\) 是一个正六边形的 \(6\) 个顶点,按顺时针排序分别为 \(\{A_1,A_2,A_3,A_4,A_5,A_6 \}\)。\(G\) 中的元素有 \(\{60^{\circ},120^{\circ},180^{\circ},240^{\circ},300^{\circ},360^{\circ} \}\) 旋转变换和对称变换。同样可以验证满足两个条件。
轨道
定义
集合 \(X\) 中的元素 \(x\) 的轨道为 \(\{g \cdot x | g \in G\}\),记作 \(G(x)\),并称为 \(x\) 的 \(G-\) 轨道。意思就是,把 \(G\) 里边所有元素作用在 \(x\) 上得到的所有结果组成了一个集合,就是轨道。
轨道里面的元素都属于 \(X\)。
性质
- 不同元素的 \(G?\) 轨道要么没有公共元素,要么重合。也就是不同的轨道是集合 \(X\) 的一个划分。这不难想,挺显然的。
- 同一条轨道上的元素可以通过 \(G\) 中作用互相得到,不同轨道中的元素不能通过 \(G\) 中作用互相得到 \((\)就是定义中的封闭性\()\)。
稳定子群
定义
集合 \(X\) 中的元素 \(x\) 的稳定子群为 \(\{g|g \cdot x=x , g \in G\}\),记作 \(G_x\)。意思就是,作用在 \(x\) 上保持 \(x\) 不变的那些 \(g\) 组成的集合,而且可以证明这个集合 \((\)连带运算\()\) 是 \(G\) 的子群。
轨道稳定子定理
意思就是,群的元素个数等于某个元素的轨道的阶乘上该元素稳定子群的阶。
证明
首先证明 \(G_x\) 是 \(G\) 的一个子群。
- 封闭性:若 \(f,g \in G_x\),则 \((g \circ f)(x)=g(f(x))=g(x)=x\),所以 \(g \circ f \in G_x\)。
- 结合律:因为 \(G\) 满足,所以 \(G_x\) 显然也满足。
- 单位元:直接恒等式代换。
- 逆元:若 \(f \in G_x\),则 \(f^{-1} (x)=f^{-1}(f(x))=(f^{-1} \circ f)(x)=x\),所以 \(f^{-1} \in G_x\)。
由拉格朗日定理得到 \(|G|=|G_x| \times [G:G_x]\)。也就是说证明 \(|G(x)|=[G:G_x]\) 就可以了,根据轨道的性质 \(1\) 和陪集的性质 \(5\) 以及它们定义相似,这显然是正确的。
\(burnside\) 引理
设 \(X/G\) 表示 \(X\) 的不同 \(G-\) 轨道的集合,则我们有:
其中 \(X_g=\{x|g(x)=x,x \in X \}\),也即 \(X\) 在 \(g\) 置换下的不动点集合。
文字描述:\(X\) 关于置换群 \(G\) 的轨道数,等于 \(G\) 中每个置换下不动点的个数的算术平均数。
证明
根据轨道稳定子定理,我们有 \(|G|=|G_x| \times |G(x)|\),所以:
\(Pólya\) 定理
在实际做题情境中,我们假设有 \(A,B\) 两个有限集合。\(X\) 表示的是 \(A\) 到 \(B\) 的所有映射,\(G\) 表示作用在 \(A\) 上的一个置换群,那么就有:
其中 \(c(g)\) 表示置换 \(g\) 拆出的不相交轮换数量。
这在具体情境中的表现为:设 \(A=\{1,2,\cdots,n \}\) 是需要被染色物体的集合,有 \(|B|\) 种不同的颜色,\(G=\{g_1,g_2,\cdots,g_k \}\) 是 \(A\) 上的置换群,则在 \(G\) 的作用下本质不同的着色方案数是:
证明
在 Burnside 引理中,\(g(x)=x\) 的充要条件是 \(x\) 将 \(g\) 中每个轮换内的元素都映射到了 \(B\) 中的同一个元素,所以 \(|X_g|=|B|^{c(g)}\)。
注意只有当 \(X\) 是 \(A\) 到 \(B\) 的所有映射时,该定理才成立。
\(Pólya\) 计数
例子
题目
现在有一串共四个珠子的项链,每个珠子可以是红色或者蓝色,计算共有几种本质不同的珠子。如果两种染色的结果可以通过旋转项链重合,就认为是相同的。
解析
显然四个珠子对应着 \(A\),红色和蓝色对应着 \(B\)。不考虑本质不同,显然项链的染色方案共计 \(2^4=16\) 种,这 \(16\) 种染色方案对应着 \(X\)。将可以通过旋转相互得到的分到一组,共计 \(6\) 组,如下图所示:

从这个例子中可以看到,要计算本质不同的染色的种类数,关键其实是知道每种本质相同的染色对应几种不同的染色方案。也就是说,要搞清楚上图中每个分组的大小。
能够分到同一个组中的染色方案,就是指它们之间能够通过旋转操作互相转化的染色方案。总共有?\(4\)?种旋转的方式,即
分别表示旋转了 \(0,1,2,3\) 次。而它们的集合 \(G\) 可以看作是一个置换群。
首先看染色方案 \(RRBB\) 所在的分组,对它施加这四种操作,将分别得到 \(RRBB,BRRB,BBRR,RBBR\)。四种染色方案互不相同,因此这一组就有 \(4\) 个元素。
再看染色方案 \(BRBR\) 所在的分组,对它施加这四种操作,将分别得到 \(BRBR,RBRB,BRBR,RBRB\)。其中旋转两次和不旋转的结果相同,旋转三次和旋转一次的结果相同,所以这一组就有 \(2\) 个元素。
如果 \(x\) 表示某个染色方案,那么 \(G\) 的操作对于 \(x\) 有某一种周期性。如果有 \(m\) 个不同的 \(G\) 中的操作将 \(x\) 变换到它自身,那么 \(x\) 在这些操作下的结果就会重复出现 \(m\) 次。因而,染色方案 \(x\) 在这些操作下共计有 \(\frac{|G|}{m}\) 种不同的结果。如在上述例子中,因为只有旋转 \(0\) 次才能将 \(RRBB\) 变成它自身,所以他所在的分组大小等于 \(\frac{4}{1}=4\)。而旋转 \(0\) 次或旋转 \(2\) 次都能将 \(BRBR\) 变换到它自身,所以它所在的分组大小就是 \(\frac{4}{2}=2\)。
在下面的叙述中,用 \(G_x\) 表示能够将 \(x\) 变换到它自身的操作的数目,也就是上面的 \(m\)。\(Gx\) 表示对染色方案 \(x\) 操作后能够得到的颜色编码的集合。要计算染色方案的分组的数目,只需要穷举所有可能的染色方案 \(x \in X\),对所在分组大小为 \(|G_x|\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号