生成函数学习笔记
对于序列 \(a_0,a_1,\cdots\),构造函数 \(F(x)=a_0+a_1x+a_2x^2+\cdots\),称 \(F(x)\) 为序列 \(a_0,a_1,\cdots\) 的生成函数,也称母函数。
\(a\) 可以是有穷序列,也可以是无穷序列。
生成函数可以是一个无穷级数。我们一般设 \(-1<x<1\),在这个范围内,无穷级数收敛,可以在 \(x\to \infty\) 时得到该无穷级数的值。
(级数:将数列的项依次用加号连接起来的函数)
生成函数是一种幂级数,其中每项系数反映了这个序列的信息。
生成函数将方案数的序列映射成一个多项式的系数,将计数问题转化为多项式问题。
例 1
有三个砝码,分别为 \(1,2,3\) 克,问能够称出多少种不同的重量。
定义 \(a_i\) 表示称出 \(i\) 克的方案数。
- 考虑只有 \(1\) 克砝码的情况,组成 \(0\) 克有 \(1\) 种情况,\(a_0=1\),组成 \(1\) 克有一种情况,对应生成函数 \(f_1(x)=a_0+a_1x=1+x\)。
- 考虑只有 \(2\) 克砝码的情况,\(a_0=1,a_1=0,a_2=1\),所以对应生成函数 \(f_2(x)=1+x^2\)。
- 考虑只有 \(3\) 克砝码的情况,\(f_3(x)=1+x^3\)。
根据乘法原理,将三个生成函数相乘。
\(f_1(x)f_2(x)f_3(x)=(1+x)(1+x^2)(1+x^3)=1+x+x^2+2x^3+x^4+x^5+x^6\)。
其中 \(x^i\) 的系数代表称出 \(i\) 克的方案数。
例 2
现在有 \(n\) 种不同的苹果,每种苹果都有无限个,问选出 \(k\) 个苹果的方案数是多少。
组合数学解法
设 \(x_i\) 表示选第 \(i\) 种苹果的数量,那么需要满足 \(x_1+x_2+\cdots+x_n=k\),\(x_i\ge 0\)。
问题转化为这个方程的非负整数解的数量,根据插板法,显然 \(\binom{n-1}{k+n-1}\)。
生成函数解法
定义 \(a_i\) 表示选出 \(a_i\) 个苹果的方案数。
对于第 \(i\) 种苹果,对应的生成函数为 \(f_i(x)=1+x+x^2+\cdots=\lim\limits_{n\to \infty}\frac{1-x^n}{1-x}\)。
则 \(f_i(x)=\frac{1}{1-x}\),后面会推。
根据乘法原理,最终的生成函数为:\(f(x)=f_1(x)f_2(x)\cdots f_n(x)=\frac{1}{(1-x)^n}=\sum\limits_{k=0}^{\infty}\binom{k}{n+k-1}x^k\),答案为 \(x^k\) 的系数,即 \(\binom{k}{n+k-1}\)。
生成函数的解法
- 将原问题分解成若干个子问题。
- 求每个子问题的生成函数。
- 所有子问题生成函数相乘,系数加起来就是总方案数。
普通生成函数
序列 \(a\) 的普通生成函数定义为形式幂级数:
序列 \(a\) 既可以是有穷序列,也可以是无穷序列。
封闭形式
展开形式:\(1+x+x^2+\cdots\)
封闭形式:\(\frac{1}{1-x}\)。
通常在计算过程中,会适时将展开形式转换为封闭形式。
一般转化方式
有限序列 \(a\) 显然是容易的,这里讨论无限序列 \(a\) 的生成函数的转化方式。
e.g. \(F(x)=1+x+x^2+\cdots\),则 \(F(x)x+1=F(x)\),解方程得 \(F(x)=\frac{1}{1-x}\)。
常见形式幂级数
- \(\frac{1}{1-x}=\sum\limits_{i=0}^{\infty}x^i=1+x+x^2+\cdots\)
- \(\frac{x}{1-x}=\sum\limits_{i=0}^{\infty}x^{i+1}=x+x^2+x^3+\cdots\)
- \(\frac{1}{(1-x)^2}=\sum\limits_{i=0}^{\infty}(i+1)x^i=1+2x+3x^2\)
- \(\frac{1}{(1-x)^n}=\sum\limits_{k=0}^{\infty}\binom{k}{n+k-1}x^k\)
指数级生成函数
普通型生成函数可以用于求组合方案数。
指数级生成函数可以用于求排列数。
序列 \(a\) 的指数生成函数定义为形式幂级数:
\(a_i\) 表示选 \(i\) 个的派列数。
现在有序列 \(a\) 和序列 \(b\) 的指数生成函数:\(F(x)=\sum\limits_{n}a_n\frac{x^n}{n!}\),\(G(x)=\sum\limits_{n}b_n\frac{x^n}{n!}\)。
那么:

常见指数型生成函数转化
泰勒展开:
扩展:
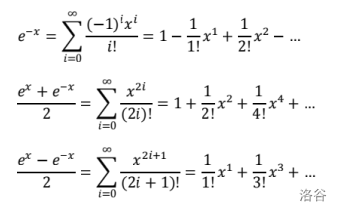



 浙公网安备 33010602011771号
浙公网安备 33010602011771号