广义后缀自动机（广义 SAM）学习笔记

dfs 有些东西我还没搞明白，并且离线 bfs 已经能解决绝大多数问题了，就没写 dfs 版本。

前置知识

后缀自动机、Trie。

用途

简单来讲，后缀自动机处理单个字符串的子串问题，广义后缀自动机则是处理多个字符串的子串问题。

定义

具体来说，对 \(T\) 个字符串 \(s_1,\cdots,s_T\) 建立一个 DFA：

状态和转移的定义等同 SAM。
这个 DFA 仅接受所有 \(s_i\) 的后缀。
和 SAM 类似的，一个状态不能有两个同为字符 \(c\) 的转移。
本质上是对这 \(T\) 个字符串的 Trie 建立 SAM。

在题目中，通常给出 \(T\) 个字符串，少数会给出 Trie。

在第二种情况中，一个结点数 \(m\) 的 Trie 最多可以对应 \(m^2\) 级别的，许多伪广义后缀自动机（后文会提到）的构造中，其复杂度依赖 \(\sum s_i\)，此时就需要用广义后缀自动机解决。

因为这个地方的定义改变，则需要重新理解几个概念。

定义 Trie 的根节点编号 \(0\)。

伪广义后缀自动机

指一类类似广义后缀自动机的解题思路，在上文（指 SAM）中提到过。

通常，伪广义后缀自动机有两种，我比较喜欢用第一种（也只用过第一种）：

通过特殊符号将多个串连接，对大串建立 SAM。
对每个串，重复在一个 SAM 上建立，每次建立前将 \(last\) 返回源点 \(t_0\)（\(last\gets 0\)）。

这两种解题思路在大多数题中可以使用，时间复杂度约 \(O(\sum s_i)\)。但某些题目中会直接给出 Trie（ZJOI2015 诸神眷顾的幻想乡），于是做不了。

后缀

定义 \(S\) 为 Trie 树，\(S_{x,y}\) 为 Trie 上 \(x\) 到 \(y\) 的简单路径上组成的字符串。

则 \(s_1,\cdots,s_T\) 的后缀可表示为 \(\{ S_{x,y}\mid y\in \text{subtree}(x),y\ \text{is leaf}\}\)。

endpos

定义一个字符串 \(s\) 的 \(\operatorname{endpos}\) 为一个集合，代表 \(s\) 在 Trie 上出现的路径中深度最深的结点编号，即 \(\operatorname{endpos}(s)=\{y\mid y\in \text{subtree}(x),S_{x,y}=s\}\)。

后缀链接

和 SAM 一致。

构造

感觉本质上来说和伪广义后缀自动机第二行种差不多，只是通过用字典树的方式使得没有两个同样的字符转移了，可以避免 空节点 问题。

空结点问题

用伪广义后缀自动机时会出现的一类问题：

比如对于一个字符串 \(ab\) 的后缀自动机，加入一个字符串 \(b\)（图是薅过来之后改了一下的）：

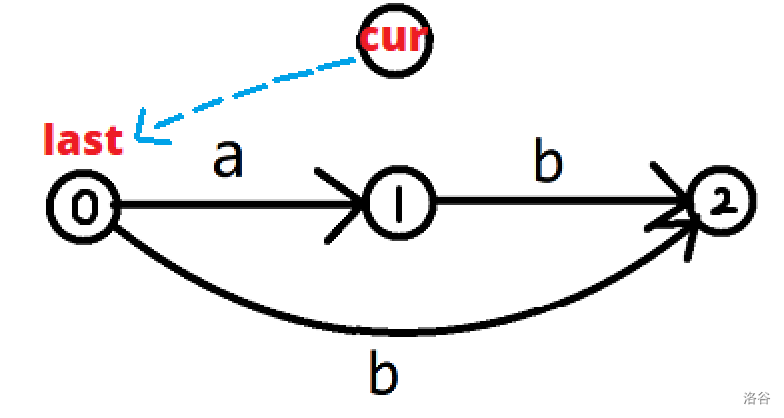
因为此时 \(cur\) 这个结点没有边，所以就成空结点了。某些问题中这不影响最终答案，但在比如模板中点数计数等问题中就不合法了。

Part 1

如果题目直接给 Trie 就不存在这个步骤。

如果没有，则需要将所有字符串或者其他东西（比如一棵普通的树，P3346）变为一个 Trie。

代码和普通的将字符串插入进 Trie 中没有区别。

struct Tire
{
	sd map<int,int> nex;
	int fa;
	char c;//c记录和父亲的边是哪个字母
}t[N];
int id;
void insert(char *s)
{
	int len=strlen(s+1),p=0;
	F(i,1,len)
	{
		int &cur=t[p].nex[s[i]];
		if(!cur) cur=++id,t[cur].fa=p,t[cur].c=s[i];
		p=cur;
	}
}

Part 2

对于一个字符的插入，为了方便，我们在末尾返回它的结点编号。

其他的和普通 SAM 没啥区别。

struct state
{
	int link,len;
	sd map<int,int> nex;
}st[N];
int siz;
void init()
{
	st[0].link=-1;
	st[0].len=0;
	siz=1;
}
int extend(char c,int last)
{
	int p=last,cur=siz++;
	while(p!=-1&&!st[p].nex.count(c))
	{
		st[p].nex[c]=cur;
		p=st[p].link;
	}
	if(p==-1)
	{
		st[cur].link=0;
	}
	else
	{
		int q=st[p].nex[c];
		if(st[q].len==st[p].len+1)
		{
			st[cur].link=q;
		}
		else
		{
			int nw=siz++;
			st[nw].link=st[q].link;
			st[nw].nex=st[q].nex;
			st[nw].len=st[p].len+1;
			while(p!=-1&&st[p].nex[c]==q)
			{
				st[p].nex[c]=nw;
				p=st[p].link;
			}
			st[cur].link=st[q].link=nw;
		}
	}
	return cur;
}

Part 3

接下来需要对这个 Trie 构造广义后缀自动机。

主要有三种办法：离线 bfs，离线 dfs，在线 dfs。离线和在线分别指对一棵完整的 Trie 构造广义后缀自动机以及对每个字符串动态的加入。

这里只提到离线 bfs，它已经可以应付绝大多数问题。

其实差不多就是模拟，用数组 \(pos_u\) 代表 Trie 上结点对应的状态，每次从 \(pos_{fa_u}\) 状态处插入字符。

int pos[N];//记录字典树上某结点对应到的状态
sd queue<int> q;
void built()
{
	Fr(t[0].nex) q.push(it.Y);
	pos[0]=0;
	while(!q.empty())
	{
		int u=q.front();q.pop();
		pos[u]=extend(t[u].c,pos[t[u].fa]);
		Fr(t[u].nex) q.push(it.Y);
	}
}

然后就完了。

Code（离线 bfs）

完整代码（发现原本那个代码过不去，得把 map 换成数组）

#include<bits/stdc++.h>
#define sd std::
// #define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define f(i,a,b) for(int i=(a);i>=(b);i--)
#define MIN(x,y) (x<y?x:y)
#define MAX(x,y) (x>y?x:y)
#define me(x,y) memset(x,y,sizeof x)
#define pii sd pair<int,int>
#define X first
#define Y second
#define Fr(a) for(auto it:a)
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=1e6+10;
int n;
struct Tire
{
	int nex[26];
	int fa,c;//c记录和父亲的边是哪个字母
}t[N];
int id;
void insert(char *s)
{
	int len=strlen(s+1),p=0;
	F(i,1,len)
	{
		int &cur=t[p].nex[s[i]-'a'];
		if(!cur) cur=++id,t[cur].fa=p,t[cur].c=s[i]-'a';
		p=cur;
	}
}
struct state
{
	int link,len;
	int nex[26];
}st[N<<1];
int siz;
void init()
{
	st[0].link=-1;
	st[0].len=0;
	siz=1;
}
int extend(int c,int last)
{
	int p=last,cur=siz++;
	st[cur].len=st[last].len+1;
	while(p!=-1&&!st[p].nex[c])
	{
		st[p].nex[c]=cur;
		p=st[p].link;
	}
	if(p==-1)
	{
		st[cur].link=0;
	}
	else
	{
		int q=st[p].nex[c];
		if(st[q].len==st[p].len+1)
		{
			st[cur].link=q;
		}
		else
		{
			int nw=siz++;
			st[nw].link=st[q].link;
			F(i,0,25) st[nw].nex[i]=st[q].nex[i];
			st[nw].len=st[p].len+1;
			while(p!=-1&&st[p].nex[c]==q)
			{
				st[p].nex[c]=nw;
				p=st[p].link;
			}
			st[cur].link=st[q].link=nw;
		}
	}
	return cur;
}
int pos[N];//记录字典树上某结点对应到的状态
sd queue<int> q;
void built()
{
	F(i,0,25) if(t[0].nex[i]) q.push(t[0].nex[i]);
	pos[0]=0;
	while(!q.empty())
	{
		int u=q.front();q.pop();
		pos[u]=extend(t[u].c,pos[t[u].fa]);
		F(i,0,25) if(t[u].nex[i]) q.push(t[u].nex[i]);
	}
}
char s[N];
void solve()
{
	n=read();
	F(i,1,n)
	{
		scanf("%s",s+1);
		insert(s);
	}
	init();
	built();
	long long ans=0;
	F(i,1,siz-1) ans+=1ll*st[i].len-1ll*st[st[i].link].len;
	printf("%lld\n%d",ans,siz);
}
int main()
{
	int T=1;
//	T=read();
	while(T--) solve();
    return 0;
}

至于在线的，后面我有时间再补。

例题

ZJOI2015 诸神眷顾的幻想乡

拼尽全力切不掉。可能我对 SAM 还是不怎么熟。

PS：题目中最后一句说的是叶节点个数不超过 20 个，我断句错了读成了一个结点的相邻结点不超过 20 个。

难点是把一颗树扔到字典树上，使得这颗字典树的后缀包含这颗树的所有 \(A\to B\) 的路径。

这里有一个结论：

对于一棵树的一条路径 \(A\to B\)，一定存在某个叶节点，使得它为根的时候这个路径被表示为一颗从上到下的路径。

于是暴力枚举叶节点作为根，把最多 \(20\) 棵 Trie 合并到一个 Trie 上即可。

然后是板子。注意 Tire 的插入，插入一棵树要一个字符一个字符插入，需要记录一下树上结点对应到 Tire 上的节点编号。

#include<bits/stdc++.h>
#define sd std::
//#define int long long
#define F(i,a,b) for(int i=(a);i<=(b);i++)
#define f(i,a,b) for(int i=(a);i>=(b);i--)
#define MIN(x,y) (x<y?x:y)
#define MAX(x,y) (x>y?x:y)
#define me(x,y) memset(x,y,sizeof x)
#define pii sd pair<int,int>
#define X first
#define Y second
#define Fr(a) for(auto it:a)
#define dbg(x) sd cout<<#x<<":"<<(x)<<"\n";
int read(){int w=1,c=0;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) c=(c<<3)+(c<<1)+ch-48;return w*c;}
void printt(int x){if(x>9) printt(x/10);putchar(x%10+48);}
void print(int x){if(x<0) putchar('-'),printt(-x);else printt(x);}
void put(int x){print(x);putchar('\n');}
void printk(int x){print(x);putchar(' ');}
const int N=2e6+10;
int id[N],w[N];
struct SAM
{
	struct Trie
	{
		int nex[10];
		int fa,c;
	}t[N];
	int num;
	void insert(int u,int fa)
	{
		int &to=t[fa].nex[w[u]];
		if(!to) to=++num,t[to].fa=fa,t[to].c=w[u];
		id[u]=to;
	}
	struct state
	{
		int link,len;
		int nex[10];
	}st[N];
	int siz;
	void init()
	{
		st[0].link=-1;
		st[0].len=0;
		siz++;
	}
	int extend(int c,int last)
	{
		int cur=siz++,p=last;
		st[cur].len=st[last].len+1;
		while(p!=-1&&!st[p].nex[c])
		{
			st[p].nex[c]=cur;
			p=st[p].link;
		}
		if(p==-1)
		{
			st[cur].link=0;
		}
		else
		{
			int q=st[p].nex[c];
			if(st[q].len==st[p].len+1)
			{
				st[cur].link=q;
			}
			else
			{
				int nw=siz++;
				st[nw].len=st[p].len+1;
				F(i,0,9) st[nw].nex[i]=st[q].nex[i];
				st[nw].link=st[q].link;
				while(p!=-1&&st[p].nex[c]==q)
				{
					st[p].nex[c]=nw;
					p=st[p].link;
				}
				st[cur].link=st[q].link=nw;
			}
		}
		return cur;
	}
	int pos[N];
	sd queue<int> q;
	void built()
	{
		F(i,0,9) if(t[0].nex[i]) q.push(t[0].nex[i]);
		pos[0]=0;
		while(!q.empty())
		{
			int u=q.front();q.pop();
			pos[u]=extend(t[u].c,pos[t[u].fa]);
			F(i,0,9) if(t[u].nex[i]) q.push(t[u].nex[i]);
		}
	}
}sa;
struct node
{
	int nex,to;
}a[N<<1];
int tot,head[N];
void add(int u,int v)
{
	a[++tot].nex=head[u];
	head[u]=tot;
	a[tot].to=v;
}
void dfs(int u,int fa)
{
	sa.insert(u,id[fa]);
	for(int i=head[u];i;i=a[i].nex)
	{
		int v=a[i].to;
		if(v==fa) continue;
		dfs(v,u);
	}
}
int n,c;
int d[N];
void solve()
{
	n=read();c=read();
	F(i,1,n) w[i]=read();
	F(i,1,n-1)
	{
		int x=read(),y=read();
		add(x,y);
		add(y,x);
		d[x]++,d[y]++;
	}
	F(i,1,n) if(d[i]==1) dfs(i,0);
	sa.init();
	sa.built();
	long long ans=0;
	F(i,1,sa.siz-1) ans+=sa.st[i].len-sa.st[sa.st[i].link].len;
	printf("%lld",ans);
}
int main()
{
	int T=1;
//	T=read();
	while(T--) solve();
    return 0;
}

练习题

link。

参考资料

博客园-广义后缀自动机（广义 SAM）学习笔记

oiwiki-广义后缀自动机

posted @ 2025-01-03 20:55 _E_M_T 阅读(108) 评论(0) 收藏举报

刷新页面返回顶部

E_M_T

我永远喜欢Emilia!