后缀自动机学习笔记
本文抄写自 OIwiki 是对 OIwiki 的注解。
用途
以合并部分子串的方式,储存字符串所有的子串。
根本思想
有一种数据结构叫作后缀树。它的思想是:将所有后缀插入字典树。如下。
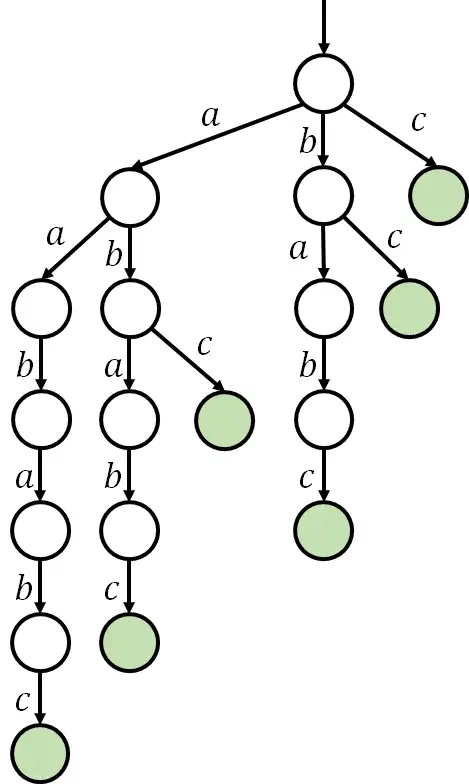
容易发现它有非常多的部分是重复的。
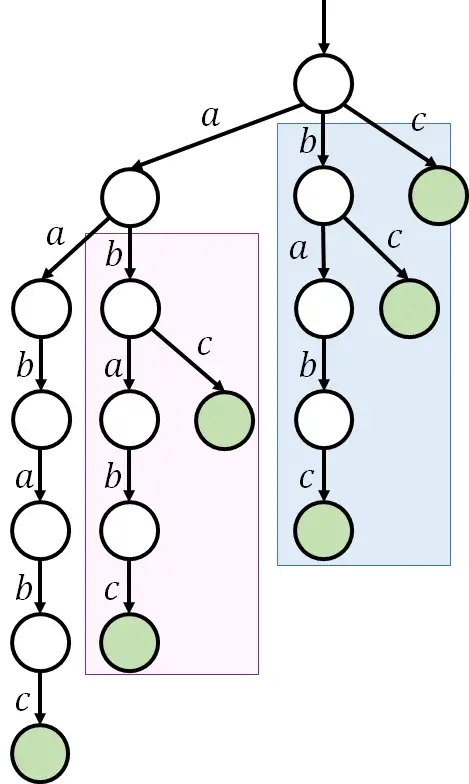
于是,为了消除此类冗余,将字典树的结构修改为图,便有了 SAM。
引自知乎
概念阐释
-
endpos:这是一个集合。\(endpos(x)\) 代表子串 \(x\) 在 \(s\) 中所有结束位置的集合。
-
等价类:这也是一个集合。一个等价类中包含所有 \(endpos(i)\) 完全相等的子串 \(i\)。
有如下引理(其实很显然,看了理解了就可以了):
-
同一等价类中,子串绝对存在后缀包含关系。
-
若子串 \(u\) 为子串 \(v\) 的后缀,\(endpos(u)\) 被包含于 \(endpos(v)\);否则二者的 \(endpos\) 无交。
-
同一等价类中,串的长度绝对连续,且没有重复。
接下来是有关 SAM 构建的概念。
-
SAM 本身:和其他自动机一样,以字典树结构为主体——或者更应该说是字典图,是一个 DAG。它的更为严谨的定义是:一个接受 \(s\) 的所有后缀的最小 DFA。
-
SAM 中的节点:代表一个等价类。而它在 SAM 图中距离原点最长的路径代表着 “该等价类中的最长子串”,下文将该字串记为 \(w\)。
-
原点:代表空串的节点 0。
-
终止状态:由于 SAM 是一个 DFA,它的终止状态即为字符串 \(s\) 的所有后缀。在算法的最后我们会介绍怎么设置终止状态。
-
len:每个节点上储存的数据。代表 \(w\) 的长度,也代表 SAM 图上原点到该节点的最长距离。
-
后缀链接(link):每个节点上储存的数据。类似其它自动机的 fail。它指向 \(w\) 最长的一个后缀,which 满足不在该等价类中。容易发现,后缀链接可构成一棵以 0 为根的树。
-
转移边:每个节点上储存的数据。就是普通字典树边,储存字符信息。
引自 OIwiki | 左图为 SAM 图,右图为 link 形成的树
算法过程
同其它自动机一样,也是在线地一个一个插入字符。
设插入前的字符串为 \(s\)。对于当前字符 \(c\),算法流程如下:
-
令 \(last\) 为添加字符 \(c\) 之前,\(s\) 所在等价类对应的节点。
-
创建新节点 \(cur\),代表串 \(s+c\) 所在等价类,将 \(len(cur)\) 赋值为 \(len(last)+1\)。
-
从 \(last\) 开始,循环跳 \(link\)。记当前遍历到的节点为 \(p\),每次执行如下:
-
如果 \(p\) 不存在字符 \(c\) 的转移,则将 \(c\) 转移指向 \(cur\),并继续循环。(将新子串添加到 \(cur\) 等价类内。)
-
否则,现在及之前的字符 \(c\) 转移都已经赋值完成。设 \(p\) 的 \(c\) 转移指向节点 \(q\)。
此时显然无法再将任何子串加入 \(cur\) 等价类了。现在的首要任务是:
-
通过分析,找出 \(link(cur)\) 所对应的值。
-
分析 \(p\) 所代表的等价类在加上了字符 \(c\) 之后发生的变化:可能,有的子串因为新增的 \(c\),加入了新的等价类;而有的保持在原本的等价类。
因此,需要再分两种情况:
-
如果 \(len(p)+1 = len(q)\),这说明原点到 \(q\) 的所有路径中(也就是等价类 \(q\) 所包含的所有子串中),经过 \(p\) 的这一条路径刚好是最长的那一条(最长子串)。此时,即使加入了新字符 \(c\),也不会产生新的等价类。因此直接将 \(link(cur)\) 指向 \(q\) 即可。
-
否则则一定产生了一个新的等价类,它的最长子串就是经过转移边 \((p, q)\) 的路径。
于是就创建一个新的状态 \(clone\),复制 \(q\) 除 \(len\) 以外的所有信息(后缀链接和转移),并将 \(len(clone)\) 赋值为 \(len(p)+1\)。
复制之后,将 \(link(cur)\) 指向 \(clone\),也将 \(link(q)\) 指向 \(clone\)。
最终需要做的是修改一些原本指向 \(q\) 的转移边。具体地,对于一个点 \(x\),如果 \(len(x)+1 < len(clone)\) 则将转移边指向 \(clone\),否则则保持它指向 \(q\)(利用等价类长度连续的引理)。容易发现,只要继续从 \(p\) 开始跳 \(link\),就能够找到每一个满足 \(len(x)+1 < len(clone)\) 的 \(x\)(跳 \(link\) 时,\(len\) 单调递减,故 \(len(x)+1 < len(p)+1 = len(clone)\))。
-
-
-
在跳到 \(link(0) = -1\) 这个虚拟节点时,停止循环。将 \(last\) 的值更新为 \(cur\)。
最后提一下怎么设置“终止状态”(即代表字符串所有后缀的节点):从代表整个字符串的节点开始,往上跳后缀链接 \(link\),遇到的所有节点设为终止状态。一般来说,可以忽略这一个操作。
复杂度证明
如果我们考虑算法的各个部分,算法中有两处时间复杂度不明显是线性的:
-
第一处是遍历所有状态 \(last\) 的后缀链接,添加字符 \(c\) 的转移。
-
第二处是修改指向 \(q\) 的转移,将它们重定向到 \(clone\) 的过程。
第一处显然可以用均摊证明整体的 \(O(n)\) 复杂度。
第二处的复杂度需要用到一个结论:总转移数的上界为 \(3n\)。(证明 没看懂,咕了。。。)
回过来看第二处的复杂度证明。明显复杂度等价于指向 \(clone\) 的转移数,而 \(clone\) 不会重复遍历,因此第二处的均摊复杂度等价于总转移数,为 \(O(n)\)。
应用
1. 每个子串出现次数
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e6+5;
int n, tot;
char s[MAXN];
vector<int> ord[MAXN];
struct Trie{
int link, len, sz, ch[26];
#define sz(x) tree[x].sz
#define len(x) tree[x].len
#define link(x) tree[x].link
#define ch(x, y) tree[x].ch[y]
} tree[MAXN<<1];//注意因为有复制操作,要两倍大小
int main(){
scanf("%s", s+1);
n = strlen(s+1);
link(0) = -1;
int p = 0;
for(int i = 1; i <= n; i++){
int c = s[i]-'a', cur = ++tot;
len(cur) = len(p)+1, sz(cur) = 1;
for(; p != -1 and !ch(p, c); p = link(p)) ch(p, c) = cur;
if(p != -1){
int q = ch(p, c);
if(len(p)+1 == len(q)) link(cur) = q;
else{
int clone = ++tot; tree[clone] = tree[q];
len(clone) = len(p)+1, sz(clone) = 0;
link(cur) = link(q) = clone;
for(; p != -1 and ch(p, c) == q; p = link(p)) ch(p, c) = clone;
// 每个不同的 ch(p, c) 在树链上是连续的颜色段
}
}
p = cur;
}
ll ans = 0;
for(int i = 1; i <= tot; i++) ord[len(i)].push_back(i);
for(int i = n; i >= 1; i--)
for(int j = 0; j < ord[i].size(); j++){
int x = ord[i][j];
sz(link(x)) += sz(x);
if(sz(x) > 1) ans = max(ans, 1ll*len(x)*sz(x));
}
cout<<ans;
return 0;
}
/*
利用“前缀的后缀就是所有子串”(或者说,一个新增点肯定是与 link 链上的所有点形成新子串的 )
将所有表示前缀的节点(非复制节点,即正常插入的节点)的 size 设为 1
然后按照 link 形成的后缀链接树累加起来
*/
2. 不同子串个数
法一:DP 求 DAG 不同路径条数。(每个节点存储的 \(dp[i]\),实际表示从这个点开始的子串个数。)
法二:总数量 - 重复数量(上一题)。
法三:在线做法。观察可知,每插入一个新字符,它只与新增的转移边形成新的“不同子串”。于是每次连接转移 \((p, cur)\) 时,使 ans 加上 \(len(p) - len(link(p))\) 即可。
P4070 [SDOI2016] 生成魔咒:用 map 对转移边储存进行优化。
3. 第 k 大的子串
运用上一题中的 dp 数组,预处理完成后进行扫描即可。
4. 最长公共子串
【待补】
对比
-
与后缀数组对比:
-
与 AC 自动机对比:
广义后缀自动机
广义后缀自动机是用来解决多模式串匹配的一个工具。以下题为例:
给定 \(n\) 个由小写字母组成的字符串 \(s_1, s_2, \dots, s_n\),求它们的所有本质不同子串的个数。
网上流传的主流写法有三种:
-
通过用特殊符号将多个串直接连接后,再建立 SAM。
-
对每个串,重复在同一个 SAM 上进行建立,每次建立前,将 last 指针置零。
-
(正解)用所有模式串建出一棵 Trie 树,对其进行 bfs 遍历构建 SAM,insert(x) 时以 x 在 Trie 上的父亲为 last,其余和普通 SAM 一样。
【弄不懂为什么第一种有错。复杂度难道不是线性的吗?抑或是说是插入特殊符号的特判出了问题?】
第二种其实是可以的,但需要加上一些特判。 这篇博客 中给出了对于不加特判的情况的卡掉的方案。
在讨论第三种之前先研究一下第二种法案建出来的 SAM 图。这时图中的每个节点已不再是一个等价类了,而是 等价类的集合。如下图,每个节点旁有两个花括号,每个花括号内都是一个不同的模式串的等价类。这样问题就被扩展了。
【感觉我这里还没有理解清楚……但是得先咕掉了……】
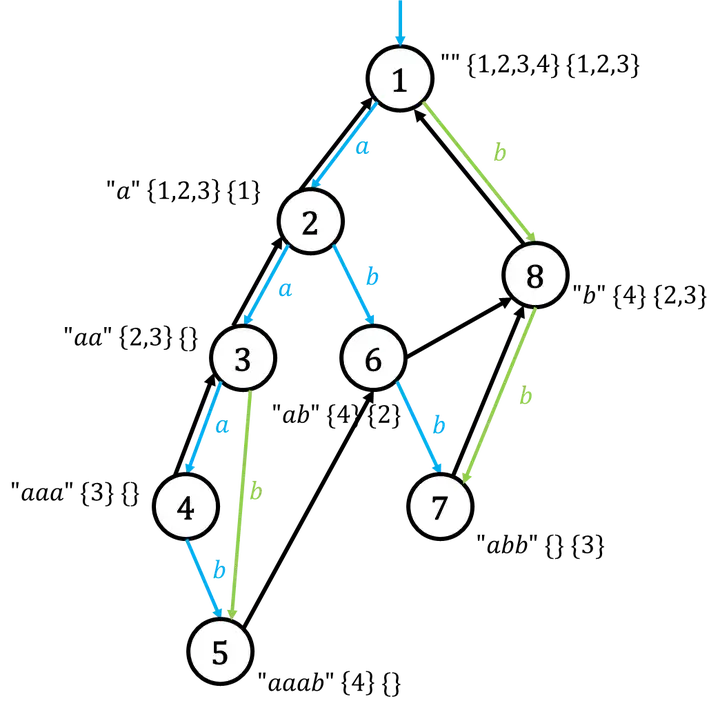
引自知乎
第三种本质上是对第二种的改进:第二种可能会重复建立一些节点,而使用 Trie 结构则去除了这些重复。这样建立的 DFA 可保证节点数量最小。(听说其实也可以用 dfs 而非 bfs,但是特判太多容易写挂,故不在此讨论。)
bfs 写法代码:
点击查看代码
inline void Insert_SAM(int p, int cur, int c){
//不用为 cur 新建节点。因为我们直接利用已经建好的那棵 Trie 树建立 SAM。
len(cur) = len(p)+1;
ans += p ? len(p)-len(link(p)) : 1;
//为了 ch(p, c) 能够进行,要从 link(p) 开始
for(p = link(p); p != -1 and !ch(p, c); p = link(p)){
ch(p, c) = cur;
ans += p ? len(p)-len(link(p)) : 1;
}
if(p == -1) return;
int q = ch(p, c);
if(len(q) == len(p)+1) {link(cur) = q; return;}
int clone = ++tot;
link(clone) = link(q);
for(int i = 0; i < 26; i++)
if(len(ch(q, i))) ch(clone, i) = ch(q, i);
//len 在这里实际用来判断一个节点是否已经被插入 SAM
len(clone) = len(p)+1;
link(cur) = link(q) = clone;
for(; p != -1 and ch(p, c) == q; p = link(p)) ch(p, c) = clone;
return;
}
inline void bfs(){
queue<int> que;
que.push(0); link(0) = -1;
while(!que.empty()){
int cur = que.front(); que.pop();
for(int i = 0; i < 26; i++){
if(!ch(cur, i)) continue;
Insert_SAM(cur, ch(cur, i), i);
que.push(ch(cur, i));
}
}
return;
}
还有一种写法,支持在线插入模式串。(其实就是上述的第二种加上了一些特判。)代码如下:
点击查看代码
inline void Insert(){
for(int i = 1, p = 0; i <= n; i++){
int c = s[i]-'a';
if(ch(p, c)){//如果想插入的位置已经存在节点了,不用新建
int q = ch(p, c);
//按照“等价类的集合”是否变动来决定是否拆分该节点
//(和普通 SAM 的判断操作其实是一样的)
if(len(p)+1 == len(q)) p = q;//last = q
else{
int clone = ++tot; tree[clone] = tree[q];
len(clone) = len(p)+1;
link(q) = clone;
for(; p != -1 and ch(p, c) == q; p = link(p)) ch(p, c) = clone;
p = clone;//last = clone
}
}
else{//剩下同普通 SAM
int cur = ++tot; len(cur) = len(p)+1;
for(; p != -1 and !ch(p, c); p = link(p)){
ch(p, c) = cur;
ans += p ? len(p)-len(link(p)) : 1;
}
if(p != -1){
int q = ch(p, c);
if(len(p)+1 == len(q)) link(cur) = q;
else{
int clone = ++tot; tree[clone] = tree[q];
len(clone) = len(p)+1;
link(q) = link(cur) = clone;
for(; p != -1 and ch(p, c) == q; p = link(p)) ch(p, c) = clone;
}
}
p = cur;
}
}
return;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号