字符串算法学习笔记

字符串算法的核心是关心子串。

——教练语。

一、基本概念

1. 自动机

自动机是什么？它是一个对“信息序列”进行判定的数学模型。“信息序列”可以很随意，比如一个二进制数，比如一个字符串。而“判定”也可以很随意，比如判定一个二进制数是不是奇数，判定当前字符串是不是某个字符串的子串。

它的本质是一个有向图。它里面的节点分为两种：“接受节点”和“不接受节点”，在哪个地方停下就说明是判定成功还是不成功。

具体的一个判定过程是这样的：从一个代表“空”的起始节点开始，逐步地往里面插入信息序列的每一个元素。直到插完了或是走不动了，就停下来，进行判定。

是不是很像 Trie？没错，Trie 就是一种自动机。下面的很多算法都是自动机。（不知道能不能这么说，因为 OIwiki 上说自动机是一种数学模型，不能等同于 data stracture、algorithm 之流……）

字符串自动机的基本套路：用于向末尾插入新节点时动态维护信息；大体是一个树的形状，但是有一个 fail 指针，用于失配之后跳向其后缀，即“如果这个串不行，就试试它的后缀可不可以”的思想。

二、基本工具

1. 进制哈希

用途：优化比较两个序列是否相等的效率，尤其是在有许多静态文本串时。

例题：

P3501 [POI2010] ANT-Antisymmetry：二分 + 哈希解决最长回文串问题。
P5537 【XR-3】系统设计：从使用二分将求最值转为判定的思路出发。发现如果加上每个节点到根的部分，我们就拥有了 n 个静态的文本串，就再用二分 + 哈希解决。而动态求序列哈希，可以使用树状数组 / 线段树解决。

2. Trie 字典树

用途：查询多个字符串 / 它们的前缀是否存在。

特殊类型：

01Trie：查询某数 x 与数集中数的最大异或值。
可持久化 01Trie：查询某数 x 与某区间中数的最大异或值。

例题：

P9218 「TAOI-1」Apollo：f 操作的实质是求出最长公共前缀，自然想到使用字典树来组织若干字符串。
P3294 [SCOI2016] 背单词：组织多个字符串之间的后缀包含关系，自然想到反建字典树。接着是两条性质：以 dfs 序贪心，优先遍历子树大小更小的。 具体证明可以点此，大致是使用了微扰法：link。
P4735 最大异或和：可持久化 01Trie 求区间异或最大值。
P3293 [SCOI2016] 美味：利用 01Trie 的思想，但以可持久化线段树为主体。（可持久化线段树的区间划分更灵活。）

三、回文类

1. Manacher

用途：求出字符串中以每个字符为中心的最长回文串长度。

过程：

大概就是一个充分利用已有信息的思想。

回文串分为奇、偶两种，在一开始在所有字符之间插入一个 #，将所有回文串转化为奇回文串。

从左往右枚举每个回文串的中心 $i$ 。令 $p_{i}$ 表示以 $i$ 为中心的回文串的半径长度。
维护一个当前已经更新到的最远右端点 $r$ ，和 $r$ 区间的中心 $c$ 。
找到 $i$ 关于 $c$ 的对称点 $j$ 。
如果 $i + p_{j} \leq r$ ， $p_{i} = p_{j}$ ，停止更新；
如果 $i + p_{j} > r$ ，暴力拓展 $p_{i}$ ，再更新 $c, r$ 。

每个点只被暴力拓展一次，复杂度 $O (n)$ 。

例题：

P3805 【模板】manacher
P4555 [国家集训队] 最长双回文串 & P4287 [SHOI2011] 双倍回文：某些字符串题考验的重点并不在结合能力，而在“套模板”（把当前问题设法转化为模板）。这两道题其实都可以证明得答案只有在暴力拓展时才能更新。

2. 回文树（回文自动机）

link

四、匹配类

1. KMP 自动机

用途：给定一个模式串，再给定一个文本串，求模式串在文本串中每次出现的位置。

过程：

nxt 数组：当前前缀中，前缀和后缀的最长匹配。
对于模式串，求出 nxt 数组：当不满足 $s [n x t_{j} + 1] = s [i]$ 时，不断跳 nxt。
对于模式串和文本串，无法匹配，就试试与模式串前缀匹配：当不满足 $s 2 [j + 1] = s 1 [i]$ 时，不断跳 nxt。

时间复杂度 $O (n + m)$ 。

例题：

P3375 【模板】KMP
P4824 [USACO15FEB] Censoring S：容易想到 KMP。本题的巧妙点在于：不在完整地进行了一次 KMP 后，利用处理得到的信息；而是在进行算法的过程中，顺势进行调整。
P5829 【模板】失配树：nxt 指针实际是构成一个树形结构的，这与前讲述的自动机的树形特性不谋而合。本题就是建树求 LCA 的过程。

2. 扩展 KMP

P5410 【模板】扩展 KMP/exKMP（Z 函数）

LCP：最长公共前缀

用途：求出某字符串与自身的每一个后缀的 LCP（又称 $z$ 函数）；求出字符串 $b$ 与字符串 $a$ 每一个后缀的 LCP。

过程：

主要过程就是求出 $b$ 的 $z$ 函数。而这一过程极为类似 Manacher。

存储当前扩展到的 $r$ 最大的区间 $[l, r]$ 。这个区间指的是 $[j, j + z [j] - 1]$ ，即与一个后缀 $j$ 的匹配。

然后先试着利用以前的信息，得到一个基础 $z [i]$ 。

如果 $i > r$ ：令 $z [i] = 0$ 。
如果 $i \in [l, r]$ ：关注 $[l, r]$ 所匹配上的 $b$ 的那个前缀区间（方才提了， $[l, r] = [j, j + z [i] - 1]$ ，所以该前缀区间即为 $[1, z [i]]$ ）。显然， $i$ 在前缀区间里面是有一个很相近的对应点的（类比 Manacher 里面的镜像点），易得： $z [i] = min {z [对应点], r - i + 1}$ 。
然后也像 Manacher 一样，暴力往后拓展 $z [i]$ ，均摊复杂度 $O (n)$ 。

最后，就当作把 $a$ 数组接到 $b$ 的后方，就可以很轻松地理解“ $b$ 与 $a$ 的每一个后缀的 LCP”的求法了。

【吐槽：这个算法除了要分别对模式串、文本串进行两次算法以外，和 KMP 有什么任何的联系吗？？？叫扩展马拉车都比这个合适吧？？？】

3. AC 自动机

用途：给定若干模式串与一个文本串，将所有模式串与文本串分别匹配。

复杂度：设字符串的最长长度为 $w$ ，有 $n$ 个模式串，文本串长度为 $m$ 。 $n$ 次 KMP 的复杂度为 $O (n m + n w)$ ，AC 自动机的复杂度为 $O (n w + m w)$ ，优化后可以达到 $O (n w + m)$ 。（因此，AC 自动机可用于处理 $n$ 非常大的情况。）

过程：

AC 自动机的主要思想是“字典树主结构 + KMP 附属结构”。

将所有模式串按照正常方式插入字典树。
fail 指针：这里的 fail 指针不完全等同于 KMP 中“对自身匹配”的 nxt，而是在整个字符串集中的匹配。每个 fail 指向当前字符串在整个字符串集中的那个最长后缀。为了求出 fail，可以在插入完毕以后，进行一次 bfs，每次从 $f a i l_{f a t h e r}$ 开始不断跳 fail，直到找到某个 $p$ 存在 $s o n_{p, s [i]}$
路径压缩：发现跳 fail 浪费了很多时间。那么我们提前路径压缩一下——如果某个儿子为空，就把它直接接向 fail 的对应儿子；每次跳 fail 时，也就只用将 fail 赋值为 $s o n_{f a i l_{f a t h e r}, s [i]}$ 。这样 bfs 的时间复杂度可被优化为 $O (n w)$ 。可以发现，此时的字典树更像字典图，而 fail 指针构成了一棵独特的树。

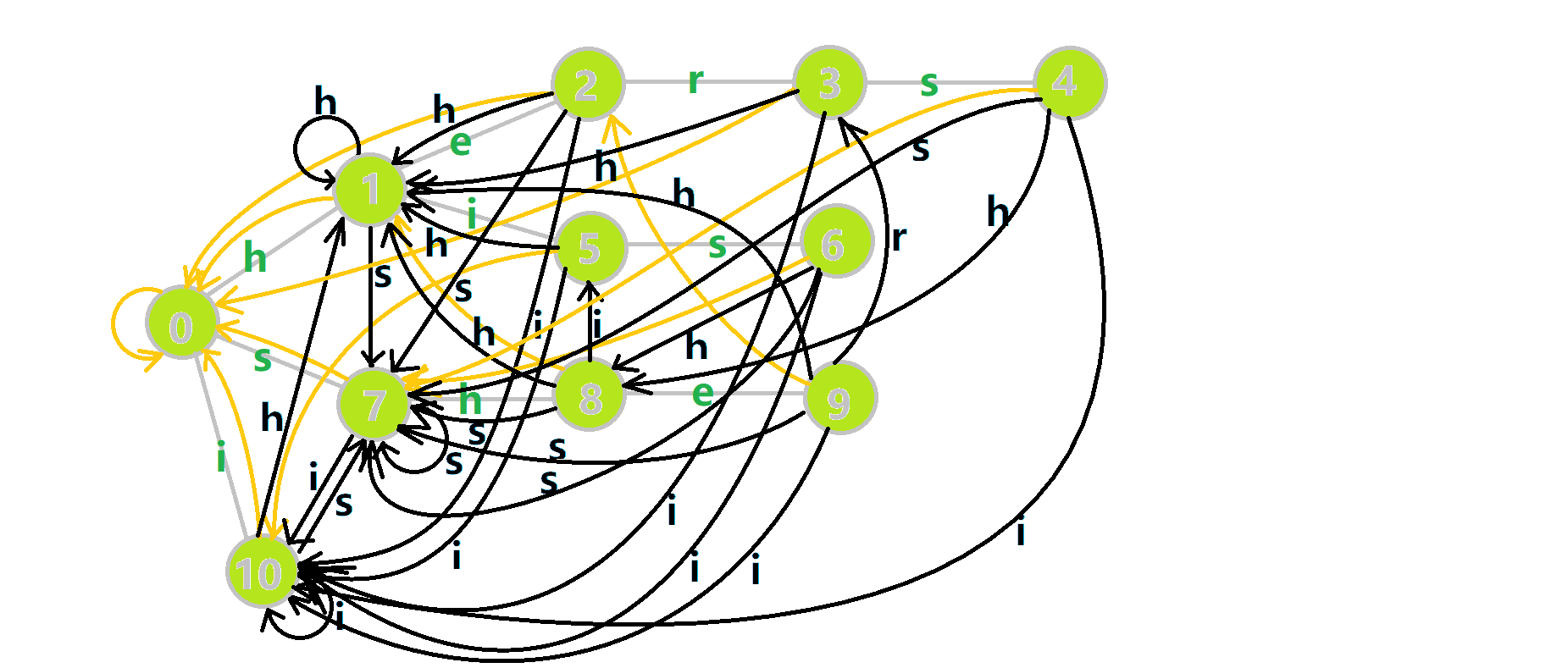
上图中，灰色边为原字典树边，黑色边为字典图新增边，黄色边为 fail 指针 $|$ 引自 OIwiki

朴素文本串匹配：在字典图上按照正常方式询问文本串。每次查询到一个节点时，不断跳 fail 直至到根节点，即可访问到所有匹配的串。由于路径压缩，失配 / 走到模式串尽头时，可以省略部分跳 fail；而查询到任意一个节点时都要跳 fail，可以理解为“所有前缀的所有后缀即为所有子串”。这个操作的复杂度为 $O (m w)$ ，主要瓶颈在跳 fail。
优化一：如 P3808 AC 自动机（简单版），可以标记避免重复跳，复杂度轻松优化至 $O (m + n w)$ 。
优化二：如 P5357 【模板】AC 自动机，可以先进行简略标记，最后 dfs 一次性扫描统计（或者按照 fail 边拓扑排序），复杂度也是 $O (m + n w)$ 。

实现注意：

0 节点的子节点的 fail 指针需要特判。最好在一开始 bfs 时直接插入队列。

例题：

以 AC 自动机为工具

这类题目与 AC 自动机的结构本身没有什么关系，不过需要以它为工具得出一些信息（如文本串 $S$ 的每个前缀所包含的最长模式串 $T$ ）。
- P7456 [CERC2018] The ABCD Murderer：数据结构优化 DP + AC 自动机。值得一提的是，这里的数据结构可以使用 反向 ST 表（在表一侧动态插入时维护区间最值）。
- P2292 [HNOI2004] L 语言：这可以被称为一道状压 DP。但不同的是，此处的状压并不是记录状态的工具，而是记录可行决策的工具——通过左移表示决策的相对变化，与取出决策，或加入决策。
拼凑文本串

这类题目会预先给定一堆模式串，然后让你在给定限制下拼凑出文本串。

这种问题一般是 DP 题。设状态时，我们往往需要将状态的第一维设为当前 AC 自动机的节点编号，代表一类文本串。
- P4052 [JSOI2007] 文本生成器：裸得不能再裸的 AC 自动机 + 计数 DP。
- P5319 [BJOI2019] 奥术神杖：AC 自动机上 DP + 取 $\log$ 的 01 分数规划。
- P3311 [SDOI2014] 数数：AC 自动机 + 数位 DP。
- P2444 [POI2000] 病毒：这道题目利用了 AC 自动机的结构将字符串问题转化为了图论问题。显然如果形成了一个环，就存在无限长的安全代码。
转化为树上问题

由于 fail 指针呈现树的结构，我们经常考虑将字符串包含问题转化为树上问题，然后用一些数据结构来维护。

一个特征是：文本串在 fail 树上所代表的那些点是随机分布在树中的。于是更具体地，我们可以认为这里的树上问题都是与随机点集相关的树上问题。
- P2414 [NOI2011] 阿狸的打字机：本题抽象出的结果可以看作“祖先路径查询”问题，而“祖先路径查询”和“子树查询”往往是可以互换的，在这里就是后者操作起来更为简单。
- P5840 [COCI2015] Divljak：本题中，我们通过对同种颜色的点建虚树来询问子树 $x$ 中有多少种颜色的点。
其它
- CF710F：动态 AC 自动机。见数据结构学习笔记 - 二进制分组。