你说得对,但 Splay 是最优美的平衡树!
本文主要介绍了 Splay 树的基本操作,以及相应的代码实现。有疑问请私信交流。
由于个人习惯,我会称“Splay 树”为“Splay”,“Splay 操作”为“伸展操作”或“splay”。
另外,为了表述方便,我将称“\(u\) 号点的父亲”为“\(\text{t[u].fa}\)”,称“\(u\) 号点的左儿子”为“\(\text{t[u].ls}\)”,称“\(u\) 号点的右儿子”为“\(\text{t[u].rs}\)”。
关于“平衡”
“平衡树”这个名称中的“平衡”二字,可以通过两个例子来理解。
现在我们有一棵树,记 \(n\) 为它的结点总数。当 \(n=5\) 时,如果它退化成了链,也就是下面这样:
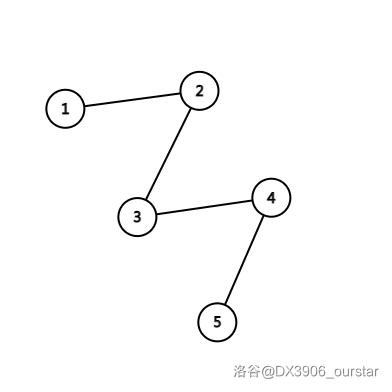
那么从根到叶子就需要经过 \(5\) 个结点,这也就意味着,它的复杂度是 \(O(n)\) 的。
但是,如果它是下面这样:
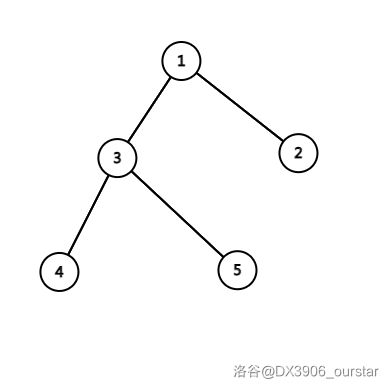
那么从根到叶最多只需要经过 \(3\) 个结点,也就是说,这个形态下,它的复杂度为 \(O(\log{n})\)。
一般地,我们认为前一幅图“不平衡”,而后一幅图是“平衡”的。也就是说,一棵树的结点分布越均匀,它就越“平衡”。
个人感觉 OI-wiki 写得太绕了,就像上面这样表述就挺好的。
而平衡树,顾名思义,就是维护一棵“平衡”的二叉搜索树。平衡树在“平衡”的同时又具有 BST(即二叉搜索树)的所有性质,因而可以在对数级复杂度内解决众多问题。
什么是 Splay?
怎么又是 Tarjan 老爷子的发明。
OI-wiki 云:
Splay 树,或 伸展树,是一种平衡二叉查找树,它通过 伸展(splay)操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 \(O(\log n)\) 时间内完成插入、查找和删除操作,并且保持平衡而不至于退化为链。
Splay 的基本操作
旋转
Splay 的灵魂,在于伸展;而伸展的灵魂,又在于旋转。
旋转,本质上就是在保持 BST 性质不变的同时,将某个结点上移一个位置,并将原有的父级结点作为自己的儿子。
Splay 定义了两种旋转操作:左旋和右旋。
这是 OI-wiki 上的示意图。
可能不太直观,我们以右旋为例,一起来分析一下。
这是某棵树本来的样子。
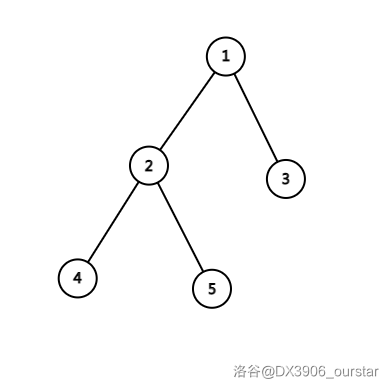
我们对 \(2\) 号点进行右旋。先把它拎出来,放在根的位置,让 \(1\) 号点变成它的儿子,像下面这样。

这时,我们注意到 \(2\) 号点有三个儿子了。这与 BST 的性质相悖,所以我们决定删去 \(2\) 号点和 \(5\) 号点之间的连线。于是 \(5\) 号点变成了 \(\text{t[1].ls}\),树就变成了下面这样:
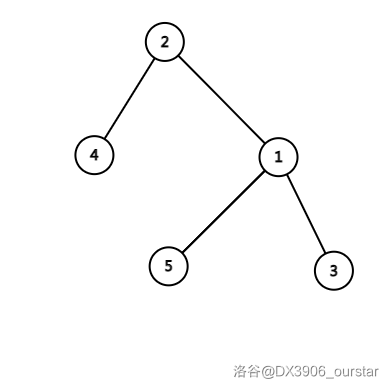
于是乎,右旋操作结束。容易发现,右旋前后,树的中序遍历不发生变化,BST 性质得以保持。
左旋类似于右旋,同理推导即可,这里不再赘述。关于它,@lcy6 云:
用一句话概括把左儿子转到自己位置的左旋:自己的左儿子改为左儿子的右儿子,左儿子的爹改为自己的爹,自己的爹认自己的左儿子,自己的爹改为左儿子。
附一个口诀:左旋拎右左挂右,右旋拎左右挂左。
为了保持树的平衡,我们常对左儿子进行右旋,对右儿子进行左旋。这就提供了一个机会,使得两种旋转可用同一函数实现。
伸展
旋转操作说完了,接下来看看伸展操作。
用人话表述这一操作:通过旋转,把某一结点弄到另一结点下方。
所以我们规定, splay(x,k) 为将 \(x\) 转到 \(k\) 下方;特别地,splay(x,0) 为将 \(x\) 转到根。上述规定有意义,当且仅当 \(k\) 是 \(x\) 的祖先。这不是废话吗。
接下来分别考虑 splay(x,k) 的几种情况。为了表述方便,我们记初始时 \(\text{t[x].fa}\) 为 \(y\),\(\text{t[t[x].fa].fa}\) 为 \(z\)。
说得通俗一点,就是记 \(x\) 的父亲为 \(y\),爷爷为 \(z\)。
1.\(y\) 即为 \(k\)
什么都不需要做。废话。
2.\(z\) 即为 \(k\)
只需旋转一次即可。具体地,如果 \(x\) 是 \(\text{t[y].ls}\),则右 \(x\);反之,左旋 \(x\)。
下面演示右旋 \(x\) 的情况。
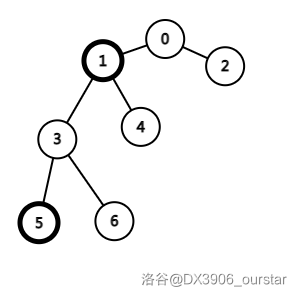
我们要执行 splay(5,1) 这一操作(两个节点均已加粗)。注意到 \(\text{t[3].ls}\) 是 \(5\) 号点,则应当对 \(5\) 号点进行右旋,变成下面这样:
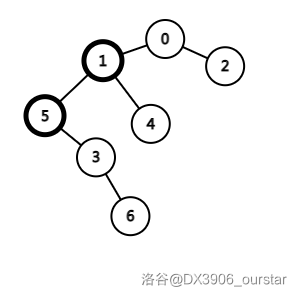
操作完成。
3.\(y\) 和 \(z\) 都不是 \(k\),且 \(x,y,z\) 共线。
那么,如果链 \(z\to y\to x\) 向左延伸,则先右旋 \(y\),再右旋 \(x\);反之,则先左旋 \(y\),再左旋 \(x\)。
“先旋转父亲,再旋转自己”的旋转方式称为双旋操作,双旋具有折叠效果,保证了每次操作的均摊复杂度为 \(O(\log n)\)。
以两次右旋为例。对于下面这张图:
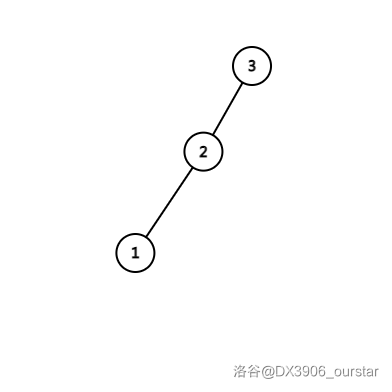
应当先右旋 \(2\) 号点,得到:
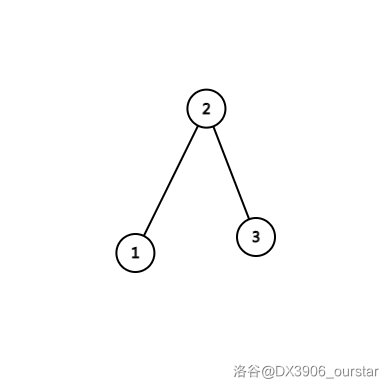
再右旋 \(1\) 号点,即:
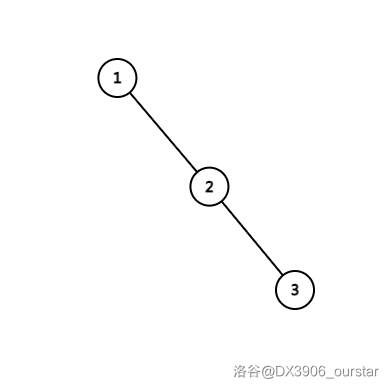
操作完成。
4.\(y\) 和 \(z\) 都不是 \(k\),且 \(x,y,z\) 呈“之”自形分布
转两次 \(x\) 即可。具体地,\(x\) 为 \(\text{t[t[x].fa].ls}\) 则右旋,反之则左旋。
还是演示一下。这是树本来的样子:
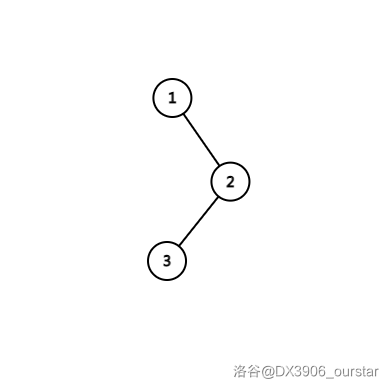
先右旋 \(3\) 号点,得:
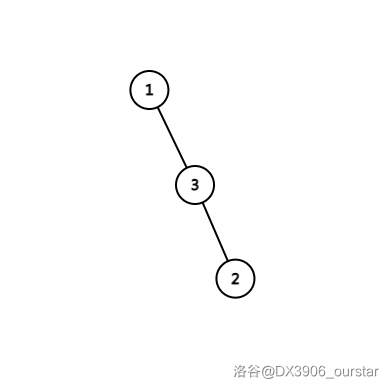
再左旋 \(3\) 号点,也就是:
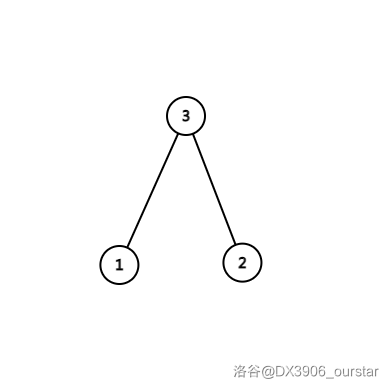
操作完成。
至此,分讨完毕,Splay 最基本的两种操作讲完了。
查找
记查找数字 \(v\) 对应的点号为 prepare(v)。这个操作的定义是,找到 \(v\) 在树中的位置,并将它旋转到根。
具体地,记当前所在结点为点 \(u\)。我们先令 \(u\) 为根,然后依照 BST 性质逐层向下寻找(\(v\) 大于 \(u\) 的权值就走右子树,否则走左子树),直到 \(u\) 的权值即为 \(v\) 或我们要走的子树为空时停止。最后 splay(u,0) 即可。
插入
用查找过程找到要插入的位置,进行插入。随后将新元素旋转到根。插入一段序列到 \(y\) 后,假设 \(y\) 的后继是 \(z\),我们会先将 \(y\) 旋转到根,然后再 splay(z,y)。此时只需将序列插入 \(z\) 的左子树即可。
删除
首先在树中找到要删除的元素 \(x\),将它转到根节点并删去,这样原来的树就分裂成了两棵树。接下来将左子树中拥有最大权值的那一个元素转到根,由于它是左子树中的最大元素,所以它不存在右儿子(BST 性质显然),这样只要把原来的右子树作为它的右子树,就重新合并成了一棵树。
查排名
通过查找操作把对应权值结点转到根,左子树大小加一即为所求(由 BST 性质可知,左子树内的所有结点的权都小于根)。
查找前驱、后继
首先将给定结点转到根,然后观察权值间的关系。以查找前驱为例。如果根的权值大于给定值,则此时的根即为答案;否则,继续向下查找。后继则可以同理,将判定条件变为“如果根的权值小于给定值”即可。
上述两个操作极为相似,因而可以在同一个函数内巧妙地实现。
第 \(k\) 小
可以根据左右子树的大小来判断。若 \(k\) 小于根的左子树大小(由 BST 性质,亦可理解为第 \(k\) 小的数比根的权值更小),则第 \(k\) 小的数一定在左子树;否则,在右子树。对于后一种情况,更新 \(k\),然后查找右子树中的第 \(k\) 小。上述过程重复进行,直到我们找到想要的结点。
可以想见,在右子树中查找时,\(k\) 应该减去对应的的左子树的大小。我们记左子树的大小为 \(x\),则我们要找的整棵树的第 \(k\) 小,实际上是右子树的第 \((k-x)\) 小。由 BST 性质可知,左子树的任意结点小于右子树的任意结点,因此,对于右子树,我们要把左子树的所有结点忽略掉。
同样由于 BST 性质,我们在查找左子树时无需考虑右子树,因为右子树的任意结点都更大,不可能挤进前 \(k\)小。
什么玩意,绕口令吗。
正确性证明
额,主播语文水平有限,说不太清楚,可以参考这篇博客。
代码实现
下面,我们以
P3369 【模板】普通平衡树为例,探讨 Splay 的代码实现。建议单开一个窗口,以便将代码和上面的描述相比对。
首先观察下面的 AC 代码,尝试理解它,再接着往后看。
#include<iostream>
#define INF 0x7fffffff
using namespace std;
int n;
namespace OIfast{
char buf[1<<21],*p1,*p2,*top, buffer[1<<21];
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?0:*p1++)
inline int read(){
register int n=0;
register short f=1;
register char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
n=(n<<1)+(n<<3)+(c^48);
c=getchar();
}
return n*(int)f;
}
inline void print(register int n){
register short sta[19];
register short top=0;
if(n<0)n=~n+1,putchar('-');
do{
sta[top++]=n%10;
n/=10;
}while(n);
while(top)putchar(sta[--top]^48);
return ;
}
inline void write(register int n,register char c){
print(n),putchar(c);
return ;
}
}using namespace OIfast;
namespace splayTree{
#define ls s[0]
#define rs s[1]
#define tmp(a) t[t[a].fa].rs==a
const int N=1e6+5;
int tot,root;
struct node{
int v,fa,size,cnt;
int s[2];
}t[N];
inline void init(int u,int _v,int _fa){
t[u].cnt=t[u].size=1;
t[u].v=_v,t[u].fa=_fa;
return ;
}
inline void pushup(int u){
t[u].size=t[t[u].ls].size+t[t[u].rs].size+t[u].cnt;
return ;
}
inline void rotate(int x){
int y=t[x].fa;
int z=t[y].fa;
bool k=tmp(x);
t[z].s[tmp(y)]=x,t[x].fa=z;
t[y].s[k]=t[x].s[k^1],t[t[x].s[k^1]].fa=y;
t[x].s[k^1]=y,t[y].fa=x;
pushup(y),pushup(x);
return ;
}
inline void splay(int x,int k){
while(t[x].fa!=k){
int y=t[x].fa;
int z=t[y].fa;
if(z!=k)rotate(((tmp(x))^(tmp(y)))?x:y);
rotate(x);
}
if(k==0)root=x;
return ;
}
inline void prepare(int v){
int u=root;
if(u==0)return ;
while(t[u].v!=v&&t[u].s[v>t[u].v]!=0){
u=t[u].s[v>t[u].v];
}
splay(u,0);
return ;
}
inline void add(int v){
int u=root,fa=0;
while(u!=0&&t[u].v!=v){
fa=u;
u=t[u].s[v>t[u].v];
}
if(u!=0){
++t[u].cnt;
}else{
u=++tot;
init(u,v,fa);
if(fa!=0){
t[fa].s[v>t[fa].v]=u;
}
}
splay(u,0);
return ;
}
inline int get(int v,bool f){
prepare(v);
int u=root;
if(v<t[u].v&&f)return u;
if(v>t[u].v&&(!f))return u;
u=t[u].s[f];
while(t[u].s[f^1]!=0){
u=t[u].s[f^1];
}
splay(u,0);
return u;
}
inline void del(int v){
int l=get(v,0),r=get(v,1);
splay(l,0),splay(r,l);
if(t[t[r].ls].cnt>1){
--t[t[r].ls].cnt;
splay(t[r].ls,0);
}else{
t[r].ls=0;
}
return ;
}
inline int rk(int v){
prepare(v);
return t[t[root].ls].size;
}
inline int kth(int k){
int u=root;
if(t[u].size<k)return -1;
while(1){
if(k>t[t[u].ls].size+t[u].cnt){
k-=t[t[u].ls].size+t[u].cnt;
u=t[u].rs;
}else{
if(t[t[u].ls].size>=k){
u=t[u].ls;
}else{
splay(u,0);
return t[u].v;
}
}
}
return 5201314;
}
}using namespace splayTree;
inline void work(){
int opt=read(),x=read();
if(1==2)puts("wow");
else if(opt==1)add(x);
else if(opt==2)del(x);
else if(opt==3)add(x),write(rk(x),'\n'),del(x);
else if(opt==4)write(kth(x+1),'\n');
else if(opt==5)write(t[get(x,0)].v,'\n');
else if(opt==6)write(t[get(x,1)].v,'\n');
return ;
}
signed main(){
add(-INF),add(INF);
n=read();
while(n--)work();
return 0;
}
接下来,我们将代码分成多个部分,分开讲解。
框架
#include<iostream>
#define INF 0x7fffffff//极大值
using namespace std;
int n;
namespace OIfast{//快读快写
char buf[1<<21],*p1,*p2,*top, buffer[1<<21];
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?0:*p1++)
inline int read(){
register int n=0;
register short f=1;
register char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
n=(n<<1)+(n<<3)+(c^48);
c=getchar();
}
return n*(int)f;
}
inline void print(register int n){
register short sta[19];
register short top=0;
if(n<0)n=~n+1,putchar('-');
do{
sta[top++]=n%10;
n/=10;
}while(n);
while(top)putchar(sta[--top]^48);
return ;
}
inline void write(register int n,register char c){
print(n),putchar(c);
return ;
}
}using namespace OIfast;
namespace splayTree{//平衡树相关代码
/*这部分代码略*/
}using namespace splayTree;
inline void work(){//处理单次操作
/*这部分代码略*/
return ;
}
signed main(){
add(-INF),add(INF);//插入哨兵
n=read();
while(n--)work();
return 0;
}
很好理解吧。由于个人习惯,我喜欢把功能相对独立的东西分开,封装在不同的命名空间里。其他部分 显然 应该是不需要解释的,重点放在主函数。
注意到主函数在进行其他操作前,先插入了一个最大值和最小值(称为 “哨兵”)。哨兵的存在,避免了 访问空子树 或 操作时没有有效结点 的情况,但同时,也会对其余部分的代码产生一系列影响。后面再来探讨这个问题。
基本定义
#define ls s[0]//便捷地表示左右儿子,一定程度上可以简化后面的代码。
#define rs s[1]
#define tmp(a) t[t[a].fa].rs==a//以后有用,先不管。
const int N=1e6+5;//结点数量上限。
int tot/*结点总数*/,root/*根*/;
struct node{
int v/*权值*/,fa/*父亲*/,size/*子树大小*/,cnt/*重复次数*/;
int s[2];//s[0] 表示左儿子,s[1] 表示右儿子。
}t[N];
可以发现,我们用一个数组来存储左右儿子。可能你会问:为什么不直接像线段树的结点定义一样,直接用 ls 和 rs 来表示左右儿子?
答案也很简单:之前的介绍中,我们提到了可以将两个相似的操作写在同一函数内。这些操作可能在面对同一条件时,一个会选择左儿子,另一个会选择右儿子;这时候,我们就可以 将这个条件(或对它进行某种运算的结果)直接作为下标,从而大大简化代码。
满满的都是前人的智慧啊,很巧妙吧?
init() 和 pushup()
inline void init(int u,int _v,int _fa){//创建节点后对它进行初始化。
t[u].cnt=t[u].size=1;
t[u].v=_v,t[u].fa=_fa;
return ;
}
inline void pushup(int u){//旋转后重新整合节点信息。
t[u].size=t[t[u].ls].size+t[t[u].rs].size+t[u].cnt;
return ;
}
都很好理解。容易发现,旋转后结点的左右子树可能发生变化,这时,之前的记录的子树大小就可能是错误的。因此,我们需要对它进行更新。左子树大小、右子树大小 和 结点本身的重复次数之和,即为以结点为根的子树的大小。
rotate()
inline void rotate(int x){
int y=t[x].fa;//和之前的介绍保持一致。
int z=t[y].fa;
bool k=tmp(x);//这就是那个宏定义的用处之一,可参照之前的介绍。
t[z].s[tmp(y)]=x,t[x].fa=z;
t[y].s[k]=t[x].s[k^1],t[t[x].s[k^1]].fa=y;
t[x].s[k^1]=y,t[y].fa=x;
pushup(y),pushup(x);
return ;
}
注意到调用时只需指定点号,并不需要考虑是左旋还是右旋,函数会自己决定。
可以看到,中间的三行就是旋转操作的核心。每行都可以认为是将前一个结点变成后一个结点的儿子,再把后一个结点变成前一个结点的父亲。
操作结束后,我们进行了两次 pushup 操作。仿照线段树,整合应当先下后上,所以我们先 pushup(y),后 pushup(x)。(旋转后 \(y\) 在 \(x\) 下方。)
splay()
inline void splay(int x,int k){
while(t[x].fa!=k){//只要还没有到 k 下方就不结束。
int y=t[x].fa;//如上。
int z=t[y].fa;
if(z!=k)rotate(((tmp(x))^(tmp(y)))?x:y);//三目运算符压了一下行,很合理吧。
rotate(x);
}
if(k==0)root=x;//如果是转到根的话,记得更新根的位置。
return ;
}
这个就没有太多可以讲的了,把之前的介绍写成代码即可。当然,你也可以写成这样:
inline void splay(int x,int k){
while(t[x].fa!=k){
int y=t[x].fa;
int z=t[y].fa;
if(z!=k){
if((t[y].rs==x)^(t[z].rs==y))rotate(x);//就是这里不一样。
else rotate(y);
}
rotate(x);
}
if(k==0)root=x;
return ;
}
这个版本易于理解、更贴近我们之前的描述,但显然码量更大。
prepare()
inline void prepare(int v){
int u=root;
if(u==0)return ;//此时 u 已经在 0 的位置了,不能继续操作。
while(t[u].v!=v&&t[u].s[v>t[u].v]!=0){//查找 u 的位置。
u=t[u].s[v>t[u].v];//向下找儿子。
}
splay(u,0);
return ;
}
我们从根开始,先特判一步,然后利用 BST 性质逐层向下寻找。找到之后转到根即可。
由 BST 性质可知,任意树节点的权值都大于左儿子且小于右儿子。因此,若给定权值大于当前结点的权值,则去找当前结点的右儿子;否则,找左儿子。再来观察表达式 v>t[u].v。在前一种情况下,它的值为 \(1\),而我们要找 t[u].s[1];后一种情况下,它的值为 \(0\),而我们要找 t[u].s[0]。
所以,我们可以 直接将这个表达式作为下标,向下寻找的过程,直接写作 u=t[u].s[v>t[u].v] 即可。
这一点非常有用,下面还会用到。
add()
inline void add(int v/*给定的数*/){
int u=root,fa=0;//初始时,u 为根,t[u].fa 自然就为 0。
while(u!=0&&t[u].v!=v){//向下找。
fa=u;//更新父亲。
u=t[u].s[v>t[u].v];//BST 性质。
}
if(u!=0){//这说明 v 已经在树中出现过。
++t[u].cnt;
}else{//新建结点。
u=++tot;
init(u,v,fa);//初始化。
if(fa!=0){//u 不在根的位置上。
t[fa].s[v>t[fa].v]=u;
}
}
splay(u,0);
return ;
}
对于要加入树中的一个数,我们需要考虑这个数是否在树中已经存在。若是,则仅需将对应结点的重复次数加上一;反之,新建一个结点。
新建结点包括更新点数(即 ++tot)、初始化结点信息(调用 init())两个基本步骤。另外还需判断新建的结点是否有父亲;若有,更新父亲的儿子信息;否则,什么都不用做。
另外,无论这个数是否已经存在,我们都应将其对应的结点转到根。别问为什么,问就是 Splay 就是这样写的,不加上会 WA。
get()
inline int get(int v,bool f/*为 0 表示找前驱,为 1 表示找后继。*/){
prepare(v);
int u=root;
if(v<t[u].v&&f)return u;//找后继时,根的权值大于给定值。
if(v>t[u].v&&(!f))return u;//找前驱时,根的权值小于给定值。
u=t[u].s[f];//准备跳。
while(t[u].s[f^1]!=0){//此时 u 还有儿子,往下跳。
u=t[u].s[f^1];
}
splay(u,0);//同样,这一句也是不能去掉的。
return u;
}
这个也没有太多要讲的东西,把之前讲的直接实现即可。
注意跳之前的两个特判,它们分别对应了查找两种东西时根即为答案的情况。
del()
inline void del(int v){
int l=get(v,0),r=get(v,1);//查找前驱后缀时就已经转到根了,无需单独 splay。
splay(l,0),splay(r,l);//将前驱转到根,将后继转到前驱下方。
if(t[t[r].ls].cnt>1){//有重复,减去重复次数即可。
--t[t[r].ls].cnt;
splay(t[r].ls,0);
}else{
t[r].ls=0;//删除左儿子。
}
return ;
}
和之前的叙述保持一致。可能比较难想,但我觉得我已经尽力说清楚了。实在不行就把这段代码背下来吧。
rk()
inline int rk(int v){
prepare(v);//转到根。
return t[t[root].ls].size;//左子树大小。
}
这是全场最简单的操作力!
需要注意的是,按照我们之前的讲述,排名应为左子树大小加一。但由于哨兵的影响,左子树中还会有一个极小值,它让子树大小增加了一。因此直接返回 t[t[root].ls].size 即可。
kth()
inline int kth(int k){
int u=root;
if(t[u].size<k)return -1;//整棵树都没有 k 个结点,无解。
while(1){
if(k>t[t[u].ls].size+t[u].cnt){//k 大于左子树大小,答案必然在右子树。
k-=t[t[u].ls].size+t[u].cnt;//更新 k,如上所述。
u=t[u].rs;
}else{
if(t[t[u].ls].size>=k){//k 不大于左子树大小,答案在左子树。
u=t[u].ls;
}else{//答案不在左子树也不在右子树,必然就是当前结点。
splay(u,0);//可以不写,但那样更慢。
return t[u].v;
}
}
}
return 5201314;//美观起见,我在每个函数后面都写了返回语句。但程序不可能来到这里,所以就随便安了个返回值。
}
好像也没什么可讲的。 关于找到答案之后的 splay(u,0),虽不是必需品,但体现了 Splay 特有的“缓存”机制,即将访问过的点尽可能靠近根,以提升整体的运行速度。
work()
inline void work(){
int opt=read(),x=read();
if(1==2)puts("wow");//还是为了美观,随便加个 if 可以让所有操作前都是 else if。
else if(opt==1)add(x);
else if(opt==2)del(x);
else if(opt==3)add(x),write(rk(x),'\n'),del(x);
else if(opt==4)write(kth(x+1),'\n');
else if(opt==5)write(t[get(x,0)].v,'\n');
else if(opt==6)write(t[get(x,1)].v,'\n');
return ;
}
直接按题意书写即可。需要注意的是,对于操作 \(3\),\(x\) 不一定存在,需要先插入 \(x\) 以保证不出错,再删除 \(x\) 以避免后续影响;对于操作 \(4\),考虑哨兵影响,存在极小值的第 \(k\) 小实际上是第 \((k+1)\) 小;对于操作 \(5\) 和操作 \(6\),我们是直接用权值进行查找的,因此无需先加入后删除。
代码部分就结束力!
说句闲话——选排优于快排,梦境还是现实?
前几天数学在讲第二十章,我感觉把那堆弱智问题放到 OI 里会有意思得多……
我注意到在求中位数时,laoshi 对数列进行了排序,其手法大约等价于选排(即先找出原序列最小值,拿到新序列里,再把它扔出原序列,重复这一步骤直到原序列中没有剩余元素,排序结果即为新序列)。
同学们都知道,这一操作是 \(O(n^ 2 )\) 的,慢得令人发指。于是闲的没事的我昨晚做了个梦,梦里,我口胡出了用平衡树优化区间最小值的操作。
具体地,维护一棵 Splay 树,将原序列的所有数加入进去;然后不断执行第 \(k\) 小操作并删除找到的数。这样,整个排序过程就优化到了 \(O(n \log n)\)——加入元素是 \(O(n)\) 的,查找第 \(k\) 小是 \(O(\log n)\) 的。
这就意味着,这样操作之后的选排具有跟快排同等的复杂度,应该能够通过 P1177 【模板】排序!
后来试了一下,你别说,还真行。横向对比一下,甚至优于快排、归并和堆排!
当然,也可以通过不断查找后继来实现,但缺陷在于需要想办法记录每个数出现的次数。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号