洛谷P2241 统计方形 ，棋盘问题升级板，给出格子坐标中矩形以及正方形的计算方法

在做这道题之前我们先了解一下棋盘问题

棋盘问题 (qq.com)

对于棋盘问题，我们可以得出对于一个n*n的正方形方格阵如何求其包含的正方形个数

      也就是数每个正方形的中间点，然后将其点排列成矩阵，对于其中m*m规格的正方形，其个数为(n-m-1)*(n-m-1)-

现在回到我们这道题，他的要求就更普适化，要在一般的矩形里来分别找正方形以及不包括正方形的矩形。但是对于一个m*n的矩形，其包含的k*k规格的正方形，仍然满足上述规律

也就是说对于k*k的正方形，其个数为(m-k-1)(n-k-1)

给出一个例子

这是一个4*5的矩形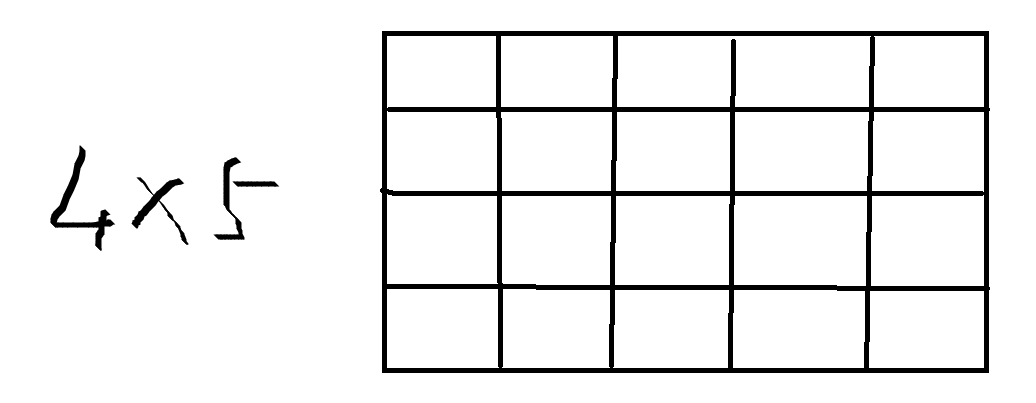

 对于其中2*2的正方形,我们仍旧可以仿照上述来找中心点来计数，如下

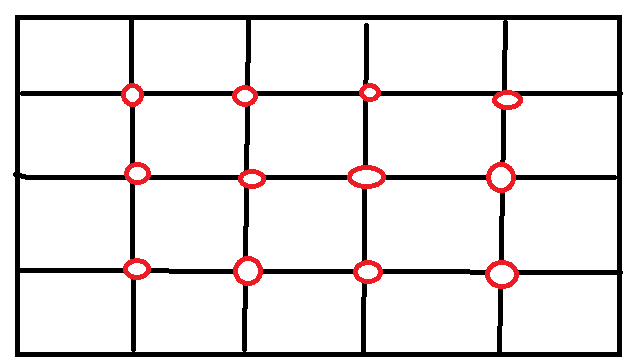可以看出由于2*2的矩形的边界效应，也就是其边界上的正方形区域所以其中心点矩阵正好是3*4，也就是4*5减去占用边界的1格

同理对于3*3正方形

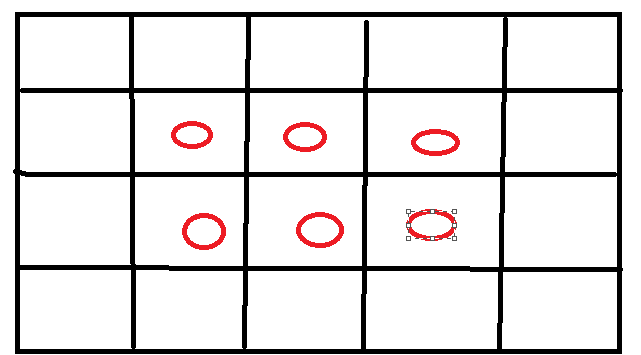可以看出其中心矩阵为2*3，也就是4*5减去占用边界的1.5格(取整即为2)4-2=2，5-2=3，即向内缩进一圈

由此可以知道计算纯正方形个数的规律对于一个m*n的矩阵其中k*k正方形个数为(m-k-1)(n-k-1),但是其中最大的正方形边长为min(m,n)

计算完正方形，对于一个m*n的矩形，我们想办法求出其矩形(包含正方形)的个数

 

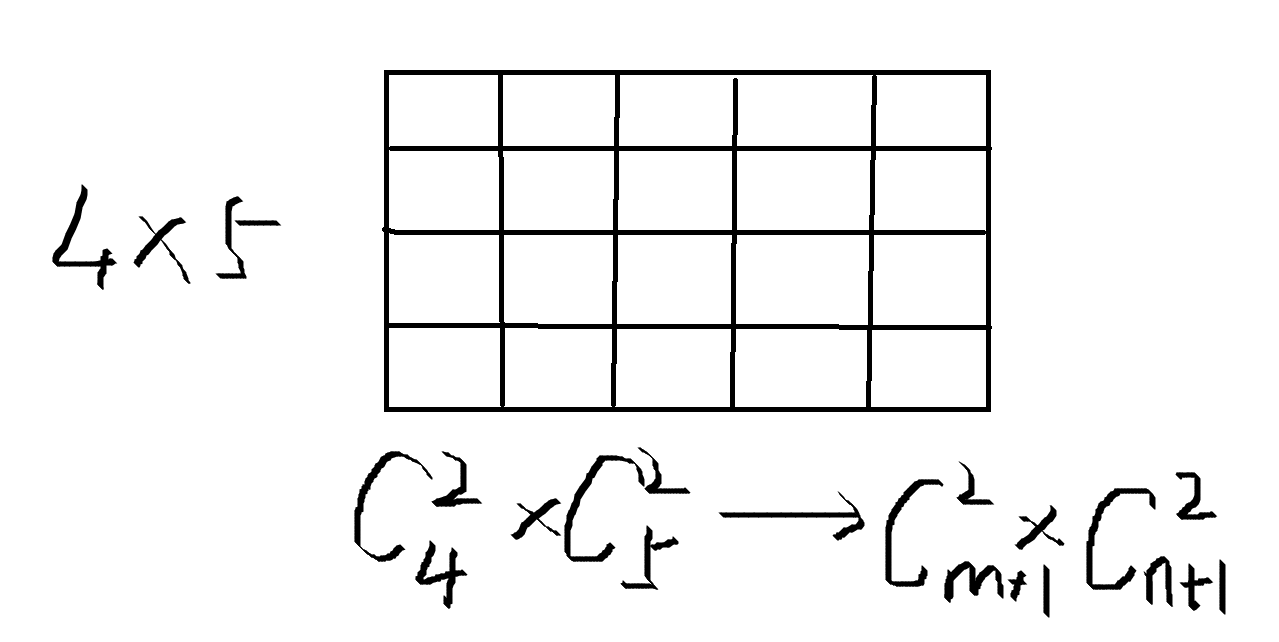
 由小学高中学过的排列组合可知道，一个矩形由两条竖边和两条横边组成，因此只需要在方格图中任选两条竖边和任选两条横边并组合起来就可以得到矩形的个数

这样一来我们就求出了正方形的个数和矩形的个数，因此不包含正方形的矩形的个数就是       所有矩形的个数-正方形的个数

思路解决，下附上AC代码

    cin >> n >> m;
    long long NumOfC = 0;//所有矩形个数
    long long N = 1, M = 1;
    for (int k = 0; k<2; k++)
    {
        N *= (n+1 - k); M *= (m+1 - k);
    }
    NumOfC = (N / 2) * (M / 2);//求出所有矩形个数
    int i = n; int j = m;
    long long NumOfS = 0;//正方形个数
    while (i >= 0 && j >= 0)
    {
        NumOfS += (i--) * (j--);//求出正方形个数，从m*n开始一直求到一方为0结束
    }
    cout << NumOfS << ' ' << NumOfC - NumOfS;//输出
}