CF559E Gerald and Path

有 \(n\) 条线段，每条线段给定其中一端的位置及长度，求所有线段覆盖的最大长度。\(n \leq 100\)。

看看我之前写的都是啥：

首先对线段以左端点为关键字升序排序。
设 \(dp_{i,j,0/1}\) 表示前 \(i\) 条线段，最靠右的线段编号为 \(j (j \lt i)\)，它的朝向是左或右。
考虑转移，枚举 \(i\) 后面线段的方向，由于选择的线段是一个前缀，所以要记录前缀最右线段的端点、长度、朝向等信息并转移。

这题解写得有点太好了。

---

自然地想到先对端点排序，从左往右覆盖。设 \(f_{i,j,0/1}\) 表示前 \(i\) 个线段已经被定向，右端点最靠右的线段编号为 \(j\)，它的朝向是左还是右。
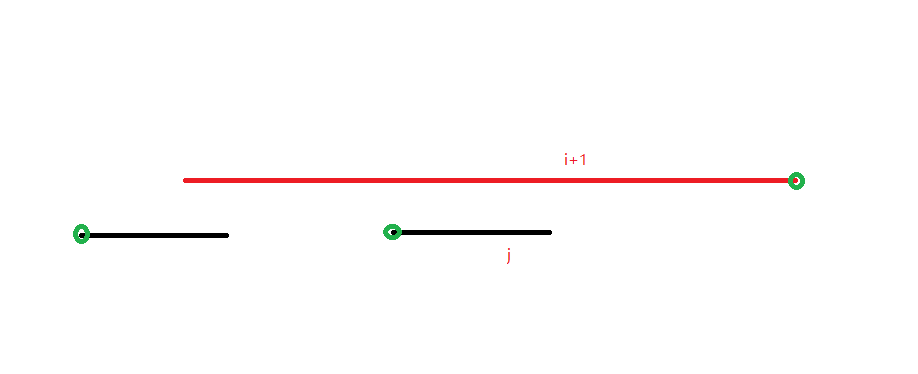
如果直接做的话会出现后效性，如下图：

转移枚举 \(i+1\) 的方向，算出右端点 \(a\)，设 \(j\) 的右端点为 \(b\)，\(i+1\) 的长度为 \(l\)，那么贡献就是 \(\min(l, a-b)\)。
显然这样线段 \(j\) 左边那一小块空白没被算进去。

---

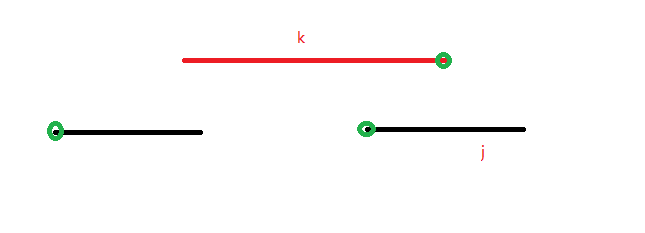
这启发我们直接去枚举下一个产生贡献的线段 \(k \in [i+1,n]\)，而忽略 \([i+1,k-1]\) 线段的贡献。
虽然这明显不优，但这样显然可以考虑到最优情况，除了下面这种特例：

\([i+1,k-1]\) 的右端点最靠右线段 \(j\) 超过了 \(k\) 右端点，那么超出的部分也应当计算。
显然由于排序后 \(j \lt k\)，所以 \(k\) 右端点到 \(j\) 右端点这段超出部分一定是被连续覆盖的，这种情况只会在 \(k\) 往左的时候出现。

#include <bits/stdc++.h>
using namespace std;
const int N = 115;
int n, dp[N][N][N];
pair<int, int> a[N];
int ans = 0;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].first, &a[i].second);
    sort(a + 1, a + 1 + n);
    a[0].first = -0x3f3f3f3f;
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= i; j++) {
            for (int fx = 0; fx <= 1; fx++) {
                ans = max(ans, dp[i][j][fx]);
                int o = (fx == 0) ? a[j].first : a[j].first + a[j].second, x = 0, y = -1, z = -0x3f3f3f3f;
                for (int k = i + 1; k <= n; k++) {
                    for (int fx2 = 0; fx2 <= 1; fx2++) {
                        int t = (fx2 == 0) ? a[k].first : a[k].first + a[k].second, q = fx2;
                        if (t > z) x = k, y = q, z = t;
                        dp[k][x][y] = max(dp[k][x][y], dp[i][j][fx] + min(a[k].second, t - o) + z - t);
                    }
                }
            }
        }
    printf("%d\n", ans);
    return 0;
}