数学总结 7(浅谈计算几何)
一、基础概念
点积
设 \(A(x_1,y_1), B(x_2,y_2)\),定义点积运算:
根据定义 2:
- 当 \(\theta = 0\),有 \(\vec{OA} \cdot \vec{OB} = |OA| \times |OB|\)。
- 当 \(\theta = 90\),有 \(\vec{OA} \cdot \vec{OB} = 0\)。
- 当 \(\theta \in (0,90)\),有 \(\vec{OA} \cdot \vec{OB} \gt 0\)。
- 当 \(\theta \in (90,180)\),有 \(\vec{OA} \cdot \vec{OB} \lt 0\)。
一般可以用来判定垂直、判定锐角或钝角。
叉积
其中 \(\theta\) 为有向角。
由于是有向角,交换律需要变号:
叉积可以用来判定方向。
具体地,若 \(\vec{OB}\) 在 \(\vec{OA}\) 的逆时针方向,叉积为正;否则为负。
叉积还可以算面积。
叉积算的其实就是 \(\vec{OA}, \vec{OB}\) 围成的平行四边形面积,注意这也是有向面积。
简单题
判断点在直线哪一侧
直接叉积看结果正负性。
- \(\gt 0\) 则在逆时针方向。
- \(=0\) 在直线上
- \(\lt 0\) 在顺时针方向。
判断点是否在线段上
先判断它是否在直线上,用叉积。
然后判断 \(x \in [\min(x_1, x_2), \max(x_1, x_2)], y \in [\min(y_1, y_2), \max(y_1, y_2)]\)。
求直线的解析式
这很简单吧,已知过 \((x_1, y_1), (x_2, y_2)\),列个方程就行了。
注意特判 \(k = \infty\) 的情况。
求两条直线的交点
先求解析式,再暴力联立直接算。
同样需要注意特判 \(k = \infty\) 的情况。
例 1:极角排序
极角取值范围一般定为 \((-\pi, \pi]\),指的是 \(\vec{OA}\) 和 \(x\) 轴正半轴成的角度,\(x\) 负半轴上定义为 \(-\pi\),同理 \(y\) 正半轴定义为 \(\frac{\pi}{2}\) 以此类推。
代码可以直接用 atan2(y, x) 算出 \((x,y)\) 的极角,long double 的话用 atan2l(y, x),注意先 \(y\) 后 \(x\)。
直接用 atan2 排会有精度误差,而且三角函数跑得慢。
考虑用叉积判方向,但是直接判可能会有环,例如三个向量两两之间成 \(120\) 度……
可以先“分界”之后再判定。具体地,将 \(x\) 轴以上的拉出来 sort,以下的拉出来 sort,再拼在一起即可。
当然,有另一种更直观的写法:按照坐标轴、四象限分成八个区域,先按区域排,区域内部按斜率排,代码在后文。
#include <bits/stdc++.h>
#define PII pair<int, int>
#define x first
#define y second
using namespace std;
const int N = 2e5 + 5;
int t, n, m;
PII a[N], b[N];
bool cmp(PII a, PII b) { // 叉积
long long opt = a.x * 1ll * b.y - b.x * 1ll * a.y;
if (opt == 0) return abs(a.x) < abs(b.x);
return (opt > 0);
}
int main() {
scanf("%d", &t);
for (int i = 1, x, y; i <= t; i++) {
scanf("%d%d", &x, &y);
if (y > 0 || (y == 0 && x <= 0)) a[++n] = {x, y};
else b[++m] = {x, y};
}
sort(a + 1, a + 1 + n, cmp);
sort(b + 1, b + 1 + m, cmp);
for (int i = 1; i <= m; i++) printf("%d %d\n", b[i].x, b[i].y);
for (int i = 1; i <= n; i++) printf("%d %d\n", a[i].x, a[i].y);
return 0;
}
例 2:洛谷 P3476 [POI 2008] TRO-Triangles
要求所有三角形的面积之和……
看上去很吓人,先干一个海伦公式上去 \(O(n^3)\)。
令 \(p=\frac{a+b+c}{2}\),则 \(S = \sqrt{p(p-a)(p-b)(p-c)}\)。
然后考虑先确定三角形中的一个点。
不妨把三角形面积的贡献挂在这样的一个点上:它 \((-\pi, \pi]\) 的角度范围内可以覆盖另外两个点。
然后我们只需要枚举每个点,将符合这个条件的点拎出来做极角排序……然后 \(S = \frac{1}{2} |x_1y_2 - x_2y_1|\)。
绝对值很烦,但只要按极角从大到小枚举点这个式子就是正的,计算一下 \(\sum x, \sum y\) 就可以分配律求了。
时间复杂度 \(O(n^2 \log n)\),瓶颈在排序。
例 3:求多边形面积
给定 \(n\) 个点组成的凸多边形,求面积。
显然可以在凸多边形内部任选一点 \(O\),然后将凸多边形分为 \(n\) 个三角形求面积和。
三角形面积叉积一下就可以了。
然后考虑如何选这个点 \(O\),事实上只要是在这个平面内的点都可以选。
因为计算出来的面积是有向的,在凸多边形外部的会被反向抵消掉,手模发现是对的。
求简单多边形面积:边不交,但不一定是凸多边形。
类似地,也可以用上面的方法做,即多边形外的面积被抵消。
二、凸包
给定 \(n\) 个点,找一个面积最小的多边形覆盖所有点,多边形称为凸包。
还有斜率逼近法、Jarvis 算法和 Graham 算法。
这里只记一下比较好写的 Andrew 算法了(虽然 Graham 也不错?)。
- 先把点按双关键字排序。
- 然后按顺序加入点,用单调栈维护凸包的“凸性”
- 具体地,如果加入这个点之后“转向”了,那么就弹出栈顶继续判定,重复直到栈中只有一个点或符合条件,就把这个点扔进去。
- 但这样只能求出一个下凸壳……假设现在栈顶的点是 \(P\)。
- 如何求出完整的凸包?反着枚举点的顺序,从 \(P\) 开始继续求一个上凸壳即可。
例 4:洛谷 P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
如题,是板子。
#include <bits/stdc++.h>
#define PII pair<double, double>
#define x first
#define y second
using namespace std;
const int N = 2e5 + 5;
int n, tot;
PII a[N];
inline double cha(PII a, PII b) { return a.x * b.y - b.x * a.y; }
inline bool chk(PII a, PII b, PII c) {
b.x -= a.x, b.y -= a.y, c.x -= a.x, c.y -= a.y;
return cha(c, b) > 0;
}
PII stk[N]; int top;
void solve() {
top = 2, stk[1] = a[1], stk[2] = a[2];
for (int i = 3; i <= n; i++) {
while (top >= 2 && chk(stk[top - 1], stk[top], a[i])) top--;
stk[++top] = a[i];
}
int tt = top;
stk[++top] = a[n - 1];
for (int i = n - 2; i >= 1; i--) {
while (top > tt && chk(stk[top - 1], stk[top], a[i])) top--;
stk[++top] = a[i];
}
// for (int i = 1; i <= top; i++) cout << stk[i].x << ' ' << stk[i].y << endl;
}
inline double dis(PII a, PII b) { return sqrt((b.x - a.x) * (b.x - a.x) + (b.y - a.y) * (b.y - a.y)); }
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%lf%lf", &a[i].x, &a[i].y);
if (n == 1) return puts("0.00"), 0;
sort(a + 1, a + 1 + n);
solve();
double ans = 0;
for (int i = 1; i < top; i++) ans += dis(stk[i], stk[i + 1]);
printf("%.2lf\n", ans);
return 0;
}
例 5:洛谷 P3829 [SHOI2012] 信用卡凸包
直接把算法写在题目里了……
不难发现圆弧部分其实就是一整个圆的周长,所以只需要计算去掉圆半径之后的凸包周长即可。
那么只要求出四个点,这是好做的,长宽乘个三角函数再偏移到中心点即可。
于是求一下凸包周长再加上圆周长就是答案。
例 6:判断点是否在凸包内
给定一个凸包,多次询问判断 \((x, y)\) 是否在凸包内,\(n, q \leq 10^5\)。
暴力遍历凸包每条边,看这个点是否都在它的逆时针方向(叉积),\(O(nq)\)。
这个想法很笨……因为我们多判断了很多无用边,没有利用凸包的单调性。
可以在凸包上二分,先将 \(1\) 号点和其它每一个点连线,相邻两条线和凸包的边会构成若干三角形,二分点在哪个三角形内,查询它是否在对边的逆时针方向即可,总复杂度 \(O(q \log n)\)。
\(1\) 号点左右的边可能得特判一下边界以外,但这是细节。
代码在后文【战争】这道题。
例 7:洛谷 P4049 [JSOI2007] 合金
多么搞笑的题目啊。……
Corner Case 一大堆,卡了两个小时。
比较 tricky,但首先由于 \(a+b+c=1\),只需要知道 \((a,b)\) 就能确定唯一的 \(c\),不妨把一个材料或合金看作 \((a,b)\) 这一个二维平面上的点。
然后考虑“合成”这件事,如果要选出一些 \(A\) 集合中的点合成 \(B\) 集合中的一个点 \(P\),则这些点围成的凸包要包含 \(P\) 点。
显然,凸包内的点可以任意取,所以只要保证 \(P\) 在内即可。
为什么“显然”?
考虑从 \(p\) 点向凸包上所有点连边,形成若干个向量。
这些向量通过分配 \([0,1]\) 权值数乘、相加只能构成凸包内的点集。
类似于线性基。
或者……一个看起来更对的证明是:
考虑 \(x\) 坐标最大和最小限制了 \(x\) 的上下界,\(y\) 坐标同理。
上下界可以刻画成两条直线,夹着这个凸包。
所以对这个凸包做旋转卡壳(在后文有讲解)一直在两条直线间的就是可以拼出的部分。
显然,这些部分就是凸包本身。
然后就是从 \(A\) 中取最少的点包含 \(B\) 中所有点。
最开始的思路是对于 \(A\) 中 \((x,y)\) 点对,只要 \(B\) 中所有点都在直线 \((x,y)\) 的同一侧即可。
但是会出现虽然围成了凸包,依然无法包含所有点的情况。
所以考虑钦定一个方向:例如所有点都在直线的逆时针方向,叉积为正。
并且还要保证如果叉积为零,点必须在线段上才能覆盖。
然后 \((x,y)\) 就可以选择,否则不能选择。
接下来是选取最少的 \((x,y)\) 并构成一个凸包,建立图论模型就是形成环。
类似于 Floyd 求无向图最小环,这题求有向图最小环即可。
动态凸包
大致是拿平衡树找到插入的位置,然后向左向右暴力扔出在凸包内的点。
由于每个点只会进一次出一次,复杂度是 \(O(n \log n)\)。
三、旋转卡壳
给定平面上 \(n\) 个点,求最远的两个点之间的距离以及这两个点。
首先贪心,显然地我们只需要在凸包上决策选哪两个点即可。
然后事情交给旋转卡壳去做。
顾名思义,就是用两根直线恰好卡在凸包的两侧,和凸包的边不交(可以重合),然后旋转凸包调整直径。这个过程中两条直线之间距离最大值就是凸包的直径。
对踵点:显然这两条直线会卡在凸包的两个点上,此时称这两个点为一组对踵点对。
在凸包旋转的过程中,当对踵点对连线与直线垂直,两直线间的距离就是这两个点的距离,否则小于这两个点的距离(显然)
所以直线之间的距离一定能取到对踵点对距离:
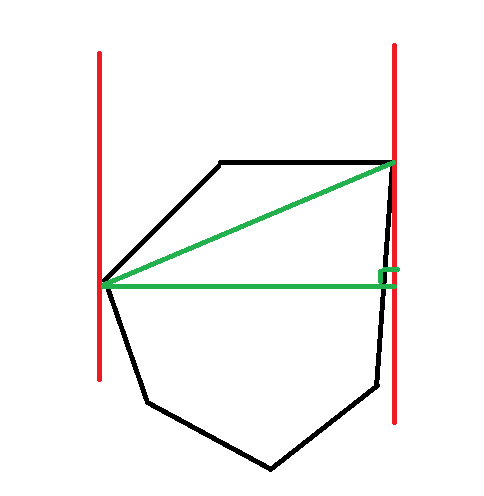
另外观察凸包“旋转”的过程,什么时候对踵点会发生改变?
当其中一条直线和凸包的某条边重合,就是另一组对踵点对的开始。
如下图,\(\color{blue}{蓝色}\)直线顺时针旋转得到新的\(\color{red}{红色}\)直线,产生了\(\color{green}{绿色}\)新的对踵点对。
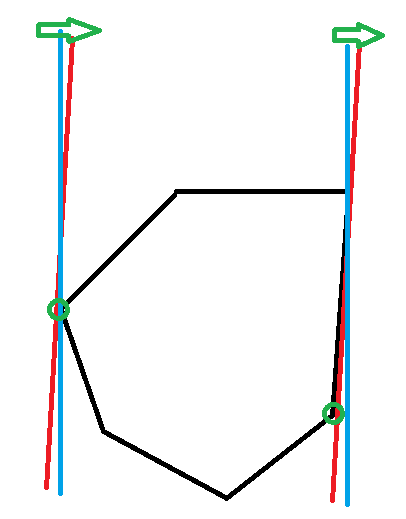
而且在旋转过程中,两个对踵点都是单调顺时针转或都单调逆时针转,取决于旋转方向(这个也很显然)。
这启发我们先任选一组对踵点对,然后朝着固定方向旋转直到其中一条直线与凸包的边重合,然后更新对踵点对距离作为凸包直径。
这个过程很麻烦……旋转直线?听起来很不可做,但是我们不妨枚举重合的边,由于另一个对踵点满足单调性,可以用双指针维护。
现在的问题是移动另一个对踵点。转化为如何比较两个点中哪一个到这条边的距离更大?
看到距离,作垂线。由于这条边的长度是确定的,所以围成三角形面积确定(可以用叉积算出),已知底边和面积求高,小学数学秒了。
例 8:洛谷 P1452 【模板】旋转卡壳 | [USACO03FALL] Beauty Contest G
int n;
struct Point { int x, y, id; } p[N];
inline long long cha(Point a, Point b) { return a.x * 1ll * b.y - b.x * 1ll * a.y; } // 叉积
inline long long S(Point a, Point b, Point c) { b.x -= a.x, b.y -= a.y, c.x -= a.x, c.y -= a.y; return cha(b, c); } // 三角形面积(有向)
inline long long dist(Point a, Point b) { return (a.x - b.x) * 1ll * (a.x - b.x) + (a.y - b.y) * 1ll * (a.y - b.y); } //距离平方
Point stk[N]; int top;
void Convex(); // 凸包,top 个点存在 stk 里
long long ans; int px, py;
inline void update(Point x, Point y) {
register long long res = dist(x, y);
if (ans < res) ans = res, px = x.id, py = y.id;
}
void rotating() {
if (top <= 2) { if (top == 2) update(stk[1], stk[2]); return; }
int now = 2; //当前对面的“对踵点”
for (int i = 1; i <= top; i++) {
while (llabs(S(stk[i], stk[i + 1], stk[now % top + 1])) > llabs(S(stk[i], stk[i + 1], stk[now]))) now = now % top + 1;
update(stk[i], stk[now]), update(stk[i + 1], stk[now]);
}
}
四、半平面交
半平面:给定一条有向直线 \(l\),\(l\) 左侧的所有点构成点集就称作一个半平面。
半平面交:给定 \(n\) 条有向直线,它们半平面的交集就是半平面交。
拿一张 OI-Wiki 的图:
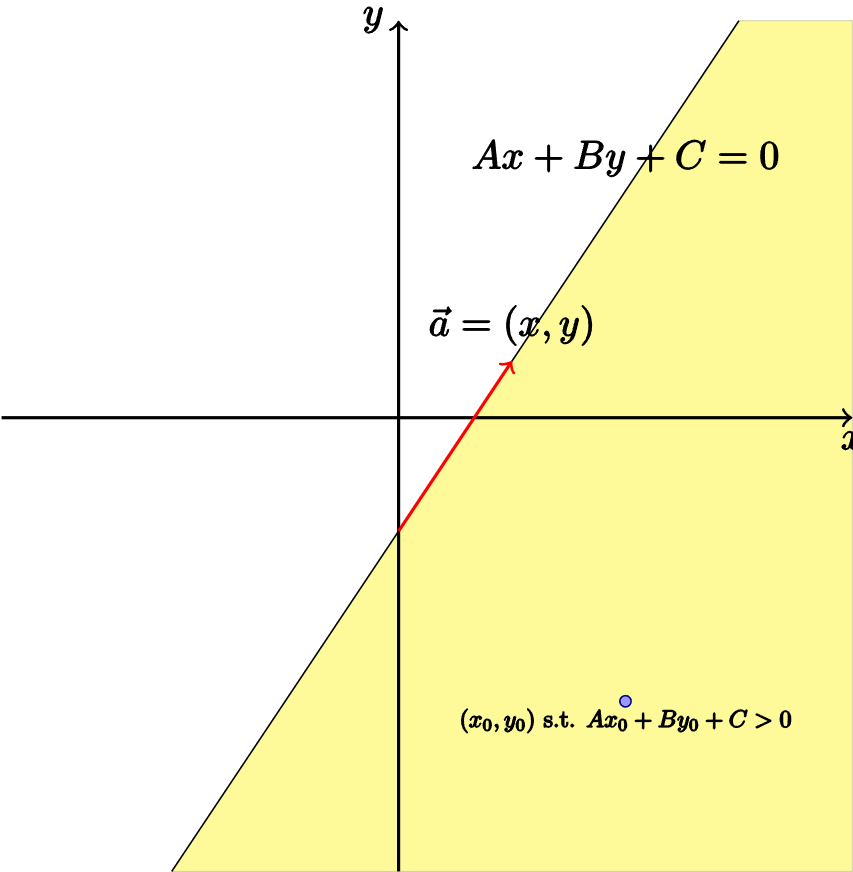
如图就是一个半平面交:
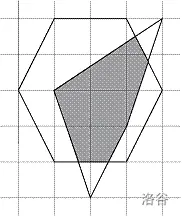
求解半平面交一般使用 S&I 算法,算法核心是单调栈。
- 先对所有有向直线做极角排序。
- 由于规定了半平面是左侧平面,所以对于极角相同的直线只保留靠左的。
- 按顺序往栈中加入直线,每次检查栈顶两条直线和待加入直线的关系。
- 设待加入直线为 \(l\),栈顶两条直线为 \(u,v\),栈顶两条直线交点为 \(O\)。
- 若 \(O\) 在 \(l\) 的右侧或在 \(l\) 上,则弹出栈顶,继续判定。
- 绕一圈回来再检查栈顶、栈底是否满足条件。
- 若栈顶两条直线的交点不在栈底直线的左边,弹出栈顶。
- 若栈底两条直线的交点不在栈顶直线的左边,删除栈底。
- 最后栈内直线围成的就是半平面交。
极角相同直线保留最左边,可以用叉积完成。
例 9:洛谷 P4196 [CQOI2006] 凸多边形 /【模板】半平面交
极角排序部分为了看起来更加赏心悦目,写了第二种方法(分八块按斜率排序)。
另外这题数据范围较小,所以不卡精度。
没看题解自己胡的代码,所以比较丑……
#include <bits/stdc++.h>
using namespace std;
const int N = 505;
struct Point { double x, y; int id; } ;
struct Line {
Point a, b;
double k, c;
int id;
inline void get() {
if (a.x == b.x) k = 1e9, c = 0;
else {
k = (a.y - b.y) / (a.x - b.x);
c = a.y - k * a.x;
}
}
} ; // (a, b); y = kx + c
int n, m, t1, t2;
Point p[N];
Line seg[N], seg2[N], l[N];
inline double cha(Point a, Point b) { return a.x * b.y - b.x * a.y; }
inline int pos(Point a) {
if (a.x > 0 && a.y == 0) return 1;
if (a.x > 0 && a.y > 0) return 2;
if (a.x == 0 && a.y > 0) return 3;
if (a.x < 0 && a.y > 0) return 4;
if (a.x < 0 && a.y == 0) return 5;
if (a.x < 0 && a.y < 0) return 6;
if (a.x == 0 && a.y < 0) return 7;
return 8;
}
inline bool cmp(Point a, Point b) {
int pa = pos(a), pb = pos(b);
if (pa ^ pb) return pa < pb;
return a.y * b.x < b.y * a.x;
}
inline Point met(Line a, Line b) {
if (a.k > b.k) swap(a, b);
if (b.k == 1e9) return (Point){b.a.x, a.k * b.a.x + a.c, 0};
double x = (b.c - a.c) / (a.k - b.k);
double y = a.k * x + a.c;
return (Point){x, y, 0};
}
bool check(Point a, Point b, Point c) { // c 是否在直线 ab 的逆时针方向
b.x -= a.x, b.y -= a.y, c.x -= a.x, c.y -= a.y;
return cha(b, c) > 0;
}
Line stk[N]; int top = 0;
Point ans[N]; int cnt;
int main() {
scanf("%d", &t1);
for (int i = 1; i <= t1; i++) {
scanf("%d", &t2);
for (int j = 1; j <= t2; j++) scanf("%lf%lf", &p[j].x, &p[j].y);
for (int j = 1; j <= t2; j++) seg[++n] = {p[j], p[j % t2 + 1]}, seg[n].get(), seg[n].id = n;
}
for (int i = 1; i <= n; i++) p[i] = {seg[i].b.x - seg[i].a.x, seg[i].b.y - seg[i].a.y, i};
sort(p + 1, p + 1 + n, cmp); // 极角排序
for (int i = 1; i <= n; i++) seg2[i] = seg[p[i].id];
// for (int i = 1; i <= n; i++) cout << '\t' << seg2[i].a.x << ' ' << seg2[i].a.y << '\t' << seg2[i].b.x << ' ' << seg2[i].b.y << endl;
for (int i = 1, j; i <= n; i = j + 1) {
j = i;
while (j < n && cha(p[j], p[j + 1]) == 0) j++; // 极角相同
Line Min = seg2[i];
for (int k = i + 1; k <= j; k++) {
if (check(Min.a, Min.b, seg2[k].a)) Min = seg2[k];
}
l[++m] = Min;
}
// for (int i = 1; i <= m; i++) cout << l[i].a.x << ' ' << l[i].a.y << '\t' << l[i].b.x << ' ' << l[i].b.y << endl;
for (int i = 1; i <= m; i++) {
while (top >= 2) {
Point t = met(stk[top - 1], stk[top]);
if (!check(l[i].a, l[i].b, t)) top--; // 如果不在左边就弹出
else break;
}
stk[++top] = l[i];
}
while (top >= 3) {
Point t = met(stk[top - 1], stk[top]);
if (!check(stk[1].a, stk[1].b, t)) top--;
else break;
}
int now = 1;
while (top - now + 1 >= 3) {
Point t = met(stk[now], stk[now + 1]);
if (!check(stk[top].a, stk[top].b, t)) now++;
else break;
}
for (int i = now; i < top; i++) ans[++cnt] = met(stk[i], stk[i + 1]);
ans[++cnt] = met(stk[now], stk[top]);
// for (int i = now; i <= top; i++) cout << stk[i].a.x << ' ' << stk[i].a.y << '\t' << stk[i].b.x << ' ' << stk[i].b.y << endl;
// for (int i = 1; i <= cnt; i++) cout << ans[i].x << ' ' << ans[i].y << endl;
double S = 0;
for (int i = 1; i <= cnt; i++) S += cha(ans[i], ans[i % cnt + 1]);
printf("%.3lf\n", fabs(S) / 2);
return 0;
}
五、闵可夫斯基和
两个图形 \(A,B\) 的闵可夫斯基和定义为:
这里只介绍凸包的闵可夫斯基和。
怎么求?实际上就是把 \(B\) 图形绕着 \(A\) 的边转一圈,中途 \(B\) 覆盖过的点集就是闵可夫斯基和。
这很魔怔,瞪眼法可得:把 \(A,B\) 的边按极角排序,再拼在一起,就得到了闵可夫斯基和的结果。
但是拼接后可能会存在三点共线情况,但这并不会影响什么,可以直接特判,也可以再求一遍凸包解决。
例 10:洛谷 P4557 [JSOI2018] 战争
首先,一个部落的“领地”可以被刻画成点集构成的凸包。
不妨设两个凸包分别为 \(A,B\),将凸包内的点集刻画为向量的形式,即一个点 \((x, y)\) 看作 \((0, 0) \to (x, y)\) 的向量:
设两个点(向量)\(a, b\) 分别来自 \(A, B\),则对于一次询问需要查询:是否存在 \(a, b\) 满足 \(a = b + (dx, dy)\)。
即:
存在 \(a \in A, b \in B\),使得 \(a-b = (dx, dy)\)。
但存在这一条件并不好支持查询,换一个角度,求出 \(C = {a-b | a \in A, b \in B}\) 这个全集判定 \((dx, dy)\) 是否在这之内?
\(A,B\) 都是凸包,求 \(A-B\)。凸包减法?什么玄学东西?
显然可以把 \(B\) 中坐标全部取反,然后变成 \(A + (-B)\)。
\(-B\) 显然也是凸包,那么就变成了凸包加法,联想到闵可夫斯基和。
因此我们的思路是:先求出 \(A,-B\),再求出 \(A-B\) 的闵可夫斯基和凸包 \(C\),对于每次询问判定 \((dx, dy)\) 是否在 \(C\) 之内。
这是之前提过的问题,不再赘述。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int q;
struct Point { int x, y; } ;
inline long long cha(Point a, Point b) { return a.x * 1ll * b.y - b.x * 1ll * a.y; }
inline int check(Point a, Point b, Point c) { // c 是否在有向直线 a->b 的逆时针方向(左侧,含)
b.x -= a.x, b.y -= a.y, c.x -= a.x, c.y -= a.y;
long long res = cha(b, c);
if (res == 0) return 0;
if (res > 0) return 1;
return -1;
}
inline bool online (Point a, Point b, Point c) { // c 在线段 ab 上
int x = min(a.x, b.x), xx = max(a.x, b.x);
int y = min(a.y, b.y), yy = max(a.y, b.y);
return (check(a, b, c) == 0 && x <= c.x && c.x <= xx && y <= c.y && c.y <= yy) ;
}
inline bool cmp(Point a, Point b) { return (a.x == b.x) ? a.y < b.y : a.x < b.x; } // 二维排序
struct Polygon {
int n, top;
Point a[N], stk[N];
inline void input(bool opt) {
for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y);
if (opt) for (int i = 1; i <= n; i++) a[i].x = -a[i].x, a[i].y = -a[i].y;
}
inline void convex() {
sort(a + 1, a + 1 + n, cmp);
stk[++top] = a[1], stk[++top] = a[2];
for (int i = 3; i <= n; i++) {
while (top >= 2 && check(stk[top - 1], stk[top], a[i]) <= 0) top--;
stk[++top] = a[i];
}
int tt = top;
stk[++top] = a[n - 1];
for (int i = n - 2; i >= 1; i--) {
while (top > tt && check(stk[top - 1], stk[top], a[i]) <= 0) top--;
stk[++top] = a[i];
}
for (int i = 1; i <= top; i++) a[i] = stk[i];
n = --top;
}
// 以下是 C 凸包函数
inline void add(Point t) { a[++n] = t; }
inline void uniq() { // 去掉三点共线
top = n, n = 1;
for (int i = 1; i <= top; i++) stk[i] = a[i];
for (int i = 2; i <= top; i++) a[i].x = a[i].y = 0;
for (int i = 2; i <= top; i++)
if ((stk[i].x * 1ll * a[n].y) ^ (stk[i].y * 1ll * a[n].x)) a[++n] = stk[i];
else a[n].x += stk[i].x, a[n].y += stk[i].y;
}
} A, B, C;
inline void trans() { // 求出闵可夫斯基和凸包 C
int t1 = 1, t2 = 1;
while (t1 <= A.n && t2 <= B.n) {
Point deltaA = (Point){A.a[t1 + 1].x - A.a[t1].x, A.a[t1 + 1].y - A.a[t1].y};
Point deltaB = (Point){B.a[t2 + 1].x - B.a[t2].x, B.a[t2 + 1].y - B.a[t2].y};
if (t1 <= A.n && check((Point){0, 0}, deltaA, deltaB) >= 0) C.add( deltaA ), t1++;
else C.add( deltaB ), t2++;
}
while (t1 <= A.n) C.add( (Point){A.a[t1 + 1].x - A.a[t1].x, A.a[t1 + 1].y - A.a[t1].y} ), t1++;
while (t2 <= B.n) C.add( (Point){B.a[t2 + 1].x - B.a[t2].x, B.a[t2 + 1].y - B.a[t2].y} ), t2++;
C.uniq();
C.a[0] = (Point){A.a[1].x + B.a[1].x, A.a[1].y + B.a[1].y};
for (int i = 1; i <= C.n; i++) C.a[i].x += C.a[i - 1].x, C.a[i].y += C.a[i - 1].y;
// for (int i = 0; i <= C.n; i++) cout << C.a[i].x << ' ' << C.a[i].y << endl;
C.n--;
}
int main() {
scanf("%d%d%d", &A.n, &B.n, &q);
A.input(0), B.input(1);
A.convex(), B.convex();
// for (int i = 1; i <= B.n; i++) cout << B.a[i].x << ' ' << B.a[i].y << endl;
trans();
while (q--) {
int dx, dy; scanf("%d%d", &dx, &dy);
Point p = (Point){dx, dy};
if (check(C.a[0], C.a[1], p) < 0) { putchar('0'); putchar('\n'); continue; }
if (check(C.a[C.n], C.a[0], p) < 0) { putchar('0'); putchar('\n'); continue; }
int l = 1, r = C.n;
while (l < r) {
int mid = l + r + 1 >> 1;
if (check(C.a[0], C.a[mid], p) >= 0) l = mid;
else r = mid - 1;
}
// [l, l + 1] 两条边之间
if (check(C.a[l], C.a[l + 1], p) > 0 || online(C.a[l], C.a[l + 1], p) ) putchar('1');
else putchar('0');
putchar('\n');
}
return 0;
}
六、最小圆覆盖
给定平面上 \(n\) 个点,求覆盖这些点的最小圆的圆心和半径。
不妨用增量法,逐渐加入点并计算新的最小圆。
当 \(n=1\) 的时候,最小圆覆盖当然圆心是第一个点 \(p_1\),半径为 \(0\)。
当 \(n=2\) 的时候,最小圆覆盖就是两点定圆。
当 \(n=3\) 的时候,分为两种情况:
- \(p_3\) 在上一个圆的圆周上或圆内。这种情况不会影响最小圆覆盖,忽略这个点。
- \(p_3\) 在上一个最小圆覆盖圆之外。这个时候 \(p_3\) 一定在前三个点的最小圆覆盖的圆周上,才能满足“最小”的性质。那么现在原问题转化为子问题:从 \(p_1p_2\) 中找出一或两个点,与点 \(p_3\) 两点定圆或三点定圆。
- 当 \(n \geq 4\) 的时候,与 \(n=3\) 的时候同理,分为两种情况,第一种直接忽略这个点,第二种则是从前面的点中挑出一或两个与 \(p_4\) 一起定圆。
最后把所有的点都加入之后,就可以得出最小圆覆盖。
需要一层循环枚举所有的点进行加入,一层循环来枚举两点定圆,还需要一层循环来枚举三点定圆(假设现在会两点定圆和三点定圆)。
所以这个算法的时间复杂度是 \(O(n^3)\)。
事实上,把增量法改进为随机增量法就可以优化到 \(O(n)\),具体地,在执行算法之前把点打乱顺序。
时间复杂度证明:
由于三点定圆,所以对于 \(n\) 个点中,每个点参与三点定圆计算的概率不超过 \(\frac{3}{n}\)。
由于只有更新半径才会往下一层循环,找另一个点(详见代码)所以对于当前层的第 \(i\) 个点,它往下找的概率不超过 \(\frac{3}{i}\)。
- 对于第三层,每个点参与计算的概率为 \(1\),由于只有参与和不参与两种状态,所以期望等于概率为 \(1\),总复杂度为 \(\sum\limits_{i=1}^{n} 1 = O(n)\)。
- 对于第二层,有 \(O(n) + \sum\limits_{i=1}^{n} \frac{3}{i} \times O(n) = O(n)\)。
- 对于最外层,有 \(O(n) + \sum\limits_{i=1}^{n} \frac{3}{i} \times O(n) = O(n)\)。
得证期望总复杂度为 \(O(n)\)。
关于如何两点定圆和三点定圆?
两点定(最小)圆是简单的,圆心是 \(p_1, p_2\) 的中点,半径是线段长度的一半。
三点定圆较为复杂,但列个方程就解完了。
设三个点分别为 \((x_1, y_1), (x_2, y_2), (x_3, y_3)\)。
圆心为 \((x,y)\) 半径为 \(r\)。
展开:
\((2)\) 式减 \((1)\) 式,得:
整理式子移项,同理 \((3)\) 式减 \((1)\) 式整理可得:
将系数换元化简:
解得
圆的半径求一下距离即可。
例 11:洛谷 P1742 最小圆覆盖
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const int N = 5e5 + 5;
struct Point { double x, y; };
inline double dis(Point A, Point B) { A.x -= B.x, A.y -= B.y; return sqrt(A.x * A.x + A.y * A.y); }
Point circle_center(const Point A, const Point B, const Point C) {
// ax + by = c
// dx + ey = f
double a = 2 * (A.x - B.x), b = 2 * (A.y - B.y), c = A.x * A.x + A.y * A.y - B.x * B.x - B.y * B.y;
double d = 2 * (A.x - C.x), e = 2 * (A.y - C.y), f = A.x * A.x + A.y * A.y - C.x * C.x - C.y * C.y;
double y = (a * f / d - c) / (a * e / d - b);
double x = (c - b * y) / a;
return (Point){x, y};
}
void min_cover_circle(Point * p, int n, Point &c, double &r) {
random_shuffle(p + 1, p + 1 + n);
c = p[1]; r = 0;
for (int i = 2; i <= n; i++) {
if ( dis(p[i], c) - r > eps ) {
c = p[i]; r = 0;
for (int j = 1; j < i; j++)
if ( dis(p[j], c) - r > eps ) {
c.x = (p[i].x + p[j].x) / 2;
c.y = (p[i].y + p[j].y) / 2;
r = dis(p[j], c);
for (int k = 1; k < j; k++)
if ( dis(p[k], c) - r > eps ) {
c = circle_center(p[i], p[j], p[k]);
r = dis(p[i], c);
}
}
}
}
}
int n;
Point p[N], c;
double r;
int main() {
while (~scanf("%d", &n) && n) {
for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
min_cover_circle(p, n, c, r);
printf("%.10lf\n%.10lf %.10lf", r, c.x, c.y);
}
return 0;
}
*例 12:洛谷 P4586 [FJOI2015] 最小覆盖双圆问题
给定平面上 \(n\) 个点 \((x_1,y_1),\dots,(x_n,y_n)\),找出 \(2\) 个半径相同的圆 \(R_1\) 和 \(R_2\),覆盖给定的 \(n\) 个点,且半径最小。
设计一个算法,计算出所求最小覆盖双圆 \(R_1\) 和 \(R_2\) 的半径。
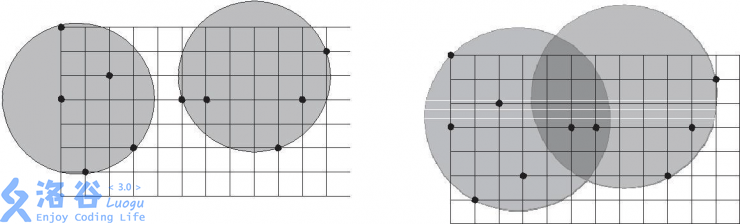
很显然的,既然要分成两个圆,那么一定是用一条直线分割成两个点集,然后分别求出两个点集的最小圆覆盖的半径 \(r_1r_2\),答案就是 \(\max(r1,r2)\)。
要求出这条直线的位置,其实很容易地可以想到用二分。
这里所说的是:用二分求出一条与 \(X\) 轴垂直的直线,然后再求解。
但是还有一种情况未考虑——如果正解是斜着画一条直线呢?
斜着划直线并不好做,不妨直接把整个坐标轴旋转。
每次旋转之后都求一次最小双圆覆盖,然后再取最优值即是答案。问题就在于如何对每个点进行“旋转”?
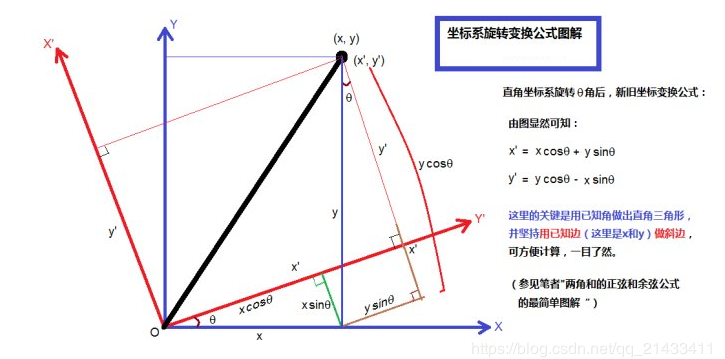
对于这个坐标系,只需要旋转 \(180\) 度就可以了,因为把坐标系旋转 \(180\) 度后就又回到了第一次计算的问题。
有一个很重要的优化:在二分的时候,如果当前的 \(\min(r1,r2)\) 无法更新答案,则后面都无法更新答案,直接退出二分。
复杂度 \(O(C n \log n)\),其中 \(C\) 为常数,\(C=180\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号