浅谈高斯消元

Upd on 2025.4.22: 初一的我文笔好幼稚啊，改一下文章风格。

我们先来看一下高斯消元的过程：

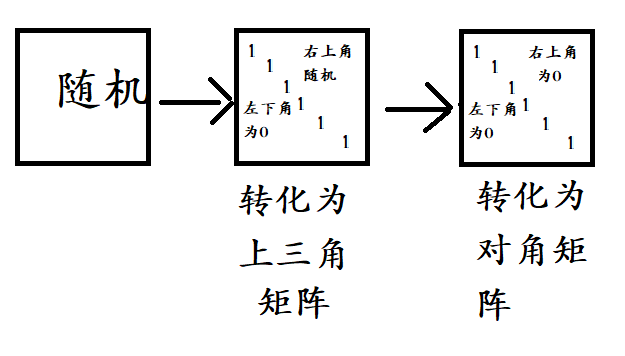
图中那三个方框就是高斯消元中的“系数矩阵”，我们先看第三个方框。
可以看到第三个“对角矩阵”对角的这一条线，系数都是1。
所以等式的另一边就是方程的解。
可是如何将随机系数矩阵转化为上三角矩阵，又如何将上三角矩阵转化为对角矩阵呢？
了解了高斯消元的过程，我们就可以开始详细地说明具体过程了。

---

我们可以先从枚举列的角度考虑：

1. 找主元

   • 主元就是这一列里绝对值最大的一个。
   • 注意一定是最大！

2. 交换

   • 将主元所在的一行交换到系数矩阵的最上方。

3. 归一

   • 把这一行的第一个数化为1。
   • 但是如何操作呢？
   • 也就是等式两边同时除以第一个系数。

4. 消元

   • 将后面所有行的这一列消成0。

因为高斯消元里面有除法，所以要用 $double$ 存储！
时间复杂度 $O(n^3)$

例题：球形空间产生器