浅谈后缀数组相关
零、前言
字符串滚出 OI!这破字符串一题都做不下去了。
一、后缀数组
定义
考虑这样一个问题如何求解:
定义 \(Suf_i\) 表示 \(S_{[i,n]}\),即 \(i\) 开始的一段后缀,其编号为 \(i\)。
对字符串 \(S\) 的每个下标 \(i\),求出 \(Suf_i\) 在所有后缀中按字典序排序的排名。
- 记 \(sa_i\) 为所有后缀排序之后,第 \(i\) 小的后缀编号。
- 记 \(rk_i\) 表示编号为 \(i\) 的后缀排名是多少。
根据定义显然有 \(sa_{rk_i} = rk_{sa_i} = i\),那么只要知道 \(sa,rk\) 其一就可以线性地算出另一个。
求解
算法 1:暴力排序 \(O(n^2 \log n)\)
字符串比较复杂度 \(O(n)\),排序复杂度 \(O(n \log n)\),总复杂度 \(O(n^2 \log n)\)。
这不多说了。
算法 2:倍增 \(O(n \log^2 n)\)
考虑从小到大枚举 \(2^k\),计算从 \(i\) 开始往后长度为 \(2^k\) 的字符串的 \(rk^k\)。
事实上,第 \(k\) 轮的 \(rk^k\) 可以由 \(k-1\) 轮的 \(rk^{k-1}\) 算出。
这个倍增的过程相当于把 \([i,i+2^{k-1}-1]\) 和 \([i+2^{k-1},i+2^k-1]\) 两个子串合并,也就相当于把 \(rk^{k-1}_i\) 和 \(rk^{k-1}_{i+2^{k-1}-1}\) 合并。
子串合并是首尾相接,那排名合并相当于合并为一个二元组,进行双关键字排序。
这样每次合并之后暴力 sort 复杂度为 \(O(n \log n)\),外面套一层倍增,因此总复杂度 \(O(n \log^2 n)\)。
算法 3:倍增 + 计数排序 + 基数排序 \(O(n \log n)\)
倍增不能再优化了,现在瓶颈在于内部的 sort 排序。
能否将其优化为 \(O(n)\)?可以!
发现参与排序的元素都是上一轮的排名,因此值域是 \(O(n)\),启发我们使用计数排序。
但是这是双关键字啊?也很简单,先对第二关键字排,再对第一关键字排,这里使用了基数排序的技巧。
算法 3 优化
优化 1
事实上不需要对第二关键字排序。
因为两个关键字都是上一轮排序的排名,即 \(rk^{k-1}\),是单调的。
对于 \(i+2^k \leq n\),它的第二关键字是有序的;对于 \(i+2^k \gt n\),钦定它的第二关键字是 \(-\infty\)。
因此这个“排序”相当于把所有 \(i+2^k \gt n\) 的下标移到最前面,其余的顺次往后移。
优化 2
实时计算计数排序的值域。
优化 3
如果值域已经是 \([1,n]\),那么说明每个后缀的排名都不同,因此再往后比较已经无意义。
算法 4:SA-IS \(O(n)\);算法 5:DC3 \(O(n)\)
事实上 \(O(n \log n)\) 的算法已经适用于绝大多数场景,因此 \(O(n)\) 算法不再赘述。
代码 \(O(n \log n)\)
int sa[N], rk[N], pre[N], cnt[N];
int x[N], y[N]; //令 x 表示第一关键字排序的结果,y 表示第二关键字排序的结果
void init_SA() {
int v = 128;
for (int i = 0; i <= v; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) ++cnt[ x[i] = (int)s[i] ]; //初始以 ASCII 作为排序依据
for (int i = 1; i <= v; i++) cnt[i] += cnt[i - 1]; //计数排序,前缀和桶
for (int i = n; i >= 1; i--) sa[ cnt[x[i]]-- ] = i; //计数排序计算初始 sa 数组
for (int len = 1; ; len <<= 1) {
int tot = 0;
for (int i = n - len + 1; i <= n; i++) y[++tot] = i; //这些第二关键字默认为 -INF,直接平移到最前面
for (int i = 1; i <= n; i++) //注意 sa[i] 的含义是第 i 小的后缀编号,因此从小到大遍历是有序的,将它们按照第二关键字顺序插入即可
if (sa[i] > len) y[++tot] = sa[i] - len;
// y[i] 表示以第二关键字排序,第 i 小的后缀下标,则 x[y[i]] 表示再按照第一关键字排序的排名
// 因此这里计数排序和开头有区别
for (int i = 0; i <= v; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) ++cnt[ x[i] ];
for (int i = 1; i <= v; i++) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--) sa[ cnt[x[y[i]]]-- ] = y[i], y[i] = 0;
// 接下来需要更新新的 x 数组,且需要使用之前的 x 数组。
// 因此可以直接把 x 和 y 交换,接下来 y 代表 old_x
tot = 0;
for (int i = 0; i <= n + 5; i++) y[i] = x[i], x[i] = 0;
for (int i = 1; i <= n; i++) {
if (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + len] == y[sa[i - 1] + len]) x[sa[i]] = tot;
else x[sa[i]] = ++tot;
}
v = tot;
if (v == n) break; //排好序了
}
}
二、\(\text{Height}\) 数组
定义
首先定义 \(\text{LCP}(S,T)\) 表示 \(S,T\) 两个字符串的最长公共前缀。
然后定义 \(\text{Height}\) 数组:\(height_i = \text{LCP}(suf_{sa_i}, suf_{sa_{i-1}})\)。
特殊地,\(height_1 = 0\)。
性质
证明略。
应用 1:求两子串的 \(\text{LCP}\)
将两个子串的 LCP 转化为 RMQ 问题。
应用 2:比较两子串大小
假设两个子串分别为 \(S[a,b]\) 和 \(S[c,d]\),需要比较大小。
若 \(\text{LCP}(suf_a,suf_c) \geq \min(b-a+1,d-c+1)\),则 \(S[a,b] \lt S[c,d]\) 等价于 \(b-a+1 \lt d-c+1\),因为一定满足一个是另一个的子串。
否则 \(S[a,b] \lt S[c,d]\) 等价于 \(rk_a \lt rk_c\)。
应用 3:求所有子串去重后的数量
子串等价于后缀的前缀,考虑容斥,用总数减去重复数量。
则答案为 \(\frac{n(n+1)}{2} - \sum\limits_{i=2}^{n} height_i\),因为 \(height\) 的定义是 \(\text{LCP}\) 长度。
应用 4:求出现了至少 \(k\) 次的子串最大长度是多少
和上一个应用思路类似。由于子串等价于后缀的前缀,相当于在后缀排序之后一段连续后缀的公共前缀。
由公共前缀联想到 \(\text{LCP}\),又因为至少出现 \(k\) 次,因此只要在排序之后求所有长度为 \(k-1\) 的区间的 \(height\) 最大值即可。
求解
有了上面这条性质,就可以暴力求解了,复杂度是 \(O(n)\)。
代码
int ht[N];
void init_height() {
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, j = 0, now = 0; i <= n; i++) {
if (rk[i] == 1) { ht[rk[i]] = 0; continue; } // 默认 h[1] = 0;
j = sa[rk[i] - 1]; now = max(now - 1, 0);
while (i + now <= n && j + now <= n && s[i + now] == s[j + now]) now++; //暴力扩展
ht[rk[i]] = now;
}
}
三、例题
标红 \(\color{red}{\texttt{Code}}\) 之前的内容是提示,后面是题解。
1. 洛谷 P3809 【模板】后缀排序
模板,求 sa 数组和 height 数组。
2. 洛谷 P2852 USACO06DEC Milk Patterns G
说实话这么小的数据范围一眼二分再开个 map 搞一下 hash 就能过去了。
但这毕竟是后缀数组练习题。
对应 height 数组应用 4,\(\color{red}{\texttt{Code}}\)。
由于子串等价于后缀的前缀,相当于在后缀排序之后一段连续后缀的公共前缀。
由公共前缀联想到 \(\text{LCP}\),又因为至少出现 \(k\) 次,因此只要在排序之后求所有长度为 \(k-1\) 的区间的 \(height\) 最大值即可。
3. P4248 [AHOI2013] 差异
只要学会了 SA 就是简单题。\(\color{red}{\texttt{Code}}\)。
这题是紫的?估计难度全在模板了吧。
后面相当于 height 数组的区间最小值之和。
4. 洛谷 P3181 [HAOI2016] 找相同字符
简单容斥转化为单字符串问题,然后和上一题一样的做法。\(\color{red}{Code}\)。
求两个字符串各取子串相同的方案数,这很麻烦,我们现在只知道一个子串中的方案数。
但是可以把两个字符串合并,为了防止算重中间加一个特殊符号例如 #,再用容斥减去两个字符串内部的情况即可。
5. 洛谷 P2408 不同子串个数
height 数组应用 3。\(\color{red}{\texttt{Code}}\)。
子串等价于后缀的前缀,考虑容斥,用总数减去重复数量。
则答案为 \(\frac{n(n+1)}{2} - \sum\limits_{i=2}^{n} height_i\),因为 \(height\) 的定义是 \(\text{LCP}\) 长度。
6. P4070 [SDOI2016] 生成魔咒
height 数组结合 ST 表。\(\color{red}{\texttt{Code}}\)。
从前往后加入字符,对每个前缀求有多少本质不同子串。
并不难想到后缀数组,但是对每个前缀都求一次肯定是爆表的,因为每次在后面加一个字符改动的 \(ht\) 数组是 \(O(n)\) 级别。
然而一个很巧妙的做法是把字符串倒序,这样每次在最前面加入一个字符。
这样不会改变答案,而且在最前面加入一个字符相当于插入一个 \(ht\)!
注意其实本质不同子串数可以表示为 \(\sum\limits_{i=1}^{n} n - sa_i + 1 - ht_i\),可以通过此公式算出任意一个前缀的答案。
7. 洛谷 P5341 [TJOI2019] 甲苯先生和大中锋的字符串
height 数组结合单调队列、差分。\(\color{red}{\texttt{Code}}\)。
首先只要学过 SA 就并不难刻画“恰好出现 \(k\) 次”这一条件。
设 \(u\) 为 \([l,r]\) height 的 \(\min\),且 \(r-l+1\) 即区间长度为定值 \(k-1\),这个可以用单调队列简单维护。
则 \([1,u]\) 的前缀出现次数显然不小于 \(k\),至于恰好为 \(k\) 只需要钦定 \(d = \max(ht_{l-1},ht_{r+1})\) 就行了,合法的长度区间为 \([d+1,u]\),相当于这个区间出现次数 \(+1\)。
现在需要一个数据结构支持区间 \(+1\) 和全局查询最大值。由于查询在加法之后因此可以用差分。
对于 \(k=1\),由于单调队列区间长度为 \(k-1=0\),需要特殊处理它的 \(u\) 为 \(n-sa_i+1\) 即后缀长度。
8. 洛谷 P2178 [NOI2015] 品酒大会
height 数组模型转化后结合并查集。\(\color{red}{\texttt{Code}}\)。
首先 \(ans_i\) 的答案可以从 \(ans_{i+1}\) 累加过来,因此我们考虑相似度恰好为 \(i\) 对答案的贡献。
相当于两个后缀 \(a,b\) 的 LCP 长度恰好为 \(i\),即 \([rk_a,rk_b]\) 的 \(\min \{ height \}\) 必须恰好等于 \(i\)。
这玩意儿很难做,但是我们可以考虑从大到小加入 Height。
这样转化的巧妙之处在于 \(\lt i\) 的 height 都没有被加入,因此不会影响统计。
那么加入一个 height 相当于是合并两个连通块,同时还要维护连通块的 \(\max,\min,siz\)。
9. 洛谷 P3975 [TJOI2015] 弦论
height 数组结合神秘二分。 \(\color{red}{\texttt{Code}}\)。
貌似可以逐位确定?
题解区又是一堆看不懂的 SAM,这里试图提供 SA 做法,但写的很乱。
\(t=0\) 是好做的。
根据笔记第六题【生成魔咒】可知:
注意其实本质不同子串数可以表示为 \(\sum\limits_{i=1}^{n} n - sa_i + 1 - ht_i\),可以通过此公式算出任意一个前缀的答案。
因此相当于是算第 \(k\) 小的本质不同子串,直接从小到大遍历后缀直到发现目标串在当前后缀内。
\(t=1\) 咋做啊?是不是有二分什么的做法降低复杂度?
直接求排名为 \(k\) 的子串很难,考虑换一个角度,二分之后求一个子串的排名(可重)。
由于 \(t=1\) 的子串一定在 \(t=0\) 中出现过,所以考虑将所有子串排序后二分答案,即二分答案是去重之后的第 \(ans\) 个子串。
子串排序也不好做,那就把后缀排序,利用 height 数组求排名。
现在求排序后第 \(x\) 个后缀长度为 \(len\) 的前缀这一子串的排名:
由于后缀数组的性质,\([1,x-1]\) 后缀显然字典序小于 \(x\);又因为可重,需要把 \([x,n]\) 的 LCP 也算进去。
二分返回值要开 long long。
10. 洛谷 P9482 [NOI2023] 字符串
要是场上遇到这种题就算会做心态也先崩了,但其实码力要求并不高。
height 数组结合 ST 表、可持久化线段树、二分。\(\color{red}{\texttt{Code}}\)。
看到题目很自然地想到 SA 处理子串问题。
然后怎么搞 \([a,b]\) 的所有子串和 \([c,d]\) 子串的 LCP?
完全不会做啊,先骗 \(40\) 分吧。
直接枚举 \([a,b]\) 中选择子串的左端点 \(t\),然后相当于是 \([t,n]\) 后缀与 \([c,n]\) 后缀进行匹配,求 LCP。
然后再和 \(\min(b-t+1,d-c+1)\) 取 \(\min\) 即可。
时间复杂度 \(O(nm)\)。
首先不难注意到答案是有单调性的,如果 \(ans\) 满足条件,那么 \(ans-1\) 一定也满足条件。
有单调性一定可以二分,现在考虑如何判定 \(ans\) 是否满足条件?
相当于判定 \([a,b-ans+1]\) 是否有一个 \(t\),且 \(\text{LCP}(t,c) \geq ans\)。
注意到如果固定 \(c\),LCP 关于 rk 也是有单调性的。
可以转化为二分出 \([l,r]\) 满足 \(\forall x \in [l,r]\) 都有 \(\text{LCP}(x,c) \geq ans\),且 \([l,r]\) 是极长的。
然后相当于求 \([a,b-ans+1]\) 内有没有 \([l,r]\) 的点。
二维数点!可持久化线段树秒了!
11. 洛谷 P1117 [NOI2016] 优秀的拆分
需要找到合适的 \(O(n^2)\) 算法优化。部分 \(O(n^2)\) 算法还优化不了 T_T。
可以 hash 干过去,但是 \(O(n \log^2 n)\)。\(\color{red}{\texttt{Code}}\)。
全是套路,全都不会,但关键点这一转化确实比较难想。
下文记 \(pre_i\) 表示 \([1,i]\) 这一段字符串前缀,\(suf_i\) 表示 \([i,n]\) 这一段字符串后缀,\(S[i,j]\) 表示 \([i,j]\) 这段子串。
最开始想过设什么 \(f_{i,j}\) 表示 \([i,j]\) 是否是 \(\texttt{AA}\) 型字符串,\(g_{i,j}\) 表示 \([i,j]\) 的优秀拆分方案数,但这样 \(O(n^2)\) 的做法很难优化,状态就已经二维了。
所以设 \(l_i\) 表示以 \(i\) 为左端点的 \(\texttt{AA}\) 型字符串数量,\(r_i\) 表示以 \(i\) 为右端点的 \(\texttt{AA}\) 型字符串数量。
答案即为 \(\sum\limits_{i=1}^{n-1} r_i \times l_{i+1}\)。
有很多方法预处理 \(l,r\),但是有些并不好优化,因此考虑下面这种预处理方法:
既然正向的都不好做,那就反向枚举 \(\texttt{AA}\) 中 \(\texttt{A}\) 的长度 \(len\)。
枚举点对 \((i,j)\),其中 \(i+len=j\)。
若满足 \(\text{LCP}(suf_i,suf_j) \geq len\),那么显然有 \(S[i,j-1]=S[j,j+len-1]\),因此 \(r_{j+len-1} \leftarrow r_{j+len-1} + 1\),\(l\) 数组的计算同理。
其中 LCP 可以用后缀数组 \(O(1)\) 求解,枚举 \(len,i\) 复杂度为 \(O(n^2)\)。
如何优化?
考虑设“关键点”。
还是枚举 \(len\),每间隔 \(len-1\) 个标记一个“关键点”,那么 \(\texttt{A}\) 子串一定至少经过一个关键点。
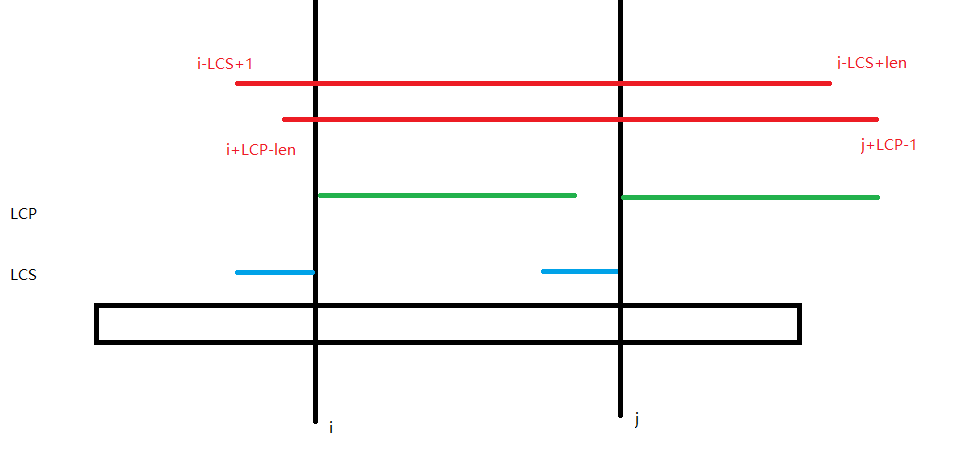
考虑求出 \(\text{LCS}(pre_i,pre_j)\) 和 \(\text{LCP}(suf_i,suf_j)\),如果两者的和 \(\geq len\) 那么显然可以组成 \(\texttt{AA}\) 型字符串。
然后发现 \(l,r\) 每次都是一段区间加上 \(1\),可以用差分维护。
至于前后缀的 \(\text{LCS}\) 和 \(\text{LCP}\),可以对原串和反串跑 SA。
这样枚举 \(len\) 是调和级数,预处理 SA 是 \(O(n \log n)\),因此总复杂度为 \(O(n \log n)\),数据范围还是开太小了。
由于 LCP 和 LCS 可能很长,会导致重复计算,因此要和 \(len\) 取 \(\min\)。
12. 洛谷 P3763 [TJOI2017] DNA
注意 \(3\) 次“失配”要怎么利用,不妨从简单暴力的算法开始考虑。
然后再用后缀数组优化时间复杂度(其实不优化也能过)。\(\color{red}{\texttt{Code}}\)。
Hash、SA、FFT 都可以做。
\(3\) 次失配提示暴力匹配一段极长的。
具体地,枚举 \(S\) 串的每一个位置 \(i\),二分 hash 找到它和 \(T\) 串能匹配最长的长度,并往后跳,最多跳 \(3\) 次。
这样复杂度为 \(O(n \log n)\),且 hash 容易被卡。
我们有更好的做法,用后缀数组。
先把两个串拼在一起求 \(\text{sa}\) 和 \(\text{height}\),然后利用 ST 表 \(O(1)\) 查询最长匹配长度。
这样复杂度 \(O(n)\) 且正确性有保证。
FFT 算法只是将 hash 部分改成 FFT 匹配罢了,多此一举。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号