计算几何相关

感觉没啥动力去学新知识了。

扫描线

扫描线直接照搬了...这篇主要是给之后的积分和凸包之类留的。

就是用线段树解决计算几何问题。

如何处理平面内一群矩形的面积交？

考虑用面积的朴素定义，\(S=ab\)，相当于一堆面积合到一起就是 \(b\) 个可以不同的 \(a\) 相加。

我们维护坐标系的 \(x\) 值，再去跳 \(y\) 轴。具体地，只有一个矩形的下边界和上边界才会对当前 \(x\)，也就是 \(a\) 值之和造成影响。我们记录一下矩形的上下底面，在下底面 \(y\) 值加上它覆盖的 \(x\) 段，在它的上底面减去它的 \(x\) 段，按照 \(y\) 给这些操作排序后去跳 \(y\)，该加加改减减。线段树维护当前 \(y\) 内的 \(x\) 之和，相当于会形成很多的长度段，一堆叠在一起也算一个，瞎搞一下维护即可，\(S=\sum \Delta y*x_i\)。

放个代码方便复习。

#include<bits/stdc++.h>
#define MAXN 1000005
#define int long long
using namespace std;
int n;
struct node{
	int x1,x2,y;
	int opt;
}sq[MAXN<<1];
inline bool cmp(node a,node b){
	if(a.y==b.y)return a.opt>b.opt;
	return a.y<b.y;
}
int mp[MAXN<<2];
int ans,tmp;
struct Segment_Tree{
	#define ls(p) p<<1
	#define rs(p) p<<1|1
	struct TREE{
		int l,r;
		int val,tag;//维护一个当前x段的覆盖层数和贡献，只要有层数就有贡献，没层数就没贡献
	}tree[MAXN<<3];
	inline void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].tag=0;
		if(l==r)return;
		int mid=l+r>>1;
		build(l,mid,ls(p));
		build(mid+1,r,rs(p));
	}
	inline void push_up(int p){//主要看看pushup即可
		if(tree[p].tag)tree[p].val=mp[tree[p].r+1]-mp[tree[p].l];
		else{
			tree[p].val=tree[ls(p)].val+tree[rs(p)].val;
		}
	}
	inline void modify(int l,int r,int k,int p){
		if(mp[tree[p].r+1]<=l||mp[tree[p].l]>=r)return;
		if(mp[tree[p].l]>=l&&mp[tree[p].r+1]<=r){
			tree[p].tag+=k;
			push_up(p);
			return;
		}
	//	printf("nowmid=%lld,id=%lld,tree.l=%lld,tree.r=%lld\n",mid,p,tree[p].l,tree[p].r);
		modify(l,r,k,ls(p));
		modify(l,r,k,rs(p));
		push_up(p);
	}
}ST;
signed main(){
	scanf("%lld",&n);
	for(int i=1,x1,x2,y1,y2;i<=n;i++){
		scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
		sq[i]=(node){x1,x2,y1,1};
		sq[i+n]=(node){x1,x2,y2,-1};
		mp[i]=x1,mp[i+n]=x2;
	}
	sort(mp+1,mp+1+n*2);
	tmp=unique(mp+1,mp+1+2*n)-mp-1;
	//printf("tmp=%lld\n",tmp);
	sort(sq+1,sq+1+n*2,cmp);
	ST.build(1,tmp-1,1);
	//printf("ced\n");
	for(int i=1;i<n*2;i++){
	//	printf("solving %lld %lld %lldf\n",sq[i].x1,sq[i].x2,sq[i].opt);
		ST.modify(sq[i].x1,sq[i].x2,sq[i].opt,1);
		ans+=ST.tree[1].val*(sq[i+1].y-sq[i].y);
	}
	printf("%lld",ans);
	return 0;
}

计算周长

现在让你计算那坨矩形的周长。

同样的分析方法，矩形的下底面和上底面都会对当前答案做出贡献，但是贡献是 \(\Delta x\)，相当于新增的或新减少 x 的才是当前 \(y\) 的 \(x\) 贡献，自己画个图想去。

然后考虑竖条对答案的贡献，当前线段树覆盖的一堆线段会形成许多个分开的块，具象下来就是当前 \(y\) 区段实际参与计算的矩形个数。

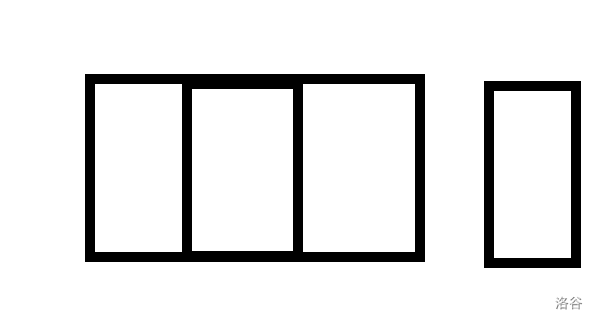
像是这张图虽然有三个矩形但只形成了两个块，因此实际的竖条个数是当前块数(2)乘以2。

用线段树再维护一下当前区段是否充满就可以推出来一共有几个块，满了就不加，不满就块数相加。

一道好玩的题

考虑用扫描线解决。

用矩形框点太蛋疼了，把点变成框那么大的矩形再用扫描线处理。

每个矩形相当于可以提供它权值的贡献，把这些贡献在 \(x\) 上叠加，发现线段树的极值就是当前 \(y\) 窗口能覆盖到的最大星星权值。没了。

自适应辛普森积分

挺简单的。

暴力展开一个二次函数的积分形式。

\[f(x)=ax^2+bx+c \]

\[\int_l^rf(x)dx=(r-l)(f(l)+4f(\frac{l+r}{2})+f(r))/6 \]

考虑这样一件事，对于一个要求积的函数 \(F(x)\)，递归直到和这个二次函数拟合后停止后汇总即可求得一个大概的积分，这就是辛普森法，然而缺点是像保证正确性就会特别慢，想跑快点就要牺牲正确性。

所以提出了自适应辛普森积分，因为对于整个函数肯定有长得比较像二次函数的和长得不太像二次函数的。对于长得像二次函数的可以少递归几次保证复杂度，长得不像的就多递归几次保证正确性。所以分治地进行这个过程，因为二次函数劈两半还是二次函数，对于当前要处理的区间 \([l,r]\) 与把它当作二次函数得到的积分值 \(ans\)，如果劈成两半 \([l,mid]\) 和 \([mid,r]\) 分开当二次函数求得的积分值之和 \(\sum\) 已经和 \(ans\) 十分接近了就说明这一段 \([l,r]\) 肯定是很像二次函数了，那就不递归了。反之，因为递归求解下去肯定不会丢失精度，重复上述过程直到拟合为止即可。

另外有一些正确性和复杂度上的优化。比如可以考虑钦定一个无论如何都要达到的递归层数 \(dep\) 来保证不丢精度，或者更改“十分接近”的定义即当前区间的 \(eps\) 来提速或者增加精度，还可以在递归之前扫一遍区间，直接跳过函数中可能存在的大片没有值的段来同时优化时间和正确性。

附上板子代码

#include<bits/stdc++.h>
#define db double
using namespace std;
db a,b,c,d,L,R;
const db eps=1e-7;
inline db f(db x){
	return (c*x+d)/(a*x+b);
}
inline db calc(db l,db r){
	db mid=(l+r)/2;
	return (r-l)*(f(l)+4*f(mid)+f(r))/6;
}
inline db asr(db l,db r,db eps,db ans){
//	printf("nowlr=%.5f %.5f\n",l,r);
	db mid=(l+r)/2.0;
	db lv=calc(l,mid),rv=calc(mid,r);
	if(fabs(lv+rv-ans)<=15*eps)return lv+rv+(lv+rv-ans)/15;
    else return asr(l,mid,eps/2,lv)+asr(mid,r,eps/2,rv);
}
signed main(){
	scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&L,&R);
	printf("%.6f\n",asr(L,R,eps,calc(L,R)));
	return 0;
}

三角形面积并

考虑一种类似扫描线的思路，设 \(F(x_0)\) 为坐标系内 \(x=x_0\) 这条竖线所截的图形段长度，这个可以 \(O(n)\) 扫一遍解出来一堆 \((y_s,y_e)\) 然后排序贪心 \(O(nlogn)\) 求和求出，然后答案即为

\[\int_{minX}^{maxX}F(x)dx \]

圆的面积并

一样的，随便写写就过了。

月下柠檬树

~~一样的，随便写写就过了。~~

但是毕竟是道黑是吧所以还是稍微记一下。

脑玩一下发现影子拍上去圆面积不变只有 \(x\) 坐标变了，投影则是若干个圆和相邻圆的两个外公切线（如果有的话）的并形式。

仍然积分法求，对于当前递归到而要求的 \(f(x_0)\)，先扫一遍包含那条线的圆能给的贡献（就是上一道题），然后看公切线怎么处理，草稿纸上划一下比如 \(\odot O_1\) 和 \(\odot O_2\) 圆心距为 \(x\) 则公切线所连半径和连心线夹角 \(\alpha\) 应有 \(cos\alpha=\frac{r_1-r_2}{x}\)，正弦直接拿1减然后就能表示出公切点的坐标了，判一下有没有穿过 \(x_0\) 然后就是三角形面积并的做法，弄完贡献直接取max就行了。

凸包

这些题真是计算几何吗我请问呢。

陶陶的难题

一眼分数规划，二分答案

\[A=\frac{y_i+q_j}{x_i+p_j}\Rightarrow A(x_i+p_j)=y_i+q_j \]

\[y_i-Ax_i+q_j-Ap_j\ge 0 \]

发现 \((x,y)\) 和 \((q,p)\) 本质是独立计算的，对于单个式子 \(y-Ax\) 取到极大值的点集显然是一个上凸壳的形式，直接用树剖维护重链上的凸壳，答案显然可以贪心取最大。

关于复杂度，凸壳二分自己带个 \(log\) 线段树和树剖俩 \(log\) 二分答案一个 \(log\) 复杂度 \(O(nlog^4n)\)。

旅行规划

实现一个 \(1e5\) 容量的数据结构：区间加等差数列，区间求最大前缀和。

考虑分块，维护单个块内的首项 \(s\) 和公差 \(d\)，然后整块内的单点可以表示为

\[a_i+b+id \]

\(a_i\) 较 \(a_j\) 优当且仅当

\[a_i-a_j>-d(i-j) \]

\[\frac{a_i-a_j}{i-j}>-d \]

是一个斜优的形式，考虑对整块维护凸包，散块暴力查。细节比较多。

妖怪

考虑钦定一只妖怪为最高战力时的 \((a,b)\) 区间，一只妖怪的战力为

\[atk+\frac{a}{b}dnf+dnf+\frac{b}{a}atk=\frac{a+b}{a}atk+\frac{a+b}{b}dnf \]

\(i\) 高于 \(j\) 当且仅当

\[\frac{a+b}{a}(atk_i-atk_j)>-\frac{a+b}{b}(dnf_i-dnf_j) \]

\[\frac{atk_i-atk_j}{dnf_i-dnf_j}>-\frac{a}{b} \]

进而维护上凸壳，\(i\) 左右侧的斜率 \(R,L\) 在 \(a,b\) 满足 \(L\le -\frac{a}{b}\le R\) 时会使 \(i\) 成为最强的怪兽，考虑在这段区间中使得它的战力最低，考虑一个基本不等式

\[atk+dnf+\frac{a}{b}dnf+\frac{b}{a}atk\ge atk+dnf+2\sqrt{atk*dnf} \]

当且仅当

\[a^2dnf=b^2atk,-a/b=K,K=-\sqrt{\frac{atk}{dnf}} \]

时等号成立，分讨一下在不在 \([L,R]\) 内，在就取，不在就取左右端点取最小。

向量集 & Linear Maximization

\[ax_i+by_i\ge ax_j+by_j \]

\[b(y_i-y_j)\ge -a(x_i-x_j) \]

\[\frac{y_i-y_j}{x_i-x_j}\ge -\frac{a}{b} \]

显然可以建线段树处理，但是这样复杂度是假的，因为每添加一下都要重构 \(O(log)\) 个凸包。

观察一下添加的形式：是按队列状添加的，而且询问肯定不会问还没添加的点，所以可以考虑先建出空的线段树，每次只有加入到当前区间的右端点时才push_up，这样复杂度就真了。

防线修建

动态维护凸包，时间倒流成加点然后用set实现一下就行了。

购票

相当于把鞋油dp转化到树上了

\[dp_u=min\{dp_v-dis_v*p_u+dis_u*p_u+q_u\} \]

这个是链上的转移，考虑挪到树上怎么处理，就需要考虑点分树上原父亲所在的那个点，直接放代码吧。

#include<bits/stdc++.h>
#define MAXN 200005
#define int long long
#define db double
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
const auto inf=1e18;
int n,_;
int fa[MAXN],s[MAXN],p[MAXN],q[MAXN],l[MAXN];
int dp[MAXN],dis[MAXN];
db K[MAXN];
struct node{
	int v,nxt;
}edge[MAXN<<1];
int h[MAXN],tmp;
inline void add(int u,int v){
	edge[++tmp]=(node){v,h[u]};
	h[u]=tmp;
}
bool vis[MAXN];
int sum,root,xv[MAXN],siz[MAXN];
inline void getrt(int u){
	xv[u]=0;
	siz[u]=1;
	for(int i=h[u];i;i=edge[i].nxt){
		int v=edge[i].v;
		if(vis[v])continue;
		getrt(v);
		siz[u]+=siz[v];
		xv[u]=max(xv[u],siz[v]);
	}
	xv[u]=max(xv[u],sum-siz[u]);
	if(root==-1||xv[u]<xv[root])root=u;
}
pii stac[2][MAXN];
int top[2];
inline void dfs(int u){
	if(l[u]>dis[u])stac[0][++top[0]]=mp(l[u]-dis[u],u);
	for(int i=h[u];i;i=edge[i].nxt){
		int v=edge[i].v;
		if(vis[v])continue;
		dis[v]=dis[u]+s[v];
		dfs(v);
	}
}
inline db slope(pii x,pii y){
	return (db)(y.se-x.se)/(db)(y.fi-x.fi);
}
inline void solve(int D,int val){
	while(top[1]>=2&&K[top[1]]>=slope(stac[1][top[1]],mp(D,val)))--top[1];
	stac[1][++top[1]]=mp(D,val);
	K[top[1]]=top[1]>=2?slope(stac[1][top[1]-1],stac[1][top[1]]):-inf;
}
inline int getans(int k){
	int l=1,r=top[1],res=0;
	while(r>=l){
		int mid=l+r>>1;
		if(K[mid]<=(db)k)res=stac[1][mid].se-k*stac[1][mid].fi,l=mid+1;
		else r=mid-1;
	}
	return res;
}
inline void work(int u){
//	printf("nowu=%lld\n",u);
	root=-1;
	getrt(u);
//	printf("root=%lld\n",root);
	vis[root]=1;
	int mem=root;
//	printf("mem=%lld\n",mem);
	if(mem!=u)sum-=siz[mem],work(u);
	top[0]=top[1]=dis[mem]=0;
//	printf("ined\n");
	dfs(mem);
//	printf("oed\n");
	sort(stac[0]+1,stac[0]+1+top[0]);
	int tar=mem,sav=0;
//	printf("top0=%lld\n",top[0]);
	for(int i=1;i<=top[0];i++){
	//	printf("nowi=%lld\n",i);
		int x=stac[0][i].fi,v=stac[0][i].se;
		while(tar!=fa[u]&&sav+s[tar]<=x&&fa[tar])sav+=s[tar],solve(sav,dp[fa[tar]]),tar=fa[tar];
		if(top[1])dp[v]=min(dp[v],dis[v]*p[v]+q[v]+getans(-p[v]));
	}
	for(int i=h[mem];i;i=edge[i].nxt){
		int v=edge[i].v;
	//	printf("vis %d=%d\n",v,vis[v]);
		if(vis[v])continue;
		sum=siz[v];
		work(v);
	}
}
signed main(){
	scanf("%lld%lld",&n,&_);
	for(int i=2;i<=n;i++){
		dp[i]=inf;
		scanf("%lld%lld%lld%lld%lld",&fa[i],&s[i],&p[i],&q[i],&l[i]);
		add(fa[i],i);
	}
	sum=n;vis[0]=1;
	work(1);
	for(int i=2;i<=n;i++)printf("%lld\n",dp[i]);
	return 0;
}

时空旅行

~~大抵是出题人发现加了yz太难所以给扔了~~

考虑一个线段树分治类似的思路，把一个星球存在的时间段放到线段树上维护，查询就是查询那个时间点的星球存在情况。

但是这样时空显然是炸的，怎么优化一下，式子转化为

\[Ans=(x_i-X)^2+c_i \]

\[2Xx_i+Ans=x_i^2+X^2+c_i \]

是一个斜优的形式，且是一个斜率递增的凸包，那就可以给询问的 \(X\) 和待插入的 \(x_i\) 分别排序了，然后相当于是先把凸包顺序建出来然后查询的时候可以双指针踢队头，取答案总体占一个 \(O(n)\) 级别的跳指针。

细节有点多放个码

#include<bits/stdc++.h>
#define ll long long
#define MAXN 500005 
#define db double
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
int n,q;
ll C[MAXN],X[MAXN];
struct node{
	int v,nxt;
}edge[MAXN];
int h[MAXN],tmp;
inline void add(int u,int v){
	edge[++tmp]=(node){v,h[u]};
	h[u]=tmp;
}
int opt[MAXN],dfn[MAXN],tim;
vector<int>L[MAXN],R[MAXN];
inline void dfs(int u){
	dfn[u]=++tim;
	if(opt[u]>0)L[opt[u]].emplace_back(tim);
	else R[-opt[u]].emplace_back(tim-1);
	for(int i=h[u];i;i=edge[i].nxt){
		int v=edge[i].v;
		dfs(v);
	}
	if(opt[u]>0)R[opt[u]].emplace_back(tim);
	else L[-opt[u]].emplace_back(tim+1);
}
const ll inf=2e18;
inline db slope(int x,int y){
	return (db)((X[x]*X[x]+C[x])-(X[y]*X[y]+C[y]))/(X[x]-X[y]);
}
struct Segment_Tree{
	#define ls(p) p<<1
	#define rs(p) p<<1|1
	#define h(p) tree[p].h
	#define t(p) tree[p].t
	#define sav(p) tree[p].sav
	struct TREE{
		int h,t;
		vector<int>sav;
	}tree[MAXN<<2];	
	inline void build(int l,int r,int p){
		h(p)=0,t(p)=-1;
		if(l==r)return ;
		int mid=l+r>>1;
		build(l,mid,ls(p));
		build(mid+1,r,rs(p));
	}
	inline void modify(int l,int r,int ul,int ur,int id,int p){
	    if(l>=ul&&r<=ur){
	        while(sav(p).size()<=t(p)+5)sav(p).emplace_back(0);
	        if(t(p)>=h(p)&&X[sav(p)[t(p)]]==X[id]){
	            if(C[sav(p)[t(p)]]<=C[id])return ;
	            --t(p);
	        }
	        while(t(p)>h(p)&&slope(sav(p)[t(p)],id)<slope(sav(p)[t(p)],sav(p)[t(p)-1]))--t(p);
	        sav(p)[t(p)+1]=id;++t(p);
	        return ;
	    }
	    int mid=l+r>>1;
	    if(ul<=mid)modify(l,mid,ul,ur,id,ls(p));
	    if(ur>mid)modify(mid+1,r,ul,ur,id,rs(p));
	}
	inline ll query(int l,int r,int x,ll v,int p){
		while(t(p)-h(p)+1>=2&&slope(sav(p)[h(p)],sav(p)[h(p)+1])<=(db)v*2.0)++h(p);
		ll res=inf;
//		printf("p=%lld h=%lld t=%lld\n",p,h(p),t(p));
		if(t(p)-h(p)+1>=1&&sav(p).size())res=(v-X[sav(p)[h(p)]])*(v-X[sav(p)[h(p)]])+C[sav(p)[h(p)]];
		if(l==r)return res;
		int mid=l+r>>1;
		if(x<=mid)res=min(res,query(l,mid,x,v,ls(p)));
		else res=min(res,query(mid+1,r,x,v,rs(p)));
		return res;
	}
}ST;
int idx[MAXN];
inline bool cmp(int x,int y){
	return X[x]<X[y];
}
struct Que{
	ll x;
	int u,id;
	bool operator<(const Que &a)const{
		return x<a.x;
	}
}que[MAXN];
ll ans[MAXN];
signed main(){
	scanf("%d%d%lld",&n,&q,&C[0]);
	for(int i=2,typ,f,idx,_1,_2;i<=n;i++){
		scanf("%d%d%d",&typ,&f,&idx);
		++f;
		add(f,i);
		if(!typ){
			scanf("%lld%d%d%lld",&X[idx],&_1,&_2,&C[idx]);
			opt[i]=idx;
		}
		else opt[i]=-idx;
	}
	for(int i=1;i<=q;i++){
		scanf("%d%lld",&que[i].u,&que[i].x);++que[i].u;
		que[i].id=i;
	}
	dfs(1);
	ST.build(1,n,1);
	for(int i=1;i<=n;i++)idx[i]=i;
	sort(idx+1,idx+1+n,cmp);
	sort(que+1,que+1+q);
	ST.modify(1,n,1,n,0,1);
	for(int i=1,u;i<=n;i++){
		u=idx[i];
//		printf("nowu=%lld\n",u);
		for(int o=0,l,r;o<L[u].size();o++){
			l=L[u][o],r=R[u][o];
//			printf("l=%lld r=%lld\n",l,r);
			if(l>r)continue;
			ST.modify(1,n,l,r,u,1);
		}
	}
	for(int i=1;i<=q;i++)ans[que[i].id]=ST.query(1,n,dfn[que[i].u],que[i].x,1);
	for(int i=1;i<=q;i++)printf("%lld\n",ans[i]);
	return 0;
}

半平面交

板子

~~多边形面积交，考虑用辛普森积分解决。~~

主要用向量相关和凸包解决这个问题。给一个平面向量的封装，cpr就是向量叉积，三个元素就是拿后两个给第一个作差算的，相当于过一交点的线段的叉积。

struct node{
	db x,y;
	node(){}
	node(db a,db b){x=a,y=b;}
	bool operator<(const node &a)const{if(y==a.y)return x<a.x;return y<a.y;}
	bool operator==(const node &a)const{return x==a.x&&y==a.y;}
	node operator-(const node &a)const{return node(x-a.x,y-a.y);}
}sav[MAXN],Cx[MAXN];
inline db cpr(node a,node b){return a.x*b.y-a.y*b.x;}
inline db cpr(node a,node b,node c){return cpr(b-a,c-a);}

极角排序

可以用 atan2(y,x) 求得 \(\vec a=(x,y)\) 关于 \(x\) 轴夹角的弧度。考虑对所有多边形的边计算出极角并从小到大排序。

排好序之后对贡献的向量只保留最靠近可行域的那个，半平面交最后会是一个凸多边形的形式，进而考虑对保留下来的向量和交点维护凸包。

具体地维护有以下情况：

比如说现在逐个加入 \(\vec a,\vec b,\vec c\)，加入 \(\vec c\) 的时候发现上一个交点 \(D\) 在当前半平面交的另一侧，那说明 \(D\) 和 \(\vec b\) 可以扔掉了。

然后闭合凸包的时候

后来的向量可能会踢掉最开始若干个点和向量，总之就是实现一个双端队列就能维护。

闭合之后还得用队首踢一下队尾，因为队尾还没限制。

板题里边让你求面积，搓出来之后三角剖分一下就好了。

题：学校oj上没人做这块，我直接把写的题解抄过来了。

赛车

对于正解：车 \(i\) 于 \(t\) 时刻的位移是 \(x_i+tv_i\)，能作为队头当且仅当存在一个时刻 \(t_0\) 使得 \(\forall j\neq i,x_i+t_0v_i>x_j+t_0v_j\)，把这些一次函数放到平面上，则 \(i\) 应当作为第一象限内半平面交凸壳的一部分。

考虑更简单的做法：由于 \(n\le 10^4\)，\(O(n^2)\) 解不等式判断是否存在一个 \(T_i=[L_i,R_i]\) 使得其位移大于其他车即可。

铁人三项（Saber vs Lancer）

设给定三个速度为 \(v_1,v_2,v_3\)，三段路程为 \(x,y,1-x-y\)。

钦定一个 \(i\) 为胜者当且仅当满足

\[\nexists j\neq i,v_{1,2,3,i}\le v_{1,2,3,j},\\\forall j \neq i,x(\frac{1}{v_{1,i}}-\frac{1}{v_{1,j}})+y(\frac{1}{v_{2,i}}-\frac{1}{v_{2,j}})+(1-x-y)(\frac{1}{v_{3,i}}-\frac{1}{v_{3,j}})<0 \]

考虑将 \(v\) 相关计算看成常数并整理为 \(Ax+By+C<0\) 的形式，拆完分讨一下 \(B\) 正负,半平面交判有无解即可。

另外 \(x,y\) 由定义天然满足 \(x>0,y>0,1-x-y>0\)。

逃考

首先，样例中第二个输入有误，出现了一个边界外的亲戚。

其次，小杨可以没有亲戚。

Voronoi 图由一组由连接两邻点直线的垂直平分线组成的连续多边形组成，根据 \(n\) 个在平面上不重合种子点，把平面分成 \(n\) 个区域，使得每个区域内的点到它所在区域的种子点的距离比到其它区域种子点的距离近。

亲戚的管辖范围形成了 Voronoi图。进一步地，如果对 Voronoi图上接壤的亲戚连边，对和边界接壤的亲戚连接到汇点就可以用最短路解决这个问题。

考虑如何判断亲戚二元组 \((i,j)\) 在 Voronoi图上接壤。根据定义，图上接壤节点间的分界线应当是两点间的垂直平分线，显然对于 \(i\) 管辖区域的中垂线边集应当是它与其他所有点中垂线边集的一个子集，再看就应当是这个大边集的半平面交。\((i,j)\) 接壤当且仅当 \((i,j)\) 对应的中垂线在 \(i,j\) 两点对应的凸包上。

所以维护每个亲戚与其他亲戚连线中垂线的半平面交并对每个边备注所属的亲戚编号方便后续建图，半平面交部分的复杂度是 \(O(n^2logn)\)，瓶颈在排序。

小凸想跑步

想一下应该就是：点 \(P\) 的可行面积/总面积，后者可以直接三角剖分，考虑如何确定前者。

假设p01的三角形为 \(PAB\)，某个三角形为 \(PCD\) 则 \(\forall C,D\) 应有：

\[\overrightarrow{BP}\times\overrightarrow{BA}<\overrightarrow{CP}\times\overrightarrow{CD} \]

\[(x_P-x_B,y_P-y_B)\times(x_A-x_B,y_A-y_B)<(x_P-x_C,y_P-y_C)\times(x_D-x_C,y_D-y_C) \]

\[(x_P-x_B)(y_A-y_B)-(y_P-y_B)(x_A-x_B)<(x_P-x_C)(y_D-y_C)-(y_P-y_C)(x_D-x_C) \]

\[(y_A-y_B)x_P-y_P(x_A-x_B)+y_B(x_A-x_B)-x_B(y_A-y_B)<(y_D-y_C)x_P-x_C(y_D-y_C)-(x_D-x_C)y_P+y_C(x_D-x_C) \]

\[(y_A-y_B+y_C-y_D)x_P+(x_B-x_A+x_D-x_C)y_P+x_Ay_B-x_By_A+x_Cy_D-y_Cx_D<0 \]

设

\[A=(y_A-y_B)+(y_C-y_D)\\ B=(x_B-x_A)+(x_D-x_C)\\ C=\vec{A}\times\vec{B}+\vec{C}\times\vec{D}\\ Ax_P+By_P+C<0 \]

原来写这个式子的草纸没了，这个是现敲的，可能会错但是反正就是那么个一次函数线性规划的形式，你自己推一下得了嘻嘻。

然后你算一下相邻点的横纵坐标差拿推出来的式子跑一下半平面交，记得把原多边形也塞进去跑半平面交，理论上这样跑完三角剖分求面积作比就完事了。

但是这个题被卡精也是不可不品鉴的一环嘻嘻，数据我已经让教练帮忙搞到文件里了你自己拍拍乐吧然后提供一些可能有用的注意事项。

第一次见到神人题精度开高会死的，如果你eps在1e-9以下得30/70pts试一下把eps换成1e-8，1e-7这一类，之前开1e-14发现极角排序没有相同斜率直线结果凸包里一堆平行线呃呃。
这个题的向量很容易有横线竖线可以用点+斜率的方式表示向量。
不过要硬用两点表示向量也是ok的你拿着式子注意一下 \(B\) 是不是快为0是的话就是一个 \(Ax+C<0\) 的形式按 \(A\) 正负分讨就行。

Poi2009 Wsp-island

显然可以把 \(O(n^2)\) 条可行路径扒出来跑一个半平面交，这样得到的凸壳就是最短路，但是会炸，考虑有没有什么简化的方法。

发现给出的图是一个凸多边形，所以越是靠近 \(n\) 的点越有用，而且编号大的点严格有用于编号小的，你记录一下每个点不能连的点然后从 \(n\) 到 \(1\) 找第一个它能连的点，这样边数就是 \(O(n)\) 的了。

最后把 \((1,n)\) 一连跑个半平面交算凸包周长减掉 \((1,n)\) 距离即可。

posted @ 2025-01-20 19:44 Cl41Mi5deeD 阅读(66) 评论(0) 收藏举报

刷新页面返回顶部

Claimo0611

......