后缀数组 manacher 回文自动机 后缀自动机
后缀数组
后缀数组可以把字符串的所有后缀存起来,然后干各种奇怪的事情。
现在给你一个字符串 banana,给他的后缀A,NA,ANA,NANA,ANANA,BANANA
跑一个后缀的trie。
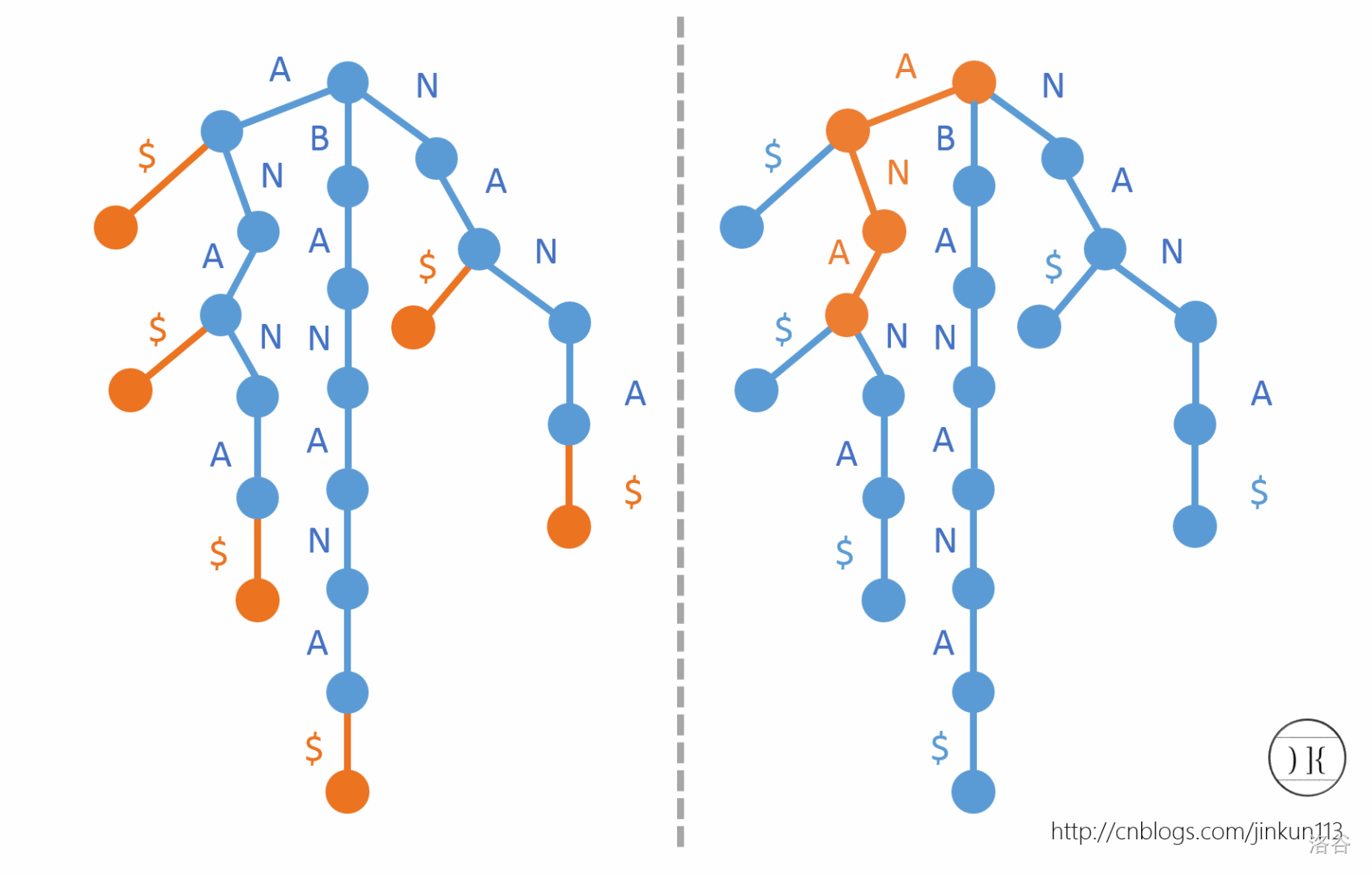
然后把字典序小的字母排在左边,给每个后缀对应的叶节点标一下这个后缀首字母在文本串的位置。
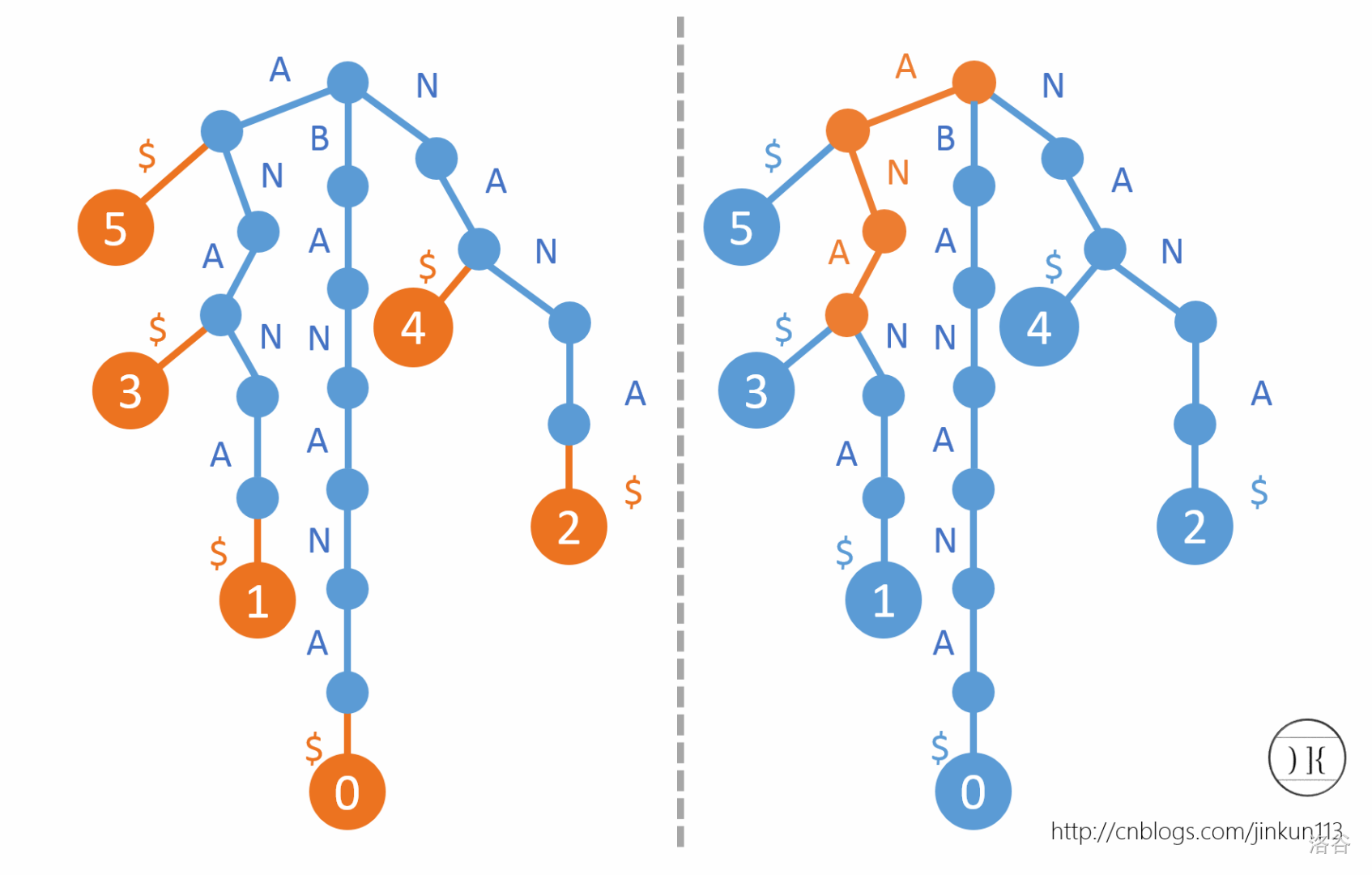
从左到右连接下标就是后缀数组,比如这个的后缀数组是 \(5,3,1,0,4,2\)。实际意义:sa[1]=3 表示第3+1=4个字母开头的后缀 ANA 在所有后缀中的字典序为1,sa[3]=0 就是 BANANA 的字典序为3。
int cnt[MAXN],lsa[MAXN],lrk[MAXN];
int sa[MAXN],rk[MAXN],hei[MAXN];
void getSA(){
m=128;
for(int i=1;i<=n;i++)cnt[rk[i]=txt[i]]++;
for(int i=1;i<=m;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--)sa[cnt[rk[i]]--]=i;
int p=0;
for(int k=1;k<n;k<<=1,m=p){
int cur=0;
for(int i=n-k+1;i<=n;i++)lsa[++cur]=i;
for(int i=1;i<=n;i++)if(sa[i]>k)lsa[++cur]=sa[i]-k;
memset(cnt,0,sizeof cnt);
for(int i=1;i<=n;i++)cnt[rk[lsa[i]]]++;
for(int i=1;i<=m;i++)cnt[i] += cnt[i-1];
for(int i=n;i>=1;i--)sa[cnt[rk[lsa[i]]]--]=lsa[i];
for(int i=1;i<=n;i++)lrk[i]=rk[i];
p=0;
for(int i=1;i<=n;i++){
if(lrk[sa[i]]==lrk[sa[i-1]] && lrk[sa[i]+k]==lrk[sa[i-1]+k])rk[sa[i]]=p;
else rk[sa[i]]=++p;
}
}
}
inline void getH(){
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1)continue;
if(k)--k;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&txt[i+k]==txt[j+k])++k;
hei[rk[i]]=k;
}
}
板题代码。
相当于给后缀拼上前缀排序,我们可以直接给字符串扩一倍复制一下拿新的后缀跑后缀排序,找前 \(n\) 位的后缀数组输出即可。
这个要涉及到SA的一种用法叫最长公共前缀。用 \(height_i\) 表示 \(sa_{i-1}\) 和 \(sa_i\) 的最长公共前缀长度。令 \(j,k\) 为两个前缀,\(jj<k,rank_j<rank_k\),则 \(j,k\) 的lcp 长度 \(min\{ height_{rank[j+x],x\in[1,k-j]}\}\)
。
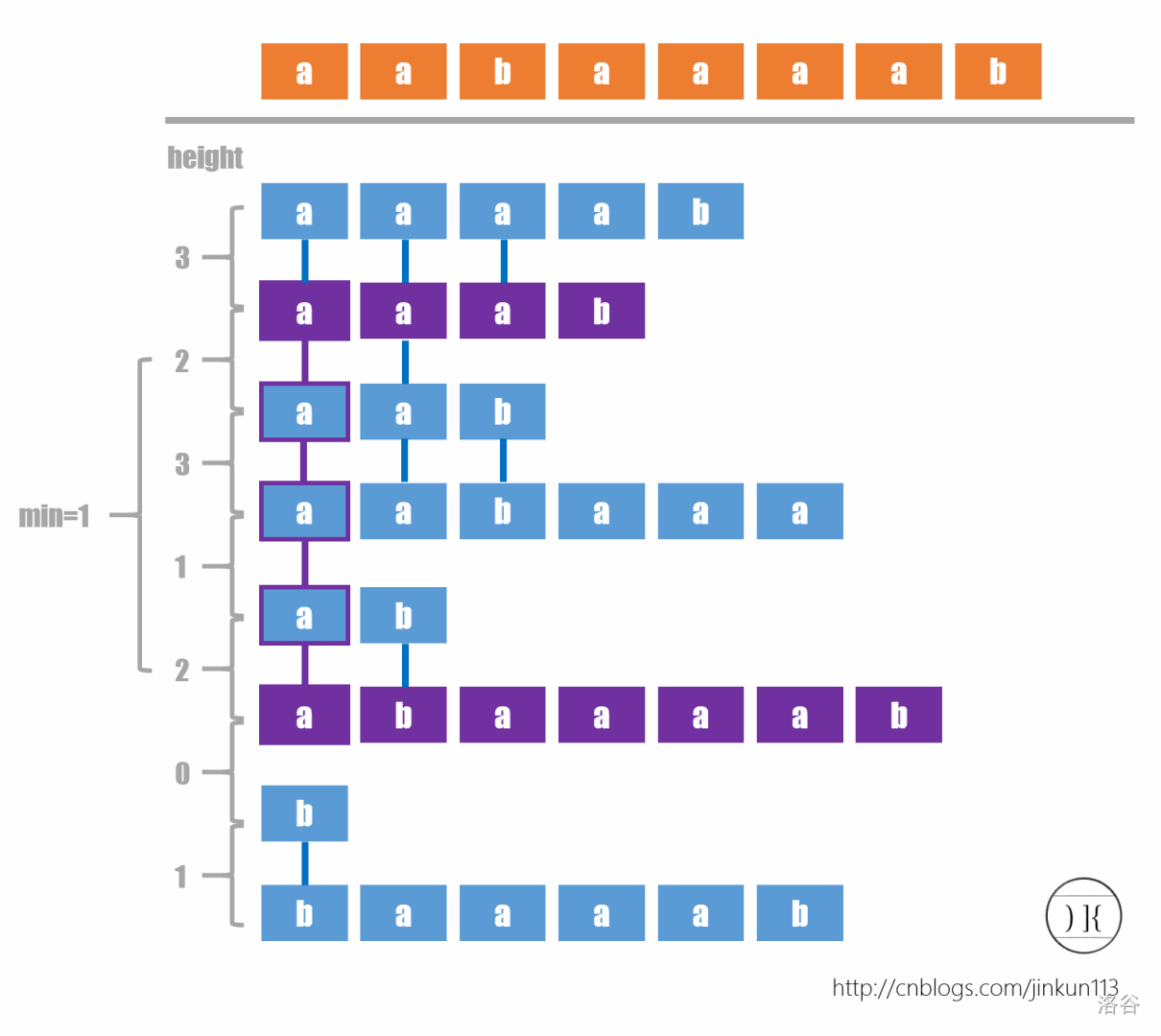
这个就非常牛逼了。上面的码已经写了怎么求这个数组。
在本题中对于排好序的两个后缀他俩的 \(height\) 即后缀的最长公共前缀长度可以反映出他俩间贡献的相同子串个数,如图中后缀 aaaab 和 aaab 的 \(height=3\),则有 a,aa,aaa 三个相同子串。
\(Ans=n+\binom{2}{n}-\sum height_i\)
Que:求一个字符串的最长回文串长度。
提出技巧:在原串后加入一个分隔符 {,在复制一份颠倒的字符串拼接到后面跑后缀数组。
进而一旦出现回文串就一定存在一个原串部分的后缀和一个新串部分的后缀有 LCP,取height最大值即可。
对刚才那个技巧的延伸。
可以把所有串拼成一个大串,分隔符就是 '{'+i,加是因为分隔符一样会影响后缀排序。
从 \(height\) 上考虑这个问题,相当于找到一个 \(height\) 连续段,这个段上的后缀恰好在每个原串中都有分布,现在求出每个合法段的 \(max\{min_{i=l}^r height_i\}\)。根据答案分布希望合法段越短越好,就可以用双指针维护区间,右边塞左边删到不能删之后与 \(height\) 区间上取极值,用rmq解决。
和上一道题是一样的,界定相同串的规则变成了差值相同,维护查分数组的SA即可,最后答案+1。
长的很ac自动机的一道题,但是我不会ac机。
先按套路把文本串赋id后拼长串跑SA。可以发现对于一次点名可以二分找出后缀序列中字典序和模式串满足权值偏序的转折点,进而考虑对模式串 \(p\) 找大于等于的后缀位置 \(L\) 和大于的后缀位置 \(R\),区间 \([L,R]\) 内的后缀一定包含 \(p\)。
进而问题一转化成处理后的区间 \([L,R]\) 内的 \(id\) 数,可以用莫队解决。问题二则可以在莫队添删元素的时候维护。添删的时候加减上之后的询问数即可。
在 \(\binom{2}{n}\) 个子串中每个后缀会被加 \(n-1\) 次。问题简化为求全后缀对LCP之和。
序列上的全点对问题极值可以用单调栈的套路处理,就是维护每个后缀成为答案贡献点的最长左右延伸,判定用 \(<\) 而不是 \(\le\) 不然要算重。
manacher
不难。板子思路就是维护当前最右侧的一段回文串 \([l,r]\),每次新加一个字符看一下在不在那个回文串里在的话就把它在回文串里的对称点答案继承一下但是这个答案可能比较大大过 \(r-i+1\) 的话 \(r\) 右侧是不确定的所以把这两数取最小,取完在已有基础上暴力扩张。题目普遍比较一眼就不放了。
PAM
没学过ac自动机,略微吃力不过板子还是不难的。
就是先建trie树(稍微改造一下成回文版)然后建fail。每次新加一个字符会形成若干新回文串,考虑最长的那个回文串中一定包含了较短的那些新回文串(画图理解)而且较短的那些一定先前被存过了所以本质不同回文串是 \(O(n)\) 的。考虑用trie树节点记录这些本质不同回文串,然后建立fail,记录一下当前回文串的最长回文后缀,这个后缀是肯定出现过的,这个后缀在trie树上的所在节点就是fail所连的点。
SAM
我该怎么描述这个东西。。
就是说,在 \(O(nlogn),O(n)\) 的时空复杂度下搓一个自动机,然后从原点出发的任一路径就是原串的一个子串。然后这个东西是由 转移边next(一个dag) 和 后缀链接形成的parent树 组成的。这两个图状物共用 \(O(n)\) 个节点(状态)。满足一些牛逼的性质,先说转移边dag,原点出发的路径值得就是这个dag而不是parent树上的路径,状态 \(u\) 用一条 \(c\) 字符转移边连接到 \(v\) 当且仅当两者代表的字符串满足 \(str_u+c=str_v\)。
那显然这个dag应该会比较多且丑,考虑用一种方案让这个dag变得好看就是parent树和后缀链接,就是把一个子串的所有结束位置称作它的 \(endpos\) 集合,会有一些子串的这个集合是相同的,不难发现一长一短的两个子串uv满足这样的关系当且仅当v是u的后缀且仅为后缀(要不然v的endpos应该包含u的,就拿来搓parent树的说),然后endpos相等的这一堆子串叫等价类,满足一个等价类里最短和最长长度子串中间的这些长度都有这个等价类里的子串覆盖。然后再说后缀链接就是从一个等价类的最长的那个子串连到另一个等价类用的。具体而言因为要保证endpos相等所以等价类最长串 \(u\) 的并非所有后缀都会和它在一个等价类里,第一个不在它等价类的它的后缀就是 \(u\) 要后缀链接到的状态,那不出意外满足 \(endpos_u\) 里的最短子串 \(v\) 和第一个不在它等价类的 \(u\) 后缀 \(w\) 满足 \(len_v=len_u+1\)。
然后关于怎么搓,就是说对每个状态存它的最长的那个子串 \(len\),那很明显逐个加字符的时候 \(len\) 应该是递增的,然后每次从上次往它的link跳看看能不能加一个字符变成当前这个状态能的话就连dag边。然后先回家了。然后从第一个没法连dag边的状态开始之后的fa也没法连了,看一下这个时候是否满足 \(len_v=len_u+1\) 满足的话就连后缀链接。不满足就比较蛋疼就是说 \(v\) 应该只满足 \(len_v\ge len_u+1\) 所以不等一定是大于的然后从 \(v\) 里面分出来一个clone \(w\) 满足 \(len_w=len_u+1\),然后把所有 \(v\) 的相关copy到 \(w\) 上,最后把 \(cur\) 和 \(v\) 都链接到 \(w\) 上就行了。
然后说parent树就是把每次插入形成的字符串(即文本串的前缀)对应状态叫终点那parent树上的点的 终点集合和他子树内的终点节点的集合是相等的。然后 \(str_{1..x}\) 和 \(str_{1..y}\) 的lcs是parent树上俩人的lca。然后满足树上一个节点的子串数量等于 \(len_u-len_{fa_u}\)
然后再说一下广义后缀自动机,有一种很好用的假做法是拿一个文本串建一个一般的sam然后后面的文本串每次清空last继续建,这样正确性是对的但是时空没有标准的优。然后我用的是tj区里的在线做法,就是说在这种假作法上加一些特判,我没太明白但是会敲。因为短。以后看懂了再记。
#include<bits/stdc++.h>
#define MAXN 1000005
#define ll long long
using namespace std;
int m,n;
ll ans;
char txt[MAXN];
struct Suffix_Automaton{
int tot=1,pos[MAXN<<1];
int fa[MAXN<<1],len[MAXN<<1],nxt[MAXN<<1][26];
inline int insert(int c,int lst){
if(nxt[lst][c]&&len[nxt[lst][c]]==len[lst]+1)return nxt[lst][c];
int cur=++tot,p=lst,f=0;
len[cur]=len[lst]+1;
while(p&&!nxt[p][c])nxt[p][c]=cur,p=fa[p];
if(!p){fa[cur]=1;return cur;}
else{
int q=nxt[p][c];
if(len[q]==len[p]+1){fa[cur]=q;return cur;}
if(p==lst)f=1,cur=0,--tot;
int cl=++tot;
len[cl]=len[p]+1;
fa[cl]=fa[q],fa[q]=fa[cur]=cl;
for(int i=0;i<26;i++)nxt[cl][i]=nxt[q][i];
while(nxt[p][c]==q)nxt[p][c]=cl,p=fa[p];
return f?cl:cur;
}
}
}SAM;
#define pos SAM.pos
#define nxt SAM.nxt
#define fa SAM.fa
#define len SAM.len
signed main(){
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%s",txt+1);
n=strlen(txt+1);
pos[0]=1;
for(int j=1;j<=n;j++)pos[j]=SAM.insert(txt[j]-'a',pos[j-1]);
}
for(int i=2;i<=SAM.tot;i++)ans+=(ll)(len[i]-len[fa[i]]);
printf("%lld\n%d",ans,SAM.tot);
return 0;
}
板子题大概就是这么个东西。然后整理一下题。
拿parent树定义说话就是说当前等价类的到它后缀链接最长长度之间的这一段子串肯定都是有的,每次的贡献就是 \(len_i-len_{fa_i}\)。
这题用SA早秒了。。
可以重的话,树上一个点的出现次数就是它子树出现次数之和,跑treedp,要不然直接全给成1。然后求的是第k小,在dag上贪心从小到大选,减去贡献并统计答案,可以记忆化一下。
这种题sa,sam,广义sam都能做。
sam做法其实是伪广义sam的一种实现,说一下就是上面提到的那种假做法,先跑第一个文本串,后面的当模式串一个一个在文本串上匹配,每次记录一个 \(sav_u\) 表示到parent树节点 \(u\) 的最长匹配长度,然后儿子的答案是能贡献到父亲的就是说 \(sav_f=max(sav_f,min(len_v,sav_u))\)(因为贡献的答案肯定不能超过fa的len啊),单次答案算完之后汇总到总答案 \(ans_u\) 上,总答案要对单次答案取最小(显然啊)最后对 \(ans_u\) 取最大。
sandy卡片跑个差分预处理就行,没啥说的。
看到了一种不拆式子直接算的方法,就是说答案形式很想一个parent树上lca的形式,所以直接求parent树上全点对路径和即 \(\sum_usiz_u(n-siz_u)(len_u-len_{fa})\)。用 \(n\) 不用 \(tot\) 是因为有 \(siz\) 的只有 \(n\) 个点。
显然从所有叶子出发跑完所有路径就是答案,而且叶子还只有20个,然后就写广义SAM,每次从它的 \(fa\) 当lst继承。
不是很难。就是说二分答案然后 dp 验证一下,设 \(dp_i\) 表示到 \(i\) 能匹配的最多数。
然后那个 \(maxmatch(i)\) 就是说拿第 \(i\) 位结尾最多匹配到多少文本串,拿文本串建一个广义sam然后跑匹配可以 \(O(n)\) 求。
瓶颈在dp,然后发现 \(i-maxmatch(i)\) 这个玩意后面的部分增量最大就 1(废话)所以是单调的,区间右端点显然是单调的,写个单队dp。
就是说,求一下文本串的 sam,一个询问问的就是段区间内 parent树 上若干个点中 lca 对应 \(len\) 最大的那个点对。
一个套路是把询问按右端点离线了,然后每次对于一个节点扫一下不同的枝杈,枝杈间点的lca肯定是这个点 \(u\),贡献也就是 \(len_u\),然后考虑拿若干 set 跑启发式合并,因为贡献要尽可能多给所以每次新引进一个贡献 \(v\) 就直接在 \(u\) 的 set 里找它的前驱后继,这样贡献的区间就尽可能窄了,就能最优化。
合并完就会得到若干三元组 \((l,r,len)\) 表示在询问区间 \([l,r]\) 上有 \(len\) 的贡献。给这些三元组也按右端点排个序跑个二维数点就好了。复杂度是 \(O(nlog^2n)\) 的。
就是说和上个题是一样的,给文本串倒过来搓sam,然后处理一下异或,又因为想和上一题一样用启发式合并所以学了一下01trie合并。复杂度 \(O(nlog^2n)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号