搬luogu的文章之近期进度小结
一亿年前写的,忘挪了。
推到淀粉质才发现前面好多都没总结过,怕掺水就提两句。
不过现在确实发现不用写那么详细,又不是给别人看。
基环树
基环树就不提了,手玩样例该咋做咋就就可以,大多是细节题没什么技巧。
笛卡尔树
这个东西很抽象,这里说一下定义。
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 (k,w) 构成。要求 k 满足二叉搜索树的性质,而 w 满足堆的性质。一个有趣的事实是,如果笛卡尔树的 k,w 键值确定,且 k 互不相同,w 互不相同,那么这个笛卡尔树的结构是唯一的。

与其他数据结构不同,在我看来这个东西是题目"模型正好满足笛卡尔树"才去使用,而不是"考虑用笛卡尔树维护",换句话说就是使用范畴很抽象,考场上真出了很难想到并做出来。
制作这种结构的平衡树可以用维护右链的方式 \(O(n)\) 构造。
stac[1]=1;
for(int i=2;i<=n;i++){
while(a[stac[top]]>a[i]&&top)--top;
if(!top)ls[i]=stac[top+1];
else ls[i]=rs[stac[top]],rs[stac[top]]=i;
stac[++top]=i;
}
方法和虚树是类似的,不过这个更简单。
这两道题分别展示了笛卡尔树键值的作用,翻转键值可以使你的笛卡尔树解决一些很骚的问题。
笛卡尔树可以反应数据的函数形式,具体的可以把数据的导数和端点值大小关系反映出来。
一种形状的数据的笛卡尔树是唯一的,本题中就运用到了这个技巧。
显然这个相似序列的定义就是每一位在序列中的大小与模版序列一致。进而他俩的笛卡尔树是一致的。
现在问你 \([0,1]\) 内的实数序列与模版序列相似的期望权值。既然是实数,那么期望值就是 0.5,我半天没反应过来。
既然要求笛卡尔树同构,那么给出笛卡尔树每个节点的字数大小 \(siz_i\)。可知同构的概率就是 \(\frac{1}{\Pi siz_u}\)。乘起来就行。
这个题思路是真的叼,dyc能自己想出来,令人感叹。
观察(颓题解)得,这个不完全的矩阵可以构造成一棵笛卡尔树。
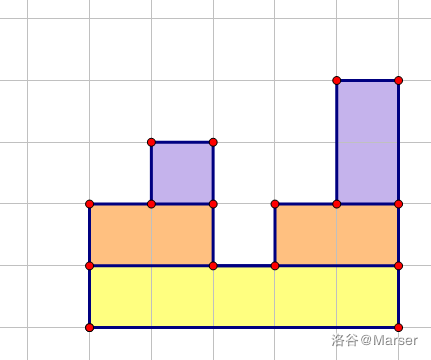
我们发现,这样构成的若干个矩形正好对应小根笛卡尔树上的所有节点,每次递归处理的两个小联通块正是当前节点的两个儿子。根据定义,我们可以知道,对于节点
$x $ 代表的矩形,它的长度为\(siz_x\),高度为 \(h_x−h_{fax}\)。
建好笛卡尔树后在笛卡尔树上进行树形dp,相当于每个节点形成的小矩阵的节点都应该行列没有共点,父节点的子节点会占用它宽度的列数导致不能放。
然后dp。\(dp_{i,j}\) 为 \(i\) 的子树放 \(j\) 个元素的方案数。假设当前节点放了 \(j\) 个,剩下子树中的节点放了 \(k\) 个,那么此矩阵的方案为 \(C_{siz_u-k}^jC^j_{h_u-h_{fa}}*j!\)。
最后合并即可。
这个题倒是简单,发现老鼠洞形成了一棵笛卡尔树,造好之后跑一遍欧拉序生成01串,然后hash。
还有一题我纯颓的,没脸放这了。
扫描线
就是用线段树解决计算几何问题。
如何处理平面内一群矩形的面积交?
考虑用面积的朴素定义,\(S=ab\),相当于一堆面积合到一起就是 \(b\) 个可以不同的 \(a\) 相加。
我们维护坐标系的 \(x\) 值,再去跳 \(y\) 轴。具体地,只有一个矩形的下边界和上边界才会对当前 \(x\),也就是 \(a\) 值之和造成影响。我们记录一下矩形的上下底面,在下底面 \(y\) 值加上它覆盖的 \(x\) 段,在它的上底面减去它的 \(x\) 段,按照 \(y\) 给这些操作排序后去跳 \(y\),该加加改减减。线段树维护当前 \(y\) 内的 \(x\) 之和,相当于会形成很多的长度段,一堆叠在一起也算一个,瞎搞一下维护即可,\(S=\sum \Delta y*x_i\)。
放个代码方便复习。
#include<bits/stdc++.h>
#define MAXN 1000005
#define int long long
using namespace std;
int n;
struct node{
int x1,x2,y;
int opt;
}sq[MAXN<<1];
inline bool cmp(node a,node b){
if(a.y==b.y)return a.opt>b.opt;
return a.y<b.y;
}
int mp[MAXN<<2];
int ans,tmp;
struct Segment_Tree{
#define ls(p) p<<1
#define rs(p) p<<1|1
struct TREE{
int l,r;
int val,tag;//维护一个当前x段的覆盖层数和贡献,只要有层数就有贡献,没层数就没贡献
}tree[MAXN<<3];
inline void build(int l,int r,int p){
tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].tag=0;
if(l==r)return;
int mid=l+r>>1;
build(l,mid,ls(p));
build(mid+1,r,rs(p));
}
inline void push_up(int p){//主要看看pushup即可
if(tree[p].tag)tree[p].val=mp[tree[p].r+1]-mp[tree[p].l];
else{
tree[p].val=tree[ls(p)].val+tree[rs(p)].val;
}
}
inline void modify(int l,int r,int k,int p){
if(mp[tree[p].r+1]<=l||mp[tree[p].l]>=r)return;
if(mp[tree[p].l]>=l&&mp[tree[p].r+1]<=r){
tree[p].tag+=k;
push_up(p);
return;
}
// printf("nowmid=%lld,id=%lld,tree.l=%lld,tree.r=%lld\n",mid,p,tree[p].l,tree[p].r);
modify(l,r,k,ls(p));
modify(l,r,k,rs(p));
push_up(p);
}
}ST;
signed main(){
scanf("%lld",&n);
for(int i=1,x1,x2,y1,y2;i<=n;i++){
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
sq[i]=(node){x1,x2,y1,1};
sq[i+n]=(node){x1,x2,y2,-1};
mp[i]=x1,mp[i+n]=x2;
}
sort(mp+1,mp+1+n*2);
tmp=unique(mp+1,mp+1+2*n)-mp-1;
//printf("tmp=%lld\n",tmp);
sort(sq+1,sq+1+n*2,cmp);
ST.build(1,tmp-1,1);
//printf("ced\n");
for(int i=1;i<n*2;i++){
// printf("solving %lld %lld %lldf\n",sq[i].x1,sq[i].x2,sq[i].opt);
ST.modify(sq[i].x1,sq[i].x2,sq[i].opt,1);
ans+=ST.tree[1].val*(sq[i+1].y-sq[i].y);
}
printf("%lld",ans);
return 0;
}
现在让你计算那坨矩形的周长。
同样的分析方法,矩形的下底面和上底面都会对当前答案做出贡献,但是贡献是 \(\Delta x\),相当于新增的或新减少 x 的才是当前 \(y\) 的 \(x\) 贡献,自己画个图想去。
然后考虑竖条对答案的贡献,当前线段树覆盖的一堆线段会形成许多个分开的块,具象下来就是当前 \(y\) 区段实际参与计算的矩形个数。
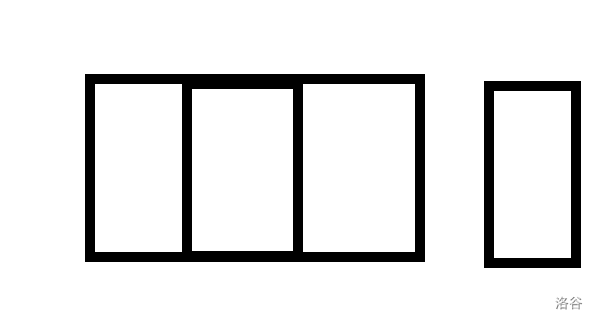
像是这张图虽然有三个矩形但只形成了两个块,因此实际的竖条个数是当前块数(2)乘以2。
用线段树再维护一下当前区段是否充满就可以推出来一共有几个块,满了就不加,不满就块数相加。
考虑用扫描线解决。
用矩形框点太蛋疼了,把点变成框那么大的矩形再用扫描线处理。
每个矩形相当于可以提供它权值的贡献,把这些贡献在 \(x\) 上叠加,发现线段树的极值就是当前 \(y\) 窗口能覆盖到的最大星星权值。没了。
虚树
怎么建树之前写过了,讲一讲题目思路吧。
虚树是一种优化手段,但不代表你得像鞋油那样先推朴素式子在优化。
甚至很多时候都是需要先用虚树把关键点抽象出来才能比较舒服的dp的。
像切断一个节点领导的子树有以下方法:
- 切断他所有儿子领导的子树
- 切断他自己的父亲与他的联系
\(dp_u=min\{\sum dp_{son},min\{e,e\in V_{fa->u}\}\}\)
跑虚树,预处理切断父亲的最小边后 dp 即可。
有个傻逼一看题就想到正解结果因为把题面看错了揣着正解看了半天不会做。
那个傻逼是我,我没看见它还要回去,一直想着怎么保证最小联通子树砍掉一遍路径能完整且最短。
事实上要是回去的话答案就是最小联通子树。
把最小联通子树的虚树跑出来。按dfn看相当于当前点和他在目标序列中的前驱后继求距离和。增加一个点就把他插入序列,更新答案,删除同理。增删且前后继+路径权值,直接对他使用平衡树+树剖生成300行恶臭代码,你就说过没过吧。
跑个虚树,考虑路径和:每条边将虚树分割为 \(siz\) 和 \(tot-siz\) 个关键点的两个联通块,那么这个边会被经过他俩的积次,造成 \(val*siz*(tot-siz)\) 的答案贡献。
按照贪心原则,树上最长链一定经过叶子即关键点,不用怕跑到lca上就不跑了。维护一个最长链和次长链,统计这个节点的儿子,有多个儿子就相加,没有就取最长。
最短路径可不是最短边,你得强制他经过两个叶子,维护到叶子的最短链和次短链,给一点细节让他必须经过叶子就行。
这道题我把题解发到学校oj上了,这个是链接。
还有一道世界树,自己推了半天发现和tj完全不沾边,有点小崩,先不写这个了。
主席树
本来想写的就是主席树小结,结果写到这剩三分钟放学,我呃呃。
教你如何实现可持久化,这种先建全树后修改的结构不会出现在接下来的任何一道题中,就因为这个坑了lz半天没明白主席树是想干啥。
主席树可以理解为对区间信息的前缀和,如果信息可以通过一定方法相减的话。(这已经揭示主席树除了前缀和查区间信息还可树套树改区间元素)。
因为可持久化线段树每多一个版本只需要新建 \(O(log)\) 的节点,所以我们可以开 \(n\) 棵权值主席树维护 \([1,1],[1,2]...[1,n]\) 这样一坨前缀区间的权值树,权值树查kth很舒服。那么查询区间 \(kth\) 时,我们把第 \(r\) 版本的线段树和 \(l-1\) 版本的线段树的元素个数相减,在这个区间内进行跳 kth 的操作。当前元素差值个数 \(v\) 小于 \(k\) 时让两棵树一起跳跳右子树再查,否则就左子树。
注意到模式串长度固定,预处理每位引导的hash然后对它建权值主席树,每次在第 \(r->l-1\) 版本的树作差找权值就行了。
这个题可以莫队。
这个题有一种经典的处理方法,后面也会用。
维护一个 \(lst_{col}\) 数组表示颜色 \(col\) 上次出现的位置,按每一位建主席树的时候先copy上个版本,给这个版本这一位置的颜色+1,然后给这个版本于该位颜色的上次出现位置-1,这样第 \(i\) 棵主席树就解决了区间 \([1,i]\) 的同颜色答案重复问题。
查询 \([l,r]\) 时因为我们这次是下标而非权值主席树,在第 \(r\) 版本的主席树中查询 \([l,r]\) (其实 \([l,n]\) 也行因为这棵树后面没更新)的权值和即为答案。
如何在树上查询路径中的第 \(k\) 小权值?
考虑主席树的基本原理即前缀和(差分),既然序列上的静态问题可以用前缀和思想解决,那么树上的静态问题也是同理。
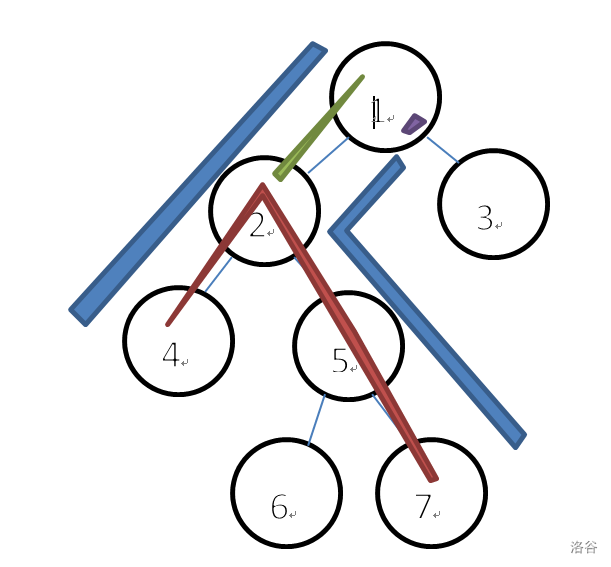
比如求路径和,那么可以预处理点到根节点的距离 \(dis_u\),可知两点的距离 \(dis(x,y)=dis_x+dis_y-dis_{lca}-dis_{fa_{lca}}\)。
同理地我们从根节点往下按dfn建权值主席树,那么点对 \((x,y)\) 的信息就这么作差:\(ans=rt_x+rt_y-rt_{lca}-rt_{fa_{lca}}\)
维护 \(x,y,lca,flca,l,r,k\) 六个信息跑权值主席树。
inline void modify(int l,int r,int x,int pre,int &p){
p=++tot;
tree[p]=tree[pre];
++tree[p].val;
int mid=l+r>>1;
if(l==r)return;
if(x<=mid)modify(l,mid,x,ls(pre),ls(p));
else modify(mid+1,r,x,rs(pre),rs(p));
}
inline int query(int l,int r,int lx,int rx,int lcax,int fx,int k){
int mid=l+r>>1;
if(l==r)return l;
int v=tree[ls(rx)].val+tree[ls(lx)].val-tree[ls(lcax)].val-tree[ls(fx)].val;
if(v>=k)return query(l,mid,ls(lx),ls(rx),ls(lcax),ls(fx),k);
else return query(mid+1,r,rs(lx),rs(rx),rs(lcax),rs(fx),k-v);
}
跳左右儿子的过程直观不好想,感性理解吧。
这里提一嘴启发式合并。
这个东西听起来就特别潮,一搜全是紫题,其实就是一个猪鼻优化。
别名 dsu on tree,树上并查集(雾,相似地,维护散点所属集团的根节点,比对合并。
最开始每个点的首领是他自己,每次找到两个点时,找到较小 (siz) 的那个集团然后直接暴力把小树插在大树上,对就是再对小树跑一遍 dfs 重新汇总答案。看起来是 \(O(n^2)\) 的,不过因为一些轻重链和势能问题,最后的复杂度是 \(O(nlog n)\) 的。证明网上有。
好现在看这道题。
如果没有 L 操作那么这道题就是上面的板题。现在考虑合并。既然建树的过程就是按树的结构造主席树,那每次合并就嗯和,连边,然后合并父亲,然后直接再建一次主席树。
inline void dfs(int u,int fa,int col){
vis[u]=col;
lcafa[0][u]=fa;
ST.modify(1,cnt,Val[u],ST.rt[fa],ST.rt[u]);
for(int i=1;i<=20;i++)lcafa[i][u]=lcafa[i-1][lcafa[i-1][u]];
dep[u]=dep[fa]+1;
siz[u]=1;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v;
if(v==fa)continue;
dfs(v,u,col);
siz[u]+=siz[v];
}
}
...
if(opt[1]=='L'){
int fx=getf(x),fy=getf(y);
if(siz[fx]<siz[fy])swap(x,y),swap(fx,fy);
dfs(y,x,vis[x]);
siz[x]+=siz[y];
add(x,y);
add(y,x);
}
然后就好了。时间复杂度 \(O(nlog^2n)\)。
好多好玩的题都在bzoj上,谷没有水不了通过
这里复习一下我学成史的数论知识。
发现区间中这个 \(n\) 比较大,那就得从质因子入手了。
eulerphi 中质因子是不能重复算的,相当于要求这个区间中有去重后质因子之积。
这不就是颜色序列那道题嘛!维护每个质因子上次出现的位置,主席树中的权值改成积之值,然后就可以过了。
最开始感觉像是区间求mex那种东西,发现不太好维护信息。
但是可以从暴力开始优化。设现在已经可以表示 \([1,val]\) 内的数,那么答案 \(ans=val+1\)。
现在新加一个数 \(a_i\),要是 \(a_i>val+1\) 则 \(ans\) 不变。
要是 \(a_i\le val+1\) 则 \(ans=val+a_i+1\)。再假设区间 \([1,val]\) 是从所有值域在 \([1,x]\) 内的数拼凑出来的,那就有 \(a_i\in [x+1,val+1]\),每次可以找到 \([l,r]\) 内所有在这个区间的 \(a_i\)。则添加之后两个值域:\([1,val]->[1,val+\sum a_i],[1,x]->[1,val]\)。
找不到合适的 \(a_i\) 时相当于没法取了,把答案输出,\(a_i\) 的维护是主席树板子。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号