状压dp小结

状压 dp 就是把状态压缩为一个数方便储存和处理，特点是 \(\Theta(2^{num})\) 的时间复杂度和大量的位运算操作。极小的特定数据上限使得面对相关题目时很容易想到使用此方法，不过具体如何处理还要思考。

在此声明本文的常用新定义：

• \(S,S'...\)：我称作状压状态，表现为一个正整数，其二进制形式下的 1 与 0 表示决策。
• \(st\)：我称作合法状态数组，状压 dp 核心思想为枚举所有二进制状态，用此数组存储大部分情况下可用或能够满足基本条件的状态。
• \(check\) 集合，出现在我文中的状态转移方程中，表示为不同状压状态能够进行转移的先决条件，大多按题目而定。
• \(ln\)：我称作行条件数组，矩阵上的状压 dp 喜欢给出不可放置元素的位置，我们要用 \(ln\) 数组预先处理这些位置。

状压 dp 的矩阵态

特点是给出边界小的矩阵进行填充。

例题

题意：求出方格内不在特定位置且互不相临的填充色块方案总数。

矩阵上的状压 dp 常使用数字的二进制表示行状态。

具体地，在本题中，\((11001)_2\) 可以代表该行的第 1，2，5 位不能进行填充操作。

显然，赋初值中所规定的格子，与已填充格子上下左右相邻的格子是不可以被填充的。

先处理赋初值，使用 \(ln[i]\) 表示第 \(i\) 行的状态，同样使用状态压缩方法。

	for(int i=1;i<=n;i++){
		for(int j=1,val;j<=m;j++){
			scanf("%lld",&val);
			ln[i]=(ln[i]<<1)+val;
		}
	}

\(ln\) 数组中的数字化为二进制后，第 \(i\) 行第 \(j\) 位为 1 代表 \(map[i][j]\) 已经被规定不得填充。

竖直与水平相邻一般需要分开处理，比较巧妙的手段如下：

水平：

	toT=(1<<m)-1;
	for(int i=1;i<=toT;i++){//一般枚举所有状态，扔掉不合格状态
		if(i&(i<<1))continue;
		st[++tot]=i;
	}//水平处理，如果当前二进制数左右移一位后与原先位能够取与则状态中一定有1相邻

竖直判定在 dp 中实现。

由于我们是逐行 dp 的，所以当前状态与待转移状态不得取按位与，否则说明一定有某位重叠。

关于转移：

令 \(dp[i][j]\) 表示第 \(i\) 行状态为 \(j\) 时的可选方案数，\(dp[i][j]\) 由 \(dp[i-1][j_{1...k}]\) 转移而来。且 \(\forall j_i,j_i\in st,j_i \&j=0 ,j,j_i|ln_i=ln_i\)，即两个状态水平竖直不相邻，且两状态都不与当前行不允许放置的位置重合。

#include<bits/stdc++.h>
#define int long long
#define lowbit(p) p&(-p)
#define MAXN 15
#define N (1<<12)+5
using namespace std;
const int p=100000000;
int n,m;
int ln[MAXN];
int st[N];
int dp[MAXN][N];
int toT,tot,ans;
int vis[MAXN][N];
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		for(int j=1,val;j<=m;j++){
			scanf("%lld",&val);
			ln[i]=(ln[i]<<1)+val;
		}
	}
	toT=(1<<m)-1;
	for(int i=1;i<=toT;i++){
		if(i&(i<<1))continue;
		st[++tot]=i;
	}
	dp[0][0]=vis[0][0]=1;
	for(int loc=1;loc<=n;loc++){
		for(int i=0;i<=tot;i++){
			int s1=st[i];
			if(ln[loc]==(ln[loc]|st[i])){
				vis[loc][i]=1;
				for(int j=0;j<=tot;j++){
					int s2=st[j];
					if(!vis[loc-1][j])continue;
					if(st[i]&st[j])continue;
					dp[loc][i]=(dp[loc][i]+dp[loc-1][j])%p;
				}
			}
		}
	}
	for(int i=0;i<=tot;i++)
		ans=(ans+dp[n][i])%p;
	printf("%lld",ans%p);	
	return 0;
}

互不侵犯

题意：在 \(N*N\) 方格内放置 $ K$ 个元素，使得两个元素上下左右不相邻，求总放置方案。

注意到 \(N<=9\) 可以状压本行的状态，由于题目限制了元素的数量但有 \(K<=81\) ，所以可以直接给 dp 数组在开一个维度维护元素个数。

规定 \(dp[i][k][S]\) 为第 \(i\) 行状态为 \(S\) 时，正好放置了 \(k\) 个元素的总方案数。

\[ans=\sum_{S\in U}dp[N][K][S] \]

状态转移方程：

\[dp[i][k+cnt[i]][S]=\sum_{S'\in check}dp[i-1][k][S'] \]

对于 \(check\)，我们在保证上下左右不相邻的基础上要保证斜向不相邻。判定条件很好推： \(\forall S,S',S\&(S'<<1)=0\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k,ans;
int dp[10][101][1<<11];//第i行放j个王时状态为k的方案数 
int pre[1<<11],chk[1<<11],tmp;//状态s王数，横向不矛盾状态 
signed main(){
	scanf("%lld%lld",&n,&k);
	dp[0][0][0]=1;
	for(int s=0;s<(1<<n);s++){
		int s1=s,cnt=0;
		while(s1){
			if(s1&1)cnt++;
			s1>>=1;
		}
		pre[s]=cnt; 
		if(!((s<<1)&s)&&!((s>>1)&s))chk[++tmp]=s;
	}
	for(int i=1;i<=n;i++){
		for(int l=1;l<=tmp;l++){
			int s1=chk[l];
			for(int r=1;r<=tmp;r++){
				int s2=chk[r];
				if(!(s1&s2)&&!((s2<<1)&s1)&&!((s2>>1)&s1)){
					for(int j=0;j<=k;j++)
						if(j-pre[s1]>=0)dp[i][j][s1]+=dp[i-1][j-pre[s1]][s2];
				}
			}
		}
	}
	for(int i=1;i<=tmp;i++)ans+=dp[n][k][chk[i]];
	printf("%lld",ans);
	return 0;
}

这个码子是当初自学时对着题解抄的，所以马蜂异常。

炮兵阵地

是一道臭名昭彰的状压。

dp 问题主要分为决策个数问题和最优决策问题。这个属于后者。

题意：给定一个地图，有些区块可以放置元素，重新定义元素相邻为一个元素上下左右两格内有其他元素，求出最多可以放置最多的元素，使得任意两元素不相邻。

注意到有地图限制，所以我们使用例题的方法定义 \(ln[i]\) 的二进制表示第 \(i\) 行的可放置状态，为 1 则可放置否则不可放置。

由于相邻的重定义，影响当前 \(i\) 行状态抉择的因素将扩展至 \(i-2\) 行

规定 \(dp[i][S][S']\) 为第 \(i\) 行状态为 \(S\) 上一行决策为 \(S'\) 的最优决策。推出方程与答案：

\[dp[i][S][S']=max_{S',S''\in check}\{dp[i-1][S'][S'']\}+cnt[S] \]

\[ans=max_{S,S'\in check}\{dp[n][S][S']\} \]

先把预处理打出来：

	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		char str[MAXM];
		scanf("%s",str+1);
		for(int j=1;j<=m;j++)ln[i]=(ln[i]<<1)+(str[j]=='P'?1:0);
	}	
	int toT=(1<<m)-1;
	for(int i=1;i<=toT;i++){
		if((i&(i<<1))||(i&(i<<2)))continue;
		st[++tot]=i;
		int tmp=i;
		while(tmp){
			++cnt[tot];
			tmp-=lowbit(tmp);
		}
	}//地图行状态与左右不相邻状态处理。

考虑到往上两行都会对当前抉择产生影响，我们容易得到当前决策，上次与上上次决策 \(S,S'S''\)需满足：

\[\forall S,S'S''\in check,S\&S'=S'\&S''=S\&S''=0 \]

我们使用 \(vis_{i,S}\) 表示 \(S\) 状态满足了第 \(i\) 行的要求即 \(ln[i]|S=ln[i]\)，dp 该行时就地存储 \(vis\) 供之后的转移使用。

于是得到代码：

#include<bits/stdc++.h>
#define MAXN 105
#define MAXM 15
#define N (1<<10)+5
#define lowbit(p) p&(-p)
using namespace std;
int n,m,tot,ans;
int ln[MAXN];
int st[N],cnt[N];
int dp[MAXN][N][N];
int vis[MAXN][N];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		char str[MAXM];
		scanf("%s",str+1);
		for(int j=1;j<=m;j++)ln[i]=(ln[i]<<1)+(str[j]=='P'?1:0);
	}	
	int toT=(1<<m)-1;
	for(int i=1;i<=toT;i++){
		if((i&(i<<1))||(i&(i<<2)))continue;
		st[++tot]=i;
		int tmp=i;
		while(tmp){
			++cnt[tot];
			tmp-=lowbit(tmp);
		}
	}
	for(int i=1;i<=tot;i++){
		if((ln[1]|st[i])==ln[1]){
			vis[1][i]=1;
			dp[1][i][0]=cnt[i];
		}
	}
	for(int i=0;i<=tot;i++){
		if((ln[2]|st[i])==ln[2]){
			vis[2][i]=1;
			for(int j=0;j<=tot;j++){
				if(!vis[1][j])continue;
				int s1=st[i],s2=st[j];
				if(s1&s2)continue;
				dp[2][i][j]=max(dp[2][i][j],dp[1][j][0]+cnt[i]);
			}
		}
	}
	for(int loc=3;loc<=n;loc++){
		for(int i=0;i<=tot;i++){
			if((ln[loc]|st[i])==ln[loc]){
				vis[loc][i]=1;
				for(int j=0;j<=tot;j++){
					if(!vis[loc-1][j])continue;
					int s1=st[i],s2=st[j];
					if(s1&s2)continue;
					for(int k=0;k<=tot;k++){
						if(!vis[loc-2][k])continue;
						int s3=st[k];
						if(s3&(s1|s2))continue;
						dp[loc][i][j]=max(dp[loc][i][j],dp[loc-1][j][k]+cnt[i]);
					}
				}
			}
		}
	}
	for(int i=0;i<=tot;i++){
		for(int j=0;j<=tot;j++){
			ans=max(ans,dp[n][i][j]);
		}
	}
	printf("%d",ans);
	return 0;
}

但是我觉得这个 \(vis\) 非常的 useless，完全可以将其塞进合理状态数组 \(st\) 中，具体的，规定 \(st_{i,j}\) 为第 \(i\) 行的第 \(j\) 个可用状态。修改每行可用状态数为 \(tot_i\)，转移时直接用 \(tot_i\) 遍历第 \(i\) 行可用信息，由于状压bug主要聚集在 dp 部分，因而可以有效减小debug难度。至少我是这么觉得的。

#include<bits/stdc++.h>
#define MAXN 105
#define MAXM 15
#define N (1<<10)+5
#define lowbit(p) p&(-p)
using namespace std;
int n,m,ans;
int toT,tot[MAXN];
int ln[MAXN],st[MAXN][N],cnt[MAXN][N];
int dp[MAXN][N][N];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		char str[MAXM];
		scanf("%s",str+1);
		for(int j=1;j<=m;j++)ln[i]=(ln[i]<<1)+(str[j]=='P'?1:0);
	}
	toT=(1<<m)-1;
	for(int loc=1;loc<=n;loc++){
		for(int i=0;i<=toT;i++){
			if((i&(i<<1))||(i&(i<<2)))continue;
			if((i|ln[loc])==ln[loc]){
				st[loc][++tot[loc]]=i;
				int tmp=i;
				while(tmp){
					++cnt[loc][tot[loc]];
					tmp-=lowbit(tmp);
				}
			}
		}
	}
	for(int i=0;i<=tot[1];i++)dp[1][st[1][i]][0]=cnt[1][i],ans=max(ans,cnt[1][i]);
	for(int i=0;i<=tot[2];i++){
		int s1=st[2][i];
		for(int j=0;j<=tot[1];j++){
			int s2=st[1][j];
			if(s1&s2)continue;
			dp[2][s1][s2]=max(dp[2][s1][s2],dp[1][s2][0]+cnt[2][i]);
			ans=max(ans,dp[2][s1][s2]);
		}
	}
	for(int loc=3;loc<=n;loc++){
		for(int i=0;i<=tot[loc];i++){
			int s1=st[loc][i];
			for(int j=0;j<=tot[loc-1];j++){
				int s2=st[loc-1][j];
				if(s1&s2)continue;
				for(int k=0;k<=tot[loc-2];k++){
					int s3=st[loc-2][k];
					if((s1|s2)&s3)continue;
					dp[loc][s1][s2]=max(dp[loc][s1][s2],dp[loc-1][s2][s3]+cnt[loc][i]);
					ans=max(ans,dp[loc][s1][s2]);
				}
			}
		}
	}
	printf("%d",ans);
	return 0;
}

状态压缩 dp 的游离态

我们发现矩阵上的状压 dp 是很公式化的，状压 dp 的难度主要体现在非矩阵问题上如何想到和处理状压。

排列

题面很清晰不翻译。

注意到 \(s<=10,d<=1000\)，显然要对字符串进行状压。

很容易被"整除"这个条件误导，事实上我们可以处理整除的推广即余数，我们令 \(dp[S][k]\) 为在字符串中选择状态为 \(S\) 的元素排列得到余数为 \(k\) 的方案数。得到答案与方程：

\[ans=dp[(1<<n)-1][0] \]

\[dp[S|(1<<(j-1))][(10k+str[j])\%d]=\sum_{0<=k<d}{dp[S][k]} \]

与先前相似地，待添加的第 \(j\) 位不能存在于待转移的状态中。

于是按照上面码出来：

#include<bits/stdc++.h>
#define int long long
#define MAXN 1005
#define MAXM 15
#define N (1<<10)+5
using namespace std;
int T;
int d,tot;
int dp[N][MAXN];
bool vis[MAXM];
signed main(){
	scanf("%lld",&T);
	while(T--){
		char str[MAXM];
		scanf("%s%lld",str+1,&d);
		int len=strlen(str+1);
		tot=(1<<len)-1;
		memset(dp,0,sizeof(dp));
		dp[0][0]=1;
		for(int i=0;i<=tot;i++){
			memset(vis,0,sizeof(vis));
			for(int j=1;j<=len;j++){
				if(vis[str[j]-'0'])continue;
				if(i&(1<<(j-1)))continue;
				vis[str[j]-'0']=1;
				for(int k=0;k<d;k++)
					dp[i|(1<<(j-1))][(k*10+str[j]-'0')%d]+=dp[i][k];
			}
		}
		printf("%lld\n",dp[tot][0]);
	}
	return 0;
}

愤怒的小鸟

我觉得这道题很毒瘤，不知道为什么题解里没有批斗其毒瘤性。

题意：给定平面上的一些点 \(p_i(x_i,y_i),1<=i<=n\)，求最少可以用几条过原点的抛物线使得点全部在抛物线上。

注意到 \(n<=18\) 考虑用 \(S\) 表示当前小猪的存活状态，1 为死 0 为活。

引理：平面上任意横坐标不等的两点可以被一条过原点的抛物线连接。

设 \(f(x)=ax^2+bx\) 将要穿过 \(p_1(x_1,y_1),p_2(x_2,y_2)\)

\[\begin{cases} \large f(x_1)=ax_1^2+bx_1=y_1\\ \\ \large f(x_2)=ax_2^2+bx_2=y_2 \end{cases} \]

显然 \(a,b\) 可解。

\[\begin{cases} \large{a=\frac{y_2\frac{x_1}{x_2}-y_1}{x_1(x_2-x_1)}} \\ \\ \large{b=\frac{y_2(\frac{x_1}{x_2})^2-y_1}{x_1(\frac{x_1}{x_2}-1)}} \end{cases} \]

然后我们注意到 \(ans\neq n/2\) 的原因是：\(\exists p_i,i\neq 1,2,f(x_i)=y_i\)，也就是有小猪被一条抛物线顺带打死了。

这启示我们这样得到转移方程：我们计算 \(st_{i,j}\) 为能够打死 \(i,j\) 两只猪的这条抛物线实际顺带着打死的所有猪的状态，令 \(dp[S]\) 为小猪伤亡情况为 \(S\) 时的最小代价，就当前状态考虑再打死一直活着的小猪和能它被一条抛物线打死的小猪，由此推出答案与方程：

\[ans=dp[(1<<n)-1] \]

\[dp[S|st_{i,j}]=min_{S\in check}\{dp[S]\}+1 \]

特别地，当剩余小猪集合 \(R\) 因为一些原因不足以使我们一炮打掉两个时：

\[dp[S|(1<<(j-1))]=min_{S\in check}\{dp[S]\}+1,j\in R \]

于是我们将程序分为两个部分：

• \(calc(i,j)\) 函数，负责在枚举 \(i,j\) 时获得 \(st_{i,j}\)
• 状压 dp，负责按照上文方式得到答案。

我们注意到小数精度问题，这里使用一个科技：

fabs()

求出当前数在实数意义下的绝对值。

#include<bits/stdc++.h>
#define MAXN 20
#define N (1<<18)+5
using namespace std;
int T,n,_;
struct node{
	double x,y;
}p[MAXN];
int dp[N];
int st[MAXN][MAXN];
int lk[N];
inline int calc(int p1,int p2){
	double x1=p[p1].x,y1=p[p1].y;
	double x2=p[p2].x,y2=p[p2].y;
	if(fabs(x1-x2)<1e-7)return 0;
	double a=1.0*(x1/x2*y2-y1)/(x1*x2-x1*x1);
	double b=1.0*(y2*(x1*x1)/(x2*x2)-y1)/(x1*x1/x2-x1);//计算二次函数
	int res=0;
	if(fabs(a)<1e-7)return 0;
	if(a>=0)return 0;//a应该小于0
    //实际会出现a为极大负数的情况，这时得用fabs特判
    //幽默的是不加这句过不了样例却能A，那么多数据都卡不到这种特解，建议把样例搬进数据。
	for(int i=1;i<=n;i++){
		int s=1<<(i-1);
		double x=p[i].x,y=p[i].y;
		if(fabs(a*x*x+b*x-y)<1e-7){//发现这只猪顺带能被打掉
			res|=s;
			dp[res]=dp[s]=1;//这只猪与目前的状态都可以被一只鸟打掉。
		}
	}
	return res;
}
int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%d%d",&n,&_);
		for(int i=1;i<=n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
		memset(dp,127,sizeof(dp));
		memset(st,0,sizeof(st));
		dp[0]=0;//初始化
		for(int i=1;i<=n;i++){
			int loc=1<<(i-1);
			dp[loc]=1;//单独打一只猪最少要1只鸟
		}
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				st[i][j]=calc(i,j);//获得能顺带被打掉的状态。
		int tot=(1<<n)-1;
		for(int i=0;i<=tot;i++){
			for(int j=1;j<=n;j++){
				int s1=1<<(j-1);
				if(i&s1==i)continue;//找到一只准备打掉的剩余猪
				for(int k=1;k<=n;k++){//枚举它能一并打掉的那个partner
					if(j==k)continue;//不能是自己
					int s2=1<<(k-1)
					if(i&s2==1)continue;//这只猪也得存活。
					dp[i|st[j][k]]=min(dp[i|st[j][k]],dp[i]+1);
				}
				dp[i|s1]=min(dp[i|s1],dp[i]+1);//如果凑不齐一对，直接用一炮换这一只猪。
			}
		}		
		printf("%d\n",dp[(1<<n)-1]);
	}	
	return 0;
}

动物园

懒得翻译。

如果它不给我状压标签我是不知道怎么切入的。

发现给出的变量都很大。然而"每个小朋友站在大围栏圈的外面，可以看到连续的 5 个围栏。" 5 这个数比较小，那么考虑枚举小孩看五个栅栏的状态。

这种方法似乎可做。栅栏中的动物是固定的，我们不妨处理出这个小孩喜欢和害怕的动物状态 \(S_l,S_f\),对于从 \(E\) 开始的一个动物选取状态 \(S\)，我们称这个状态能让小孩满意，当且仅当 \(S_l\&S!=0\) 或 \(S_f\&(\sim S)!=0\)。

注意到栅栏和小孩的位置不是一个东西，令 \(st_{i,S}\) 表示第 \(i\) 个栅栏开始状态为 \(S\) 能让小孩满意的个数，在输入时进行处理，事实上 \(st_{i,S}\in \{0,1\}\)，想想即可。

现在考虑怎么转移，如果按栅栏处理的话可以实现转移。具体地，在区间 \(E\sim E+4\) 进行操作后，同样会影响 \(E+1\sim E+5\) 的其中四位

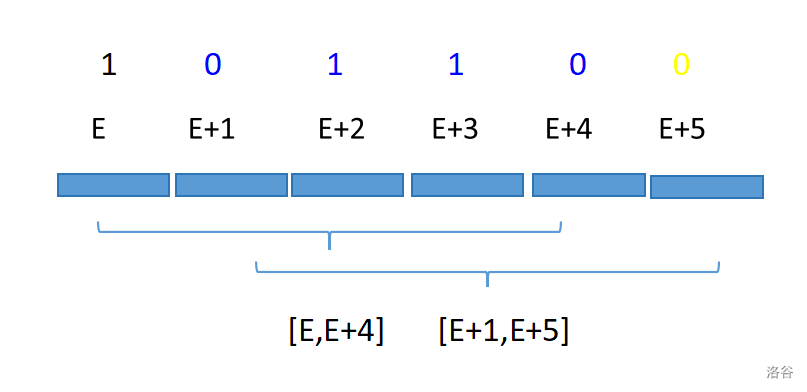
图中有 \(S=(01100)_2,S'=(10110)_2\)，我们得到两种状态的转移方式为 \(S=(S'\&15)<<1\) 或 \(S=(S'\&15)<<1|1\)，具体的选择要看 \(S\) 末尾是不是 1。

对于这样一次新的转移，我们发现 \(st_{E+1.S}\) 可能对答案做出贡献。

因此我们令 \(dp[i][S]\) 为第 \(i\) 个栅栏开始延后五位状态为 \(S\) 的最优解。 得到答案与状态转移方程:

\[ans=max_{S\in U}\{dp[n][S]\} \]

\[dp[i][S]=max_{S\in check}\{dp[i-1][S']+st[i][S]\} \]

#include<bits/stdc++.h>
#define MAXN 50005
#define N (1<<5)+5
using namespace std;
int n,c,tot=31;
int st[MAXN][N];
int dp[MAXN][N],ans;
int main(){
	scanf("%d%d",&n,&c);
	for(int i=1,e,f,l;i<=c;i++){
		scanf("%d%d%d",&e,&f,&l);
		int sl=0,sf=0;
		for(int j=1,val;j<=f;j++){
			scanf("%d",&val);
			val=(val-e+n)%n;
			sf|=(1<<val);
		}
		for(int j=1,val;j<=l;j++){
			scanf("%d",&val);
			val=(val-e+n)%n;
			sl|=(1<<val);
		}
		for(int j=0;j<=tot;j++)if((j&sl)||(~j&sf))++st[e][j];
	}
	for(int s=0;s<=tot;s++){
		memset(dp[0],128,sizeof(dp[0]));
		dp[0][s]=0;
		for(int i=1;i<=n;i++){
			for(int j=0;j<=tot;j++){
				dp[i][j]=max(dp[i-1][(j&15)<<1],dp[i-1][(j&15)<<1|1])+st[i][j];
			}
		}
		ans=max(ans,dp[n][s]);
	}
	printf("%d",ans);
	return 0;
}

集合选数

这个题有科技。

题意:求出 \(N\) 所有满足条件 \(F\) 的子集 \(N_S\)，规定 \(F(N_S):\forall x_i\in N_S,2x_i\notin N_S,3x_i\notin N_S\)。

发现不会写，题解说：构造一个矩阵

\[\begin{bmatrix} 2^03^0x&\cdots&2^03^{k_1}x\\ 2^13^0x&\cdots&2^13^{k_2}x\\ \vdots&\ddots&\vdots\\ 2^{k_2}3^0x&\cdots&2^{k_2}3^{k_1}x \end{bmatrix} \]

横向为公比为 \(3\) 的等比数列，纵向公比为 \(2\)。

于是条件 \(F\) 等价于：在矩阵中选取任意个元素满足各元素不相邻。

但发现 \(n=6\) 时:

\[\begin{bmatrix} 1&3\\ 2&6\\ 4&12 \end{bmatrix} \]

元素 \(12\) 冗余了，元素 \(5\) 缺失了，似乎不可做。

题解说：矩阵不必是完全的，矩阵不必只有一个。

注意到 \(5\) 无法被覆盖的同时，\(10,15,30\dots\) 同样不可被覆盖，这些不可被覆盖的元素又可以成为新矩阵，在不能覆盖的元素可以再构造矩阵，一直构造下去即可完全填充（感觉好玄学）。

这里回到炮兵阵地的改版代码。

	for(int loc=1;loc<=n;loc++){
		for(int i=0;i<=toT;i++){
			if((i&(i<<1))||(i&(i<<2)))continue;
			if((i|ln[loc])==ln[loc]){
				st[loc][++tot[loc]]=i;
				int tmp=i;
				while(tmp){
					++cnt[loc][tot[loc]];
					tmp-=lowbit(tmp);
				}
			}
		}
	}

\(tot\) 数组的引入已经启示我们不完全矩阵的处理方法。

统计矩阵每行的实际长度计算 \(tot_i\) 即可。最后不同矩阵的方案要相乘，因为乘法原理。

#include<bits/stdc++.h>
#define N (1<<11)+5
#define MAXN 20
#define MAXM 100005
#define int long long
using namespace std;
const int p=1e9+1;
int T,n,m[MAXN];
bool vis[MAXM];
int st[N],dp[MAXN][N];
int tot[MAXN];
int ans=1;
inline void build(int rt){
	n=1;
	memset(m,0,sizeof(m));
	memset(dp,0,sizeof(dp));
	for(int i=rt;i<=T;i*=2,n++){
		for(int j=i;j<=T;j*=3)++m[n],vis[j]=1;
	}
	n--;
	for(int i=1;i<=n;i++)tot[i]=(1<<m[i])-1;
	for(int i=0;i<=tot[1];i++)dp[1][i]=st[i];
	for(int loc=2;loc<=n;loc++){
		for(int i=0;i<=tot[loc];i++){
			if(!st[i])continue;
			for(int j=0;j<=tot[loc-1];j++){
				if(!st[j])continue;
				if(i&j)continue;
				dp[loc][i]=(dp[loc][i]+dp[loc-1][j])%p;
			}
		}
	}
	int val=0;
	for(int i=0;i<=tot[n];i++)val=(val+dp[n][i])%p;
	ans=ans*val%p;
}
signed main(){
	for(int i=0;i<=(1<<11)-1;i++){
		if(i&(i<<1))continue;
		st[i]=1; 
	}
	scanf("%lld",&T);
	for(int i=1;i<=T;i++){
		if(!vis[i])build(i);
	}	
	printf("%lld",ans);
	return 0;
}

说起来很简单，做题时不看题解很难想到，实现细节也多。

总结：比树剖，鞋油难