整理:平衡树
关于平衡树的整理
1.前置知识:二叉搜索树
二叉搜索树(Binary Search Tree),简称 BST,是一类带权二叉树,这类二叉树满足:左子树中的所有节点的权值都小于根节点,而右子树中的所有节点的权值都大于根节点。
一般在实现二叉搜索树的时候,我们会将权值相同的节点并成一个节点,而不是视为多个节点,可以避免讨论一个相同权值的节点应该放在左子树还是右子树。
二叉搜索树有三条个人认为比较重要的性质:
- 二叉搜索树的中序遍历是一个递增序列。
- 二叉搜索树的最优高度为 \(\log n\),最劣高度为 \(n\)
- 对于一个相同的元素集合,可以构造出多种不同的二叉平衡树。
根据二叉搜索树的定义,可以很简单地进行如下操作:
- 查找最小/大值。
- 搜索一个指定元素。
- 求一个元素在序列中的排名。
- 查找指定排名的元素。
- 求一个元素的前驱(小于它的最大值)
- 求一个元素的后继(大于它的最小值)
- 在二叉搜索树中插入一个元素。
- 在二叉搜索树中删除一个元素。
下面来描述如何实现二叉搜索树的这几项操作。
(注:此部分所有代码未经实战,请谨慎使用)
0.二叉搜索树的定义
这里给出我下文使用的二叉搜索树的相关变量定义和一些基础函数。
struct Binary_Search_Tree{
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num;
int val[N],cnt[N],siz[N],fa[N],ch[N][2];
/*
val[p] 表示 p 节点的权值
cnt[p] 表示当前权值等于 val[p] 的元素有多少个
siz[p] 表示以 p 节点为根的子树中的节点个数,这里包含被合并的节点
fa[p] 表示 p 节点的父亲
ch[p][0/1] 表示 p 的左/右儿子
*/
int New(int v){//给 v 这个权值新建一个节点
++num;
cnt[num]=siz[num]=1;
val[num]=v;
fa[num]=ch[num][0]=ch[num][1]=0;
return num;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
#undef Siz
}
注意:在阅读下列操作的实现时,请牢记:BST 所满足的性质,也就是一个节点的左子树的所有元素都小于这个节点的权值,右子树的所有元素都大于这个节点的权值,当你无法理解为什么这样做的时候,默念一遍这个性质,然后再思考。
注:下列操作中,部分操作的依据十分相似,可能会出现只是部分关键词不同的情况,请注意分辨!
1.查找最小/大值
我们之前说过二叉搜索树的中序遍历是一个递增序列,所以当前的最小值就是二叉搜索树的左链顶端,当前最大值就是二叉搜索树的右链顶点。
int getMin(int p){
while(ch[p][0])p=ch[p][0];
return val[p];
}
int getMax(int p){
while(ch[p][1])p=ch[p][1];
return val[p];
}
2.搜索一个指定元素
由于二叉搜索树的性质,搜索一个指定元素 \(v\),考虑当前节点为 \(p\),然后分类讨论。
- 如果 \(p\) 为空,那么就表示找不到。
- 如果 \(val_p\) 和 \(v\) 相等,那么就表示找到了。
- 如果 \(val_p\) 大于 \(v\),那么如果 \(v\) 存在,那么就在 \(p\) 的左子树中,递归查找即可。
- 如果 \(val_p\) 小于 \(v\),那么如果 \(v\) 存在,那么就在 \(p\) 的右子树中,递归查找即可。
bool search(int p,int v){
if(!p)return false;
if(val[p]==v)return true;
if(val[p]>v)return search(ch[p][0],v);
return search(ch[p][1],v);
}
3.求一个元素在序列中的排名
这里的排名定义为序列中严格小于这个值的元素个数加一,所以我们求出序列中严格小于这个值的元素个数即可。假设现在递归到节点 \(p\),分类讨论。
- \(val_p\) 等于 \(v\),那么返回 \(siz_{ch_{p,0}}\),因为左子树中的所有节点都小于 \(v\)。
- \(val_p\) 大于 \(v\),那么向左子树中递归,因为这个节点和右子树中的节点权值一定大于 \(v\)。
- \(val_p\) 小于 \(v\),那么先向右子树中递归,然后将结果加上 \(siz_{ch_{p,0}}+cnt_p\),因为左子树和这个节点的权值一定小于 \(v\)。
int getrank(int p,int v){
if(val[p]==v)return Siz(ch[p][0]);
if(val[p]>v)return getrank(ch[p][0],v);
return getrank(ch[p][1],v)+Siz(ch[p][0])+cnt[p];
}
4.查找指定排名的元素
同样分类讨论,假定现在递归到节点 \(p\),要求求出排名为 \(rank\) 的值。
- \(rank\le siz_{ch_{p,0}}\),那么向左子树中递归,因为左子树中的元素排名为 \(1\sim siz_{ch_{p,0}}\)。
- \(siz_{ch_{p,0}}<rank\le siz_{ch_{p,0}}+cnt_p\),那么返回 \(val_p\),因为这个节点的元素排名为 \(siz_{ch_{p,0}}+1\sim siz_{ch_{P,0}}+cnt_p\)。
- \(siz_{ch_{p,0}}+cnt_p<rank\),那么向右子树中递归,查找排名为 \(rank-siz_{ch_{p,0}}-cnt_p\) 的元素,因为右子树中的元素排名为 \(siz_{ch_{p,0}}+cnt_p+1\sim siz_p\)。
int getnum(int p,int rank){
if(rank<=Siz(ch[p][0]))return getnum(ch[p][0],rank);
if(rank<=Siz(ch[p][0])+cnt[p])return val[p];
return getnum(ch[p][1],rank-Siz(ch[p][0])-cnt[p]);
}
5.求一个元素的前驱(小于它的最大值)
假设当前递归到节点 \(p\),要求求 \(v\) 的前驱,分类讨论。
- \(val_p\) 大于等于 \(v\),那么右子树中的元素都大于 \(v\),直接向左子树中递归即可。
- \(val_p\) 小于 \(v\),那么先用 \(val_p\) 更新答案,然后向右子树中递归,因为左子树中的元素虽然都满足条件,但是值都小于 \(val_p\)。
void findpre(int p,int v,int& ans){
if(!p)return ;
if(val[p]>=v)find_pre(ch[p][0],v,ans);
else{
tomax(ans,val[p]);
find_pre(ch[p][1],v,ans);
}
}
6.求一个元素的后继(大于它的最小值)
与求前驱类似,假设当前递归到节点 \(p\),要求求 \(v\) 的后继,分类讨论。
- \(val_p\) 小于等于 \(v\),那么左子树中的元素都小于 \(v\),直接向右子树中递归即可。
- \(val_p\) 大于 \(v\),那么先用 \(val_p\) 更新答案,然后向左子树中递归,因为右子树中的元素虽然都满足条件,但是值都大于 \(val_p\)。
void findsuf(int p,int v,int& ans){
if(!p)return ;
if(val[p]<=v)find_suf(ch[p][1],v,ans);
else{
tomin(ans,val[p]);
find_suf(ch[p][0],v,ans);
}
}
7.插入一个元素
考虑向树中插入一个权值为 \(v\) 的节点,当前递归到一个节点 \(p\),然后分类讨论。
- 如果 \(p\) 为空,那么就新建一个节点。
- 如果 \(val_p\) 等于 \(v\),那么就将 \(cnt_p\) 加一。
- 如果 \(val_p\) 大于 \(v\),那么就递归向左子树中插入。
- 如果 \(val_p\) 小于 \(v\),那么就递归向右子树中插入。
void insert(int &p,int v){
if(!p){
p=New(v);
return ;
}
if(val[p]==p)cnt[p]++;
else if(val[p]>v)insert(ch[p][0],v);
else insert(ch[p][1],v);
return ;
}
8.删除一个元素
考虑在树中删除一个权值为 \(v\) 的元素,当前递归到一个节点 \(p\),不妨假定 \(v\) 在树中一定存在。
- \(val_p\) 等于 \(v\),那么就将 \(cnt_p\) 减一,然后继续分类讨论。
- \(cnt_p\) 仍然大于 \(0\),那么直接返回。
- \(cnt_p\) 等于 \(0\),需要删除这个节点,首先如果这个节点是个叶子节点直接删掉,然后如果这个节点只有一个儿子,那么直接将这个儿子接到这个节点的父亲上,否则我们需要找一个节点代替它的位置,考虑右子树的左链顶点,这个节点的权值大于左子树中的所有节点,又是右子树中最小的节点,所以恰好可以放在 \(p\) 这个位置,成为新的根,当然选择左子树的右链顶点也是可以的。
- \(val_p\) 大于 \(v\) ,向左子树中递归。
- \(val_p\) 小于 \(v\) ,向右子树中递归。
void delet(int &p,int v){
if(!p)return ;
if(val[p]==v){
cnt[p]--;
if(cnt[p]==0){
int now=ch[p][0];
while(ch[now][1])now=ch[now][1];
p=now;
}
}else if(val[p]>v)delet(ch[p][0],v);
else delet(ch[p][1],v);
pushup(p);
}
2.使用平衡树的必要和平衡树的定义
显然所有与二叉平衡树相关的操作时间复杂度都是 \(O(h)\),也就是与树高相关,但是前面说过:
二叉搜索树的最优高度为 \(\log n\),最劣高度为 \(n\)
也就是说直接使用二叉搜索树极可能会导致 TLE 的结果,并且十分好卡(只需要一个递增或递减序列就可以将 BST 卡成一条链),所以我们需要一些新的数据结构。
所以我们对二叉搜索树定义一个性质:平衡性,同时将拥有平衡性的二叉搜索树称为平衡树。
不同的平衡树可能对平衡的定义不同,但都是为了限定树高以保证正确的时间复杂度,一般为对数时间复杂度。
一般的,我们认为二叉搜索树的左右子树深度之差不超过 \(1\) 时,那么称这棵二叉搜索树平衡。
平衡树正是这样一种数据结构,它的节点权值满足了 BST 的性质,同时又经过一些操作保证自己的平衡性,限定树高然后保证相关操作的时间复杂度正确。
3.请保持平衡
玩重返未来玩的
上面说过,平衡树需要通过一些操作保证平衡性,而这种操作最常见的就是旋转节点(rotate),也就是两种旋转,称为右旋和左旋。
由于左旋和右旋互为逆过程,我们这里着重讲述右旋的过程,左旋过程可以类比。
1.右旋(zig/right rotate)
对于一个节点,将左儿子向右旋转到当前这个节点的位置,并且保证二叉搜索树的性质。
我们假定现在的根为 \(p\),根的左儿子为 \(ls\),左儿子的右儿子为 \(lrs\),那么根据二叉搜索树的性质可以得到,以 \(ls\) 为根的这棵子树中,所有节点的权值都比 \(p\) 小。
首先我们不妨先在脑海里将整棵树分成四份:以 \(ls\) 为根的子树,以 \(lrs\) 为根的子树,以 \(p\) 为根的子树和切割剩下来的一部分,如图所示。
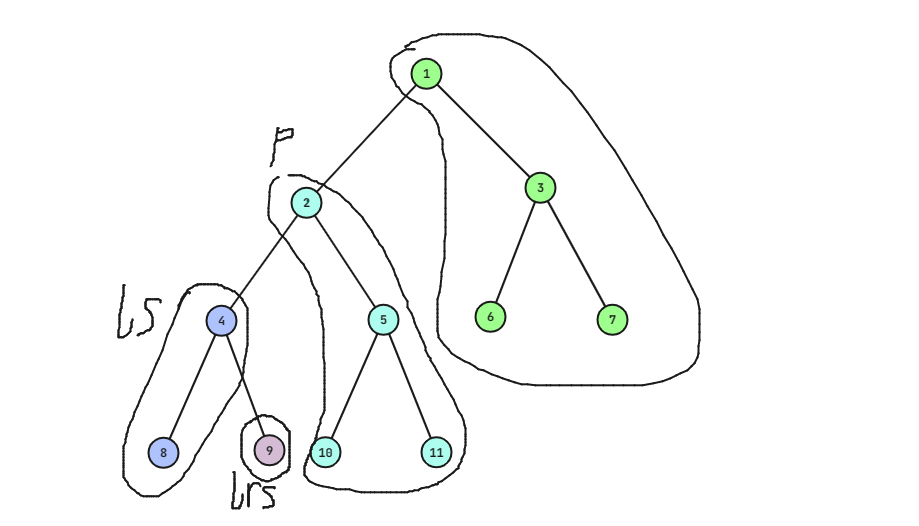
根据二叉平衡树的性质,我们可以得到如下信息:按照权值从大到小排序,分别为 \(p\) 这部分子树,\(lrs\) 这部分子树和 \(ls\) 这部分子树。
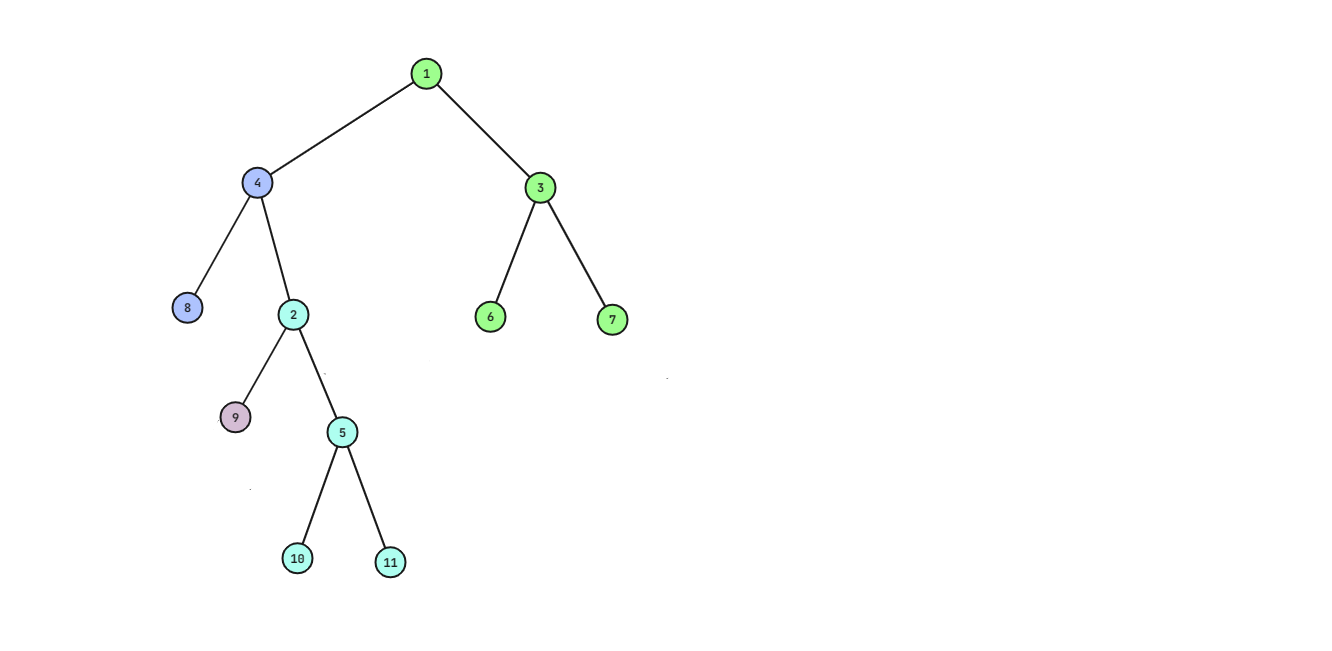
由于现在我们需要 \(ls\) 代替 \(p\) 的位置,所以 \(ls\) 的右儿子从 \(lrs\) 变成 \(p\),而 \(lrs\) 应当变成 \(p\) 的左儿子,因为 \(lrs\) 的权值大于 \(ls\),应该放在 \(ls\) 的右子树中,又因为 \(lrs\) 的权值小于 \(p\),所以应该放在 \(p\) 的左子树,又因为 \(p\) 的左子树正好被我们切下来了,所以可以直接接上,也就是说,整棵树变成下图的样子(点的编号和原图编号对应)。
2.左旋(zag/left rotate)
对于一个节点,将右儿子向左旋转到当前这个节点的位置,并且保证二叉搜索树的性质。
和上面过程同理,只是左右互换而已,也就是右旋之后的树经过一次左旋就可以变回去。
如果不理解的话,将右旋的过程中,将所有的右改成左,将所有的左改成右,就是左旋的过程了。
4.Treap(树堆)
Treap 就是一种平衡树,它通过另一种数据结构的性质来保证平衡性:堆。
其实从 Treap 的名字就可以发现端倪:Treap 就是 tree 和 heap 的合成词
我们给平衡树中的节点附加一个随机权值 \(c\),要求节点原有的权值满足 BST 的性质,而 \(c\) 满足堆的性质(大根堆和小根堆均可)。
关于树堆时间复杂度的具体证明可以看 OI Wiki(因为我不会证明)。
这里我们先给 Treap 的第一种实现形式:有旋 Treap 。
5.有旋 Treap
有旋 Treap,即使用上面的旋转操作来保证平衡性并使得 \(c\) 满足我们要求的堆的性质。
由于平衡树是一种二叉搜索树,所以仍然可以类似二叉搜索树做出如下操作:
- 查找最小/大值。
- 搜索一个指定元素。
- 求一个元素在序列中的排名。
- 查找指定排名的元素。
- 求一个元素的前驱(小于它的最大值)
- 求一个元素的后继(大于它的最小值)
- 在二叉搜索树中插入一个元素。
- 在二叉搜索树中删除一个元素。
(注:此部分所有代码都经过实战检验,可以放心使用)
0.有旋 Treap的定义
同样给出我下文使用的有旋 Treap 的相关变量定义和一些基础函数。
struct Treap{
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num;
int val[N],cnt[N],siz[N],ch[N][2];
unsigned int c[N];
mt19937 ran(time(0));
/*
val[p] 表示 p 节点的权值(满足 BST 性质的权值)
c[p] 表示 p 节点的随机权值(满足堆性质的权值)
cnt[p] 表示当前权值等于 val[p] 的元素有多少个
siz[p] 表示以 p 节点为根的子树中的节点个数,这里包含被合并的节点
fa[p] 表示 p 节点的父亲
ch[p][0/1] 表示 p 的左/右儿子
*/
void New(int &p,int v){
p=++num;
val[num]=v,c[p]=ran();
cnt[p]=siz[p]=1;
fa[p]=ch[p][0]=ch[p][1]=0;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
void rotate(int &p,bool opt){
//opt = 0 表示右旋,opt =1 表示左旋
int x=ch[p][opt];
ch[p][opt]=ch[x][opt^1];
ch[x][opt^1]=p;
pushup(ch[p][opt]),pushup(ch[x][opt^1]);
p=x;
}
#undef Siz
}
1~6.操作与BST相同的部分
如标题,这一部分的代码实现其实与 BST 是一模一样的,可以直接照抄,这里不再过多解释,忘记的可以翻回去看看。
将代码整合后粘贴如下:
int getMin(int p){
while(ch[p][0])p=ch[p][0];
return val[p];
}
int getMax(int p){
while(ch[p][1])p=ch[p][1];
return val[p];
}
bool search(int p,int v){
if(!p)return false;
if(val[p]==v)return true;
if(val[p]>v)return search(ch[p][0],v);
return search(ch[p][1],v);
}
int getrank(int p,int v){
if(val[p]==v)return Siz(ch[p][0]);
if(val[p]>v)return getrank(ch[p][0],v);
return getrank(ch[p][1],v)+Siz(ch[p][0])+cnt[p];
}
int getnum(int p,int rank){
if(rank<=Siz(ch[p][0]))return getnum(ch[p][0],rank);
if(rank<=Siz(ch[p][0])+cnt[p])return val[p];
return getnum(ch[p][1],rank-Siz(ch[p][0])-cnt[p]);
}
void findpre(int p,int v,int& ans){
if(!p)return ;
if(val[p]>=v)find_pre(ch[p][0],v,ans);
else{
tomax(ans,val[p]);
find_pre(ch[p][1],v,ans);
}
}
void findsuf(int p,int v,int& ans){
if(!p)return ;
if(val[p]<=v)find_suf(ch[p][1],v,ans);
else{
tomin(ans,val[p]);
find_suf(ch[p][0],v,ans);
}
}
7.加入一个节点
或许在加入一个节点的时候同时维护 BST 的性质和堆的性质十分困难,我们不妨将问题拆分开,首先根据二叉搜索树的性质将这个节点下放到叶子的位置,然后类比维护堆的操作上浮这个节点即可,注意一下如果上浮的这个节点是父节点的左儿子,那么应当右旋,反之,则应当左旋。
void insert(int &p,int v){
if(!p)return New(p,v);
if(val[p]==v)cnt[p]++;
else if(v>val[p]){
insert(ch[p][1],v);
if(c[p]>c[ch[p][1]])ratote(p,1);
}else{
insert(ch[p][0],v);
if(c[p]>c[ch[p][0]])ratote(p,0);
}
pushup(p);
}
8.删除一个节点
和 BST 的删除过程一样,我们依次递归下去,找到需要删除的节点 \(p\),然后对 \(p\) 进行修改。
首先先将 \(cnt_p\) 减一,如果减一后 \(cnt_p\) 仍然大于 \(0\),那么直接结束就可以了。
否则我们需要删除这个节点,重复如下过程:选择左右儿子中附加权值小的(如果你维护的堆是大根堆,那么选择附加权值大的),然后将这个儿子旋转上来,直到这个节点没有儿子或者只有一个儿子,然后删掉这个节点即可。
void delet(int &p,int v){
if(!p)return ;
if(val[p]==v){
cnt[p]--;
siz[p]--;
if(cnt[p])return ;
if(ch[p][0]==0&&ch[p][1]==0)return void(p=0);
if(ch[p][0]==0){
p=ch[p][1];
pushup(p);
return ;
}
if(ch[p][1]==0){
p=ch[p][0];
pushup(p);
return ;
}
int tmp=p;
if(c[ch[p][0]]<c[ch[p][1]])ratote(p,0);
else ratote(p,1);
pushup(p);
int now=tmp,pre=p;
while(ch[now][0]&&ch[now][1]){
if(c[ch[now][0]]<c[ch[now][1]])ratote(now,0);
else ratote(now,1);
pushup(now);
if(val[ch[pre][0]]==v)ch[pre][0]=now;
else ch[pre][1]=now;
pre=now;
now=tmp;
}
if(val[ch[pre][0]]==v)ch[pre][0]=ch[now][0]|ch[now][1];
else ch[pre][1]=ch[now][0]|ch[now][1];
pushup(pre);
}else if(v>val[p]){
delet(ch[p][1],v);
pushup(p);
}else{
delet(ch[p][0],v);
pushup(p);
}
}
9.完整代码
一些调试平衡树的小建议:建议在调试的时候将随机数发生器的种子固定,这样不会出现在一些种子下可以通过而在另一些种子下无法通过的情况;如果平衡树可以通过数据规模较小的测试点,但是在数据规模更大的测试点 TLE,那么检查是否为每一个节点附加了随机权值。
struct Treap{
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num;
int val[N],cnt[N],siz[N],ch[N][2];
unsigned int c[N];
mt19937 ran(time(0));
void New(int &p,int v){
p=++num;
val[num]=v,c[p]=ran();
cnt[p]=siz[p]=1;
fa[p]=ch[p][0]=ch[p][1]=0;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
void rotate(int &p,bool opt){
//opt = 0 表示右旋,opt = 1 表示左旋
int x=ch[p][opt];
ch[p][opt]=ch[x][opt^1];
ch[x][opt^1]=p;
pushup(ch[p][opt]),pushup(ch[x][opt^1]);
p=x;
}
void insert(int &p,int v){
if(!p)return New(p,v);
if(val[p]==v)cnt[p]++;
else if(v>val[p]){
insert(ch[p][1],v);
if(c[p]>c[ch[p][1]])ratote(p,1);
}else{
insert(ch[p][0],v);
if(c[p]>c[ch[p][0]])ratote(p,0);
}
pushup(p);
}
void delet(int &p,int v){
if(!p)return ;
if(val[p]==v){
cnt[p]--;
siz[p]--;
if(cnt[p])return ;
if(ch[p][0]==0&&ch[p][1]==0)return void(p=0);
if(ch[p][0]==0){
p=ch[p][1];
pushup(p);
return ;
}
if(ch[p][1]==0){
p=ch[p][0];
pushup(p);
return ;
}
int tmp=p;
if(c[ch[p][0]]<c[ch[p][1]])ratote(p,0);
else ratote(p,1);
pushup(p);
int now=tmp,pre=p;
while(ch[now][0]&&ch[now][1]){
if(c[ch[now][0]]<c[ch[now][1]])ratote(now,0);
else ratote(now,1);
pushup(now);
if(val[ch[pre][0]]==v)ch[pre][0]=now;
else ch[pre][1]=now;
pre=now;
now=tmp;
}
if(val[ch[pre][0]]==v)ch[pre][0]=ch[now][0]|ch[now][1];
else ch[pre][1]=ch[now][0]|ch[now][1];
pushup(pre);
}else if(v>val[p]){
delet(ch[p][1],v);
pushup(p);
}else{
delet(ch[p][0],v);
pushup(p);
}
}
int getMin(int p){
while(ch[p][0])p=ch[p][0];
return val[p];
}
int getMax(int p){
while(ch[p][1])p=ch[p][1];
return val[p];
}
bool search(int p,int v){
if(!p)return false;
if(val[p]==v)return true;
if(val[p]>v)return search(ch[p][0],v);
return search(ch[p][1],v);
}
int getrank(int p,int v){
if(val[p]==v)return Siz(ch[p][0]);
if(val[p]>v)return getrank(ch[p][0],v);
return getrank(ch[p][1],v)+Siz(ch[p][0])+cnt[p];
}
int getnum(int p,int rank){
if(rank<=Siz(ch[p][0]))return getnum(ch[p][0],rank);
if(rank<=Siz(ch[p][0])+cnt[p])return val[p];
return getnum(ch[p][1],rank-Siz(ch[p][0])-cnt[p]);
}
void findpre(int p,int v,int& ans){
if(!p)return ;
if(val[p]>=v)find_pre(ch[p][0],v,ans);
else{
tomax(ans,val[p]);
find_pre(ch[p][1],v,ans);
}
}
void findsuf(int p,int v,int& ans){
if(!p)return ;
if(val[p]<=v)find_suf(ch[p][1],v,ans);
else{
tomin(ans,val[p]);
find_suf(ch[p][0],v,ans);
}
}
#undef Siz
}treap;
6.有旋 Treap 和其他数据结构的对比
| 单次时间复杂度 | 常数 | 空间复杂度 | 码量 | 适用范围 | |
|---|---|---|---|---|---|
| 有旋 Treap | \(O(\log n)\) | 小 | \(O(n)\)(显然只有一倍) | 大 | 大 |
| 权值线段树(非动态开点) | \(O(\log n)\) | 大 | \(O(n)\)(当然开四倍) | 小 | 小 |
这里解释一下为什么有旋 Treap 的适用范围比权值线段树大:当权值的值域很大的时候,使用权值线段树需要离散化,但是有些时候问题强制在线,无法得到完整的序列,这个时候就不能直接使用权值线段树了(当然可以动态开点,如果你喜欢),而使用有旋 Treap 则没有这种烦恼。
7.无旋 Treap
我们发现有旋 Treap 的码量着实十分大,那么有没有一种平衡树码量小一些呢?当然是有的,就是无旋 Treap。
顾名思义,无旋 Treap 就是不用旋转操作维护平衡性的 Treap,它通过另外一种操作维护平衡性:分裂(split)和合并(merge),因此,无旋 Treap 有一个别称,称为分裂-合并 Treap。
我们接下来解释分裂和合并的具体做法。
0.无旋 Trep 的定义
同样给出我下文使用的无旋 Treap 的相关变量定义和一些基础函数。
struct Treap{
#define pii pair<int,int>
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num,rt;
int val[N],cnt[N],siz[N],ch[N][2];
unsigned int c[N];
mt19937 ran(time(0));
/*
rt 表示当前的根
val[p] 表示 p 节点的权值(满足 BST 性质的权值)
c[p] 表示 p 节点的随机权值(满足堆性质的权值)
cnt[p] 表示当前权值等于 val[p] 的元素有多少个
siz[p] 表示以 p 节点为根的子树中的节点个数,这里包含被合并的节点
fa[p] 表示 p 节点的父亲
ch[p][0/1] 表示 p 的左/右儿子
*/
void New(int &p,int v){
p=++num;
val[num]=v,c[p]=ran();
cnt[p]=siz[p]=1;
fa[p]=ch[p][0]=ch[p][1]=0;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
#undef pii
#undef Siz
}
1.分裂
分裂一般使用递归实现,返回一个二元组,分别表示将这棵子树分裂之后第一棵平衡树和第二棵平衡树的根。
分裂分为两种,一种是按排名分裂,另外一种是按值分裂,在一般的无旋 Treap 中,一般都采用后者,所以先来讲解后者的做法。
所谓按值分裂,就是将一棵平衡树按照一个权值分成两棵,并且使第一棵平衡树的权值都不大于规定的权值,第二棵平衡树的权值都大于规定的权值。
假定现在我们递归分裂到了节点 \(p\),按值分裂的权值为 \(v\),然后分类讨论。
- 如果 \(val_p\le v\),那么说明这个节点和这个节点的左子树都属于第一棵平衡树,先向右子树递归分裂,得到二元组 \((first,second)\),然后将这个节点的右儿子设置为 \(first\),然后返回 \((p,second)\)。
- 如果 \(val_p> v\),那么说明这个节点和这个节点的右子树都属于第二棵平衡树,先向左子树递归分裂,得到二元组 \((first,second)\),然后将这个节点的左儿子设置为 \(second\),然后返回 \((first,p)\)。
pii split(int p,int v){
if(!p)return {0,0};//递归边界
if(val[p]<=v){
pii tmp=split(ch[p][1],v);
ch[p][1]=tmp.first;
pushup(p);
return {p,tmp.second};
}else{
pii tmp=split(ch[p][0],v);
ch[p][0]=tmp.second;
pushup(p);
return {tmp.first,p};
}
}
而按排名分裂则略有不同,它并非按照一个权值进行分裂,而是按照树的大小进行分裂,使得第一棵平衡树的大小为规定的大小,第二棵平衡树就是剩下的部分。
假定现在我们递归分裂到了节点 \(p\),按排名分裂的大小为 \(sz\),然后分裂讨论。
- \(siz_{ch_{p,0}}<sz\),那么说明这个节点和这个节点的左子树都属于第一棵平衡树,先向右子树递归分裂,得到二元组\((first,second)\),然后将这个节点的右儿子设置为 \(first\),然后返回 \((p,second)\)。
- \(siz_{ch_{p,0}}\ge sz\),那么说明这个节点和这个节点的右子树都属于第二棵平衡树,先向左子树递归分裂,得到二元组 \((first,second)\),然后将这个节点的左儿子设置为 \(second\),然后返回 \((first,p)\)。
pii split(int p,int sz){
if(p==0)return {0,0};//递归边界
if(sz<=Siz(ch[p][0])){
pii tmp=split(ch[p][0],sz);
ch[p][0]=tmp.second;
pushup(p);
return {tmp.first,p};
}else{
pii tmp=split(ch[p][1],sz-Siz(ch[p][0])-1);
//注意这里因为左子树和这个节点都属于第一棵平衡树,所以第一棵平衡树只剩下 sz-Siz(ch[p][0])-1 的大小了
ch[p][1]=tmp.first;
pushup(p);
return {p,tmp.second};
}
}
2.合并
这里个人感觉合并有点像左偏树的合并。
合并也一般使用递归实现,接受两个参数 \((x,y)\),表示合并以 \(x\) 为根和以 \(y\) 为根的子树,返回一个整数,表示合并之后平衡树的根。
注意这里 \(x\) 和 \(y\) 的顺序是不能互换的,如果是按值分裂的话,以 \(x\) 为根的子树中的所有权值都小于以 \(y\) 为根的子树中的任何一个权值,如果是按排名分裂的话,以 \(x\) 为根的子树中所有节点的排名都小于以 \(y\) 为根的子树中的任何一个节点的排名,否则会导致出错。
现在考虑如何合并,考虑现在要合并以 \(x\) 为根和以 \(y\) 为根的子树,然后分类讨论,注意维护堆的性质。
- \(x\) 和 \(y\) 同时为 \(0\),返回 \(0\)。
- \(x\) 和 \(y\) 中有一个为 \(0\),返回另一个非 \(0\) 值。
- \(c_x<c_y\),那么以 \(x\) 为合并后的根,然后将 \(x\) 的右儿子和 \(y\) 合并,将 \(x\) 的右儿子设为 \(x\) 的右儿子和 \(y\) 合并之后的根。
- 否则,那么以 \(y\) 为合并后的根,然后将 \(x\) 的右儿子和 \(y\) 合并,将 \(x\) 的右儿子设为 \(x\) 的右儿子和 \(y\) 合并之后的根。
int merge(int x,int y){
if(x==0&&y==0)return 0;
if(x==0)return y;
if(y==0)return x;
if(c[x]<c[y]){
ch[x][1]=merge(ch[x][1],y);
pushup(x);
return x;
}else{
ch[y][0]=merge(x,ch[y][0]);
pushup(y);
return y;
}
}
3.加入,删除一个元素。
我们已经说完了无旋 Treap 的所有基础操作,接下来我们只需要完成加入和删除操作,剩下的所有操作基本上就和有旋 Treap 都是一样的。
我们在树中加入一个值 \(v\),那么我们将平衡树按值分裂成三份,一棵中的所有权值小于 \(v\),一棵中的所有权值等于 \(v\),最后一棵中的所有权值大于 \(v\)。
显然第二棵平衡树中最多只有一个节点,如果这棵平衡树中没有节点,那么就直接新建一个节点,否则就将这个节点的 cnt 加上一,然后逐步合并回去即可。
我们在树中删除一个值 \(v\),不妨仍然假定这个值对应的节点在平衡树中必然存在,同样将平衡树按值分裂成三份,一棵中的所有权值小于 \(v\),一棵中的所有权值等于 \(v\),最后一棵中的所有权值大于 \(v\)。
然后将第二棵平衡树中的节点 \(cnt\) 减一,如果 \(cnt\) 为 \(0\),直接合并第一棵和第三棵平衡树,否则就重新将三棵平衡树合并在一起。
void insert(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(tmp2.first==0)New(tmp2.first,v);
else cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
return ;
}
void delet(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(cnt[tmp2.first]<=1)rt=merge(tmp1.first,tmp2.second);
else{
cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
}
return ;
}
4.完整代码
和有旋 Treap 一样,给出一份无旋 Treap 的完整代码实现。
struct Treap{
#define pii pair<int,int>
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num,rt;
int val[N],cnt[N],siz[N],ch[N][2];
unsigned int c[N];
mt19937 ran(time(0));
/*
rt 表示当前的根
val[p] 表示 p 节点的权值(满足 BST 性质的权值)
c[p] 表示 p 节点的随机权值(满足堆性质的权值)
cnt[p] 表示当前权值等于 val[p] 的元素有多少个
siz[p] 表示以 p 节点为根的子树中的节点个数,这里包含被合并的节点
fa[p] 表示 p 节点的父亲
ch[p][0/1] 表示 p 的左/右儿子
*/
void New(int &p,int v){
p=++num;
val[num]=v,c[p]=ran();
cnt[p]=siz[p]=1;
fa[p]=ch[p][0]=ch[p][1]=0;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
pii split(int p,int sz){
if(p==0)return {0,0};//递归边界
if(sz<=Siz(ch[p][0])){
pii tmp=split(ch[p][0],sz);
ch[p][0]=tmp.second;
pushup(p);
return {tmp.first,p};
}else{
pii tmp=split(ch[p][1],sz-Siz(ch[p][0])-1);
//注意这里因为左子树和这个节点都属于第一棵平衡树,所以第一棵平衡树只剩下 sz-Siz(ch[p][0])-1 的大小了
ch[p][1]=tmp.first;
pushup(p);
return {p,tmp.second};
}
}
int merge(int x,int y){
if(x==0&&y==0)return 0;
if(x==0)return y;
if(y==0)return x;
if(c[x]<c[y]){
ch[x][1]=merge(ch[x][1],y);
pushup(x);
return x;
}else{
ch[y][0]=merge(x,ch[y][0]);
pushup(y);
return y;
}
}
void insert(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(tmp2.first==0)New(tmp2.first,v);
else cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
return ;
}
void delet(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(cnt[tmp2.first]<=1)rt=merge(tmp1.first,tmp2.second);
else{
cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
}
return ;
}
int getMin(int p){
while(ch[p][0])p=ch[p][0];
return val[p];
}
int getMax(int p){
while(ch[p][1])p=ch[p][1];
return val[p];
}
bool search(int p,int v){
if(!p)return false;
if(val[p]==v)return true;
if(val[p]>v)return search(ch[p][0],v);
return search(ch[p][1],v);
}
int getrank(int p,int v){
if(val[p]==v)return Siz(ch[p][0]);
if(val[p]>v)return getrank(ch[p][0],v);
return getrank(ch[p][1],v)+Siz(ch[p][0])+cnt[p];
}
int getnum(int p,int rank){
if(rank<=Siz(ch[p][0]))return getnum(ch[p][0],rank);
if(rank<=Siz(ch[p][0])+cnt[p])return val[p];
return getnum(ch[p][1],rank-Siz(ch[p][0])-cnt[p]);
}
void findpre(int p,int v,int& ans){
if(!p)return ;
if(val[p]>=v)find_pre(ch[p][0],v,ans);
else{
tomax(ans,val[p]);
find_pre(ch[p][1],v,ans);
}
}
void findsuf(int p,int v,int& ans){
if(!p)return ;
if(val[p]<=v)find_suf(ch[p][1],v,ans);
else{
tomin(ans,val[p]);
find_suf(ch[p][0],v,ans);
}
}
#undef pii
#undef Siz
}
8.使用无旋 Treap 维护序列
我们使用无旋 Treap 并不仅仅只是因为无旋 Treap 好写,更大的一个原因是无旋 Treap 的用途更加广泛,其中最大的用处就是使用无旋 Treap 可以维护序列。
这里的维护,可以做到很多其他数据结构无法完成的操作,比如:区间反转,在序列的任意位置插入一个数,删除序列中的任意一个数。
这个时候 Treap 维护的不再是一个序列中的值,而是序列每个位置现在对应的原序列中的下标,而同样的,原序列中一个下标对应的节点在 Treap 中的排名,就是此时这个下标在序列中所处的位置,同样的,此时 Treap 的中序遍历序列就是此时的序列对应原序列的下标。
由于区间反转操作的存在,维护序列的无旋 Treap 常常会导致一个十分难以理解的问题:Treap 的点权不再满足 BST 的性质了,也就是说,现在的 Treap 只满足平衡性了,请在阅读后文的过程中时刻注意这一点。
下文使用的 Treap 均以上文中给出的无旋 Treap 完整代码为基础,将其中的分裂方式换成按排名分裂,在其中增加若干函数和变量得到。
0.无旋 Treap 维护序列的基本逻辑
首先,无旋 Treap 要对一个区间进行操作的第一步,就是将这个区间从整棵平衡树中分裂出来,这里能且只能使用按排名分裂(忘记按排名分裂是什么可以往回翻看),因为此时点权不满足 BST 的性质了,按值分裂显然出锅。
使用按排名分裂其实是直观且好理解的,正如我们在前面说的一样:原序列中一个下标对应的节点在 Treap 中的排名,就是此时这个下标在序列中所处的位置。
所以对于一个操作区间 \([l,r]\),我们可以先在原平衡树中分裂出前 \(l-1\) 个数,然后在分裂出的第二棵平衡树中分裂出前 \(r-l+1\) 个数,形成新的第二和第三棵平衡树,那么中间那棵平衡树就是我们需要的,代表了操作区间的那棵平衡树,接下来的操作,我们都只需要在这棵平衡树上操作即可。
操作完之后(通常就是直接打个标签的事),我们再将三棵平衡树合并到一起即可。
1.区间反转
由于中序遍历序列就是此时的序列对应原序列的下标,我们只需要想方设法反转中序遍历即可。
方法似乎显然,我们只需要反转平衡树中每一个节点的左右子树即可,具体实现可以使用懒惰标记,表示现在这个节点的子树需不需要反转,每一次下传时如果需要反转,那么反转左右子树,然后将标记向下传递即可。
2.插入、删除一个节点
显然,按排名分裂后进行对应操作即可。
3.区间加,乘
使用懒惰标记进行修改,维护区间和时注意:需要合并的区间实际上有三个,左子树对应的区间,当前节点对应的长度唯一的区间,右子树对应的区间。
4.模板题及其示例代码
struct Treap{
#define pii pair<int,int>
#define Siz(x) (x==0?0:siz[x])//防止 0 这个节点进行了一些奇奇怪怪的操作
int num,rt;
int val[N],cnt[N],siz[N],ch[N][2];
unsigned int c[N];
bool tag[N];
mt19937 ran(time(0));
/*
rt 表示当前的根
val[p] 表示 p 节点的权值(满足 BST 性质的权值)
c[p] 表示 p 节点的随机权值(满足堆性质的权值)
cnt[p] 表示当前权值等于 val[p] 的元素有多少个
siz[p] 表示以 p 节点为根的子树中的节点个数,这里包含被合并的节点
fa[p] 表示 p 节点的父亲
ch[p][0/1] 表示 p 的左/右儿子
*/
void New(int &p,int v){
p=++num;
val[num]=v,c[p]=ran();
cnt[p]=siz[p]=1;
fa[p]=ch[p][0]=ch[p][1]=0;
}
void pushup(int p){
siz[p]=Siz(ch[p][0])+Siz(ch[p][1])+cnt[p];
if(ch[p][0])fa[ch[p][0]]=p;
if(ch[p][1])fa[ch[p][1]]=p;
fa[p]=0;
}
void pushdown(int p){
if(!tag[p])return ;
swap(ch[p][0],ch[p][1]);
if(ch[p][0])tag[ch[p][0]]^=1;
if(ch[p][1])tag[ch[p][1]]^=1;
tag[p]=0;
}
pii split(int p,int sz){
if(p==0)return {0,0};
pushdown(p);
if(sz<=Siz(ch[p][0])){
pii tmp=split(ch[p][0],sz);
ch[p][0]=tmp.second;
pushup(p);
return {tmp.first,p};
}else{
pii tmp=split(ch[p][1],sz-Siz(ch[p][0])-1);
ch[p][1]=tmp.first;
pushup(p);
return {p,tmp.second};
}
}
int merge(int x,int y){
if(x==0&&y==0)return 0;
if(y==0)return x;
if(x==0)return y;
pushdown(x),pushdown(y);
if(c[x]<c[y]){
ch[x][1]=merge(ch[x][1],y);
pushup(x);
return x;
}else{
ch[y][0]=merge(x,ch[y][0]);
pushup(y);
return y;
}
}
void insert(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(tmp2.first==0)New(tmp2.first,v);
else cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
return ;
}
void delet(int v){
pii tmp1=split(rt,v-1);
pii tmp2=split(tmp1.second,v);
if(cnt[tmp2.first]<=1)rt=merge(tmp1.first,tmp2.second);
else{
cnt[tmp2.first]++;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
}
return ;
}
void change(int l, int r) {
pii tmp1=split(rt,l-1);
pii tmp2=split(tmp1.second,r-l+1);
tag[tmp2.first]=1;
rt=merge(tmp1.first,merge(tmp2.first,tmp2.second));
return ;
}
#undef pii
#undef Siz
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号