虚树学习笔记

定义

虚树（Virtual Tree）：询问点与其 LCA 组成的树。

性质

假设询问点只有 \(k\) 个，那么虚树最多只含有 \(2k - 1\) 个结点。

这一性质使得我们能够排除很多无用状况，减小时间复杂度。

建树：单调栈建树

类似笛卡尔树，我们用一个栈来维护当前的右链，不过不同的是，这里的右链都是还未加入虚树的节点。

在栈加入根节点 \(rt\)。
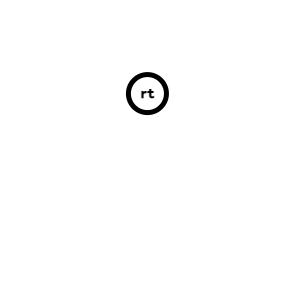
按 DFS 序不断往栈中加入节点与栈顶元素的 LCA 和其本身。

那么加入时，大致会碰到两种情况：
- LCA 就是栈顶元素，则当前节点在栈顶元素的子树中，那么直接加入当前节点即可。
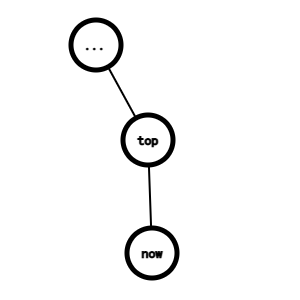
- LCA 不是栈顶元素，那么我们需要不断退栈，直到其次栈顶元素深度小于等于 LCA。
  
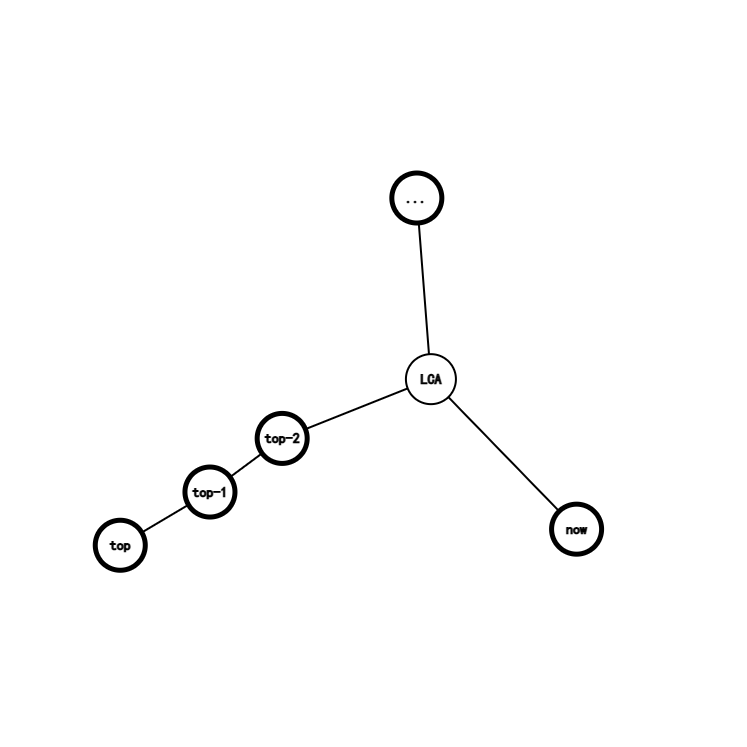
  注意：退栈过程中，如果栈中元素个数超过 1，那么我们往虚树中加入一条连接栈顶元素与次栈顶元素的边。
  
  那么退栈结束后，因为 LCA 可能并不在我们维护的右链中，所以我们需要先连一条栈顶元素和 LCA 的边，以保证虚树的正确性，再把栈顶元素退栈，接下来只剩两种可能：
  1. 栈顶元素为 LCA：那么直接加入当前元素；
  2. 栈顶元素不为 LCA：加入 LCA 后再加入当前元素。
所有节点都加入后，重复退栈连边，直至栈中只剩根节点 \(rt\)。

时间复杂度瓶颈在于排序与求 LCA，可以做到 \(O(n\log_2{n})\) 或 \(O(n)\)。

清空

在清空虚树时，我们要注意不能直接在原树上扫过去，否则复杂度就退化成 \(O(n)\) 的了。我们可以开一个数组存虚树上的点，最后全部清空即可。

应用

P2495 [SDOI2011] 消耗战

一道非常经典的例题，这道题属于虚树模版，建完树后只需要做一个十分简单的树形 DP 即可：

设当前点 \(u\) 到根上的最小边权为 \(pa_u\)，DP 数组为 \({\{ f_u \}}_1^n\)。

当前点为询问点（资源所在点），那么直接返回当前点到根上的最小边权即可；

\[f_u = pa_u \\ \]
否则向下 DFS，求得虚树上个子节点的 DP 值之和，与当前点到根上的最小边权取最小值再返回。

\[f_u = \min(\sum_{v \in son_u} f_v,pa_u) \\ \]

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f
#define ll long long
#define RCL(a,b,c,d) memset(a,b,sizeof(c)*(d))
#define FOR(i,a,b) for(int i(a);i<=(int)(b);++i)
#define DOR(i,a,b) for(int i(a);i>=(int)(b);--i)
#define tomax(a,...) ((a)=max({(a),__VA_ARGS__}))
#define tomin(a,...) ((a)=min({(a),__VA_ARGS__}))
#define EDGE(g,i,x,y) for(int i=(g).h[(x)],y=(g)[(i)].v;~i;y=(g)[i=(g)[i].nxt].v)
#define main Main();signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);return Main();}signed Main
using namespace std;
constexpr int N=2.5e5+10,lN=18,lV=lN+1;
namespace Virtual_Tree {
	bool mark[N];
	int n,idx;
	int dl[N],dr[N],fa[N],Lg[N],pa[N],dfn[N],dep[N];
	int dlca[N][lV];
	template<const int N,const int M>struct CFS {
		int tot,h[N];
		struct edge {
			int v,w,nxt;
			edge(int v=0,int w=0,int nxt=-1):v(v),w(w),nxt(nxt) {}
		} e[M];
		edge &operator[](int i) {
			return e[i];
		}
		void Init(int n) {
			tot=-1,RCL(h+1,-1,int,n);
		}
		void Clear(const vector<int> &tmp) {
			tot=-1;
			for(const int &x:tmp)h[x]=-1;
		}
		void att(int u,int v,int w=0) {
			e[++tot]=edge(v,w,h[u]),h[u]=tot;
		}
		void con(int u,int v,int w=0) {
			att(u,v,w),att(v,u,w);
		}
	};
	CFS<N,N<<1> g;
	CFS<N,N> G;
	void dfs0(int u) {
		dfn[dl[u]=++idx]=u,dep[u]=dep[dlca[dl[u]][0]=fa[u]]+1;
		EDGE(g,i,u,v)if(v^fa[u])pa[v]=min(g[i].w,pa[fa[v]=u]),dfs0(v);
		dr[u]=idx;
	}
	int dmin(int u,int v) {
		return dl[u]<dl[v]?u:v;
	}
	int lca(int u,int v) {
		if(u==v)return u;
		if((u=dl[u])>(v=dl[v]))swap(u,v);
		int x=Lg[v-u++];
		return dmin(dlca[u][x],dlca[v-(1<<x)+1][x]);
	}
	void Build() {
		cin>>n,g.Init(n),G.Init(n),Lg[0]=-1;
		FOR(i,1,n)Lg[i]=Lg[i>>1]+1;
		FOR(i,2,n) {
			int u,v,w;
			cin>>u>>v>>w,g.con(u,v,w);
		}
		pa[1]=INF,dfs0(1);
		FOR(j,1,lN)FOR(i,1,n-(1<<j)+1)dlca[i][j]=dmin(dlca[i][j-1],dlca[i+(1<<(j-1))][j-1]);
	}
	vector<int> Rebuild(vector<int> &Que) {
		static int top(0);
		static int st[N];
		vector<int> tmp;
		sort(Que.begin(),Que.end(),[&](int x,int y) {
			return dl[x]<dl[y];
		});
		tmp.push_back(st[top=1]=dfn[1]);
		for(const int &u:Que) {
			mark[u]=1;
			int pa=lca(u,st[top]);
			if(pa!=st[top]) {
				while(top>1&&dep[st[top-1]]>dep[pa])G.att(st[top-1],st[top]),--top;
				G.att(pa,st[top]),--top;
			}
			if(st[top]!=pa)st[++top]=pa,tmp.push_back(pa);
			if(st[top]!=u)st[++top]=u,tmp.push_back(u);
		}
		while(top>1)G.att(st[top-1],st[top]),--top;
		return tmp;
	}
	ll dfs1(int u) {
		ll sum(0);
		if(mark[u])return pa[u];
		EDGE(G,i,u,v)sum+=dfs1(v);
		return min(sum,u==1?LINF:(ll)pa[u]);
	}
	ll Query(vector<int> &Que) {
		vector<int> tmp(Rebuild(Que));
		ll ans(dfs1(1));
		G.Clear(tmp);
		for(const int &x:Que)mark[x]=0;
		return tmp.clear(),Que.clear(),ans;
	}
} using namespace Virtual_Tree;
int Q;
signed main() {
	for(Build(),cin>>Q; Q; --Q) {
		int k,x;
		vector<int> cur;
		cin>>k;
		FOR(i,1,k)cin>>x,cur.push_back(x);
		cout<<Query(cur)<<endl;
	}
	return 0;
}

P10930 异象石

注：这题是多倍经验。

这题是让我们维护一个动态的树上路径并。

首先，树上路径并我们可以用虚树来求，所以如果有部分分的话，可以暴力建虚树来处理。

假设我们要求的虚树上的路径点集按照 DFS 序排好序后为 \(\{ a_i \}_1^n\)，那么我们所求的值即为：

\[\frac{\sum_{i=1}^{n}dis(a_i,a_{((i+1) \bmod n)+1})}2 \]

但是直接这么做非常麻烦，我们把式子化简一下：

\[\begin{aligned} \frac{\sum_{i=1}^{n}dis(a_i,a_{((i+1) \bmod n)+1})}2 & = \frac{\sum_{i=1}^{n}dis_{a_i}+dis_{a_{((i+1) \bmod n)+1}}-2dis_{lca(a_i,a_{((i+1) \bmod n)+1})}}2 \\ & = \sum_{i=1}^n dis_{a_i} - \sum_{i=1}^{n} dis_{lca(a_i,a_{((i+1) \bmod n)+1})} \end{aligned} \]

那么剩下的就非常简单了，用一个 set<int> 实现动态维护即可。

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define RCL(a,b,c,d) memset(a,b,sizeof(c)*(d))
#define FOR(i,a,b) for(int i(a);i<=(int)(b);++i)
#define DOR(i,a,b) for(int i(a);i>=(int)(b);--i)
#define tomax(a,...) ((a)=max({(a),__VA_ARGS__}))
#define tomin(a,...) ((a)=min({(a),__VA_ARGS__}))
#define EDGE(g,i,x,y) for(int i=(g).h[(x)],y=(g)[(i)].v;~i;y=(g)[i=(g)[i].nxt].v)
#define main Main();signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);return Main();}signed Main
using namespace std;
constexpr int N=1e5+10,lN=17,lV=lN+1;
namespace Tree {
	int n,idx;
	int dl[N],Lg[N],dep[N],dfn[N];
	int dlca[N][lV];
	ll dis[N];
	template<const int N,const int M>struct CFS {
		int tot,h[N];
		struct edge {
			int v,w,nxt;
			edge(int v=0,int w=0,int nxt=-1):v(v),w(w),nxt(nxt) {}
		} e[M];
		edge &operator[](int i) {
			return e[i];
		}
		void Init(int n) {
			tot=-1,RCL(h+1,-1,int,n);
		}
		void att(int u,int v,int w) {
			e[++tot]=edge(v,w,h[u]),h[u]=tot;
		}
		void con(int u,int v,int w) {
			att(u,v,w),att(v,u,w);
		}
	};
	CFS<N,N<<1> g;
	void dfs(int u,int fa) {
		dep[dfn[dl[u]=++idx]=u]=dep[fa]+1,dlca[dl[u]][0]=fa;
		EDGE(g,i,u,v)if(v^fa)dis[v]=dis[u]+g[i].w,dfs(v,u);
	}
	int dmin(int u,int v) {
		return dl[u]<dl[v]?u:v;
	}
	int lca(int u,int v) {
		if(u==v)return u;
		if((u=dl[u])>(v=dl[v]))swap(u,v);
		int x=Lg[v-u++];
		return dmin(dlca[u][x],dlca[v-(1<<x)+1][x]);
	}
	void Build() {
		cin>>n,g.Init(n),Lg[0]=-1;
		FOR(i,1,n)Lg[i]=Lg[i>>1]+1;
		FOR(i,2,n) {
			int u,v,w;
			cin>>u>>v>>w,g.con(u,v,w);
		}
		dfs(1,0);
		FOR(j,1,lN)FOR(i,1,n-(1<<j)+1)dlca[i][j]=dmin(dlca[i][j-1],dlca[i+(1<<(j-1))][j-1]);
	}
} using namespace Tree;
namespace VT {
	int Q;
	ll sum;
	set<int> st;
	int Pre(int u) {
		if(st.empty())return dfn[u];
		auto it=st.lower_bound(u);
		return dfn[it==st.begin()?*st.rbegin():*--it];
	}
	int Nxt(int u) {
		if(st.empty())return dfn[u];
		auto it=st.upper_bound(u);
		return dfn[it==st.end()?*st.begin():*it];
	}
	void Insert(int u) {
		int pre(Pre(dl[u])),nxt(Nxt(dl[u]));
		sum+=dis[u]-dis[lca(pre,u)]-dis[lca(u,nxt)]+dis[lca(pre,nxt)],st.insert(dl[u]);
	}
	void Erase(int u) {
		st.erase(dl[u]);
		int pre(Pre(dl[u])),nxt(Nxt(dl[u]));
		sum-=dis[u]-dis[lca(pre,u)]-dis[lca(u,nxt)]+dis[lca(pre,nxt)];
	}
	void Operate() {
		for(cin>>Q; Q; --Q) {
			char opt;
			int u;
			cin>>opt;
			if(opt=='+')cin>>u,Insert(u);
			else if(opt=='-')cin>>u,Erase(u);
			else cout<<sum<<endl;
		}
	}
} using namespace VT;
signed main() {
	Build(),Operate();
	return 0;
}

总结

虚树主要的用途就是按照询问缩小处理范围以减小时间复杂度以及求树上路径并，做题的时候可能会碰到一些套路，要多加注意。

posted @ 2024-09-28 15:48 Add_Catalyst 阅读(201) 评论(0) 收藏举报

刷新页面返回顶部

珈猫的小窝

欢迎来到珈猫的小窝

虚树学习笔记

虚树学习笔记

定义

性质

建树：单调栈建树

清空

应用

P2495 [SDOI2011] 消耗战

P10930 异象石

总结

公告