P9907 [COCI 2023/2024 #1] Mostovi 题解

前言

一道挺考察综合能力的题目，代码能力和分析能力都很有体现。

题意分析

在去除原题一大段废话后，题意就十分明确了，洛谷的题面也是直接告诉我们了：给定一张 \(n\) 个点 \(m\) 条边的无向连通图，求有多少条边满足删去这条边两端的两个点之后，剩余的 \(n-2\) 个点不连通。

思路

部分分

第 1、2 两个子任务：用并查集维护；
第 3 个子任务：我真不知道怎么写……
第 4 个子任务：因为 DFS 树上非树边较少，可以枚举边，然后进行一系列操作（我们老师讲的，我当时直接懵逼了，所以不保证正确性）。

正解（大致思路）

首先，我们很容易想到要建一棵 DFS 树，然后边就分成了树边与非树边。

分类讨论：（合法是指：删除后剩余的 \(n-2\) 个点连通，与题目相反）

非树边：

我们再来画一个非常直观的图（只包括树边）：

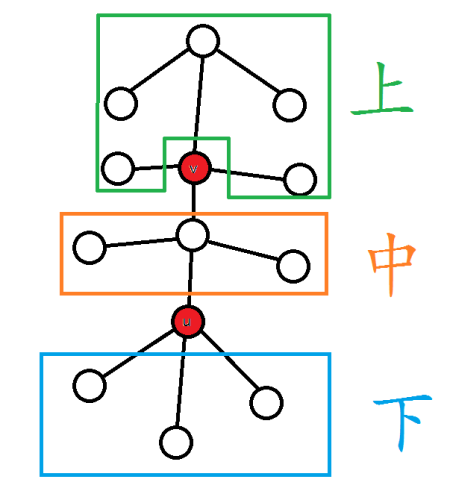
假设我们现在选了一条非树边，是连接 \(u\) 与 \(v\) 的（其中 \(v\) 的深度更小），我们将它们删除，树就变成了图中的样子（“上”、“下”两部分可能不存在），那么现在的思路就很清晰，我们只要分类讨论就可以得出结果：
1. 没有“上”部分（\(v\) 为树根）：当且仅当根的子节点数 \(\le1\)，删除合法；
2. “上”部分自己不联通：删除不合法；
3. 当“下”部分（“下”部分存在）中有任意一棵子树无法连接到“上”与“中”部分：删除不合法；
4. “下”部分中所有子树都只能够与“上”、“中”其中一部分连接或者没有“下”部分：此时当且仅当“中”部分与“上”部分能够连接，删除合法。
5. “下”部分中有任意一棵子树能够同时与“上”、“中”两部分连接：删除合法；
树边：（可以视作“非树边”部分中没有“中”部分）

我们设一条树边连接 \(u\) 与 \(v\) ，其中 \(v\) 是 \(u\) 的父节点，那么依然是分类讨论：
1. \(v\) 为根：考虑根的子节点数，
  1. 只有一个子节点：当且仅当 \(u\) 的子节点数 \(\le 1\)，删除合法；
  2. 有两个子节点：当且仅当 \(u\) 的子节点数 \(= 0\)，删除合法；
  3. 有两个以上子节点：删除不合法；
2. \(v\) 不为根：那么显而易见，要求删除 \(u\)，\(v\) 后，以他们所有剩余子节点为根的子树都有连到 \(v\) 上方的边，删除合法。

在建树之后，就会发现一个非常有用的性质：树上的非树边全都是返祖边，也就是从某个节点连到自己的祖先上，利用这个性质，我们可以方便地把非树边的另一端转换成深度，并进行记录。

对于上方的各个讨论结果，我们一个一个来看他们的解决方案：

非树边（\(u\) 到 \(v\)，其中 \(v\) 的深度更小）：
1. 没有“上”部分（\(v\) 为树根）：记录一下根的子节点数即可轻松判断；
2. “上”部分自己不联通：记录以 \(v\) 的子节点为根的子树中有几棵无法连接到 \(v\) 的祖先上，如果这个数 \(>1\)，删除不合法；
3. “下”部分（“下”部分存在）中有任意一棵子树无法连接到“上”与“中”部分：用树上 DP 解决，同时用一个 STL::map 维护特殊情况：某棵子树只有一条连到 \(u\) 的祖先上的边，那么当另一端被删除，这棵子树就独立出来了，删除不合法；
4. “下”部分中所有子树都只能够与“上”、“中”其中一部分连接或者没有“下”部分：我们可以倍增处理后“中”部分能够到达的最小深度，然后进行判断即可。
5. “下”部分中有任意一棵子树能够同时与“上”、“中”两部分连接：我们可以记录下所有以 \(u\) 的子节点为根的子树能够到达的深度最小值与小于 \(u\) 的深度的最小值，设为 \(l,r\)，判断 \(v\) 的深度是否处在其中任意一个开区间 \((l_i,r_i)\) 中，如果是，删除合法，这里可以用各种合并方法。
树边（\(v\) 是 \(u\) 的父节点）：
1. \(v\) 为根：只要记录所有节点的子节点数即可方便判断；
2. \(v\) 不为根：记录以 \(v\) 的子节点为根的子树中有几棵无法连接到 \(v\) 的祖先上，再分类：
  1. 如果这个数 \(>1\)，删除不合法；
  2. 如果这个数 \(=1\)，当且仅当无法连接到 \(v\) 的祖先上的子树的根为 \(u\)，同时 \(u\) 是叶子节点，删除合法；
  3. 如果这个数 \(=0\)，删除合法。

提示：分类讨论的顺序很重要，好的顺序可以规避错误与节省精力。

代码实现

启发式合并做法：

//#define Local
#include<algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#define INF 0x3f3f3f3f
#define F first
#define S second
#define Pii pair<int,int>
#define min(a,b) ((a)>(b)?(b):(a))
#define tomin(a,b) ((a)=min((a),(b)))
#define FOR(i,a,b) for(register int i=(a);i<=(b);++i)
#define DOR(i,a,b) for(register int i=(a);i>=(b);--i)
#define EDGE(g,i,u,v) for(register int (i)=(g).h[(u)],(v)=(g).v[(i)];(i);(i)=(g).nxt[(i)],(v)=(g).v[(i)])
#define main Main();signed main(){ios::sync_with_stdio(0);cin.tie(0);return Main();}signed Main
using namespace std;
namespace IO {
#ifndef Local
	inline char gc() {
		static char BB[1000001],*S=BB,*T=BB;
		return S==T&&(T=(S=BB)+fread(BB,1,1000000,stdin),S==T)?(EOF):*S++;
	}
#endif

#ifdef Local
#define gc() getchar()
#endif

	template<typename T>
	inline void rd(T& x) {
		int w=1;
		x=0;
		char ch=gc();
		while((ch<'0'||ch>'9')&&ch!=((EOF))) {
			if(ch=='-')w=-1;
			ch=gc();
		}
		while(ch>='0'&&ch<='9')
			x=(x<<3)+(x<<1)+(ch^48),ch=gc();
		x*=w;
		return;
	}
	template <typename T>
	void write(T x) {
		if(x<0)putchar('-'),x=-x;
		if(x>9)write(x/10);
		putchar(x%10+'0');
	}
	template <typename T>
	inline void wr(T x,char End='\n') {
		write(x),putchar(End);
	}
}
using namespace IO;
const int N=1e5+10,M=3e5+10,lV=19,lN=17;
bool vis[N];
int n,m,ans;
int fa[N][lV];
set<int> st[N];
vector<int> son[N];
int dep[N],sum[N],id[N];
struct Chain_Forward_Star { //链式前向星
	int tot,v[M<<1],nxt[M<<1],h[N];
	inline void att(int U,int V) {
		v[++tot]=V,nxt[tot]=h[U],h[U]=tot;   //加入单向边
	}
	inline void con(int U,int V) {
		att(V,U),att(U,V);   //加入双向边
	}
} g;
struct node {
	int x,y;
	node() {
		x=y=INF;
	}
	inline void merge(int val) {
		if(val==x)return;
		if(val<x)y=x,x=val;
		else tomin(y,val);
	}
	inline void merge(const node &b) {
		merge(b.x),merge(b.y);
	}
	friend node merge(node a,const node &b) {
		a.merge(b);
		return a;
	}
} f[N][lV],s[N],pos[N];
/*
本题有多处用到最小/严格次小值，
为了方便，我们在此处开一个结构体node，保存最小与严格次小值，
从本题代码中，我们也能够看出，它确实便利了我们很多.
*/
/*
变量说明:
n，m:如题目所述；
ans:满足删去这条边两端的两个点之后，剩余的n-2个点连通的个数(与题目描述相反，便于判断)；
fa[u][i]:u的2^i级祖先；
STL::set st[u]数组:用于启发式合并该子树中能够到达上方的所有边的深度；
dep[u]:u在DFS树中的深度；
sum[u]:以u的子节点为根的子树中，有几棵没有能够连到u的祖先上的边，id[u]记的是这类子节点中任意一个；
STL::vector son[u]数组:在DFS树上，u的子节点；
g:链式前向星，用于存图；
f[u][i]:去掉以u为根的这棵子树后，以u的2^i级祖先为根的树中的边能够向上到达的最小/严格次小深度；
s[u]:以u为根的这棵子树中的边能够向上到达的最小/严格次小深度；
pos[u]:u上的非树边能够向上到达的最小/严格次小深度；
*/
void dfs1(int u) {
	vis[u]=1,dep[u]=dep[fa[u][0]]+1;
	vector<node> lmx,rmx;//存下以子节点的根的这子树中的边能够向上到达的最小/严格次小深度
	EDGE(g,i,u,v)if(v!=fa[u][0]) {
		if(!vis[v]) {
			fa[v][0]=u,dfs1(v);
			s[u].merge(s[v]),lmx.emplace_back(s[v]),rmx.emplace_back(s[v]);
			son[u].emplace_back(v);
			if(s[v].x>=dep[u])++sum[u],id[u]=v;
		} else pos[u].merge(dep[v]);
	}
	if(!son[u].empty()) {
		int sons=son[u].size();
		FOR(i,1,sons-1)lmx[i].merge(lmx[i-1]);
		//前缀处理，此时其含义变成以1~i个子节点的根的这子树中的边能够向上到达的最小/严格次小深度
		DOR(i,sons-2,0)rmx[i].merge(rmx[i+1]);
		//后缀处理，此时其含义变成以i~son[u].size()个子节点的根的这子树中的边能够向上到达的最小/严格次小深度
		FOR(i,0,sons-1) {
			int v=son[u][i];
			if(i)f[v][0].merge(lmx[i-1]);//i之前的最小/严格次小深度
			if(i+1<sons)f[v][0].merge(rmx[i+1]);//i之后的最小/严格次小深度
		}
	}
	s[u].merge(pos[u]);//和以u为根的这棵子树中的边能够向上到达的最小/严格次小深度
	lmx.clear(),rmx.clear();
}/*第一遍DFS:建出DFS树，更新s[u]，pos[u]，f[u][0]*/
void dfs2(int u) {
	f[u][0].merge(pos[fa[u][0]]);
	FOR(i,1,lN)
	fa[u][i]=fa[fa[u][i-1]][i-1],f[u][i]=merge(f[u][i-1],f[fa[u][i-1]][i-1]);
	for(int v:son[u])dfs2(v);
}/*第二遍DFS:倍增更新f[u][i]*/
void dfs3(int u) {
	map<int,bool> h;//用于标记哪些深度会让图不连通
	set< Pii > ST;//记录该子树能够到达的最大与最小深度
	bool flag=0;
	for(int v:son[u]) {
		dfs3(v);
		while(!st[v].empty()&&(*st[v].rbegin())>=dep[u])st[v].erase(prev(st[v].end()));//去掉深度不合法的
		if(st[v].size()>1)ST.insert({*st[v].rbegin(),*st[v].begin()});
		if(st[v].size()>st[u].size())swap(st[u],st[v]);//交换地址:O(1)
		for(int x:st[v])st[u].insert(x);
		st[v].clear();//进行启发式合并
		if(s[v].x>=dep[u]&&(flag=1))continue;//以该子节点为根的子树中的边没有能达到u的祖先的
		if(s[v].y>=dep[u])h[s[v].x]=1;
		//以该子节点为根的子树中的边只有一条能达到u的祖先，此时删去该祖先会让图不连通
	}
	vector< Pii > l(ST.begin(),ST.end());
	ST.clear();
	int tot=l.size();
	DOR(i,tot-2,0)tomin(l[i].S,l[i+1].S);//后缀处理
	EDGE(g,i,u,v) {
		if(dep[v]>dep[u])continue;//排除无用边
		st[u].insert(dep[v]);//加入集合
		if(v==1) {
			if(sum[v]!=1) {
				if(sum[v]==2&&son[u].empty()&&v==fa[u][0])++ans;//该边为树边并且合法
				continue;
			}
			if(1==fa[u][0]&&son[u].size()!=1)continue;//该边为树边但不合法
			if(1!=fa[u][0]&&(h.count(1)||flag))continue;//该边为非树边但不合法
			++ans;
			continue;
		}//没有“上”部分，v为根
		if(flag)continue;
		if(v!=fa[u][0]) {
			node t;
			int x=u;
			DOR(i,lN,0)if((dep[x]-(1<<i)>dep[v]))t.merge(f[x][i]),x=fa[x][i];
			//求出“中”部分能够到达的最小深度
			if(t.x>=dep[v]) {
				auto it=upper_bound(l.begin(),l.end(),make_pair(dep[v],INF));
				if(it==l.end()||(it->second)>=dep[v])continue;
				//“下”部分中没有任意一棵子树能够同时与“上”、“中”两部分连接
			}
		}//判断非树边
		if(sum[v]>1||sum[v]&&(u!=id[v])||h.count(dep[v]))continue;
		if(!sum[v]||!son[u].size())++ans;
	}
	h.clear(),l.clear();
}/*第三遍DFS:求出答案*/
signed main() {
	rd(n),rd(m);
	FOR(i,1,m) {
		int u,v;
		rd(u),rd(v);
		g.con(u,v);
	}
	dfs1(1),dfs2(1),dfs3(1);
	wr(m-ans);
	return 0;
}

我在此使用的是启发式合并，它是该算法的时间复杂度瓶颈。

时间复杂度应是：约 \(O(m \log^2{m})\) （视 \(n,m\) 同级，下同），但是由于启发式合并用了 STL::set ，其中记的又是深度，所以是完全跑不到满的，甚至比一些时间复杂度更小的还要快。

实际最快用时：584ms，内存：64.99MB。

优化

如果仅是优化理论时间复杂度，那么可以用左偏树合并，但是实际跑起来可能会慢一点。

//#define Local
#include<algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#define INF 0x3f3f3f3f
#define F first
#define S second
#define Pii pair<int,int>
#define min(a,b) ((a)>(b)?(b):(a))
#define tomin(a,b) ((a)=min((a),(b)))
#define FOR(i,a,b) for(register int i=(a);i<=(b);++i)
#define DOR(i,a,b) for(register int i=(a);i>=(b);--i)
#define EDGE(g,i,u,v) for(register int (i)=(g).h[(u)],(v)=(g).v[(i)];(i);(i)=(g).nxt[(i)],(v)=(g).v[(i)])
#define main Main();signed main(){ios::sync_with_stdio(0);cin.tie(0);return Main();}signed Main
using namespace std;
namespace IO {
#ifndef Local
	inline char gc() {
		static char BB[1000001],*S=BB,*T=BB;
		return S==T&&(T=(S=BB)+fread(BB,1,1000000,stdin),S==T)?(EOF):*S++;
	}
#endif

#ifdef Local
#define gc() getchar()
#endif

	template<typename T>
	inline void rd(T& x) {
		int w=1;
		x=0;
		char ch=gc();
		while((ch<'0'||ch>'9')&&ch!=((EOF))) {
			if(ch=='-')w=-1;
			ch=gc();
		}
		while(ch>='0'&&ch<='9')
			x=(x<<3)+(x<<1)+(ch^48),ch=gc();
		x*=w;
		return;
	}
	template <typename T>
	void write(T x) {
		if(x<0)putchar('-'),x=-x;
		if(x>9)write(x/10);
		putchar(x%10+'0');
	}
	template <typename T>
	inline void wr(T x,char End='\n') {
		write(x),putchar(End);
	}
}
using namespace IO;
const int N=1e5+10,M=3e5+10,lV=19,lN=17;
bool vis[N];
int n,m,ans;
int fa[N][lV];
int rt[N];
struct Leftist_Heap {
	int n;
	struct node {
		int val,id,ch[2],d,fa;
		int & operator [](bool x) {
			return ch[x];
		}
		friend bool operator <(node a,node b) {
			return a.val!=b.val?a.val<b.val:a.id<b.id;
		}
		friend bool operator >(node a,node b) {
			return b<a;
		}
	} t[M];
	/**/
	inline int& rs(int x) {
		return t[x][t[t[x][1]].d < t[t[x][0]].d];
	}
	inline int& ls(int x) {
		return t[x][t[t[x][1]].d >= t[t[x][0]].d];
	}
	/**/
	int merge(int x,int y) {
		if(!x||!y)return (x|y);
		if(t[x]<t[y])swap(x,y);
		t[rs(x)=merge(rs(x),y)].fa=x;
		t[x].d=t[rs(x)].d+1;
		return x;
	}
	inline int Insert(int val,int x) {
		t[++n]= {val,n,{0,0},1,0};
		return x?merge(n,x):n;
	}
	inline int Del(int x) {
		int p=merge(ls(x),rs(x));
		return t[p].fa=0,p;
	}
} lt;
vector<int> son[N];
int dep[N],sum[N],id[N];
struct Chain_Forward_Star {
	int tot,v[M<<1],nxt[M<<1],h[N];
	inline void att(int U,int V) {
		v[++tot]=V,nxt[tot]=h[U],h[U]=tot;
	}
	inline void con(int U,int V) {
		att(V,U),att(U,V);
	}
} g;
struct node {
	int x,y;
	node() {
		x=y=INF;
	}
	inline void merge(int val) {
		if(val==x)return;
		if(val<x)y=x,x=val;
		else tomin(y,val);
	}
	inline void merge(const node &b) {
		merge(b.x),merge(b.y);
	}
	friend node merge(node a,const node &b) {
		a.merge(b);
		return a;
	}
} f[N][lV],s[N],pos[N];
void dfs1(int u) {
	vis[u]=1,dep[u]=dep[fa[u][0]]+1;
	node lmx;
	vector<node> rmx;
	EDGE(g,i,u,v)if(v!=fa[u][0]) {
		if(!vis[v]) {
			fa[v][0]=u,dfs1(v);
			if(!son[u].empty())f[v][0].merge(lmx);
			s[u].merge(s[v]),lmx.merge(s[v]),rmx.emplace_back(s[v]);
			son[u].emplace_back(v);
			if(s[v].x>=dep[u])++sum[u],id[u]=v;
		} else pos[u].merge(dep[v]);
	}
	DOR(i,son[u].size()-2,0)rmx[i].merge(rmx[i+1]),f[son[u][i]][0].merge(rmx[i+1]);
	s[u].merge(pos[u]);
	rmx.clear();
}
void dfs2(int u) {
	f[u][0].merge(pos[fa[u][0]]);
	FOR(i,1,lN)
	fa[u][i]=fa[fa[u][i-1]][i-1],f[u][i]=merge(f[u][i-1],f[fa[u][i-1]][i-1]);
	for(int v:son[u])dfs2(v);
}
void dfs3(int u) {
	map<int,bool> h;
	set< Pii > ST;
	bool flag=0;
	for(int v:son[u]) {
		dfs3(v);
		while(rt[v]&&lt.t[rt[v]].val>=dep[u])rt[v]=lt.Del(rt[v]);
		if(rt[v])ST.insert({lt.t[rt[v]].val,s[v].x});
		rt[u]=rt[u]?lt.merge(rt[u],rt[v]):rt[v];
		if(s[v].x>=dep[u]&&(flag=1))continue;
		if(s[v].y>=dep[u])h[s[v].x]=1;
	}
	vector< Pii > l(ST.begin(),ST.end());
	ST.clear();
	int tot=l.size();
	DOR(i,tot-2,0)tomin(l[i].S,l[i+1].S);
	EDGE(g,i,u,v) {
		if(dep[v]>dep[u])continue;
		rt[u]=lt.Insert(dep[v],rt[u]);
		if(v==1) {
			if(sum[v]!=1) {
				if(sum[v]==2&&son[u].empty()&&1==fa[u][0])++ans;
				continue;
			}
			if(1==fa[u][0]&&son[u].size()!=1)continue;
			if(1!=fa[u][0]&&(h.count(1)||flag))continue;
			++ans;
			continue;
		}
		if(flag)continue;
		if(v!=fa[u][0]) {
			node t;
			int x=u;
			DOR(i,lN,0)if((dep[fa[x][i]]>dep[v]))t.merge(f[x][i]),x=fa[x][i];
			if(t.x>=dep[v]) {
				auto it=upper_bound(l.begin(),l.end(),make_pair(dep[v],INF));
				if(it==l.end()||(it->second)>=dep[v])continue;
			}
		}
		if(sum[v]>1||sum[v]&&(u!=id[v])||h.count(dep[v]))continue;
		if(!sum[v]||!son[u].size())++ans;
	}
	h.clear(),l.clear();
}
signed main() {
	rd(n),rd(m);
	FOR(i,1,m) {
		int u,v;
		rd(u),rd(v);
		g.con(u,v);
	}
	dfs1(1),dfs2(1),dfs3(1);
	wr(m-ans);
	return 0;
}

时间复杂度：约 \(O(m \log_2{m})\)。

实际最快用时：799ms，内存：71.66MB（比上面差了很多）。

posted @ 2024-05-02 20:47 Add_Catalyst 阅读(39) 评论(0) 收藏举报

刷新页面返回顶部

珈猫的小窝

欢迎来到珈猫的小窝

P9907 [COCI 2023/2024 #1] Mostovi 题解

P9907 [COCI 2023/2024 #1] Mostovi 题解

前言

题意分析

思路

部分分

正解（大致思路）

代码实现

优化

公告