P5024 保卫王国笔记
神题,神题啊!!(战术后仰)
题意
给定一棵 \(n\) 个节点的树,点有点权。有 \(m\) 个询问,每次询问规定某两个点选或不选,求最小点覆盖。
题解
概念
做题的第一步是:看懂题意。
-
点覆盖:在树上选择某些点,使得对于树上的每一条边,都满足两端点至少有一点被选。
-
最小点覆盖:即选择的点点权和最小的点覆盖。
-
独立集:在树上选择某些点,使得对于树上的每一条边,都满足两端点没有同时被选。
-
最大独立集:即选择的点点权最大的独立集。
不难看出,一棵树上的点覆盖和独立集是一一对应的,一个点覆盖的补集就是一个独立集。所以,最大独立集是最小点覆盖的补集。(虽然这些东西和题意无关,但还是可以扯一下)
思路
先考虑没有询问时,如何求得最小点覆盖?答案是显然的,直接树形 dp 即可,设 \(f_{x, 0 / 1}\) 表示 \(x\) 为根的子树中,\(x\) 选或不选的最小点覆盖权值和,则有:
接着可以发现使用这种 dp,可以用动态 dp 来解决此题。但是这里要讲一种常数较小,代码较短的思想。
由于没有修改,所以不用动态 dp,直接使用倍增即可。考虑倍增所使用的状态 \(h_{u, i, 0 / 1, 0 / 1}\) (设 \(p\) 是 \(u\) 的第 \(2^i\) 级祖先),表示从 \(p\) 的子树中抠掉 \(u\) 这棵子树,第一个 \(0 / 1\) 表示 \(u\) 选还是不选(关于这一维的意义:这里 \(u\) 虽然已经从 \(p\) 中扣掉了,但是在最后回答询问答案时会用到,所以还是要记录一下),第二个表示 \(p\) 选还是不选。
那么有递推式:
然后再考虑新添一个辅助数组 \(g_{x, 0 / 1}\),表示整颗树扣掉了 \(x\) 为根的子树,且 \(x\) 选或不选的答案。于是有(设 \(p\) 为 \(x\) 父亲):
于是在一次询问中,我们可以根据这几个数组求得答案了,具体如下:
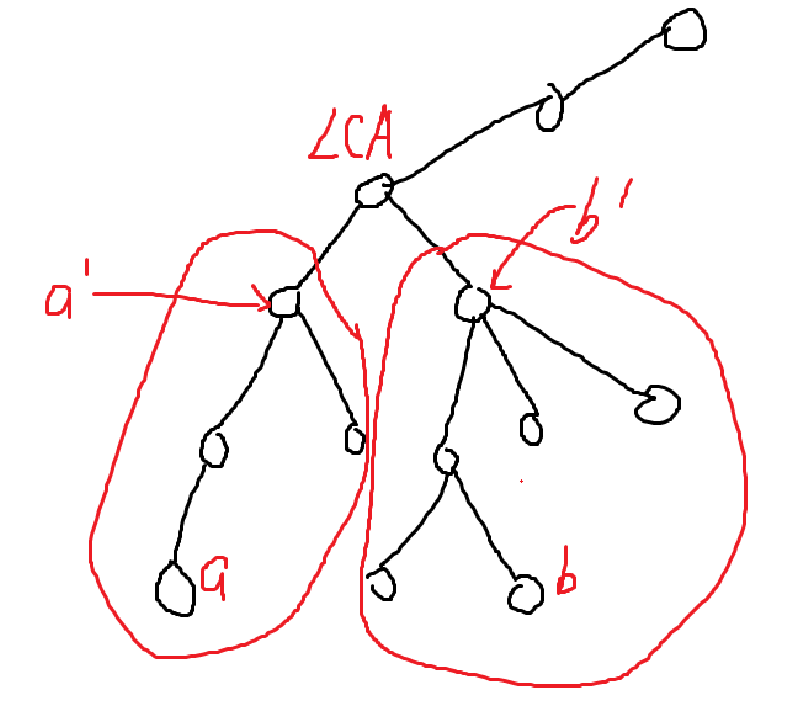
这里给了 \(a, b, x, y\),可以求出 \(a, b\) 的 \(LCA\)。我们可以倍增到 \(LCA\) 的儿子,求出 \(a'\) 与 \(b'\)(如图所示)。假设跳到 \(a', b'\) 的倍增数组分别是 \(A_{0 / 1, 0 / 1}, B_{0 / 1, 0 / 1}\),答案就是以下两种情况的 \(\min\):
不难看出两种情况的区别就是 \(LCA\) 选还是不选。注意这里还要加上 \(LCA\) 的儿子中除了 \(a', b'\) 的其它儿子的贡献(图中未画出)
于是这道题就思路就完了。
代码
用时 ****(数据删除)写的:
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
#define int i64
const int N = 1E5 + 5, M = 20, INF = 1E15;
int n, m, p[N]; vector <int> G[N];
int yf[N][M + 1], dep[N];
i64 f[N][2], h[N][M + 1][2][2], g[N][2];
void dfs(int x, int fa) {
f[x][0] = 0; f[x][1] = p[x];
for (auto v : G[x]) {
if (v == fa) continue;
yf[v][0] = x; dep[v] = dep[x] + 1;
for (int i = 1; i <= M; ++i)
yf[v][i] = yf[yf[v][i - 1]][i - 1];
dfs(v, x);
f[x][0] += f[v][1];
f[x][1] += min(f[v][0], f[v][1]);
}
}
void dfs1(int x, int fa) {
for (auto v : G[x]) {
if (v == fa) continue;
h[v][0][0][0] = INF;
h[v][0][0][1] = f[x][1] - min(f[v][0], f[v][1]);
h[v][0][1][0] = f[x][0] - f[v][1];
h[v][0][1][1] = f[x][1] - min(f[v][0], f[v][1]);
for (int i = 1; i <= M; ++i) {
for (int a : {0, 1}) for (int b : {0, 1}) {
h[v][i][a][b] = INF;
for (int k : {0, 1})
h[v][i][a][b] = min(h[v][i][a][b],
h[v][i - 1][a][k] + h[yf[v][i - 1]][i - 1][k][b]);
}
}
g[v][0] = g[x][1] + f[x][1] - min(f[v][0], f[v][1]);
g[v][1] = min(g[v][0], g[x][0] + f[x][0] - f[v][1]);
dfs1(v, x);
}
}
int solve(int a, int x, int b, int y) {
if (dep[a] < dep[b]) swap(a, b), swap(x, y);
int A[2] = {INF, INF}, B[2] = {INF, INF};
A[x] = f[a][x]; B[y] = f[b][y];
for (int i = M; ~i; --i) {
if (dep[a] - (1 << i) >= dep[b]) {
int pA[] = {A[0], A[1]};
A[0] = min(pA[1] + h[a][i][1][0], pA[0] + h[a][i][0][0]);
A[1] = min(pA[1] + h[a][i][1][1], pA[0] + h[a][i][0][1]);
a = yf[a][i];
}
}
if (a == b) return g[b][y] + A[y];
else {
for (int i = M; ~i; --i) {
if (yf[a][i] != yf[b][i]) {
int pA[] = {A[0], A[1]}, pB[] = {B[0], B[1]};
A[0] = min(pA[1] + h[a][i][1][0], pA[0] + h[a][i][0][0]);
A[1] = min(pA[1] + h[a][i][1][1], pA[0] + h[a][i][0][1]);
B[0] = min(pB[1] + h[b][i][1][0], pB[0] + h[b][i][0][0]);
B[1] = min(pB[1] + h[b][i][1][1], pB[0] + h[b][i][0][1]);
a = yf[a][i]; b = yf[b][i];
}
}
int lca = yf[a][0];
int ans0 = f[lca][0] - f[a][1] - f[b][1] + A[1] + B[1] + g[lca][0];
int ans1 = f[lca][1] - min(f[a][0], f[a][1]) - min(f[b][0], f[b][1]) + min(A[1], A[0]) + min(B[1], B[0]) + g[lca][1];
return min(ans0, ans1);
}
}
signed main(void) {
ios :: sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> m; string typp; cin >> typp; typp = "";
for (int i = 1; i <= n; ++i) cin >> p[i];
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
G[u].emplace_back(v);
G[v].emplace_back(u);
} dep[1] = 1; for (int i = 0; i <= M; ++i) yf[1][i] = 1;
dfs(1, 0); dfs1(1, 0);
map <pair <int, int>, bool> vis;
function <void(int, int)> prep = [&](int x, int fa) {
for (auto v : G[x]) {
if (v == fa) continue;
vis[make_pair(v, x)] = vis[make_pair(x, v)] = 1;
prep(v, x);
}
} ; prep(1, 0);
for (int i = 1; i <= m; ++i) {
int a, x, b, y; cin >> a >> x >> b >> y;
if (!x && !y && vis.count(make_pair(a, b))) {
cout << "-1\n";
continue;
}
cout << solve(a, x, b, y) << '\n';
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号