Codeforces 1702G2 题解

题目大意

给出一个大小为 \(n\) 的树，\(q\) 次询问，每次给出一个大小为 \(m\) 的点集，判断是否有一条链覆盖这些点（这条链可以经过其他点）。

\(n,\sum m\leqslant 2\cdot 10^5\) , \(q\leqslant 10^5\)。

题解

考虑将 \(m\) 个点按树上的深度从大到小排序。

设 \(d_1, d_2\) 分别为链的两端，如果合法，显然链的某一端是排序后第一个节点，这里设 \(d_1\) 为这个节点。因为暂时不知道 \(d_2\) 是谁，于是暂时设 \(d_2 = -1\)。

考虑从前往后遍历这 \(m\) 个点，遍历到一个点 \(x\) 时，可能会出现如下情况：（令 \(\textrm{LCA}(u, v)\) 为 \(u, v\) 的最近公共祖先）

1. \(d_2 \ne -1\land \textrm{LCA}(x, d_1) = x\land \textrm{LCA}(x, d_2) = x\land \textrm{LCA}(d_1, d_2) \ne x\)：此时长成这个样子：
   
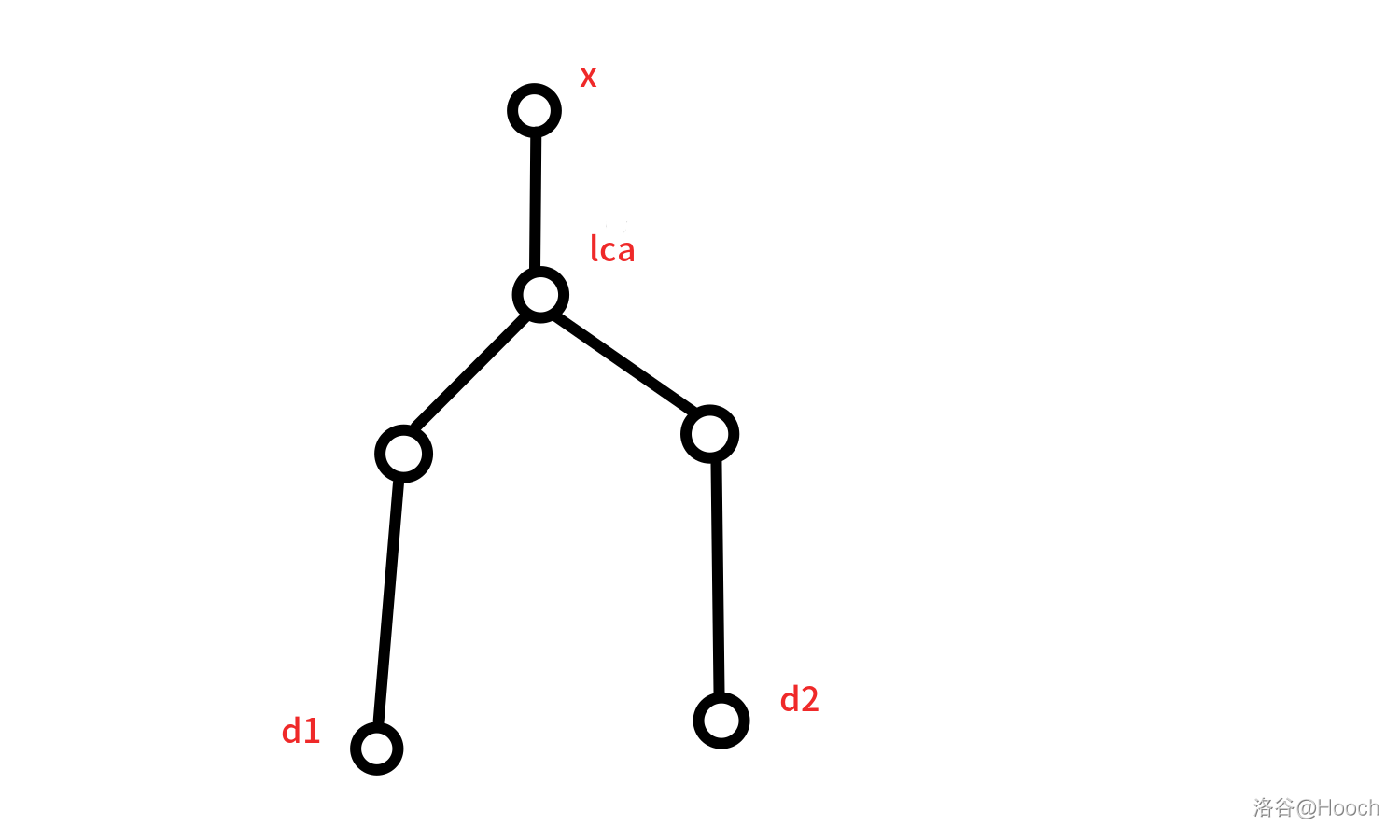
   不合法，直接跳出循环并输出 NO。

2. 如果上述命题不成立，且 \(\textrm{LCA}(d_1, v) = v\)，那么 \(d_1 \gets v\)。

3. 如果上述命题不成立，且 \(d_2\ne -1\land \textrm{LCA}(d_2, v) = v\)，那么 \(d_2 \gets v\)。

4. 如果上述命题不成立，且 \(d_2 = -1\)，那么 \(d_2\gets v\)。

5. 如果上述命题不成立，那么无解。

代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i(0); i < n; ++i)
#define per(i, n) for (int i(n - 1); ~i; --i)
#define Rep(i, j, n) for (int i(j); i <= n; ++i)
#define Per(i, j, n) for (int i(j); i >= n; --i)
#define i64 long long
using namespace std;
namespace FastR {
    const int Bf = 1e5 + 5;
    char buf[Bf], *p1 = buf, *p2 = buf;
    #define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++)
    template <typename T>
    void read(T &x) {
        x = 0; int f = 1; char c = gc();
        while (!isdigit(c)) f -= (c == '-') << 1, c = gc();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c & 15), c = gc();
        x *= f;
    }
    template <typename T, typename ...L>
    void read(T &x, L &...y) {read(x); read(y...);}
    void pt(char c) {putchar(c);}
    template <typename T>
    void write(T x) {
        if (x < 0) pt('-'), x = -x;
        if (x > 9) write(x / 10);
        pt(x % 10 + '0');
    }
}
using namespace FastR;
namespace FastM {
    const int mod = 1e9 + 7;
    int add(i64 x, int y) {
        while (x + y >= mod) return x + y - mod;
        return x + y;
    }
    int des(i64 x, int y) {
        while (x - y < 0) return x - y + mod;
        return x - y;
    }
    int mul(i64 x, int y) {
        while (x * y >= mod) return x * y % mod;
        return x * y;
    }
}
const int N = 2e5 + 5;
int n, q, dep[N], fa[N][25]; vector <int> G[N];
void dfs(int x, int Fa) {
    for (auto v : G[x]) {
        if (v == Fa) continue;
        fa[v][0] = x; dep[v] = dep[x] + 1;
        Rep(i, 1, 20) fa[v][i] = fa[fa[v][i - 1]][i - 1];
        dfs(v, x);
    }
}
int lca(int u, int v) {
    if (dep[u] < dep[v]) swap(u, v);
    Per(i, 20, 0) if (dep[u] - (1 << i) >= dep[v]) u = fa[u][i];
    if (u == v) return u;
    Per(i, 20, 0) 
        if (fa[u][i] != fa[v][i]) { 
            u = fa[u][i];
            v = fa[v][i];
        }
    return fa[u][0];
}
signed main(void) {
    read(n);
    Rep(i, 1, n - 1) {
        int a, b;  read(a, b);
        G[a].emplace_back(b);
        G[b].emplace_back(a);
    } dfs(1, 0);
    read(q); while (q--) {
        int k; read(k);
        vector <int> v;
        Rep(i, 1, k) {int x; read(x); v.emplace_back(x);}
        sort(v.begin(), v.end(), [&](const int &x, const int &y) {return dep[x] > dep[y];});
        int d1 = v[0], d2 = -1, wj = 0;
        Rep(i, 1, (int)v.size() - 1) {
            if (~d2 && lca(d1, v[i]) == v[i] && lca(d2, v[i]) == v[i] && lca(d1, d2) != v[i]) {wj = 1; break;}
            if (lca(d1, v[i]) == v[i]) d1 = v[i];
            else if (~d2 && lca(d2, v[i]) == v[i]) d2 = v[i];
            else if (!~d2) d2 = v[i];
            else {wj = 1; break;}
        }
        printf(wj ? "NO\n" : "YES\n");
    }
}